MBA: Gás simples

Anterior: Por que usar e o que são modelos baseados em indivíduos | Índice: Ecologia | Próximo: MBA: Caminhante aleatório

Colisão entre partículas

Considerando um modelo simples de gás ideal, não há força atuando sob as partículas, então a interação que ocorre entre as partículas se dá apenas por meio de colisões. Assim é necessário calcular a variação na velocidade de cada partícula após a colisão. Começando em uma dimensão, precisamos garantir a conservação do momento: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{1}v_{1}'+m_{2}v_{2}'=m_{1}v_{1}''+m_{2}v_{2}'' } E da energia cinética: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}m_{1}v_{1}'^{2}+\frac{1}{2}m_{2}v_{2}'^{2}=\frac{1}{2}m_{1}v_{1}''^{2}+\frac{1}{2}m_{2}v_{2}''^{2}} Colocando o referencial de forma que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_2'=0} , então as velocidades no novo referencial podem ser escritas como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_i=v_i-v_2'} , de forma que da conservação do momento ficamos com: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''=u_{1}'-\frac{m_{2}}{m_{1}}u_{2}'', \qquad (1) } Elevando ao quadrado: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''^{2}=u_{1}'^{2}-\left(\frac{m_{2}}{m_{1}}\right)^{2}u_{2}''^{2}-2\frac{m_{2}}{m_{1}}u_{1}'u_{2}''} Substituindo na equação de conservação de energia, podemos encontrar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_2''} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} m_{1}u_{1}'^{2}=m_{1}u_{1}''^{2}+m_{2}u_{2}''^{2}\\ m_{1}u_{1}'^{2}=m_{1}\left[u_{1}'{}^{2}+\left(\frac{m_{2}}{m_{1}}\right)^{2}u_{2}''^{2}-2\frac{m_{2}}{m_{1}}u_{1}'u_{2}''\right]+m_{2}u_{2}''^{2}\\ m_{1}u_{1}'^{2}=m_{1}u_{1}'{}^{2}+\frac{m_{2}^{2}}{m_{1}}u_{2}''^{2}-2m_{2}u_{1}'u_{2}''+m_{2}u_{2}''^{2}\\ 0=\left(\frac{m_{2}^{2}}{m_{1}}+m_{2}\right)u_{2}''^{2}+\left(-2m_{2}u_{1}'\right)u_{2}''\\ 0=\left(\frac{m_{2}+m_{1}}{m_{1}}\right)u_{2}''^{2}+\left(-2u_{1}'\right)u_{2}'' \end{array}} Calculando as raízes do segundo grau, temos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{2}''=\frac{2u_{1}'\pm\sqrt{4u_{1}'^{2}}}{2\left(\frac{m_{2}+m_{1}}{m_{1}}\right)}=\frac{m_{1}}{m_{2}+m_{1}}\left(u_{1}'\pm u_{1}'\right)} E como uma solução é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_{2}'=0} , mas queremos a situação em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_{2}'\neq0} , logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'} Substituindo em (1), temos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{1}''=u_{1}'-\frac{m_{2}}{m_{1}}\left(\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'\right)\\ u_{1}''=\left(1-\frac{2m_{2}}{m_{2}+m_{1}}\right)u_{1}\\ u_{1}''=\left(\frac{m_{2}+m_{1}-2m_{2}}{m_{2}+m_{1}}\right)u_{1} \end{array}} Ou seja: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}u_{1}'} Retornando ao referencial original, sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_i=u_i+v_2'} , temos então para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_1'} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}u_{1}'\\ v_{1}''-v_{2}'=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}\left(v_{1}'-v_{2}'\right)\\ v_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}v_{1}'+\left(1-\frac{m_{1}-m_{2}}{m_{2}+m_{1}}\right)v_{2}'\\ v_{1}''=\frac{m_{1}-m_{2}}{m_{2}+m_{1}}v_{1}'+\frac{2m_{2}}{m_{2}+m_{1}}v_{2}' \end{array}} E de maneira análoga para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle v_2'} : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} u_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}u_{1}'\\ v_{2}''-v_{2}'=\frac{2m_{1}}{m_{2}+m_{1}}\left(v_{1}'-v_{2}'\right)\\ v_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}v_{1}'+\left(1-\frac{2m_{1}}{m_{2}+m_{1}}\right)v_{2}'\\ v_{2}''=\frac{2m_{1}}{m_{2}+m_{1}}v_{1}'+\frac{m_{2}-m_{1}}{m_{2}+m_{1}}v_{2}' \end{array}} Um caso especial ocorre se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle m_1=m_2, \qquad (2)} então temos simplesmente: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1''=v_2',\qquad \text{e} \qquad v_2''=v_1'} Em duas dimensões, podemos reduzir o problema a uma dimensão, considerando que toda a alteração na velocidade devido a colisão entre partículas ocorre apenas na componente paralela a reta que liga o centro das duas esferas. Considerando que a posição de cada partícula é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{r}_{i}} , então um vetor entre as partículas pode ser escrito como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}=\overrightarrow{r}_{2}-\overrightarrow{r}_{1}} . Podemos projetar ambas as velocidades então fazendo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {u}_{i}'=\frac{\overrightarrow{v}_{i}\cdot\overrightarrow{d}}{\left|\overrightarrow{d}\right|}=\overrightarrow{v}_{i}\cdot\widehat{d}} Obtemos o módulo da velocidade da partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}} e podemos trabalhar em uma única dimensão para encontrarmos a velocidade de ambas partículas após a colisão nesta dimensão. Ao fim podemos decompor novamente a velocidade final Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle u_i''} em ambos os eixos mantendo a mesma direção utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \theta=\arctan\left(\frac{\Delta{y}}{\Delta x}\right)} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \Delta z = z_2 - z_1} é a diferença entre a posição das partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 2} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1} na componente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle z} .

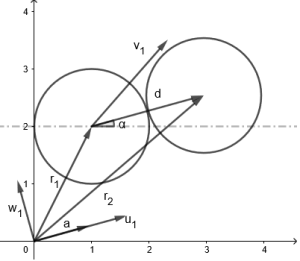
Além disso vale lembrar que há a componente da velocidade perpendicular a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}} , que vamos denotar como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{w}_i=\overrightarrow{v}_i-u_{i}'\left(\cos\theta,\sin\theta\right)} . Esta componente perpendicular permanece inalterada e pode ser visualizada na figura ao lado.

Colisão entre duas partículas mostrando explicitamente os vetores relacionados à partícula 1.

Sendo assim, a velocidade final é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} \overrightarrow{v}_{i}^{\left(f\right)}=\left(u_{i}''\cos\theta,u_{i}''\sin\theta\right)+\overrightarrow{w}_{i}\\ \overrightarrow{v}_{i}^{\left(f\right)}=u_{i}''\left(\cos\theta,\sin\theta\right)+\overrightarrow{v}_{i}-u_{i}'\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\overrightarrow{a} \end{array}} Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{a}} é um vetor unitário que nos dá a direção entre os centros das partículas. Utilizando ad identidades: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\left(\arctan\left(x\right)\right)=\frac{1}{\sqrt{1+x^{2}}}, \qquad \sin\left(\arctan\left(x\right)\right)=\frac{x}{\sqrt{1+x^{2}}}} ficamos então com: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} \overrightarrow{a}=\left(\cos\theta,\sin\theta\right)\\ \overrightarrow{a}=\left(\cos\arctan\left(\frac{\Delta y}{\Delta x}\right),\sin\arctan\left(\frac{\Delta y}{\Delta x}\right)\right)\\ \overrightarrow{a}=\left(\frac{1}{\sqrt{1+\left(\frac{\Delta{y}}{\Delta x}\right)^{2}}},\frac{\left(\frac{\Delta y}{\Delta x}\right)}{\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}}}\right)\\ \overrightarrow{a}=\frac{1}{\Delta x}\frac{1}{\sqrt{1+\left(\frac{\Delta{y}}{\Delta x}\right)^{2}}}\left(\Delta x,\Delta y\right)\\ \overrightarrow{a}=\frac{1}{\frac{\Delta x}{\Delta x}}\frac{1}{\sqrt{\Delta x^{2}+\Delta y^{2}}}\left(\Delta x,\Delta y\right) \end{array}} Logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{a} =\frac{\left(\Delta x,\Delta y\right)}{\sqrt{\Delta x^{2}+\Delta y^{2}}}} E uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{d}=\overrightarrow{r}_{2}-\overrightarrow{r}_{1}=\left(x_{2}-x_{1},y_{2}-y_{1}\right)=\left(\Delta x,\Delta y\right)} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \overrightarrow{a}= \overrightarrow{d}/\left|d\right|= \widehat{d}} . Logo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{v}_{i}^{\left(f\right)}=\overrightarrow{v}_{i}+\left(u_{i}''-u_{i}'\right)\widehat{d}} Ou ainda mais explícito, se fizermos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle m_1=m_2} , sendo as partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle j} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i\neq j} , usando (2): Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{cc} \overrightarrow{v}_{i}^{\left(f\right)} & =\overrightarrow{v}_{i}+\left(u_{j}'-u_{i}'\right)\widehat{d}\\ \overrightarrow{v}_{i}^{\left(f\right)} & =\overrightarrow{v}_{i}+\left(\overrightarrow{v}_{j}\cdot\widehat{d}-\overrightarrow{v}_{i}\cdot\widehat{d}\right)\widehat{d} \end{array}} Temos então que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{v}_{i}^{\left(f\right)} =\overrightarrow{v}_{i}+\left[\left(\overrightarrow{v}_{j}-\overrightarrow{v}_{i}\right)\cdot\widehat{d}\right]\widehat{d}} Todo o cálculo exibido foi para uma partícula, para a segunda partícula, o cálculo é análogo.

Distribuição de velocidades para um gás a certa temperatura

A distribuição das velocidades das moléculas de um gás é dada pela distribuição de Maxwell-Boltzmann

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\left(v\right)=\left(\frac{m}{2\pi kT}\right)^{3/2}4\pi v^{2}\exp\left(-\frac{mv^{2}}{kT}\right) }

Foi realizado uma simulação com 100 partículas por 500.000 de passos em uma grade 100x100 com fronteira toroidal, o resultado encontra-se na figura abaixo assim como o código.

Resultado da simulação com a distribuição de Maxwell-Boltmann para kT=0.7 e m=1.

Código

Aqui chamamos a atenção que a principal diferença do código discutido para autômatos celulares é que agora não temos mais uma grade, mas um modelo contínuo. Também temos a possibilidade de configuração se as fronteiras serão toroidais (extremidades conectadas) ou não. Quanto aos resultados, precisamos considerar que é um modelo simplificado. O Calculo foi realizado para uma colisão entre duas partículas se dentro do mesmo passo deveria ocorrer mais de uma colisão, ou com mais de uma partícula simultaneamente o código falha, para remediar isso, o ideal é utilizar passos de tempo pequenos e/ou uma caixa relativamente grande em relação a quantidade de partículas. Além disso ao optarmos por uma fronteira toroidal ou não, estamos considerando uma caixa fechada ou não, ao considerarmos precisamos considerar a colisão com as fronteira também. Nesse último caso, uma simplificação simples é considerar que esta colisão ocorre primeiro. Novamente o problema surge se houver duas colisões no mesmo passo (agora podendo colidir com a fronteira), logo a recomendação é a mesma.

#Bibliotecas necessárias
from mesa import Agent, Model                                      #Classes Agente e Modelo
from mesa.time import SimultaneousActivation                       #Agendador simultâneo
from mesa.space import ContinuousSpace                             #Malha multigrid
import random                                                      #Número aleatórios
from mesa.datacollection import DataCollector                      #Importamos um coletor de dados
import matplotlib.pyplot as plt                                    #Plotar gráicos             
#from IPython.display import clear_output                           #Configurações de saída do Colab         
import numpy as np    

#AGENTE---------------------------------------------------------------------------------
class Agente(Agent):
    """Classe do agente"""
    def __init__(self, modelo,largura,altura):
        """Bibliotecas necessárias"""
        #modelo     - Modelo que ao qual o agente pertence
        super().__init__(self, modelo)        #Necessário para funcionar o modelo
        self.ppos     = (0,0)                 #Poição que irá se mover
        self.rai= 0.2                         #Raio
        self.lim=(largura,altura)             #Limites da caixa
        v=1                                   #Módulo da velocidade inicial
        ang = 2*random.random()*np.pi
        self.vel      = (v*np.cos(ang),v*np.sin(ang)) #Velocidade decomposta
        self.colisao=False
        self.ac=False
                
    def prox_pos(self):
      dt=0.01
      nx=self.pos[0]+self.vel[0]*0.01
      ny=self.pos[1]+self.vel[1]*0.01
      #Testar os limites
      if (nx < 0):
        nx = - nx; self.vel=(-self.vel[0],self.vel[1])
      if (nx > self.lim[0]):
        nx = 2*self.lim[0] - nx; self.vel=(-self.vel[0],self.vel[1])
      if (ny < 0):
        ny = - ny; self.vel=(self.vel[0], - self.vel[1])
      if (ny > self.lim[1]):
        ny = 2*self.lim[1] - ny;self.vel=(self.vel[0], - self.vel[1])

      return((nx,ny))
    
    def prox_vel(self):
        """Movimentação dos animais"""
        #Checamos se há colisão com outro animal:
        agentes = self.model.continuous.get_neighbors(pos=self.ppos, radius = 3*self.rai, include_center=True)
        for a in agentes:                                         #Percorremos a lista
          if (a.unique_id!=self.unique_id): 
              d=np.sqrt((a.ppos[0]-self.ppos[0])**2+(a.ppos[1]-self.ppos[1])**2)
              if (d<=2*self.rai):
                #Direção da colisão
                d=(a.ppos[0]-self.ppos[0],a.ppos[1]-self.ppos[1])/np.sqrt((a.ppos[0]-self.ppos[0])**2+(a.ppos[1]-self.ppos[1])**2)
                #Partícula 1
                u1=(a.vel[0]-self.vel[0])*d[0]+(a.vel[1]-self.vel[1])*d[1]
                nvel1=(self.vel[0]+u1*d[0],self.vel[1]+u1*d[1])
                #partícula 2,pela conservação de momento:
                nvel2=(self.vel[0]+a.vel[0]-nvel1[0],self.vel[1]+a.vel[1]-nvel1[1])   
                #Se nenhuma partícula tinha se colidido
                if (self.colisao==False and a.colisao==False):          
                  #Atualiza as velocidades
                  self.vel=nvel1; a.vel=nvel2
                  self.ac=True;a.ac=True   
                #Registra a colisão
                self.colisao=True; a.colisao=True       
                break
        return ()                                          

    def movimento(self):
      if(self.colisao):
        return (self.pos)
      else:
        return(self.ppos)
    
    def step(self):
        """Método obrigatório que prepara as mudanças"""
        self.ppos = self.prox_pos()
             
    def advance(self):
        """Método obrigatório que aplica as mudanças"""
        self.prox_vel()
        self.model.continuous.move_agent(self, self.movimento())

#MODELO
class Modelo(Model):
    """Modelo geral"""
    def gerar_particulas(self,N,largura,altura):
      """Função para gerar animais iniciais"""    
      #N        - Número de animais
      #largura  - Largura da grade
      #altura   - Altura da grade
      for n in range(N):
          con=True
          while(con):
            con=False
            a = Agente(self,largura,altura)
            X= largura*random.random()
            Y= altura*random.random()
            if (len(self.schedule.agents)==0):
              self.schedule.add(a)
              self.continuous.place_agent(a, (X, Y))
            else:
              agentes = self.continuous.get_neighbors(pos=(X,Y), radius = 2*a.rai, include_center=True)
              for viz in agentes:
                con = (True) if (len(agentes)==0) else (con)  #Precisamos checar se nasceu no mesmo lugar de outro animal
              if(con==False):
                self.schedule.add(a)
                self.continuous.place_agent(a, (X, Y))
      return()

    def __init__(self, modelo,N,seed=None):
        """Função chamada quando o modelo é inicializazdo"""
        # Modelo   - Dicionário com especificações do modelo
        # N        - Número de partículas
        # seed     - Seed dos números aleatórios do modelo do mesa
        
        # Desempacotar o dicionário
        largura = modelo["Largura"];altura=modelo["Altura"]; random.seed(modelo["Seed"])                     
        self.continuous = ContinuousSpace(x_max= largura, y_max=altura, torus= True, x_min=0, y_min= 0) #Configura a grade
        self.schedule   = SimultaneousActivation(self)            #Configura o agendador
        self.running   = True                                     #Condiçao para seguir executando o modelo
        self.gerar_particulas(N,largura,altura)    #Distribuir as ovelhas
           
    def step(self):
        """Avançar um passo do modelo"""
        self.schedule.step()                              #Avançamos os agentes
        #Limpamos as colisões
        for a in self.schedule.agents:                    #Vamos percorrer os agentes
          a.colisao=False
#Parâmetros
MAX =1000000
N=100
modelo  =  {"Largura":100     ,"Altura":100      ,"Seed":1} 
M = Modelo(modelo,N)
for i in range(MAX):
    M.step()
    if ((i+1)%(MAX/100)==0):
      #clear_output() 
      print(str(100*(1+i)/MAX)+"%")

vel=[]
E=0
for a in M.schedule.agents:
    vel.append(np.sqrt(a.vel[0]**2+a.vel[1]**2))
    E+=a.vel[0]**2+a.vel[1]**2
print(E)
with open('velocidades0.2R100K1000.txt', 'w') as f:
    f.write(str(vel))

Para plotar o gráfico, podemos então usar simplesmente:

import numpy as np
import matplotlib.pyplot as plt

a,b,c=plt.hist(vel,8, density=True, facecolor='g', alpha=0.75)
m=1
K=0.7
x=np.arange(0,2.5, 0.00001)
y = (4/np.sqrt(np.pi))*((m/K)**(3/2))*(x**2)*np.exp(-m*(x**2)/K)
plt.plot(x,y)

Citações

Anterior: Por que usar e o que são modelos baseados em indivíduos | Índice: Ecologia | Próximo: MBA: Caminhante aleatório