Algoritmo de Wang-Landau: mudanças entre as edições
| (18 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 7: | Linha 7: | ||
==Amostragem de Wang-Landau== | ==Amostragem de Wang-Landau== | ||
No início da simulação, <math>g(E)</math> é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir <math>g(E) = 1</math> para todas as energias possíveis <math>E</math>. A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando seu estado. | No início da simulação, <math>g(E)</math> é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir <math>g(E) = 1</math> para todas as energias possíveis <math>E</math>. A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando seu estado (''single-spin flip''). | ||
Cada vez que uma energia <math>E</math> é visitada, o histograma <math>H(E)</math> é incrementado em 1. A estimativa de <math>g(E)</math> é então modificada por um fator multiplicativo <math>f</math>, e o valor atualizado realiza um passeio aleatório adicional no espaço de <math>E</math>. | Cada vez que uma energia <math>E</math> é visitada, o histograma <math>H(E)</math> é incrementado em 1. A estimativa de <math>g(E)</math> é então modificada por um fator multiplicativo <math>f</math>, e o valor atualizado realiza um passeio aleatório adicional no espaço de <math>E</math>. | ||
| Linha 19: | Linha 19: | ||
<math>\frac{p(E_1 \rightarrow E_2)}{p(E_2 \rightarrow E_1)} = \frac{g(E_1)}{g(E_2)}.</math> | <math>\frac{p(E_1 \rightarrow E_2)}{p(E_2 \rightarrow E_1)} = \frac{g(E_1)}{g(E_2)}.</math> | ||
Logo, o algoritmo de passeio aleatório satisfaz o | Logo, o algoritmo de passeio aleatório satisfaz o balanço detalhado no limite em que <math> f \to 1 </math>: | ||
<math>\frac{1}{g(E_1)}p(E_1 \rightarrow E_2) = \frac{1}{g(E_2)}p(E_2 \rightarrow E_1),</math> | <math>\frac{1}{g(E_1)}p(E_1 \rightarrow E_2) = \frac{1}{g(E_2)}p(E_2 \rightarrow E_1),</math> | ||
onde <math>1 / g ( | onde <math>1/g(E_1)</math> é a probabilidade na energia <math>E_1</math> e <math>p (E_1\rightarrow E_2)</math> é a probabilidade de transição de <math>E_1</math> para <math>E_2</math>. | ||
Se o estado de energia <math> E_2 </math> é aceito, a densidade de estados <math> g(E_2) </math> é multiplicada pelo fator de modificação <math> f > 1 </math> de maneira que <math> g(E_2) \to f \times g(E_2) </math> e a entrada no histograma para <math> H(E_2) </math> é atualizada de forma <math> H(E_2) \to H(E_2) + 1 </math>. Se o estado de energia não é aceito, a densidade de estados <math> g(E_1) </math> é multiplicada pelo fator de modificação, <math> g(E_1) \to f \times g(E_1) </math> e <math> H(E_1) </math> é atualizada de forma <math> H(E_1) \to H(E_1) + 1 </math>. | Se o estado de energia <math> E_2 </math> é aceito, a densidade de estados <math> g(E_2) </math> é multiplicada pelo fator de modificação <math> f > 1 </math> de maneira que <math> g(E_2) \to f \times g(E_2) </math> e a entrada no histograma para <math> H(E_2) </math> é atualizada de forma <math> H(E_2) \to H(E_2) + 1 </math>. Se o estado de energia não é aceito, a densidade de estados <math> g(E_1) </math> é multiplicada pelo fator de modificação, <math> g(E_1) \to f \times g(E_1) </math> e <math> H(E_1) </math> é atualizada de forma <math> H(E_1) \to H(E_1) + 1 </math>. | ||
| Linha 29: | Linha 29: | ||
====''Flatness''==== | ====''Flatness''==== | ||
O procedimento de passeio aleatório é seguido até o histograma <math> H(E) </math> estar | O procedimento de passeio aleatório é seguido até o histograma <math> H(E) </math> estar plano (do inglês, "''flat''"), e para determinar isso, a cada <math> n </math> iterações verificamos se todos valores possíveis de <math> E </math> estão a uma distância, no máximo, <math> x% </math> de <math> \langle H(E) \rangle </math>. A variável <math> x </math> é denominada "''flatness''". Quando o histograma está plano, todos estados de energia foram visitados muitas vezes. | ||
O número de passos, < | O número de passos, <math> n </math> que devemos realizar antes de checar deve ser maior que <math> L^2 </math> onde <math> L </math> indica o tamanho da rede, para que o algoritmo tenha a oportunidade de visitar cada estado várias vezes. | ||
Para sistemas simples, podemos utilizar um valor tão alto quanto 95%, entretanto, para este trabalho foi escolhido o valor de 80%. | Para sistemas simples, podemos utilizar um valor tão alto quanto 95%, entretanto, para este trabalho foi escolhido o valor de 80%. | ||
| Linha 39: | Linha 39: | ||
Em geral, como <math> g(E) </math> se torna muito grande, trabalhamos com o logaritmo natural dessas quantidades, <math> \ln g(E) </math>. Portanto, cada atualização da densidade de estados é dada por <math> \ln g(E) \to \ln g(E) + \ln f </math>. O valor comumente utilizado para o fator de modificação é <math> f = f_0 = e </math>. | Em geral, como <math> g(E) </math> se torna muito grande, trabalhamos com o logaritmo natural dessas quantidades, <math> \ln g(E) </math>. Portanto, cada atualização da densidade de estados é dada por <math> \ln g(E) \to \ln g(E) + \ln f </math>. O valor comumente utilizado para o fator de modificação é <math> f = f_0 = e </math>. | ||
Quando o histograma é considerado | Quando o histograma é considerado plano, pelas condições descritas acima, reduzimos o valor de <math> f </math> de forma que o novo valor será <math> f_1 = \sqrt{f_0} </math>, resetamos o histograma <math> H(E) </math> e recomeçamos o passeio aleatório. | ||
A simulação é parada para um valor de <math> f </math> predeterminado. No caso, usamos <math> f_{final} = \exp (10^{-8}) = 1.00000001 </math>. | A simulação é parada para um valor de <math> f </math> predeterminado. No caso, usamos <math> f_{final} = \exp (10^{-8}) = 1.00000001 </math>. | ||
==Aplicação ao Modelo de Ising 2D== | ==Aplicação ao Modelo de Ising 2D== | ||
| Linha 80: | Linha 79: | ||
1. Defino <math>g(E) = 1</math> para todos <math> E </math> e o fator de modificação inicial <math>f_0 = e</math>; | 1. Defino <math>g(E) = 1</math> para todos <math> E </math> e o fator de modificação inicial <math>f_0 = e</math>; | ||
2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade <math> p(E_1 \to E_2) = min(g(E_1)/g(E_2), 1) </math>; | 2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade <math> p(E_1 \to E_2) = \min (g(E_1)/g(E_2), 1) </math>; | ||
3. Modifico a densidade de estados <math> g(E) \to g(E) \times f </math> e atualizo o histograma <math>H(E)</math>; | 3. Modifico a densidade de estados <math> g(E) \to g(E) \times f </math> e atualizo o histograma <math>H(E)</math>; | ||
4. Continuo até o histograma estar | 4. Continuo até o histograma estar plano, então diminuo o valor de <math>f</math>, fazendo <math> f_1 = \sqrt{f_0} </math> e reseto o histograma <math>H(E)</math>; | ||
5. Repito os passos 2-4 até <math> f < 1.00000001 </math>. | 5. Repito os passos 2-4 até <math> f < 1.00000001 </math>. | ||
| Linha 96: | Linha 95: | ||
A estimativa da densidade de estados para <math>L = 16</math> usando a amostragem de Wang-Landau é mostrada na Fig. 1, junto com os resultados exatos de Beale <ref name="beale" />. | A estimativa da densidade de estados para <math>L = 16</math> usando a amostragem de Wang-Landau é mostrada na Fig. 1, junto com os resultados exatos de Beale <ref name="beale" />. | ||
Os fatores de modificação inicial e final para os passeios aleatórios foram <math>ln(f_0) = 1 e ln(f_{final}) = 10^{−8} </math>. | Os fatores de modificação inicial e final para os passeios aleatórios foram <math>ln(f_0) = 1 e \ln(f_{final}) = 10^{−8} </math>. | ||
O histograma <math>H(E)</math> foi considerado plano quando todas as entradas não eram inferiores a 80% da média <math>\langle H(E)\rangle </math>. | O histograma <math>H(E)</math> foi considerado plano quando todas as entradas não eram inferiores a 80% da média <math>\langle H(E)\rangle </math>. | ||
A densidade absoluta de estados na Fig. 1 é obtida pela condição de que o número de estados fundamentais seja 2 para o modelo de Ising 2D. | A densidade absoluta de estados na Fig. 1 é obtida pela condição de que o número de estados fundamentais seja 2 para o modelo de Ising 2D. | ||
Com a escala logarítmica usada na Fig. 1, os dados simulados e a solução exata se sobrepõem perfeitamente. Na inserção da Fig. 1, vemos que o erro relativo é, de fato, muito pequeno. | Com a escala logarítmica usada na Fig. 1, os dados simulados e a solução exata se sobrepõem perfeitamente. Na inserção da Fig. 1, vemos que o erro relativo é, de fato, muito pequeno. | ||
[[Arquivo:Densidade de estado.png| | [[Arquivo:Densidade de estado.png|400px|thumb|center| Figura 1: Logaritmo da densidade de estados <math> \ln g(E) </math> do modelo de Ising 2D com <math> L = 16 </math>.]] | ||
===Distribuição canônica=== | ===Distribuição canônica=== | ||
| Linha 112: | Linha 111: | ||
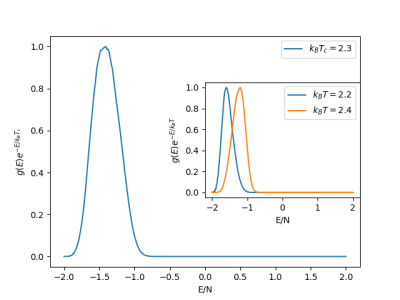
Na Fig. 2, mostramos a distribuição canônica resultante na temperatura crítica <math>T_c</math>, que exibe um único pico. | Na Fig. 2, mostramos a distribuição canônica resultante na temperatura crítica <math>T_c</math>, que exibe um único pico. | ||
[[Arquivo: | [[Arquivo:Newdistcano23.png|400px|thumb|center| Figura 2: Distribuição canônica <math> P(E,T_c) = g(E)e^{-E/k_BT_c} </math> na temperatura de transição do modelo de Ising 2D com <math> L = 16 </math> e <math> k_BT_c = 2.3 </math>.]] | ||
As distribuições em temperaturas acima e abaixo de <math>T_c</math> também apresentam pico único, conforme ilustrado no detalhe da Fig. 3. | As distribuições em temperaturas acima e abaixo de <math>T_c</math> também apresentam pico único, conforme ilustrado no detalhe da Fig. 3. | ||
[[Arquivo:Dists cano.png| | [[Arquivo:Dists cano.png|400px|thumb|center| Figura 3: Distribuição canônica <math> P(E,T) = g(E)e^{-E/k_BT} </math> nas temperaturas <math> T = 2.2 </math> e <math> T = 2.4 </math> do modelo de Ising 2D com <math> L = 16 </math>.]] | ||
===Quantidades termodinâmicas=== | ===Quantidades termodinâmicas=== | ||
| Linha 126: | Linha 124: | ||
Testes mais rigorosos de precisão são fornecidos a partir dos erros relativos para as respectivas quantidades termodinâmicas. Os erros relativos são muito pequenos para toda a região de temperatura de <math>k_BT = 0 - 8</math>. | Testes mais rigorosos de precisão são fornecidos a partir dos erros relativos para as respectivas quantidades termodinâmicas. Os erros relativos são muito pequenos para toda a região de temperatura de <math>k_BT = 0 - 8</math>. | ||
Como o sistema tem uma transição de fase de segunda ordem, a primeira derivada da energia livre é uma função contínua da temperatura. Não há saltos na energia interna ou na entropia, mesmo no limite | Como o sistema tem uma transição de fase de segunda ordem, a primeira derivada da energia livre é uma função contínua da temperatura. Não há saltos na energia interna ou na entropia, mesmo no limite em que o tamanho do sistema vai para o infinito. | ||
tamanho do sistema vai para o infinito. | |||
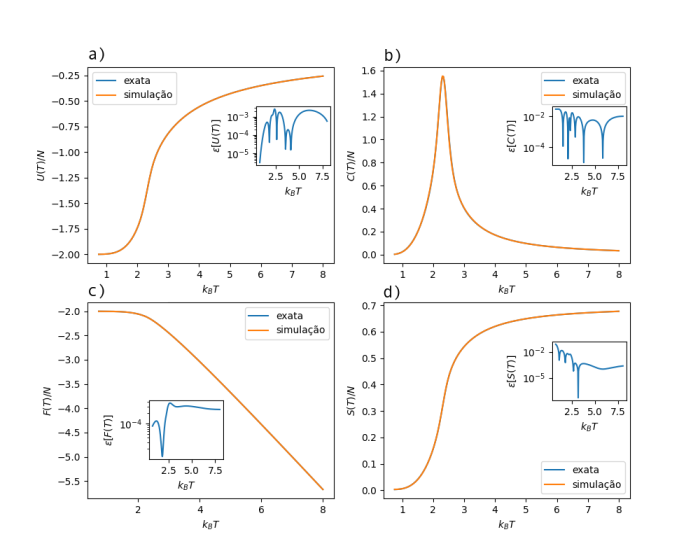
[[Arquivo:Fig33.png|700px|thumb|center| Figura 4: Quantidades termodinâmicas do modelo de Ising 2D com <math> L = 16 </math> calculado a partir da densidade de estados <math> g(E) </math>. Na figura, estão mostrados: (a) energia interna, (b) calor específico, (c) energia livre de Helmholtz e (d) entropia. Os gráficos ''inset'' são os erros relativos.]] | |||
==Magnetização== | |||
Na presença de um campo magnético externo <math>h</math>, o hamiltoniano do modelo de Ising 2D é dado por <math>\mathcal{H} =-\sum_{\langle i,j\rangle} \sigma_i \sigma_j - h \sum_{i=1} \sigma_i</math>, onde <math> M' = \sum_{i=1} \sigma_i </math> é a magnetização e <math>E' =-\sum_{\langle i,j\rangle} \sigma_i \sigma_j </math> é a energia de troca. | |||
A diferença para o algoritmo anterior é que o passeio aleatório agora é executando tanto na energia <math> E' </math> quanto no parâmetro de ordem <math> M' </math>, e um histograma 2D <math> H(E',M') </math> é acumulado. | |||
A função de partição pode ser calculada como <math> Z(T,h)=\sum_{E',M'}g(E',M')e^{-(E'-hM')/k_BT} </math> e, a parir dela, podemos obter quantidades termodinâmicas para todos os valores de temperatura e campo magnético. | |||
Ainda, a magnetização média do sistema é dada por <math> M(T,h) = \frac{\sum_{E',M'}M'g(E',M')e^{-(E'-hM')/k_BT}}{\sum_{E',M'}g(E',M')e^{-(E'-hM')/k_BT}} </math>. | |||
==Conclusões== | |||
O algoritmo de Wang-Landau é uma ferramenta eficiente para o cálculo direto da densidade de estados para grandes sistemas. A alta precisão do método se dá pela modificação da estimativa em cada etapa do passeio aleatório no espaço de energia <math> E </math> e pelo controle cuidadoso do fator de modificação <math> f </math>. | |||
Diferentemente das simulações convencionais de MC, quantidades termodinâmicas como a energia livre de Helmholtz estão diretamente disponíveis uma vez que, usando a densidade de estados, essas quantidades podem ser calculadas essencialmente a qualquer temperatura. | |||
É importante ressaltar que o método de Wang-Landau não está limitado ao passeio aleatório no espaço de energia ou a modelos simples em redes pequenas. Ele pode ser aplicado a qualquer parâmetro e também se mostra eficiente para sistemas grandes, como sistemas complexos gerais com paisagens irregulares. | |||
==Código== | ==Código== | ||
Edição atual tal como às 18h13min de 4 de dezembro de 2021
Nomes: Rafael Abel da Silveira e William Machado Pantaleão
Introdução
Simulações computacionais, como o método de Monte Carlo, são vastamente utilizadas para estudar transições de fase e fenômenos críticos. O método padrão para simulações de Monte Carlo é o algoritmo de Metropolis, entretanto, algoritmos novos e mais eficientes são usados em simulações modernas, como o algoritmo de Wang-Landau. Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica a uma dada temperatura , a abordagem de Wang-Landau estima a densidade de estados diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia . [1]
Mesmo para modelos que podem ser resolvidos analiticamente, a densidade de estados não pode ser determinada para sistemas maiores [2]. Com o algoritmo de Wang-Landau, é possível obter a a partir de um passeio aleatório. A estimativa para é melhorada a cada etapa do passeio aleatório, usando um fator de modificação cuidadosamente controlado, para produzir um resultado que converge para o valor real rapidamente.
Amostragem de Wang-Landau
No início da simulação, é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir para todas as energias possíveis . A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando seu estado (single-spin flip).
Cada vez que uma energia é visitada, o histograma é incrementado em 1. A estimativa de é então modificada por um fator multiplicativo , e o valor atualizado realiza um passeio aleatório adicional no espaço de .
Se e são as energias antes e depois de um valor de spin ser alterado, a probabilidade de transição da energia para é dada por
A razão das probabilidades de transição de para e de a podem ser calculados como
Logo, o algoritmo de passeio aleatório satisfaz o balanço detalhado no limite em que :
onde é a probabilidade na energia e é a probabilidade de transição de para .
Se o estado de energia é aceito, a densidade de estados é multiplicada pelo fator de modificação de maneira que e a entrada no histograma para é atualizada de forma . Se o estado de energia não é aceito, a densidade de estados é multiplicada pelo fator de modificação, e é atualizada de forma .
Flatness
O procedimento de passeio aleatório é seguido até o histograma estar plano (do inglês, "flat"), e para determinar isso, a cada iterações verificamos se todos valores possíveis de estão a uma distância, no máximo, de . A variável é denominada "flatness". Quando o histograma está plano, todos estados de energia foram visitados muitas vezes.
O número de passos, que devemos realizar antes de checar deve ser maior que onde indica o tamanho da rede, para que o algoritmo tenha a oportunidade de visitar cada estado várias vezes.
Para sistemas simples, podemos utilizar um valor tão alto quanto 95%, entretanto, para este trabalho foi escolhido o valor de 80%.
Fator de modificação
Em geral, como se torna muito grande, trabalhamos com o logaritmo natural dessas quantidades, . Portanto, cada atualização da densidade de estados é dada por . O valor comumente utilizado para o fator de modificação é .
Quando o histograma é considerado plano, pelas condições descritas acima, reduzimos o valor de de forma que o novo valor será , resetamos o histograma e recomeçamos o passeio aleatório.
A simulação é parada para um valor de predeterminado. No caso, usamos .
Aplicação ao Modelo de Ising 2D
Modelo de Ising
O modelo de Ising é uma rede 2D, de tamanho que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo[3] Cada sítio pode ter o valor de spin ou .
Para este trabalho, o hamiltoniano de interação pode ser calculado por onde indica pares distintos de vizinhos-mais-próximos.
Com a densidade de estados, podemos calcular as seguintes quantidades termodinâmicas:
Energia interna:
Calor específico:
Energia livre de Helmoltz:
Entropia:
Finalmente, podemos também calcular a distribuição canônica usando:
Algoritmo
Resumindo, o passo a passo do algoritmo pode ser escrito como:
1. Defino para todos e o fator de modificação inicial ;
2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade ;
3. Modifico a densidade de estados e atualizo o histograma ;
4. Continuo até o histograma estar plano, então diminuo o valor de , fazendo e reseto o histograma ;
5. Repito os passos 2-4 até .
6. Obtendo a , posso calcular as quantidades termodinâmicas descritas anteriormente.
Resultados
Densidade de estados
A estimativa da densidade de estados para usando a amostragem de Wang-Landau é mostrada na Fig. 1, junto com os resultados exatos de Beale [2].
Os fatores de modificação inicial e final para os passeios aleatórios foram Falhou ao verificar gramática (erro de sintaxe): {\displaystyle ln(f_0) = 1 e \ln(f_{final}) = 10^{−8} } .
O histograma foi considerado plano quando todas as entradas não eram inferiores a 80% da média .
A densidade absoluta de estados na Fig. 1 é obtida pela condição de que o número de estados fundamentais seja 2 para o modelo de Ising 2D.
Com a escala logarítmica usada na Fig. 1, os dados simulados e a solução exata se sobrepõem perfeitamente. Na inserção da Fig. 1, vemos que o erro relativo é, de fato, muito pequeno.
Distribuição canônica
Podemos calcular a distribuição canônica usando a equação Falhou ao verificar gramática (erro de sintaxe): {\displaystyle P(E, T) = g(E)e^{−E/k_BT}} a qualquer temperatura, sem a necessidade de realizar várias simulações.
Na Fig. 2, mostramos a distribuição canônica resultante na temperatura crítica , que exibe um único pico.
As distribuições em temperaturas acima e abaixo de também apresentam pico único, conforme ilustrado no detalhe da Fig. 3.
Quantidades termodinâmicas
Os resultados simulados, calculados diretamente com as equações descritas no capítulo anterior, e as soluções exatas se sobrepõem quase perfeitamente em uma ampla região de temperatura de .
Testes mais rigorosos de precisão são fornecidos a partir dos erros relativos para as respectivas quantidades termodinâmicas. Os erros relativos são muito pequenos para toda a região de temperatura de .
Como o sistema tem uma transição de fase de segunda ordem, a primeira derivada da energia livre é uma função contínua da temperatura. Não há saltos na energia interna ou na entropia, mesmo no limite em que o tamanho do sistema vai para o infinito.
Magnetização
Na presença de um campo magnético externo , o hamiltoniano do modelo de Ising 2D é dado por , onde é a magnetização e é a energia de troca.
A diferença para o algoritmo anterior é que o passeio aleatório agora é executando tanto na energia quanto no parâmetro de ordem , e um histograma 2D é acumulado.
A função de partição pode ser calculada como e, a parir dela, podemos obter quantidades termodinâmicas para todos os valores de temperatura e campo magnético.
Ainda, a magnetização média do sistema é dada por .
Conclusões
O algoritmo de Wang-Landau é uma ferramenta eficiente para o cálculo direto da densidade de estados para grandes sistemas. A alta precisão do método se dá pela modificação da estimativa em cada etapa do passeio aleatório no espaço de energia e pelo controle cuidadoso do fator de modificação .
Diferentemente das simulações convencionais de MC, quantidades termodinâmicas como a energia livre de Helmholtz estão diretamente disponíveis uma vez que, usando a densidade de estados, essas quantidades podem ser calculadas essencialmente a qualquer temperatura.
É importante ressaltar que o método de Wang-Landau não está limitado ao passeio aleatório no espaço de energia ou a modelos simples em redes pequenas. Ele pode ser aplicado a qualquer parâmetro e também se mostra eficiente para sistemas grandes, como sistemas complexos gerais com paisagens irregulares.
Código
from scipy import *
import sys
import numpy as np
from pylab import *
from matplotlib import pyplot as plt
#Rede aleatória para Ising 2D
def redeAleatoria(L):
latt=zeros((L,L),dtype=int)
for i in range(L):
for j in range(L):
latt[i,j]=sign(2*rand()-1)
return latt
#Energia da rede
def energia(latt):
Ene=0
for i in range(L):
for j in range(L):
S=latt[i,j]
WF=latt[(i+1)%L,j]+latt[i,(j+1)%L]+latt[(i-1)%L,j]+latt[i,(j-1)%L]
Ene+=-WF*S
return int(Ene/2.)
#Quantidades termodinâmicas usando a densidade de estados
def quantTermod(T,lngE,Energies,E0):
Z=0
Ev=0
E2v=0
for i,E in enumerate(Energies):
w=exp(lngE[i]-E/T)
Z+=w
Ev+=w*E
E2v+=w*E**2
Ev*=1./Z
cv=(E2v/Z-Ev**2)/T**2
F = -T*np.log(Z)
S = (Ev - F)/T
return (Ev/N,cv/N,F/N,S/N)
#Algoritmo de Wang-Landau
def WangLandau(L,N,indices,E0,flatness,fmin):
latt=redeAleatoria(L)
Ene=energia(latt)
lngE=zeros(len(Energies),dtype=float)
Hist=zeros(len(Energies),dtype=float)
lnf=1.0
itt = 0
while exp(lnf) > fmin:
itt = itt + 1
ii=int(rand()*N)
(i,j)=(ii%L,ii/L)
i=int(rand()*L)
j=int(rand()*L)
S=latt[i,j]
WF=latt[(i+1)%L,j]+latt[i,(j+1)%L]+latt[(i-1)%L,j]+latt[i,(j-1)%L]
Enew=Ene+2*S*WF
P=exp(lngE[indices[Ene+E0]]-lngE[indices[Enew+E0]])
if P>rand():
latt[i,j]=-S
Ene=Enew
Hist[indices[Ene+E0]]+=1.
lngE[indices[Ene+E0]]+=lnf
if itt%1000==0:
aH=sum(Hist)/(N)
mH=min(Hist)
if mH>aH*flatness:
Hist=zeros(len(Hist))
lnf/=2.
print("iteracao =", itt, 'f=', exp(lnf))
return lngE,Hist
fmin = 1.00000001
print(fmin)
L=16
flatness=0.8
N=L*L
# energias possiveis
Energies = (4*arange(N+1)-2*N).tolist()
print(Energies)
Energies.pop(1)
Energies.pop(-2)
E0=Energies[-1]
print(Energies)
indices=-ones(E0*2+1,dtype=int)
for i,E in enumerate(Energies):
indices[E+E0]=i
(lngE, Hist) = WangLandau(L, N, indices, E0, flatness, fmin)
Hist *= len(Hist)/sum(Hist)
len(lngE),len(Hist)
from pylab import *
EE=array(Energies);EE=EE/(L*L)
plt.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
#plt.plot(EE,Hist,'-s',markersize=2.0,label='Histogram')
xlabel(r'$E/N$')
ylabel(r'$ln[g(E)]$')
legend(loc='best')
show()
f=open('bealeL16.dat','r');f=f.readlines()
beale=[]
for i in range(len(f)):
beale.append(float(f[i]))
plt.plot(Energies,beale,label='Exata')
xlabel('Energia')
ylabel('ln[g(E)]')
legend(loc='best')
show()
plt.plot(EE,beale,label='Exata')
plt.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
xlabel(r'$E/N$')
ylabel(r'$ln[g(E)]$')
legend(loc='best')
show()
#Erro relativo
erro=[]
for i in range(len(lngE)):
erro.append((abs(lngE[i]-beale[i]))/beale[i])
plt.plot(Energies,erro)
xlabel('Energia')
ylabel(r'$\epsilon [ln(g)]$')
#legend(loc='best')
yscale('log')
show()
from mpl_toolkits.axes_grid.inset_locator import (inset_axes,InsetPosition,mark_inset)
fig,ax1=subplots()
ax1.plot(EE,lngE,'o',markersize=1.5,label='Simulação')
ax1.plot(EE,beale,label='Exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$ln[g(E)]$')
ax1.set_xlim(-2.,4.)
ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.685,0.5,0.3,0.3])
ax2.set_axes_locator(ip)
ax2.plot(EE,erro)
ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$\epsilon [ln(g)]$')
savefig('fig1.png')
show()
print(beale[0:5])
print(lngE[0:5])
lmb23 = -1**300
lmb23e = -1**300
i=0
while i<N-1:
termo23 = lngE[i] - Energies[i]/2.3
if termo23 > lmb23:
lmb23 = termo23
i = i+1
i=0
while i<N-1:
termo23e = beale[i] - Energies[i]/2.3
if termo23e > lmb23e:
lmb23e = termo23e
i = i+1
print(lmb23,lmb23e)
lmb22 = -1**300
lmb22e = -1**300
lmb24 = -1**300
lmb24e = -1**300
i=0
while i<N-1:
termo22 = lngE[i] - Energies[i]/2.2
if termo22 > lmb22:
lmb22 = termo22
i = i+1
i=0
while i<N-1:
termo22e = beale[i] - Energies[i]/2.2
if termo22e > lmb22e:
lmb22e = termo22e
i = i+1
i=0
while i<N-1:
termo24 = lngE[i] - Energies[i]/2.4
if termo24 > lmb24:
lmb24 = termo24
i = i+1
i=0
while i<N-1:
termo24e = beale[i] - Energies[i]/2.4
if termo24e > lmb24e:
lmb24e = termo24e
i = i+1
print(lmb22,lmb22e,lmb24,lmb24e)
E=array(Energies);E1=E/N
P=exp(lngE-E/2.3 - lmb23)
Pexact=exp(beale-E/2.3 - lmb23e)
plt.plot(E1,P,label=r'$k_B T_c = 2.3$')
plt.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
#plt.plot(Energies,P2,label=r'$k_B T_c = 2.2$')
#plt.plot(Energies,P3,label=r'$k_B T_c = 2.4$')
xlabel('E/N')
ylabel(r'$g(E)e^{-E/k_B T_c}$')
legend(loc='best')
show()
P2=exp(lngE-E/2.2-lmb22)
P2exact=exp(beale-E/2.2-lmb22e)
P3=exp(lngE-E/2.4-lmb24)
P3exact=exp(beale-E/2.4-lmb24e)
fig,ax1=subplots()
ax1.plot(E1,P,label=r'$k_B T_c = 2.3$')
#ax1.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$g(E)e^{-E/k_B T_c}$')
#ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.5,0.3,0.5,0.5])
ax2.set_axes_locator(ip)
ax2.plot(E1,P2,label=r'$k_B T = 2.2$')
#ax2.plot(E1,P2exact,label=r'$k_B T = 2.2$ exata')
ax2.plot(E1,P3,label=r'$k_B T = 2.4$')
#ax2.plot(E1,P3exact,label=r'$k_B T = 2.4$ exata')
#ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$g(E)e^{-E/k_B T}$')
ax2.legend(loc='best')
savefig('fig2.png')
show()
E=array(Energies);E1=E/N
P=exp(lngE-E/2.3 - lmb23)
Pexact=exp(beale-E/2.3 - lmb23e)
plt.plot(E1,P,label=r'$k_B T_c = 2.3$')
plt.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
#plt.plot(Energies,P2,label=r'$k_B T_c = 2.2$')
#plt.plot(Energies,P3,label=r'$k_B T_c = 2.4$')
xlabel('E/N')
ylabel(r'$g(E)e^{-E/k_B T_c}$')
legend(loc='best')
show()
lmb22 = -1**300
lmb22e = -1**300
lmb24 = -1**300
lmb24e = -1**300
i=0
while i<N-1:
termo22 = lngE[i] - Energies[i]/2.2
if termo22 > lmb22:
lmb22 = termo22
i = i+1
i=0
while i<N-1:
termo22e = beale[i] - Energies[i]/2.2
if termo22e > lmb22e:
lmb22e = termo22e
i = i+1
i=0
while i<N-1:
termo24 = lngE[i] - Energies[i]/2.4
if termo24 > lmb24:
lmb24 = termo24
i = i+1
i=0
while i<N-1:
termo24e = beale[i] - Energies[i]/2.4
if termo24e > lmb24e:
lmb24e = termo24e
i = i+1
print(lmb22,lmb22e,lmb24,lmb24e)
P2=exp(lngE-E/2.2-lmb22)
P2exact=exp(beale-E/2.2-lmb22e)
P3=exp(lngE-E/2.4-lmb24)
P3exact=exp(beale-E/2.4-lmb24e)
fig,ax1=subplots()
ax1.plot(E1,P,label=r'$k_B T_c = 2.3$')
#ax1.plot(E1,Pexact,label=r'$k_B T_c = 2.3$ exata')
ax1.set_xlabel('E/N')
ax1.set_ylabel(r'$g(E)e^{-E/k_B T_c}$')
#ax1.set_ylim(0.,200.)
ax1.legend(loc='best')
ax2=axes([0,0,1,1])
ip=InsetPosition(ax1,[0.5,0.3,0.5,0.5])
ax2.set_axes_locator(ip)
ax2.plot(E1,P2,label=r'$k_B T = 2.2$')
#ax2.plot(E1,P2exact,label=r'$k_B T = 2.2$ exata')
ax2.plot(E1,P3,label=r'$k_B T = 2.4$')
#ax2.plot(E1,P3exact,label=r'$k_B T = 2.4$ exata')
#ax2.set_yscale('log')
ax2.set_xlabel('E/N')
ax2.set_ylabel(r'$g(E)e^{-E/k_B T}$')
ax2.legend(loc='best')
savefig('fig2.png')
show()
Te = linspace(0,8,255)
Thm=[];Thm_exact=[]
for T in Te:
Thm.append(quantTermod(T, lngE, Energies, E0))
Thm_exact.append(quantTermod(T, beale, Energies, E0))
Thm = array(Thm)
Thm_exact=array(Thm_exact)
#Energia interna
plt.plot(Te,Thm_exact[:,0],label='exata')
plt.plot(Te,Thm[:,0],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$U(T)/N$')
plt.legend(loc='best')
plt.show()
#Calor específico
plt.plot(Te,Thm_exact[:,1],label='exata')
plt.plot(Te,Thm[:,1],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$C(T)/N$')
plt.legend(loc='best')
plt.show()
#Energia livre de Helmholtz
plt.plot(Te,Thm_exact[:,2],label='exata')
plt.plot(Te,Thm[:,2],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$F(T)/N$')
plt.legend(loc='best')
plt.show()
#Entropia
plt.plot(Te,Thm_exact[:,3],label='exata')
plt.plot(Te,Thm[:,3],label='simulação')
plt.xlabel(r'$k_B T$')
plt.ylabel(r'$S(T)/N$')
plt.legend(loc='best')
plt.show()
erroUt=(abs(Thm[:,0]-Thm_exact[:,0]))/abs(Thm_exact[:,0])
erroCt=(abs(Thm[:,1]-Thm_exact[:,1]))/Thm_exact[:,1]
erroFt=(abs(Thm[:,2]-Thm_exact[:,2]))/abs(Thm_exact[:,2])
erroSt=(abs(Thm[:,3]-Thm_exact[:,3]))/Thm_exact[:,3]
#Erro relativo para energia interna
plt.plot(Te,erroUt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [U(T)]$')
yscale('log')
plt.show()
#Erro relativo para calor específico
plt.plot(Te,erroCt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [C(T)]$')
yscale('log')
plt.show()
#Erro relativo para energia livre de Helmholtz
plt.plot(Te,erroFt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [F(T)]$')
yscale('log')
plt.show()
#Erro relativo para entropia
plt.plot(Te,erroSt)
xlabel(r'$k_B T$')
ylabel(r'$\epsilon [S(T)]$')
yscale('log')
plt.show()
figure(figsize=(10,8))
ax1=subplot(2,2,1)
ax1.plot(Te,Thm_exact[:,0],label='exata')
ax1.plot(Te,Thm[:,0],label='simulação')
ax1.set_xlabel(r'$k_B T$')
ax1.set_ylabel(r'$U(T)/N$')
ax1.legend(loc='best')
ax12=axes([1,0,0,0])
ip=InsetPosition(ax1,[0.685,0.5,0.3,0.3])
ax12.set_axes_locator(ip)
ax12.plot(Te,erroUt)
ax12.set_yscale('log')
ax12.set_xlabel(r'$k_B T$')
ax12.set_ylabel(r'$\epsilon [U(T)]$')
ax2=subplot(2,2,2)
ax2.plot(Te,Thm_exact[:,1],label='exata')
ax2.plot(Te,Thm[:,1],label='simulação')
ax2.set_xlabel(r'$k_B T$')
ax2.set_ylabel(r'$C(T)/N$')
ax2.legend(loc='best')
ax22=axes([0,1,0,0])
ip=InsetPosition(ax2,[0.685,0.5,0.3,0.3])
ax22.set_axes_locator(ip)
ax22.plot(Te,erroCt)
ax22.set_yscale('log')
ax22.set_xlabel(r'$k_B T$')
ax22.set_ylabel(r'$\epsilon [C(T)]$')
ax3=subplot(2,2,3)
ax3.plot(Te,Thm_exact[:,2],label='exata')
ax3.plot(Te,Thm[:,2],label='simulação')
ax3.set_xlabel(r'$k_B T$')
ax3.set_ylabel(r'$F(T)/N$')
ax3.legend(loc='best')
ax32=axes([0,0,1,0])
ip=InsetPosition(ax3,[0.25,0.2,0.3,0.3])
ax32.set_axes_locator(ip)
ax32.plot(Te,erroFt)
ax32.set_yscale('log')
ax32.set_xlabel(r'$k_B T$')
ax32.set_ylabel(r'$\epsilon [F(T)]$')
ax4=subplot(2,2,4)
ax4.plot(Te,Thm_exact[:,3],label='exata')
ax4.plot(Te,Thm[:,3],label='simulação')
ax4.set_xlabel(r'$k_B T$')
ax4.set_ylabel(r'$S(T)/N$')
ax4.legend(loc='best')
ax42=axes([0,0,0,1])
ip=InsetPosition(ax4,[0.685,0.5,0.3,0.3])
ax42.set_axes_locator(ip)
ax42.plot(Te,erroSt)
ax42.set_yscale('log')
ax42.set_xlabel(r'$k_B T$')
ax42.set_ylabel(r'$\epsilon [S(T)]$')
savefig('fig3.png')
show()
Referências
<references>
- ↑ D. P. Landau, Shan-ho Tsai, M. Exler, A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling, American Journal of Physics 72, 1294 (2004). https://doi.org/10.1119/1.1707017
- ↑ 2,0 2,1 P. D. Beale, Exact Distribution of Energies in the Two-Dimensional Ising Model, Phys. Rev. Lett. 76,78 (1996). https://doi.org/10.1103/PhysRevLett.76.78
- ↑ A. Rosa, C. Pires, L. Doria, Ising 2D, Wiki da Física Computacional da UFRGS. https://fiscomp.if.ufrgs.br/index.php/Ising_2D#Modelo_de_Ising