Equação de Cahn-Hilliard: mudanças entre as edições
| (161 revisões intermediárias por 4 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David | '''Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss''' | ||
O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard, que descreve o processo de decomposição | O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard, que descreve o processo de decomposição espinodal de uma mistura binária, e analisar como é seu comportamento com diferentes coeficientes de difusão, utilizando o método FTCS (''Forward Time Centered Space''). O trabalho foi inspirado no artigo de Sibbing[1]. | ||
== Decomposição Espinodal == | == Decomposição Espinodal == | ||
Decomposição espinodal é o nome dado ao processo no qual uma pequena perturbação de um sistema faz com que | Decomposição espinodal é o nome dado ao processo no qual uma pequena perturbação de um sistema faz com que uma fase homogênea termodinamicamente instável diminua sua energia e separe-se espontaneamente em duas outras fases coexistentes, esse é um processo que ocorre sem nucleação, ou seja, é instantâneo. Ela é observada, por exemplo, em misturas de metais ou polímeros [2]. | ||
==A Equação de Cahn-Hilliard== | ==A Equação de Cahn-Hilliard== | ||
A equação de Cahn-Hilliard | A equação de Cahn-Hilliard é uma equação que descreve o processo de separação de fase entre dois componentes de um fluido binário que se separam de maneira espontânea. | ||
Com o intuito de deduzirmos essa equação, consideraremos - de início - uma mistura binária de dois componentes A e B descritas pelas concentrações dos fluidos <math> c_a(x,t) </math> e <math> c_b(x,t) </math>, respectivamente. [1] | |||
Além disso, podemos considerar que - para uma mistura binária - <math> c_a(x,t) + c_b(x,t) = 1</math> e portanto podemos simplificar para apenas uma concentração <math> c(x,t) </math>: | Além disso, podemos considerar que - para uma mistura binária - <math> c_a(x,t) + c_b(x,t) = 1</math> e portanto podemos simplificar para apenas uma concentração <math> c(x,t) </math>: | ||
:<math> | :<math> | ||
c_a(x,t) = c(x,t), c_b(x,t) = 1 - c(x,t) | c_a(x,t) = c(x,t), c_b(x,t) = 1 - c(x,t). | ||
</math> | </math> | ||
| Linha 23: | Linha 21: | ||
J = -D\nabla c | J = -D\nabla c | ||
</math> | </math> | ||
juntamente da equação da continuidade: | |||
:<math> | :<math> | ||
\frac{\partial c}{\partial t} + \nabla \cdot \vec J = 0. | |||
</math> | </math> | ||
Onde <math>D</math> é | Onde <math>D</math> é o coeficiente de difusão e <math>\vec J</math> é o fluxo de difusão de concentração da mistura. Em seguida, ao combinarmos ambas as equações anteriores o resultado gera a segunda lei de Fick da difusão: | ||
Em seguida, ao | |||
:<math> | :<math> | ||
\frac{\partial c}{\partial t} = D {\nabla}^2 c. | |||
</math> | </math> | ||
A partir dessa equação - como não há a existência de um gradiente de concentração espacial - pode-se esperar que não ocorra mudança na concentração da mistura. No entanto, observa-se que quando a separação de fases ocorre, a difusão demonstra ser contrária ao gradiente de concentração, o que não condiz com a equação anterior. | |||
Tendo isso em vista, conclui-se que a concentração não pode ser a razão da difusão, portanto outra força deve estar presente. E, nesse caso, encontrou-se que a principal força responsável pela difusão negativa (difusão que "o estado de equilíbrio é um sistema de duas fases separadas por uma interface", seção 1.1 de [1]) é o potencial químico (de acordo com Cahn e Hilliard, 1958). Portanto, outra equação pode ser derivada para generalizar a primeira lei de Fick: | |||
:<math> | :<math> | ||
J = - | J = -M \nabla \mu. | ||
</math> | </math> | ||
Onde <math>M</math> é a mobilidade das partículas (análoga à D) e <math>\mu</math> é o potencial químico. | |||
Com essa nova equação podemos agora também deduzir uma nova equação para a segunda lei de Fick [3]: | |||
:<math> | :<math> | ||
\frac{\partial c | \frac{\partial c}{\partial t} = M {\nabla}^2 \mu. | ||
</math> | </math> | ||
Nessa equação, podemos usar a definição do potencial químico através da densidade da energia livre de Gibbs como: | |||
:<math> | :<math> | ||
\frac{\partial | \mu = \frac{\partial g}{\partial c}. | ||
</math> | </math> | ||
Onde <math>g</math> é a densidade da energia livre de Gibbs e <math>c</math> é a concentração (de acordo com Schroeder, 1999). | |||
Tendo em vista a substituição do termo <math>\mu</math> por um termo que envolva a concentração dos fluidos, utiliza-se uma equação que descreve a densidade de energia desse sistema através da concentração dos mesmos (derivado em [3]): | |||
:<math> | :<math> | ||
G = \int_{V}^{} f(c) + {\kappa |\nabla c|}^2 dV. | |||
</math> | </math> | ||
Nesse caso, <math>G</math> é a energia livre de Gibbs, <math>f(c)</math> é a densidade de energia livre devido à contribuições de ambas as fases homogêneas e <math>{\kappa|\nabla c|}^2</math> é a densidade de energia livre devido ao gradiente de concentração. | |||
Além disso, a função <math>f(c)</math> - de acordo com [8] - possui o potencial de um poço de potencial duplo. Neste poço, <math>c</math> representa a concentração em escala e está relacionada à temperatura da mistura, que decide se a separação de fases irá - ou não - ocorrer. Esta função pode ser representada pela seguinte equação: | |||
:<math> | :<math> | ||
f(c) = \frac{(c^2 - 1)^2}{4} | f(c) = \frac{(c^2 - 1)^2}{4}. | ||
</math> | |||
Levando essas informações em conta e - utilizando um parâmetro <math>\gamma</math> análogo à largura da interface - que é descrito por <math>\kappa = \gamma ^2</math> é possível encontrar uma equação que descreve a densidade de energia livre de Gibbs para um sistema com duas fases. | |||
:<math> | |||
g(c) = f(c) + {\gamma}^2{|\nabla c |}^2. | |||
</math> | |||
Com essas igualdades agora se torna possível o cálculo de <math>\mu</math> em função da concentração dos fluidos: | |||
:<math> | |||
\mu = \frac{\partial g}{\partial c} = \frac{\partial f(c)}{\partial c} + \frac{\partial }{\partial c} (\gamma^2{|\nabla c |}^2) = \frac{\partial }{\partial c} \frac{(c^2 - 1)^2}{4} + {\gamma}^2 {\nabla}^2 c = c^3 - c + {\gamma}^2 {\nabla}^2 c. | |||
</math> | |||
Finalmente - utilizando a última expressão encontrada - torna-se possível reescrever o potencial químico em função da mobilidade de suas partículas (<math>M</math>) e a concentração do fluido: | |||
:<math> | |||
\frac{\partial c}{\partial t} = M {\nabla}^2 (c^3 - c - \gamma {\nabla}^2 c). | |||
</math> | |||
Essa equação final é chamada de equação de Cahn-Hilliard. | |||
A equação dependente da difusão é análoga e também funcional e pode ser escrita em relação ao potencial químico: | |||
:<math> | |||
\frac{\partial c}{\partial t} = D {\nabla}^2 (c^3 - c - \gamma {\nabla}^2 c) = D {\nabla}^2 u. | |||
</math> | </math> | ||
== Método FTCS (Forward Time Centered Space) == | == Método FTCS (Forward Time Centered Space) == | ||
O FTCS é um método numérico utilizado para resolver equações diferenciais parciais, tais como a difusão do calor e do transporte de massa, traduzindo, significa "Progressivo no tempo, | O FTCS é um método numérico utilizado para resolver equações diferenciais parciais, tais como a difusão do calor e do transporte de massa, traduzindo, significa "Progressivo no tempo, centrado no espaço". Uma das formas que o método pode ser utilizado é a forma explícita que está descrita abaixo. | ||
:<math>n\to\Delta t</math> | :<math>n\to\Delta t</math> | ||
| Linha 77: | Linha 110: | ||
:<math>f_j^{n+1}= f_j^{n} + \frac{D\Delta t}{(\Delta x)^2} (f_{j-1}^{n} - 2f_j^{n} + f_{j+1}^{n})</math> | :<math>f_j^{n+1}= f_j^{n} + \frac{D\Delta t}{(\Delta x)^2} (f_{j-1}^{n} - 2f_j^{n} + f_{j+1}^{n})</math> | ||
=== FTCS | == Implementação da equação de Cahn-Hilliard 1D pelo método FTCS explícito == | ||
:<math>\displaystyle \frac{\partial c}{\partial t} = D\nabla^{2}(c^{3}-c-\gamma^2\nabla^{2}c)</math> | |||
:<math>\displaystyle \frac{c_{j}^{n+1}-c_{j}^{n}}{\Delta t} = D\displaystyle \frac{\partial ^2 }{\partial x^2}(c^3 - c - \gamma^2 \displaystyle \frac{\partial ^2 c}{\partial x^2})</math> | |||
substituindo <math>(c^{3}-c-\gamma^2\nabla^{2}c)</math> por <math>\mu</math> (potencial químico) | |||
:<math>\displaystyle \frac{c_{j}^{n+1}-c_{j}^{n}}{\Delta t} = D\frac{\mu _{j-1}^n-2\mu _j^n + \mu _{j+1}^n}{(\Delta x)^2}</math> | |||
:<math>\displaystyle \frac{c_{j}^{n+1}-c_{j}^{n}}{\Delta t} = D\left(\frac{(c_{j-1}^n)^3-2(c_j^n)^3 + (c_{j+1}^n)^3}{(\Delta x)^2} - \frac{c_{j-1}^n-2 c_i^n + c_{j+1}^n}{(\Delta x)^2} - \gamma^2\frac{c_{j-2}^n-4c_{j-1}^n + 6c_{j}^n -4c_{j+1}^n + c_{j+2}^n}{(\Delta x)^4}\right)</math> | |||
:<math> c_{j}^{n+1} = D\Delta t \left (\frac{(c_{j-1}^n)^3-2(c_i^n)^3 + (c_{j+1}^n)^3}{(\Delta x)^2} - \frac{c_{j-1}^n-2 c_j^n + c_{j+1}^n}{(\Delta x)^2} - \gamma^2\frac{c_{j-2}^n-4c_{j-1}^n + 6c_{j}^n -4c_{j+1}^n + c_{j+2}^n}{(\Delta x)^4} \right) + c_j^n</math> | |||
:<math>c_{j}^{n+1} = \frac{D\Delta t}{(\Delta x)^2} \left ((c_{j-1}^n)^3-2(c_i^n)^3 + (c_{j+1}^n)^3 - {c_{j-1}^n+2 c_j^n - c_{j+1}^n} - \gamma^2\frac{c_{j-2}^n-4c_{j-1}^n + 6c_{j}^n -4c_{j+1}^n + c_{j+2}^n}{(\Delta x)^2} \right) + c_j^n </math> | |||
'''Condição de Estabilidade ''' | |||
A estabilidade dessa equação mostra-se muito mais complicada de se estipular por ela ser uma equação diferencial de quarta ordem se comparada a equação de difusão, Portanto só iremos analisar a seção 3.3 (Experimental and theoretical stability conditions) do artigo Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions [1]. | |||
Após a linearização e aplicação do teorema de Gershgorin temos que a condição para estabilidade da equação linear para <math>D = 1</math> é: | |||
:<center><math>\Delta t < \displaystyle\frac{(\Delta x)^2}{4+\frac{8\gamma^2}{\Delta x^2}}</math> | |||
Importante atentar que essa é a condição de estabilidade somente para a equação de Cahn-Hilliard linearizada, não para a original. Tanto que a literatura sobre a equação propõem que <math>\Delta t</math> <math>\varpropto</math> <math>(\Delta x)^4 </math>, que é o que acontece na condição estabilidade linear quando <math>\gamma >> \Delta x</math>. | |||
O artigo compara os dados experimentais de estabilidade com a estabilidade da equação linearizada relacionado na seção 3.3.4 e conclui que para valores de <math>\frac{\gamma}{\Delta x} \in [0.25,8]</math> a condição teórica encontrada a partir da linearização é uma boa aproximação. | |||
'''Condição de Contorno''' | |||
Foram utilizadas duas condições de contorno para produzir os resultados, o gráfico 1 foi criado estabelecendo que: | |||
<math> | |||
c(0,t)= 1 ; c(L,t)= 1 | |||
</math> | |||
Onde L é o comprimento da grid, essa condição de Dirichlet adiciona matéria ao problema, mas é uma forma prática de analisar diferentes coeficientes de difusão. Para os demais resultados foram utilizadas condições de contorno periódicas. | |||
'''Condições Iniciais ''' | |||
Para os resultados do gráfico 1 e 2 foram utilizadas como condições iniciais a concentração -1 para a primeira metade de L e 1 para a segunda metade: | |||
<math> | |||
c(x,t=0)=\left\{\begin{array}{lc} -1,\quad 0 \le x \le \frac{1}{2}L \\ | |||
1, \quad \frac{1}{2}L < x \le L \end{array}\right. | |||
</math> | |||
O terceiro gráfico foi criado com condições inciais aleatórias. | |||
== Resultados == | |||
Com o intuito de testar como o fator de difusão D afeta a evolução da equação de Cahn-Hilliard, comparamos os resultados para os coeficientes de difusão 1, 0.1, 0.01 e 0.001 e analisamos seus gráficos. | |||
[[Arquivo:coeficientes.png|500px|thumb|center| Gráfico 1: Resultados da simulação variando os coeficientes de difusão (D) para tempos máximos diferentes, <math>\gamma=3.4/128,\Delta t = 1/500000</math>]] | |||
Os gráficos representam a concentração dos fluídos (eixo y), pela posição em que elas se encontram no espaço (eixo x) e a evolução temporal do comportamento da mistura está representada pelas linhas coloridas, com o menor tempo representado pela linha azul (0.00001) que evolui até a linha roxa (0.1); | |||
Nos gráficos, é possível observar que quanto maior o coeficiente de difusão maior é a velocidade em que a mistura atinge a estabilidade. Além disso, vemos que valores baixos de t produzem soluções mais íngremes que valores altos de t. | |||
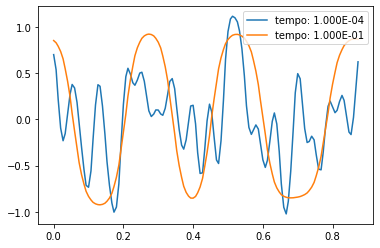
[[Arquivo:ContornoperiodicoeqCahnHilard.png|500px|thumb|center|Gráfico 2: Resultados da simulação utilizando contornos periódicos com valores iniciais iguais ao gráfico 1 com coeficiente de difusão igual a 1]] | |||
O segundo gráfico é interessante para observarmos como ela se comporta quando não há adição de matéria ao problema. | |||
[[Arquivo:NumerosaleatoriosCahnHIllard.png|500px|thumb|center|Gráfico 3: Resultados da simulação utilizando contornos periódicos com números aleatórios como valores iniciais]] | |||
Os números aleatórios oferecem uma boa condição inicial para entender como a equação funciona, percebemos que a estabilidade se aproxima a uma senoide. | |||
== Discussão de Resultados == | |||
Era de se esperar que ao longo das iterações a inclinação das concentrações fossem menos acentuadas, como ocorre em equações de difusão normais. Porém, o que diferencia é que para tempos grandes, após atingida a estabilidade, uma difusão normal apresenta apenas uma fase enquanto a espinodal permanece contendo duas. Podemos observar nas situações dos gráficos 1 e 2 que conforme evoluímos temporalmente, a derivada primeira da curva vai diminuindo próxima ao centro do gráfico até chegar a estabilidade. | |||
Uma propriedade observada no gráfico 1 e 2 é a de que os valores das soluções obtidas utilizando o método FTCS excedem os valores máximos e mínimos permitidos ( C=1 e C=-1), se estivesse modelando uma situação real isso iria contra a lei de conservação de massa, o que pode ocasionar erros nos resultados que exigem uma grande precisão. | |||
O método FTCS explícito limita-se por causa da condição de estabilidade, por isso esse método não é recomendado para modelos com alto <math>\gamma</math>. Para tais modelos, o método FTCS implícito é mais recomendado por ser incondicionalmente estável. | |||
== Implementção == | |||
<source lang="python"> | |||
import matplotlib.pyplot as plt | |||
def vector_declaration(L,dx): | |||
c = [[],[]] # vetor concentração | |||
espaco = [] | |||
# Condições iniciais | |||
for i in range(int(L/dx)+4):##+4 pois usaremos dois valores antes e depois do ultimo elemento do vetor c | |||
if (i<1/2*L/dx+2): | |||
c[0].append(-1) | |||
c[1].append(-1) | |||
else: | |||
c[0].append(1) | |||
c[1].append(1) | |||
espaco.append(round(i/150,3)) | |||
return c, espaco | |||
def random_vector_declaration(L,dx): | |||
c, espaco = vector_declaration(L, dx) | |||
a = c[0][:] | |||
random.shuffle(a) | |||
return [a[:],a[:]], espaco | |||
def CH_periodic_equation(gamma,D,dx,dt,L,TEMPO_MAX,f=vector_declaration, | |||
plot_intervals:list = []): | |||
c, espaco = f(L, dx) | |||
i = 0 | |||
j = 0 | |||
for time in [t*dt/TEMPO_MAX for t in range(int(TEMPO_MAX/dt))]: | |||
for l in range(len(c[1])): | |||
if l == len(c[1])-2: | |||
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3 | |||
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1] | |||
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][0] | |||
elif l == len(c[1])-1: | |||
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][0]**3 | |||
c2 = -c[i][l-1] + 2*c[i][l] - c[i][0] | |||
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][0] + c[i][1] | |||
else: | |||
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3 | |||
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1] | |||
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][l+2] | |||
c[1-i][l] = D*dt/(dx**2)*(c1+c2-gamma**2*c3/(dx**2)) + c[i][l] | |||
i = 1-i | |||
try: | |||
if plot_intervals[j]+dt>= time >= plot_intervals[j]-dt: | |||
plt.plot(espaco,c[1-i], label = "tempo: " + "{0:1.3E}".format(time)) | |||
j+=1 | |||
except IndexError: | |||
plt.legend() | |||
plt.show() | |||
break | |||
def CH_equation(gamma, D, dx, dt, L, TEMPO_MAX): # resolução numérica da equação | |||
c, espaco = vector_declaration(L, dx) | |||
i = 0 | |||
for time in [t*dt/TEMPO_MAX for t in range(int(TEMPO_MAX/dt))]: | |||
for l in range(2,len(c[1][2:-2])): | |||
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3 | |||
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1] | |||
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][l+2] | |||
c[1-i][l] = D*dt/(dx**2)*(c1+c2-gamma**2*c3/(dx**2)) + c[i][l] | |||
i = 1-i | |||
return(espaco[2:-2],c[1-i][2:-2]) ##retirando os elementos a mais do vetor | |||
tempo=1 | |||
tamanho=1 | |||
Difuse= 1 | |||
gamma=3.4*1/128 | |||
dt=1/2200000 | |||
dx = 1/128 | |||
</source> | |||
Gráfico 1 | |||
<source> | |||
figure, axis = plt.subplots(2, 2) | |||
plt.figure(dpi=500) | |||
: | axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000)) | ||
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000)) | |||
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000)) | |||
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100)) | |||
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10)) | |||
axis[0, 0].legend(loc="upper left", prop={'size': 6}) | |||
: | axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000)) | ||
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000)) | |||
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000)) | |||
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100)) | |||
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10)) | |||
axis[0, 1].legend(loc="upper left", prop={'size': 6}) | |||
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000)) | |||
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000)) | |||
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000)) | |||
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100)) | |||
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10)) | |||
axis[1, 0].legend(loc="upper left", prop={'size': 6}) | |||
: | axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000)) | ||
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000)) | |||
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000)) | |||
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100)) | |||
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10)) | |||
axis[1, 1].legend(loc="upper left", prop={'size': 6}) | |||
plt.show() | |||
= | plt.savefig('graficosDIFUSAO.png', dpi=500) | ||
</source> | |||
Gráfico 2 | |||
<source> | |||
: | plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000)) | ||
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000)) | |||
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100)) | |||
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10)) | |||
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/1), label = "tempo: " + str(tempo/1)) | |||
plt.show() | |||
</source> | |||
Gráfico 3 | |||
<source> | |||
CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10 + dt, random_vector_declaration, [tempo/10000, tempo/10]) | |||
</source> | |||
== Referências == | == Referências == | ||
[1] SIBBING, Zimo. '''Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions''', tese de bacharelado, 2015. https://repository.tudelft.nl/islandora/object/uuid%3A04732ecc-5e5b-4334-8f46-5cc4df93c0df | |||
[2] Spinodal Decomposition, disponível em: https://en.wikipedia.org/wiki/Spinodal_decomposition | |||
[3] MARKUS, Wilczek. '''The Cahn-Hilliard Equation''', 2015. | |||
[4] CAHN, John W.; HILLIARD, John E. '''Free Energy of a Nonuniform System. I. Interfacial Free Energy'''. The Journal of Chemical Physics, 1958. | |||
[5] CAHN, John W.; HILLIARD, John E. '''Spinodal decomposition: A reprise'''Acta Metallurgica, Volume 19, Issue 2, 1971 | |||
[6] Lei de Fick, disponível em: https://pt.wikipedia.org/wiki/Lei_de_Fick | |||
[7] Cahn-Hilliard Equation, disponível em: https://pt.qaz.wiki/wiki/Cahn%E2%80%93Hilliard_equation | |||
[8] Daniel V. Schroeder. An Introduction to Thermal Physics. Addison-Wesley, 1999. | |||
[9] Dongsun Lee, Joo-Youl Huh, Darae Jeong, Jaemin Shin, Ana Yun, and Junseok Kim. Physical, mathematical, and numerical derivations of the Cahn-Hilliard equation. Computational Materials Science, 2014. | |||
[10] Neumann Boundary Condition, disponível em: https://en.wikipedia.org/wiki/Neumann_boundary_condition | |||
Edição atual tal como às 19h59min de 26 de abril de 2021
Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss
O objetivo deste trabalho é resolver computacionalmente a equação de Cahn-Hilliard, que descreve o processo de decomposição espinodal de uma mistura binária, e analisar como é seu comportamento com diferentes coeficientes de difusão, utilizando o método FTCS (Forward Time Centered Space). O trabalho foi inspirado no artigo de Sibbing[1].
Decomposição Espinodal
Decomposição espinodal é o nome dado ao processo no qual uma pequena perturbação de um sistema faz com que uma fase homogênea termodinamicamente instável diminua sua energia e separe-se espontaneamente em duas outras fases coexistentes, esse é um processo que ocorre sem nucleação, ou seja, é instantâneo. Ela é observada, por exemplo, em misturas de metais ou polímeros [2].
A Equação de Cahn-Hilliard
A equação de Cahn-Hilliard é uma equação que descreve o processo de separação de fase entre dois componentes de um fluido binário que se separam de maneira espontânea. Com o intuito de deduzirmos essa equação, consideraremos - de início - uma mistura binária de dois componentes A e B descritas pelas concentrações dos fluidos e , respectivamente. [1]
Além disso, podemos considerar que - para uma mistura binária - e portanto podemos simplificar para apenas uma concentração :
Tendo isso em vista, podemos agora utilizar a primeira lei de Fick da difusão:
juntamente da equação da continuidade:
Onde é o coeficiente de difusão e é o fluxo de difusão de concentração da mistura. Em seguida, ao combinarmos ambas as equações anteriores o resultado gera a segunda lei de Fick da difusão:
A partir dessa equação - como não há a existência de um gradiente de concentração espacial - pode-se esperar que não ocorra mudança na concentração da mistura. No entanto, observa-se que quando a separação de fases ocorre, a difusão demonstra ser contrária ao gradiente de concentração, o que não condiz com a equação anterior. Tendo isso em vista, conclui-se que a concentração não pode ser a razão da difusão, portanto outra força deve estar presente. E, nesse caso, encontrou-se que a principal força responsável pela difusão negativa (difusão que "o estado de equilíbrio é um sistema de duas fases separadas por uma interface", seção 1.1 de [1]) é o potencial químico (de acordo com Cahn e Hilliard, 1958). Portanto, outra equação pode ser derivada para generalizar a primeira lei de Fick:
Onde é a mobilidade das partículas (análoga à D) e é o potencial químico. Com essa nova equação podemos agora também deduzir uma nova equação para a segunda lei de Fick [3]:
Nessa equação, podemos usar a definição do potencial químico através da densidade da energia livre de Gibbs como:
Onde é a densidade da energia livre de Gibbs e é a concentração (de acordo com Schroeder, 1999).
Tendo em vista a substituição do termo por um termo que envolva a concentração dos fluidos, utiliza-se uma equação que descreve a densidade de energia desse sistema através da concentração dos mesmos (derivado em [3]):
Nesse caso, é a energia livre de Gibbs, é a densidade de energia livre devido à contribuições de ambas as fases homogêneas e é a densidade de energia livre devido ao gradiente de concentração.
Além disso, a função - de acordo com [8] - possui o potencial de um poço de potencial duplo. Neste poço, representa a concentração em escala e está relacionada à temperatura da mistura, que decide se a separação de fases irá - ou não - ocorrer. Esta função pode ser representada pela seguinte equação:
Levando essas informações em conta e - utilizando um parâmetro análogo à largura da interface - que é descrito por é possível encontrar uma equação que descreve a densidade de energia livre de Gibbs para um sistema com duas fases.
Com essas igualdades agora se torna possível o cálculo de em função da concentração dos fluidos:
Finalmente - utilizando a última expressão encontrada - torna-se possível reescrever o potencial químico em função da mobilidade de suas partículas () e a concentração do fluido:
Essa equação final é chamada de equação de Cahn-Hilliard. A equação dependente da difusão é análoga e também funcional e pode ser escrita em relação ao potencial químico:
Método FTCS (Forward Time Centered Space)
O FTCS é um método numérico utilizado para resolver equações diferenciais parciais, tais como a difusão do calor e do transporte de massa, traduzindo, significa "Progressivo no tempo, centrado no espaço". Uma das formas que o método pode ser utilizado é a forma explícita que está descrita abaixo.
FTCS Explicito
Para difusão:
Implementação da equação de Cahn-Hilliard 1D pelo método FTCS explícito
substituindo por (potencial químico)
Condição de Estabilidade
A estabilidade dessa equação mostra-se muito mais complicada de se estipular por ela ser uma equação diferencial de quarta ordem se comparada a equação de difusão, Portanto só iremos analisar a seção 3.3 (Experimental and theoretical stability conditions) do artigo Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions [1].
Após a linearização e aplicação do teorema de Gershgorin temos que a condição para estabilidade da equação linear para é:
Importante atentar que essa é a condição de estabilidade somente para a equação de Cahn-Hilliard linearizada, não para a original. Tanto que a literatura sobre a equação propõem que , que é o que acontece na condição estabilidade linear quando .
O artigo compara os dados experimentais de estabilidade com a estabilidade da equação linearizada relacionado na seção 3.3.4 e conclui que para valores de a condição teórica encontrada a partir da linearização é uma boa aproximação.
Condição de Contorno
Foram utilizadas duas condições de contorno para produzir os resultados, o gráfico 1 foi criado estabelecendo que:
Onde L é o comprimento da grid, essa condição de Dirichlet adiciona matéria ao problema, mas é uma forma prática de analisar diferentes coeficientes de difusão. Para os demais resultados foram utilizadas condições de contorno periódicas.
Condições Iniciais
Para os resultados do gráfico 1 e 2 foram utilizadas como condições iniciais a concentração -1 para a primeira metade de L e 1 para a segunda metade:
O terceiro gráfico foi criado com condições inciais aleatórias.
Resultados
Com o intuito de testar como o fator de difusão D afeta a evolução da equação de Cahn-Hilliard, comparamos os resultados para os coeficientes de difusão 1, 0.1, 0.01 e 0.001 e analisamos seus gráficos.
Os gráficos representam a concentração dos fluídos (eixo y), pela posição em que elas se encontram no espaço (eixo x) e a evolução temporal do comportamento da mistura está representada pelas linhas coloridas, com o menor tempo representado pela linha azul (0.00001) que evolui até a linha roxa (0.1);
Nos gráficos, é possível observar que quanto maior o coeficiente de difusão maior é a velocidade em que a mistura atinge a estabilidade. Além disso, vemos que valores baixos de t produzem soluções mais íngremes que valores altos de t.
O segundo gráfico é interessante para observarmos como ela se comporta quando não há adição de matéria ao problema.
Os números aleatórios oferecem uma boa condição inicial para entender como a equação funciona, percebemos que a estabilidade se aproxima a uma senoide.
Discussão de Resultados
Era de se esperar que ao longo das iterações a inclinação das concentrações fossem menos acentuadas, como ocorre em equações de difusão normais. Porém, o que diferencia é que para tempos grandes, após atingida a estabilidade, uma difusão normal apresenta apenas uma fase enquanto a espinodal permanece contendo duas. Podemos observar nas situações dos gráficos 1 e 2 que conforme evoluímos temporalmente, a derivada primeira da curva vai diminuindo próxima ao centro do gráfico até chegar a estabilidade.
Uma propriedade observada no gráfico 1 e 2 é a de que os valores das soluções obtidas utilizando o método FTCS excedem os valores máximos e mínimos permitidos ( C=1 e C=-1), se estivesse modelando uma situação real isso iria contra a lei de conservação de massa, o que pode ocasionar erros nos resultados que exigem uma grande precisão.
O método FTCS explícito limita-se por causa da condição de estabilidade, por isso esse método não é recomendado para modelos com alto . Para tais modelos, o método FTCS implícito é mais recomendado por ser incondicionalmente estável.
Implementção
import matplotlib.pyplot as plt
def vector_declaration(L,dx):
c = [[],[]] # vetor concentração
espaco = []
# Condições iniciais
for i in range(int(L/dx)+4):##+4 pois usaremos dois valores antes e depois do ultimo elemento do vetor c
if (i<1/2*L/dx+2):
c[0].append(-1)
c[1].append(-1)
else:
c[0].append(1)
c[1].append(1)
espaco.append(round(i/150,3))
return c, espaco
def random_vector_declaration(L,dx):
c, espaco = vector_declaration(L, dx)
a = c[0][:]
random.shuffle(a)
return [a[:],a[:]], espaco
def CH_periodic_equation(gamma,D,dx,dt,L,TEMPO_MAX,f=vector_declaration,
plot_intervals:list = []):
c, espaco = f(L, dx)
i = 0
j = 0
for time in [t*dt/TEMPO_MAX for t in range(int(TEMPO_MAX/dt))]:
for l in range(len(c[1])):
if l == len(c[1])-2:
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1]
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][0]
elif l == len(c[1])-1:
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][0]**3
c2 = -c[i][l-1] + 2*c[i][l] - c[i][0]
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][0] + c[i][1]
else:
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1]
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][l+2]
c[1-i][l] = D*dt/(dx**2)*(c1+c2-gamma**2*c3/(dx**2)) + c[i][l]
i = 1-i
try:
if plot_intervals[j]+dt>= time >= plot_intervals[j]-dt:
plt.plot(espaco,c[1-i], label = "tempo: " + "{0:1.3E}".format(time))
j+=1
except IndexError:
plt.legend()
plt.show()
break
def CH_equation(gamma, D, dx, dt, L, TEMPO_MAX): # resolução numérica da equação
c, espaco = vector_declaration(L, dx)
i = 0
for time in [t*dt/TEMPO_MAX for t in range(int(TEMPO_MAX/dt))]:
for l in range(2,len(c[1][2:-2])):
c1 = c[i][l-1]**3 - 2*c[i][l]**3 + c[i][l+1]**3
c2 = -c[i][l-1] + 2*c[i][l] - c[i][l+1]
c3 = c[i][l-2] -4*c[i][l-1] + 6*c[i][l] - 4*c[i][l+1] + c[i][l+2]
c[1-i][l] = D*dt/(dx**2)*(c1+c2-gamma**2*c3/(dx**2)) + c[i][l]
i = 1-i
return(espaco[2:-2],c[1-i][2:-2]) ##retirando os elementos a mais do vetor
tempo=1
tamanho=1
Difuse= 1
gamma=3.4*1/128
dt=1/2200000
dx = 1/128
Gráfico 1
figure, axis = plt.subplots(2, 2)
plt.figure(dpi=500)
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[0, 0].plot(*CH_equation(gamma, Difuse, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[0, 0].legend(loc="upper left", prop={'size': 6})
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[0, 1].plot(*CH_equation(gamma, Difuse/10, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[0, 1].legend(loc="upper left", prop={'size': 6})
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[1, 0].plot(*CH_equation(gamma, Difuse/100, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[1, 0].legend(loc="upper left", prop={'size': 6})
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100000), label = "tempo: " + str(tempo/100000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
axis[1, 1].plot(*CH_equation(gamma, Difuse/1000, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
axis[1, 1].legend(loc="upper left", prop={'size': 6})
plt.show()
plt.savefig('graficosDIFUSAO.png', dpi=500)Gráfico 2
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10000), label = "tempo: " + str(tempo/10000))
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/1000), label = "tempo: " + str(tempo/1000))
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/100), label = "tempo: " + str(tempo/100))
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10), label = "tempo: " + str(tempo/10))
plt.plot(*CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/1), label = "tempo: " + str(tempo/1))
plt.show()Gráfico 3
CH_periodic_equation(gamma, Difuse, dx, dt, tamanho, tempo/10 + dt, random_vector_declaration, [tempo/10000, tempo/10])Referências
[1] SIBBING, Zimo. Numerical methods for the implentation of the Cahn-Hilliard equation in one dimension and a dynamic boundary condition in two dimensions, tese de bacharelado, 2015. https://repository.tudelft.nl/islandora/object/uuid%3A04732ecc-5e5b-4334-8f46-5cc4df93c0df
[2] Spinodal Decomposition, disponível em: https://en.wikipedia.org/wiki/Spinodal_decomposition
[3] MARKUS, Wilczek. The Cahn-Hilliard Equation, 2015.
[4] CAHN, John W.; HILLIARD, John E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. The Journal of Chemical Physics, 1958.
[5] CAHN, John W.; HILLIARD, John E. Spinodal decomposition: A repriseActa Metallurgica, Volume 19, Issue 2, 1971
[6] Lei de Fick, disponível em: https://pt.wikipedia.org/wiki/Lei_de_Fick
[7] Cahn-Hilliard Equation, disponível em: https://pt.qaz.wiki/wiki/Cahn%E2%80%93Hilliard_equation
[8] Daniel V. Schroeder. An Introduction to Thermal Physics. Addison-Wesley, 1999.
[9] Dongsun Lee, Joo-Youl Huh, Darae Jeong, Jaemin Shin, Ana Yun, and Junseok Kim. Physical, mathematical, and numerical derivations of the Cahn-Hilliard equation. Computational Materials Science, 2014.
[10] Neumann Boundary Condition, disponível em: https://en.wikipedia.org/wiki/Neumann_boundary_condition














































![{\displaystyle {\frac {\gamma }{\Delta x}}\in [0.25,8]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4796f54e87945ae8d27d4ddb132ec208953958bc)