Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou: mudanças entre as edições
(→N=3) |
|||
| (73 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo:''' Paula Pandolfo, Ramiro de Souza, Samuel Dieterich e Wallace Carvalho | '''Grupo:''' Paula Pandolfo, Ramiro de Souza, Samuel Dieterich e Wallace Carvalho | ||
'''Objetivo:''' Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas as análises de resultados serão restritas aos casos unidimensionais, por simplicidade. | '''Objetivo:''' Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas as análises de resultados serão restritas aos casos unidimensionais, por simplicidade. | ||
== Introdução == | == Introdução == | ||
| Linha 10: | Linha 10: | ||
O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo <ref name=FPUToriginal>Fermi, E.; Pasta, J.; Ulam, S. (1955). "Studies of Nonlinear Problems" (PDF). Document LA-1940. Los Alamos National Laboratory. [Acessado 02 Maio 2022]. [http://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf]</ref>, que relataram o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).<ref name=WeThankMTsingou>Grant, V. "We Thank Miss Mary Tsingou", National Security Science. Winter 2020: pp. 36-43. [Acessado 02 Maio 2022]. [https://www.lanl.gov/discover/publications/national-security-science/2020-winter/mary-tsingou.shtml]</ref> | O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo <ref name=FPUToriginal>Fermi, E.; Pasta, J.; Ulam, S. (1955). "Studies of Nonlinear Problems" (PDF). Document LA-1940. Los Alamos National Laboratory. [Acessado 02 Maio 2022]. [http://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf]</ref>, que relataram o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).<ref name=WeThankMTsingou>Grant, V. "We Thank Miss Mary Tsingou", National Security Science. Winter 2020: pp. 36-43. [Acessado 02 Maio 2022]. [https://www.lanl.gov/discover/publications/national-security-science/2020-winter/mary-tsingou.shtml]</ref> | ||
A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores lineares acoplados. Em seguida, compararemos esses resultados com simulações computacionais, a fim de exemplificar visualmente seu significado. Após apresentar as fundações teóricas desses casos mais simples em que as forças são lineares, trataremos do problema de FPUT em si, examinando a situação em que a interação não-linear se dá através de um termo quadrático nas coordenadas generalizadas utilizadas. Tal tratamento tem de ser majoritariamente computacional, já que as equações diferenciais envolvidas não são, em geral, fáceis de se resolver. | A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores lineares acoplados. Em seguida, compararemos esses resultados com simulações computacionais, a fim de exemplificar visualmente seu significado. Após apresentar as fundações teóricas desses casos mais simples em que as forças são lineares, trataremos do problema de FPUT em si, examinando a situação em que a interação não-linear se dá através de um termo quadrático nas coordenadas generalizadas utilizadas. Tal tratamento tem de ser majoritariamente computacional, já que as equações diferenciais envolvidas não são, em geral, fáceis de se resolver analiticamente. | ||
== Osciladores Lineares Acoplados== | == Osciladores Lineares Acoplados== | ||
Um modelo geral de sistema unidimensional de osciladores lineares acoplados é ilustrado pela '''Figura 1'''. | Um modelo geral de sistema unidimensional de osciladores lineares acoplados é ilustrado pela '''Figura 1'''. | ||
<center> | <center> | ||
| Linha 20: | Linha 20: | ||
</center> | </center> | ||
Cada partícula possui duas vizinhas com as quais interage por meio das molas, exceto as partículas localizadas nos extremos da cadeia, que possuem apenas uma partícula vizinha cada. As interações das partículas dos extremos das cadeias se restringem, portanto, à interação com uma vizinha e com uma mola conectada a uma das paredes externas à cadeia. Como este problema é unidimensional, a posição de cada partícula pode ser descrita por apenas um grau de liberdade. Vamos escolher os deslocamentos <math>x_i</math> em relação à respectiva posição de equilíbrio da partícula <math>i</math> como nossas coordenadas generalizadas, definindo como positivos os deslocamentos para a direita e negativos para a esquerda. No total, um sistema com <math>N</math> partículas terá, portanto, <math>N</math> graus de liberdade. Vamos tratar aqui o caso em que as forças das molas são lineares, i.e., dadas | Cada partícula possui duas vizinhas com as quais interage por meio das molas, exceto as partículas localizadas nos extremos da cadeia, que possuem apenas uma partícula vizinha cada. As interações das partículas dos extremos das cadeias se restringem, portanto, à interação com uma vizinha e com uma mola conectada a uma das paredes externas à cadeia. Como este problema é unidimensional, a posição de cada partícula pode ser descrita por apenas um grau de liberdade. Vamos escolher os deslocamentos <math>x_i</math> em relação à respectiva posição de equilíbrio da partícula <math>i</math> como nossas coordenadas generalizadas, definindo como positivos os deslocamentos para a direita e negativos para a esquerda. No total, um sistema com <math>N</math> partículas terá, portanto, <math>N</math> graus de liberdade. Vamos tratar aqui o caso em que as forças das molas são lineares, seguindo a lei de Hooke; i.e., forças dadas pela forma <math>F=-kx</math>. '''Além disso, para simplificar e minimizar o número de parâmetros das simulações, vamos considerar que, em todos os casos mostrados, todas as molas possuem as mesmas constantes de acoplamento linear <math>k</math> e todas as partículas possuem as mesmas massas <math>m</math>'''. | ||
=== N=2 === | === N=2 === | ||
| Linha 31: | Linha 31: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
m\ddot{x}_{1} &= -kx_{1} - k(x_{1}-x_{2}) \\ | m\ddot{x}_{1} &= -kx_{1} - k(x_{1}-x_{2}) \\ | ||
m\ddot{x}_{2} &= -kx_{2} - k(x_{2}-x_{1}) \quad (1)\\ | m\ddot{x}_{2} &= -kx_{2} - k(x_{2}-x_{1})\text{.} \quad (1)\\ | ||
\end{align}</math> | \end{align}</math> | ||
| Linha 40: | Linha 40: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{1}(t) &= A_{1}e^{-i\omega t} \\ | x_{1}(t) &= A_{1}e^{-i\omega t} \\ | ||
x_{2}(t) &= A_{2}e^{-i\omega t} \quad (2) | x_{2}(t) &= A_{2}e^{-i\omega t}\text{,} \quad (2) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
onde <math>A_{1}</math> e <math>A_{2}</math> são constantes e <math>\omega</math> é uma frequência angular ainda indeterminada. Essa suposição é fisicamente justificável: sabemos que as soluções são oscilatórias, e exponenciais imaginárias podem ser escritas em termos de senos e cossenos pela fórmula de Euler. Se substituirmos as expressões em (2) na equação (1) e rearranjarmos os termos, obteremos: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
-mw^{2}A_{1}e^{-i\omega t} + 2kA_{1}e^{-i\omega t} -kA_{2}e^{-i\omega t} &= 0 \\ | -mw^{2}A_{1}e^{-i\omega t} + 2kA_{1}e^{-i\omega t} -kA_{2}e^{-i\omega t} &= 0 \\ | ||
-mw^{2}A_{2}e^{-i\omega t} + 2kA_{2}e^{-i\omega t} -kA_{1}e^{-i\omega t} &= 0 \\ | -mw^{2}A_{2}e^{-i\omega t} + 2kA_{2}e^{-i\omega t} -kA_{1}e^{-i\omega t} &= 0\text{.} \\ | ||
\end{align}</math> | \end{align}</math> | ||
| Linha 55: | Linha 55: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
(2k-mw^{2})&A_{1} &-kA_{2} &= 0 \\ | (2k-mw^{2})&A_{1} &-kA_{2} &= 0 \\ | ||
-k&A_{1} &+(2k-mw^{2})A_{2} &= 0 \quad (3)\\ | -k&A_{1} &+(2k-mw^{2})A_{2} &= 0\text{.} \quad (3)\\ | ||
\end{align}</math> | \end{align}</math> | ||
| Linha 63: | Linha 63: | ||
(2k-mw^{2}) & -k \\ | (2k-mw^{2}) & -k \\ | ||
-k & (2k-mw^{2}) | -k & (2k-mw^{2}) | ||
\end{vmatrix} = 0 </math> | \end{vmatrix} = 0\text{.} </math> | ||
O resultado desse determinante ser igual a zero é uma equação quadrática simples em <math>\omega^2</math>, sendo as soluções facilmente obtidas. Como para cada solução <math>\omega</math> existe uma solução <math>-\omega</math>, apresentaremos apenas o módulo das frequências: | O resultado desse determinante ser igual a zero é uma equação quadrática simples em <math>\omega^2</math>, sendo as soluções facilmente obtidas. Como para cada solução <math>\omega</math> existe uma solução <math>-\omega</math>, apresentaremos apenas o módulo das frequências: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\omega_{1} = \sqrt{\frac{k}{m}} \quad \quad \omega_{2} = \sqrt{\frac{3k}{m}} \quad (4) | \omega_{1} = \sqrt{\frac{k}{m}} \quad \text{,} \quad \omega_{2} = \sqrt{\frac{3k}{m}}\text{.} \quad (4) | ||
\end{align} </math> | \end{align} </math> | ||
<math>\omega_{1}</math> e <math>\omega_{2}</math> são as frequências características ou autofrequências do sistema. As soluções mais gerais do sistema de equações diferenciais lineares (1) vão ser então combinações lineares das soluções (2) com as frequências dadas por (4): | <math>\omega_{1}</math> e <math>\omega_{2}</math> são então denominadas as frequências características ou autofrequências do sistema. As soluções mais gerais do sistema de equações diferenciais lineares (1) vão ser então combinações lineares das soluções (2) com as frequências dadas por (4): | ||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{1}(t) = a_{1}^{1}e^{i\omega_{1} t} &+ a_{1}^{2}e^{-i\omega_{1} t} &+ a_{1}^{3}e^{i\omega_{2} t} &+ a_{1}^{4}e^{-i\omega_{2} t} \\ | x_{1}(t) = a_{1}^{1}e^{i\omega_{1} t} &+ a_{1}^{2}e^{-i\omega_{1} t} &+ a_{1}^{3}e^{i\omega_{2} t} &+ a_{1}^{4}e^{-i\omega_{2} t} \\ | ||
x_{2}(t) = a_{2}^{1}e^{i\omega_{1} t} &+ a_{2}^{2}e^{-i\omega_{1} t} &+ a_{2}^{3}e^{i\omega_{2} t} &+ a_{2}^{4}e^{-i\omega_{2} t} \quad (5) | x_{2}(t) = a_{2}^{1}e^{i\omega_{1} t} &+ a_{2}^{2}e^{-i\omega_{1} t} &+ a_{2}^{3}e^{i\omega_{2} t} &+ a_{2}^{4}e^{-i\omega_{2} t}\text{.} \quad (5) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 81: | Linha 81: | ||
Nota-se que cada uma das soluções é uma superposição (em geral) complicada que envolve as duas autofrequências. Isso é uma consequência direta do acoplamento presente no sistema (1). Para eliminar este acoplamento, vamos definir novas variáveis: <math>\eta_{1} = x_{1} + x_{2}</math> e <math>\eta_{2} = x_{1} - x_{2}</math>, ou | Nota-se que cada uma das soluções é uma superposição (em geral) complicada que envolve as duas autofrequências. Isso é uma consequência direta do acoplamento presente no sistema (1). Para eliminar este acoplamento, vamos definir novas variáveis: <math>\eta_{1} = x_{1} + x_{2}</math> e <math>\eta_{2} = x_{1} - x_{2}</math>, ou | ||
:<math> | :<math> x_{1} = \frac{\eta_{1} + \eta_{2}}{2} \quad \text{,} \quad x_{2} = \frac{\eta_{1} - \eta_{2}}{2}\text{.}</math> | ||
x_{1} = \frac{\eta_{1} + \eta_{2}}{2} \\ | |||
x_{2} = \frac{\eta_{1} - \eta_{2}}{2} | |||
\ | |||
</math> | |||
Substituindo essas expressões no sistema de equações (1): | Substituindo essas expressões no sistema de equações (1), ficamos com: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
m(\ddot{\eta}_{1} + \ddot{\eta}_{2}) + k\eta_{1} + 3k\eta_{2} = 0 \\ | &m(\ddot{\eta}_{1} + \ddot{\eta}_{2}) + k\eta_{1} + 3k\eta_{2} = 0 \\ | ||
m(\ddot{\eta}_{1} - \ddot{\eta}_{2}) + k\eta_{1} - 3k\eta_{2} = 0 | &m(\ddot{\eta}_{1} - \ddot{\eta}_{2}) + k\eta_{1} - 3k\eta_{2} = 0\text{.} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Se somarmos as duas equações acima e subtrairmos a segunda da primeira, obtemos, respectivamente: | Se somarmos as duas equações acima, e se subtrairmos a segunda da primeira, obtemos, respectivamente: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
m\ddot{\eta}_{1} + k\eta_{1} = 0 \\ | &m\ddot{\eta}_{1} + k\eta_{1} = 0 \\ | ||
m\ddot{\eta}_{2} + 3k\eta_{2} = 0 | &m\ddot{\eta}_{2} + 3k\eta_{2} = 0\text{.} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 107: | Linha 103: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\eta_{1}(t) &= c_{1}e^{i\omega_{1}t} + c_{2}e^{-i\omega_{1}t} \\ | \eta_{1}(t) &= c_{1}e^{i\omega_{1}t} + c_{2}e^{-i\omega_{1}t} \\ | ||
\eta_{2}(t) &= c_{3}e^{i\omega_{2}t} + c_{4}e^{-i\omega_{2}t} \quad (6) | \eta_{2}(t) &= c_{3}e^{i\omega_{2}t} + c_{4}e^{-i\omega_{2}t}\text{.} \quad (6) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
<math>\eta_{1}</math> e <math>\eta_{2}</math> são chamadas de coordenadas normais. Por definição, são coordenadas que desacoplam as equações diferenciais do sistema e possuem soluções com frequências únicas, bem definidas. Sempre podem ser escritas como algum tipo de combinação linear das coordenadas originais. De modo semelhante, as coordenadas usuais do sistema sempre podem ser escritas como combinações lineares das coordenadas normais. No caso geral, para mais partículas, | <math>\eta_{1}</math> e <math>\eta_{2}</math> são chamadas de coordenadas normais. Por definição, são coordenadas que desacoplam as equações diferenciais do sistema e possuem soluções com frequências únicas, bem definidas. Sempre podem ser escritas como algum tipo de combinação linear das coordenadas originais. De modo semelhante, as coordenadas usuais do sistema sempre podem ser escritas como combinações lineares das coordenadas normais. No caso geral, para mais partículas, a combinação linear dos deslocamentos <math>x_i</math> que produz as coordenadas normais é trabalhosa de se encontrar. Note-se que, no caso de duas partículas, é simples encontrá-las meramente por inspeção. Se impusermos as condições iniciais <math>x_{1}(0) = x_{2}(0)</math> e <math>\dot{x}_{1}(0) = \dot{x}_{2}(0)</math>, <math>\eta_{2}(0) = x_{1}(0) - x_{2}(0) = 0</math> e as constantes <math>c_{3}</math> e <math>c_{4}</math> vão ser iguais a zero, o que implica <math>\eta_{2}(t) = 0</math>, para todo <math>t</math>. Esse primeiro modo normal corresponderá a uma oscilação simétrica, em que as duas partículas oscilarão em fase, com frequência <math>\omega_{1}</math>. De modo semelhante, se impusermos as condições iniciais <math>x_{1}(0) = -x_{2}(0)</math> e <math>\dot{x}_{1}(0) = -\dot{x}_{2}(0)</math>, <math>\eta_{1}(t) = 0</math>, para todo <math>t</math>, e as partículas oscilarão fora de fase, com frequência <math>\omega_{2}</math>. Pelas expressões dadas em (4) e pelas simulações abaixo, destaca-se que a frequência associada ao modo simétrico é menor do que a frequência do modo antissimétrico. Esse é um resultado geral de oscilações acopladas: quanto maior o grau de simetria da oscilação, menor o valor da frequência.<ref name=Marion2004/> | ||
Alguns resultados das simulações para os modos desse caso podem ser observados na '''Figura 2''' e na '''Figura 3'''. | Alguns resultados das simulações para os modos desse caso podem ser observados na '''Figura 2''' e na '''Figura 3'''. Fica evidente a menor frequência do modo simétrico em relação ao modo antissimétrico. Além disso, podemos observar a concordância com os valores teóricos encontrados para as frequências: <math>\omega_{1}=1</math> e <math>\omega_{2}= \sqrt{3}</math>. O modo simétrico consiste em uma oscilação em que as partículas estão em fase; no modo antissimétrico, as partículas oscilam fora de fase. | ||
<gallery class="center" mode=packed heights=250px> | <gallery class="center" mode=packed heights=250px> | ||
| Linha 139: | Linha 135: | ||
m\ddot{x}_{1} &= -kx_{1} - k(x_{1}-x_{2}) \\ | m\ddot{x}_{1} &= -kx_{1} - k(x_{1}-x_{2}) \\ | ||
m\ddot{x}_{2} &= -k(x_{2}-x_{1}) - k(x_{2}-x_{3}) \\ | m\ddot{x}_{2} &= -k(x_{2}-x_{1}) - k(x_{2}-x_{3}) \\ | ||
m\ddot{x}_{3} &= -kx_{3} - k(x_{3}-x_{2}) \quad (7)\\ | m\ddot{x}_{3} &= -kx_{3} - k(x_{3}-x_{2})\text{.} \quad\quad (7)\\ | ||
\end{align}</math> | \end{align}</math> | ||
Novamente, supomos soluções do tipo | |||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{1}(t) &= A_{1}e^{-i\omega t} \\ | x_{1}(t) &= A_{1}e^{-i\omega t} \\ | ||
x_{2}(t) &= A_{2}e^{-i\omega t} \\ | x_{2}(t) &= A_{2}e^{-i\omega t} \\ | ||
x_{3}(t) &= A_{3}e^{-i\omega t} \quad (8) | x_{3}(t) &= A_{3}e^{-i\omega t}\text{.} \quad (8) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Substituindo (8) em (7) e seguindo os mesmos passos feitos para <math>N=2</math> partículas: | Substituindo (8) em (7) e seguindo os mesmos passos feitos para <math>N=2</math> partículas, obteremos o sistema linear para os <math>A_i</math>: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
(2k-mw^{2})A_{1} &-kA_{2} &+0A_{3} &= 0 \\ | (2k-mw^{2})A_{1} &-kA_{2} &+0A_{3} &= 0 \\ | ||
-kA_{1} &+(2k-mw^{2})A_{2} &-kA_{3} &= 0 \\ | -kA_{1} &+(2k-mw^{2})A_{2} &-kA_{3} &= 0 \\ | ||
0A_{1} &-kA_{2} &+(2k-mw^{2})A_{3} &= 0 \\ | 0A_{1} &-kA_{2} &+(2k-mw^{2})A_{3} &= 0\text{.}\\ | ||
\end{align}</math> | \end{align}</math> | ||
O sistema de equações acima apenas terá soluções não triviais se o determinante dos coeficientes dos <math>A_{i}</math> for igual a zero | O sistema de equações acima apenas terá soluções não triviais se o determinante dos coeficientes dos <math>A_{i}</math> for igual a zero. Portanto: | ||
:<math>\begin{vmatrix} | :<math>\begin{vmatrix} | ||
| Linha 165: | Linha 161: | ||
-k & (2k-mw^{2}) &-k \\ | -k & (2k-mw^{2}) &-k \\ | ||
0 & -k & (2k-mw^{2}) | 0 & -k & (2k-mw^{2}) | ||
\end{vmatrix} = 0 </math> | \end{vmatrix} = 0 \text{.}</math> | ||
A equação resultante é <math>(2k-m\omega^{2})^3 - 2k^2(2k-m\omega^2) = 0</math>. Simples de ser resolvida analiticamente por fatoração, esta equação tem as soluções: | A equação resultante é <math>(2k-m\omega^{2})^3 - 2k^2(2k-m\omega^2) = 0</math>. Simples de ser resolvida analiticamente por fatoração, esta equação tem as soluções de módulo: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\omega_{1} = \sqrt{\frac{k}{m}(2-\sqrt{2})} \quad\quad \omega_{2} = \sqrt{\frac{2k}{m}} \quad\quad \omega_{3} = \sqrt{\frac{k}{m}(2+\sqrt{2})} \quad (9) | \omega_{1} = \sqrt{\frac{k}{m}(2-\sqrt{2})} \quad \text{,} \quad \omega_{2} = \sqrt{\frac{2k}{m}} \quad \text{,} \quad \omega_{3} = \sqrt{\frac{k}{m}(2+\sqrt{2})}\text{.} \quad (9) | ||
\end{align} </math> | \end{align} </math> | ||
Note-se que aqui já não é mais tão simples identificar as coordenadas normais. Além disso, embora tenha sido simples até aqui obter as autofrequências, o processo é tedioso e a equação característica | Note-se que aqui já não é mais tão simples identificar as coordenadas normais. Além disso, embora tenha sido simples até aqui obter as autofrequências, o processo é tedioso e a equação característica se torna cada vez mais difícl de se resolver analiticamente. | ||
Podemos escrever as soluções da seguinte forma, de modo semelhante a como fizemos para <math>N=2</math>: | Podemos escrever as soluções da seguinte forma, de modo semelhante a como fizemos para <math>N=2</math>: | ||
| Linha 180: | Linha 176: | ||
x_{1}(t) = a_{1}^{1}e^{i\omega_{1} t} &+ a_{1}^{2}e^{-i\omega_{1} t} &+ a_{1}^{3}e^{i\omega_{2} t} &+ a_{1}^{4}e^{-i\omega_{2} t} &+ a_{1}^{5}e^{i\omega_{3} t} &+ a_{1}^{6}e^{-i\omega_{3} t}\\ | x_{1}(t) = a_{1}^{1}e^{i\omega_{1} t} &+ a_{1}^{2}e^{-i\omega_{1} t} &+ a_{1}^{3}e^{i\omega_{2} t} &+ a_{1}^{4}e^{-i\omega_{2} t} &+ a_{1}^{5}e^{i\omega_{3} t} &+ a_{1}^{6}e^{-i\omega_{3} t}\\ | ||
x_{2}(t) = a_{2}^{1}e^{i\omega_{1} t} &+ a_{2}^{2}e^{-i\omega_{1} t} &+ a_{2}^{3}e^{i\omega_{2} t} &+ a_{2}^{4}e^{-i\omega_{2} t} &+ a_{2}^{5}e^{i\omega_{3} t} &+ a_{2}^{6}e^{-i\omega_{3} t} \\ | x_{2}(t) = a_{2}^{1}e^{i\omega_{1} t} &+ a_{2}^{2}e^{-i\omega_{1} t} &+ a_{2}^{3}e^{i\omega_{2} t} &+ a_{2}^{4}e^{-i\omega_{2} t} &+ a_{2}^{5}e^{i\omega_{3} t} &+ a_{2}^{6}e^{-i\omega_{3} t} \\ | ||
x_{3}(t) = a_{3}^{1}e^{i\omega_{1} t} &+ a_{3}^{2}e^{-i\omega_{1} t} &+ a_{3}^{3}e^{i\omega_{2} t} &+ a_{3}^{4}e^{-i\omega_{2} t} &+ a_{3}^{5}e^{i\omega_{3} t} &+ a_{3}^{6}e^{-i\omega_{3} t} \quad (10) | x_{3}(t) = a_{3}^{1}e^{i\omega_{1} t} &+ a_{3}^{2}e^{-i\omega_{1} t} &+ a_{3}^{3}e^{i\omega_{2} t} &+ a_{3}^{4}e^{-i\omega_{2} t} &+ a_{3}^{5}e^{i\omega_{3} t} &+ a_{3}^{6}e^{-i\omega_{3} t}\text{.} \quad (10) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Alguns resultados das simulações para os modos desse caso podem ser observados na '''Figura 6''', na '''Figura 7''' e na '''Figura 8'''. | Alguns resultados das simulações para os modos desse caso podem ser observados na '''Figura 6''', na '''Figura 7''' e na '''Figura 8'''. Nota-se, mais uma vez, que a menor frequência em relação aos demais modos é aquela associada ao modo simétrico. O modo simétrico consiste em uma oscilação em que todas as partículas estão em fase; no modo antissimétrico, as partículas 1 e 3 oscilam fora de fase, a 2 permanece parada. A novidade em relação ao caso de <math>N=2</math> é o surgimento de um novo modo, o modo 3, em que as partículas 1 e 3 oscilam em fase, e a partícula 2 oscila fora de fase em relação às partículas 1 e 3. | ||
<gallery class="center" mode=packed heights=250px> | <gallery class="center" mode=packed heights=250px> | ||
| Linha 213: | Linha 209: | ||
=== Caso geral === | === Caso geral === | ||
O formalismo lagrangeano fornece uma técnica poderosa para construir as equações de movimento para o caso geral de <math>N</math> partículas, bem como para facilitar o cálculo das coordenadas normais e das autofrequências.<ref name=Marion2004/> No entanto, no presente trabalho, não utilizaremos o formalismo lagrangeano, montando as equações pelos argumentos já mostrados até agora, que envolvem a segunda lei de Newton. Para expressar as soluções gerais, utilizaremos o método de análise de Fourier, poupando-nos de grande parte da álgebra caso-a-caso envolvida em encontrar as autofrequências. | |||
Não é difícil perceber que a segunda equação do sistema (7) tem a forma típica de uma equação de movimento para um oscilador interno (não adjacente às paredes). Desse modo, somando as forças atuantes pela segunda lei de Newton, a generalização das equações para o caso <math>N \geq 3</math> será: | |||
:<math> | :<math> | ||
| Linha 223: | Linha 218: | ||
-kx_{1} - k(x_{1}-x_{2})\text{,} &\quad\text{se} \quad i = 1\\ | -kx_{1} - k(x_{1}-x_{2})\text{,} &\quad\text{se} \quad i = 1\\ | ||
-k(x_{i}-x_{i-1}) - k(x_{i}-x_{i+1}) \text{,} &\quad\text{se} \quad 1<i<N \\ | -k(x_{i}-x_{i-1}) - k(x_{i}-x_{i+1}) \text{,} &\quad\text{se} \quad 1<i<N \\ | ||
-kx_{N} - k(x_{N}-x_{N-1}) \text{,} &\quad\text{se} \quad i = N \quad\quad (11)\\ | -kx_{N} - k(x_{N}-x_{N-1}) \text{,} &\quad\text{se} \quad i = N\text{.} \quad\quad (11)\\ | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
| Linha 232: | Linha 227: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{l}(t) &= \sum_{m=1}^{N}a_{m}^{l}\cos(\omega_{m}t)\text{,} \quad \text{com}\quad l=1\text{,}\,\text{...}\text{,}\,N \quad\\ | x_{l}(t) &= \sum_{m=1}^{N}a_{m}^{l}\cos(\omega_{m}t)\text{,} \quad \text{com}\quad l=1\text{,}\,\text{...}\text{,}\,N\text{.}\quad\\ | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 239: | Linha 234: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{l}(t) &= \sum_{m=1}^{N}c_{m}\sin\left(\frac{lm\pi}{N+1}\right)\cos( | x_{l}(t) &= \sum_{m=1}^{N}c_{m}\sin\left(\frac{lm\pi}{N+1}\right)\cos(\omega_{m}t) \text{, com}\quad l=1\text{,}\,\text{...}\text{,}\,N\text{.} \quad (12)\\ | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 246: | Linha 241: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
x_{l}(t) &= \sqrt{\frac{2}{N+1}}\sum_{m=1}^{N}a_{m}\sin\left(\frac{lm\pi}{N+1}\right)\cos( | x_{l}(t) &= \sqrt{\frac{2}{N+1}}\sum_{m=1}^{N}a_{m}\sin\left(\frac{lm\pi}{N+1}\right)\cos(\omega_{m}t) \text{, com}\quad l=1\text{,}\,\text{...}\text{,}\,N\text{.} \\ | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 259: | Linha 254: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
a_{m} &= \sqrt{\frac{2}{N+1}}\sum_{i=1}^{N}x_{i}\sin\left(\frac{im\pi}{N+1}\right) \text{, com}\quad m=1\text{,}\,\text{...}\text{,}\,N\\ | a_{m} &= \sqrt{\frac{2}{N+1}}\sum_{i=1}^{N}x_{i}\sin\left(\frac{im\pi}{N+1}\right) \text{, com}\quad m=1\text{,}\,\text{...}\text{,}\,N\text{.} \\ | ||
\end{align} \quad (13) | \end{align} \quad (13) | ||
</math> | </math> | ||
| Linha 266: | Linha 261: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
E_{m} &= \frac{1}{2} | E_{m} &= \frac{1}{2}\left(\dot{a}_{m}^{2} + \omega_{m}^2a_{m}^2\right)\text{.} \quad (14) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Através de uma demonstração que pode ser encontrada nas referências<ref name=Lucero2021></ref>, as autofrequências podem ser escritas como: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\omega_{m} &= 2\omega_{0}\sin\left(\frac{m\pi}{2(N+1)}\right) \quad (15) | \omega_{m} &= 2\omega_{0}\sin\left(\frac{m\pi}{2(N+1)}\right)\text{.} \quad (15) | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Todas as expressões mostradas nesta seção são válidas mesmo para o caso de oscilações acopladas não lineares, como é o caso do FPUT.<ref name=Giordano2006></ref> | O argumento do seno sempre se encontra no primeiro quadrante, pois é positivo e é tal que: | ||
:<math>\frac{m\pi}{2(N+1)} < \frac{N\pi}{2(N+1)} < \frac{(N+1)\pi}{2(N+1)} = \frac{\pi}{2}\text{.}</math> | |||
Nota-se, portanto, que as frequências dos modos são sempre menores do que duas vezes a frequência natural (<math>\omega_{m} < 2\omega_{0} = 2\sqrt{k/m}</math>). Todas as expressões mostradas nesta seção são válidas mesmo para o caso de oscilações acopladas não lineares, como é o caso do FPUT.<ref name=Giordano2006></ref> | |||
Podemos comparar, por exemplo, os valores que encontramos para as autofrequências nos casos <math>N=2</math> e <math>N=3</math> com os resultados da equação (15). Seja, por exemplo, <math>k=m=1</math>. Para <math>N=2</math>, pelas expressões (4), <math>\omega_{1} = 1</math> e <math>\omega_{2} = \sqrt{3}</math>, que são os mesmos resultados fornecidos pela equação (15). De modo semelhante, para <math>N=3</math>, pelas expressões (9), <math>\omega_{1} =\sqrt{2-\sqrt{2}}</math>, <math>\omega_{2} = \sqrt{2}</math> e <math>\omega_{3} =\sqrt{2+\sqrt{2}}</math>, que também são os mesmos resultados fornecidos pela equação (15). | Podemos comparar, por exemplo, os valores que encontramos para as autofrequências nos casos <math>N=2</math> e <math>N=3</math> com os resultados da equação (15). Seja, por exemplo, <math>k=m=1</math>. Para <math>N=2</math>, pelas expressões (4), <math>\omega_{1} = 1</math> e <math>\omega_{2} = \sqrt{3}</math>, que são os mesmos resultados fornecidos pela equação (15). De modo semelhante, para <math>N=3</math>, pelas expressões (9), <math>\omega_{1} =\sqrt{2-\sqrt{2}}</math>, <math>\omega_{2} = \sqrt{2}</math> e <math>\omega_{3} =\sqrt{2+\sqrt{2}}</math>, que também são os mesmos resultados fornecidos pela equação (15). | ||
| Linha 292: | Linha 291: | ||
:<math>\ddot{x}_{i} = (x_{i+1} - x_{i}) + (x_{i-1} - x_{i}) + \alpha \left[(x_{i+1} - x_{i})^2 - (x_{i-1} - x_{i})^2 \right]</math> | :<math>\ddot{x}_{i} = (x_{i+1} - x_{i}) + (x_{i-1} - x_{i}) + \alpha \left[(x_{i+1} - x_{i})^2 - (x_{i-1} - x_{i})^2 \right]</math> | ||
Esperava-se teoricamente que, pelo Teorema de Equipartição da Energia, o comportamento desse sistema seria a termalização. Isso significa que, diferentemente dos sistemas lineares, em que, iniciado em um modo, o sistema permanece naquele modo para todo tempo <math>t>0</math> (como podemos perceber nas simulações apresentadas | Esperava-se teoricamente que, pelo Teorema de Equipartição da Energia, o comportamento desse sistema seria a termalização. Isso significa que, diferentemente dos sistemas lineares, em que, iniciado em um modo, o sistema permanece naquele modo para todo tempo <math>t>0</math> (como podemos perceber nas [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Simulações#Osciladores Lineares Acoplados|simulações apresentadas em seguida]], para diversos modos com <math>N=2,\,\text{...},\,5</math>), o sistema tenderia a se tornar uma mistura complicada de '''todos os modos''' a partir de um determinado tempo, e permanecer nesse estado (lembrar que o número de modos depende da quantidade de partículas, <math>N</math>, portanto, no caso <math>N=32</math>, seria esperado que o sistema se tornasse uma mistura de todos os 32 modos após um certo tempo). Uma análise normalmente é feita por meio de gráficos da distribuição de energia entre os modos. A '''Figura 13''', retirada de nossa simulação para <math>N=32</math> do FPUT quadrático unidimensional, ilustra o comportamento do sistema: | ||
<center> | |||
<li style="display: inline-block;">[[Arquivo:Energias_por_modo.png|600px|left|thumb|center|'''Figura 13.''' Esse gráfico corresponde às energias alocadas por modo de vibração em um sistema unidimensional com N=32 partículas do FPUT quadrático, conforme calculado a partir de nossas simulações (ver uma explicação sobre como o gráfico foi feito na seção sobre implementação [[Oscilações_Acopladas/Problema_de_Fermi-Pasta-Ulam-Tsingou#Gráfico_das_energias_do_FPUT_quadrático|numérica]]). Percebe-se claramente o comportamento discutido no parágrafo acima. O sistema inicia no primeiro modo, depois de um tempo passa a uma mistura dos cinco primeiros modos, e por volta de t=10000 retorna quase inteiramente ao primeiro modo de vibração. Ou seja, não houve termalização: a energia não foi distribuída entre os demais modos.]]</li> | |||
</center> | |||
O paradoxo ou problema de FPUT consiste | O comportamento do sistema ilustrado pela '''Figura 13''' corresponde ao que foi observado pelos autores do artigo original.<ref name="FPUToriginal"/> Esse é o caso para baixa amplitude e, consequentemente, baixa energia inicial do sistema (na simulação da '''Figura 13''', a amplitude inicial é igual a 1). Entretanto, caso o sistema possua energia inicial alta, o sistema atinge a termalização. Isso pode ser observado na '''Figura 14''': | ||
<center> | |||
<li style="display: inline-block;">[[Arquivo:termalizacao.png|600px|left|thumb|center|'''Figura 14.''' Esse gráfico corresponde às energias alocadas por modo de vibração em um sistema unidimensional com N=32 partículas do FPUT quadrático, conforme calculado a partir de nossas simulações (ver uma explicação sobre como o gráfico foi feito na seção sobre implementação [[Oscilações_Acopladas/Problema_de_Fermi-Pasta-Ulam-Tsingou#Gráfico_das_energias_do_FPUT_quadrático|numérica]]). Nesse caso, diferentemente da '''Figura 13''', o sistema atinge termalização. Isso ocorre porque a amplitude e a energia inicial do sistema é alta (aqui, a amplitude inicial é igual a 10)]]</li> | |||
</center> | |||
Quando o sistema é linear, a energia total do sistema se reduz a uma soma <math>E=\sum_{k}^{N}E_{k}</math> das energias de cada modo. Essas energias são integrais do movimento, o que leva a <math>E_{k}(t) = E_{k}(0)</math>. Quando há termos não lineares, as energias dos modos normais não são mais integrais do movimento e o Teorema da Equipartição da Energia da mecânica estatística sugere que as médias temporais das energias de cada modo, <math>E_{k}(t)=(1/t)\int_{0}^{t}E_{k}(\tau)d\tau</math>, deveriam tender a um mesmo valor; ou seja, que a energia deveria se distribuir igualmente entre os modos.<ref name=Lucero2021/> | |||
O paradoxo ou problema de FPUT consiste justamente no comportamento de recorrência do sistema e da não termalização.<ref name="FPUToriginal"/><ref name=Lucero2021/> Como pode ser observado nas [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Simulações#FPUT quadrático|simulações]], após um determinado tempo, o sistema volta a uma configuração de modos semelhante à inicial (no nosso caso, o primeiro modo). Note-se que o tempo de recorrência das simulações apresentadas é o mesmo do tempo de recorrência que pode ser visto na '''Figura 13'''. O código está na seção dos [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Programas|programas]]. | |||
== Implementação numérica == | == Implementação numérica == | ||
===Sistemas de equações=== | |||
Vamos explicar nesta seção algumas das características principais dos programas e simulações apresentados neste trabalho. | |||
A implementação dos sistemas de equações dos osciladores lineares é direta e se segue imediatamente da eq. (11), que vamos reproduzir aqui para facilitar a visualização, mas já fazendo <math>m=k=1</math>: | |||
:<math> | :<math> | ||
\ddot{x}_{i} = | |||
\begin{cases} | |||
-x_{1} - (x_{1}-x_{2})\text{,} &\quad\text{se} \quad i = 1\\ | |||
-(x_{i}-x_{i-1}) - (x_{i}-x_{i+1}) \text{,} &\quad\text{se} \quad 1<i<N \\ | |||
-x_{N} - (x_{N}-x_{N-1}) \text{,} &\quad\text{se} \quad i = N \quad\quad \\ | |||
\end{cases} | |||
</math> | |||
A diferença entre esse sistema de equações e o sistema de equações do FPUT quadrático é apenas a inclusão de um termo quadrático. A implementação é trivial após já ter sido implementado o sistema de osciladores lineares. As equações para o FPUT quadrático também já foram [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Adição de Termos Não-Lineares: Problema de FPUT|mostradas na seção anterior]]: | |||
:<math> | |||
\ddot{x}_{i} = | |||
\begin{cases} | \begin{cases} | ||
- | -x_{1} - (x_{1}-x_{2}) + \alpha \left[(x_{2} - x_{1})^2 - x_{1}^2 \right]\text{,} &\quad\text{se} \quad i = 1\\ | ||
- | -(x_{i}-x_{i-1}) - (x_{i}-x_{i+1}) + \alpha \left[(x_{i+1} - x_{i})^2 - (x_{i-1} - x_{i})^2 \right]\text{,} &\quad\text{se} \quad 1<i<N \\ | ||
- | -x_{N} - (x_{N}-x_{N-1}) + \alpha \left[x_{N}^2 - (x_{N-1} - x_{N})^2 \right]\text{,} &\quad\text{se} \quad i = N \quad\quad \\ | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
Esse sistema de equações foi implementado em ambos os códigos [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Programa|disponíveis nesta wiki]]. No caso do programa em Python, está dentro na função acel_quad(), que é chamada pela função velocity_verlet() para integrar as equações do movimento. | |||
===Método de integração=== | |||
O método velocity Verlet também é implementado em ambos os programas. Esse método consiste nas seguintes equações: | |||
:<math> | |||
\begin{align} | |||
x_{i+1} &= x_{i} + v_{i}\Delta t + 0.5a_{i}\Delta t^{2}\\ | |||
a_{i+1} &= f(x_{i+1}) \\ | |||
v_{i+1} &= v_{i} + 0.5(a_{i}+a_{i+1})\Delta t\\ | |||
\end{align} | |||
</math> | |||
Aqui, <math>f</math> é a equação de movimento do sistema. É importante a ordem das equações: devem ser implementadas na ordem acima. Note-se que é necessário guardar o valor anterior da aceleração a cada iteração. Esse método foi implementado para possibilitar a obtenção das velocidades, que são importantes na análise das energias por modo do FPUT. O Verlet seria mais preciso mas não forneceria as velocidades. Como lado negativo, o velocity Verlet tem como característica não conservar plenamente a energia do sistema, que apresenta uma pequena oscilação. Entretanto, para os fins propostos aqui, o método mostrou bons resultados. | |||
===Condições iniciais=== | |||
O programa em C possui como condição inicial apenas posicionar as partículas de modo a garantir que o sistema inicia no primeiro modo. Esse programa implementa o FPUT quadrático com deslocamento vertical, como visto [[Oscilações_Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#FPUT_quadr.C3.A1tico|nessa simulação]]. Note-se que, da equação (12), em <math>t=0</math>: | |||
:<math>\begin{align} | |||
x_{l}(t=0) &= \sum_{m=1}^{N}c_{m}\sin\left(\frac{lm\pi}{N+1}\right) \text{, com}\quad l=1\text{,}\,\text{...}\text{,}\,N\text{.}\\ | |||
\end{align} | |||
</math> | |||
Se queremos iniciar o sistema no primeiro modo, basta fazer <math>m=1</math> na equação acima. De fato, podemos iniciar o sistema em qualquer modo fazendo <math>m=1,\,\text{...},\,N</math> nessa mesma equação. | |||
O programa em Python possui vários tipos diferentes de condições iniciais, porque esse programa (na verdade, conjunto de programas) implementa osciladores lineares acoplados e fput quadrático unidimensionais e bidimensionais tanto em deslocamentos horizontais quanto em deslocamentos verticais da posição de equilíbrio. | |||
A primeira coisa que é inicializada são as posições de equilíbrio de cada partícula. No caso unidimensional, distribuem-se igualmente as posições de equilíbrio das partículas no espaço unidimensional de tamanho L. Depois são calculadas as posições iniciais, de acordo com o modo de oscilação, em relação às posições de equilíbrio. | |||
No caso bidimensional, algo semelhante é feito, mas as posições de equilíbrio das partículas são igualmente espaçadas em um grid quadrado de L x L. O tamanho L é calculado pela função a partir do número de partículas N, que deve ser um quadrado perfeito (N=4, N=9, N=16, N=25, N=49,...). | |||
Foi criada uma função modo_de_osc() que faz a inicialização em qualquer modo. Essa função é chamada pelas funções condicao_inicial_1d() e condicao_inicial_1d_vertical(). | |||
Nos osciladores lineares unidimensionais é usada a função condicao_inicial_1d() que inicializa apenas sistemas unidimensionais com deslocamentos horizontais da posição de equilíbrio. | |||
A função condicao_inicial_1d_vertical() é usada para inicializar o sistema com deslocamentos verticais das posições de equilíbrio. Em específico, usamos apenas para simular o mesmo sistema do programa em C, mas poderia ser usada para qualquer oscilador linear unidimensional também. | |||
A função condicao_inicial_2d() foi usada para a [[Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou#Bidimensional N=49 (Em um grid 7x7)|simulação bidimensional]]. Essa função apenas inicializa o sistema com pequenos deslocamentos randômicos das posições de equilíbrio. | |||
===Gráfico das energias do FPUT quadrático=== | |||
A ideia inicial para construir esse gráfico era usar a ideia sugerida por Lucero et al., 2021<ref name=Lucero2021/> e calcular as amplitudes dos modos por FFT (Fast Fourier Transform). Entretanto, tivemos dificuldades para implementar essa solução. Encontramos uma ótima solução alternativa na wiki de trabalho anterior sobre o [[Problema de Fermi-Pasta-Ulam|FPUT]]. | |||
A ideia consiste no seguinte. Dada as equações (14) e (15), que reproduziremos novamente aqui por clareza: | |||
:<math>\begin{align} | |||
E_{m} &= \frac{1}{2}\left(\dot{a}_{m}^{2} + \omega_{m}^2a_{m}^2\right)\text{.} \quad (14) | |||
\end{align} | |||
</math> | |||
:<math>\begin{align} | |||
\omega_{m} &= 2\omega_{0}\sin\left(\frac{m\pi}{2(N+1)}\right)\text{.} \quad (15) | |||
\end{align} | |||
</math> | |||
Podemos calcular a energia diretamente dessas expressões. Basta notar que, seja um vetor dos modos <math>\vec{n}</math>, definido da seguinte forma: | |||
:<math> | |||
\vec{n} = | |||
\begin{bmatrix} | |||
\sin\left(\frac{m\pi}{(N+1)}\right)\\ | |||
\sin\left(\frac{2m\pi}{(N+1)}\right)\\ | |||
\vdots\\ | |||
\sin\left(\frac{Nm\pi}{(N+1)}\right) \\ | |||
\end{bmatrix} | |||
</math> | |||
e um vetor das posições das partículas do sistema, definido da seguinte forma: | |||
:<math> | |||
\vec{x_{i}} = | |||
\begin{bmatrix} | |||
x_{1} & x_{2} & \cdots & x_{N}\\ | |||
\end{bmatrix} | |||
</math> | |||
As amplitudes dos modos <math>a_{m}</math>, em cada tempo, vão ser dadas pelas projeções das posições nos vetores dos modos <math>\vec{n}</math>, i.e., | |||
:<math> | |||
a_{m} = \sqrt{\frac{2}{N+1}}\vec{x}\cdot{\vec{n}} | |||
</math> | |||
Isso se segue imediatamente da equação (13). Com essas amplitudes e as frequências de cada modo dadas por (15), é simples resolver a parte da energia potencial (<math>\frac{1}{2}\omega_{m}^2a_{m}^2</math>) da equação (14). A parte da energia cinética pode ser resolvida se guardarmos as amplitudes calculadas no tempo anterior e fizermos a seguinte discretização: | |||
:<math> | |||
\frac{da_{m}}{dt} \approx \frac{a_{i}-a_{i-1}}{\Delta t} | |||
</math> | |||
O trabalho [[Problema de Fermi-Pasta-Ulam|anterior]] contém apenas um pequeno erro no cálculo da parte potencial da energia. O código está usando a soma da amplitude no tempo anterior com a amplitude no tempo atual, o que está evidentemente incorreto. O cálculo deve usar apenas a amplitude no tempo atual de cada iteração. | |||
== Simulações == | == Simulações == | ||
| Linha 371: | Linha 489: | ||
=== FPUT quadrático === | === FPUT quadrático === | ||
Abaixo segue uma simulação em que as partículas são deslocadas das posições de equilíbrio verticalmente. Esse modelo é muito interessante para visualizar a propriedade de recorrência ao primeiro modo, embora não seja um modelo muito físico, porque as partículas oscilam apenas na vertical, acopladas às partículas vizinhas. Não há deslocamento na horizontal, e a simulação é na verdade uma simulação unidimensional. | Abaixo segue uma simulação em que as partículas são deslocadas das posições de equilíbrio verticalmente. Esse modelo é muito interessante para visualizar as oscilações das partículas (uma vez que o número de partículas é maior, é mais difícil perceber os padrões de modos nos deslocamentos horizontais). Também é muito útil para visualizar a propriedade de recorrência ao primeiro modo desse sistema não linear, embora não seja um modelo muito físico, porque as partículas oscilam apenas na vertical, acopladas às partículas vizinhas (é como se houvessem molas que conectam cada partícula verticalmente a suas vizinhas, mas sem molas na horizontal). Não há deslocamento na horizontal, e a simulação é na verdade uma simulação unidimensional. Atentar que nessas simulações há apenas 30 partículas oscilando de fato. Duas estão presas nas paredes. | ||
Parâmetros da simulação | Parâmetros da simulação da '''Figura 14''' e da '''Figura 15''': <math>k = 1.0, m = 1.0, \alpha = 0.25, \Delta t = 0.01, L = 20.0, N = 32, amplitude=1</math>. | ||
<gallery class="center" mode=packed heights=250px> | <gallery class="center" mode=packed heights=250px> | ||
fput_deslocamento_vertical_parte1.gif|'''Figura | fput_deslocamento_vertical_parte1.gif|'''Figura 14.''' Primeira parte da simulação do oscilador acoplado com N=32 partículas com deslocamento limitado à vertical. Essa simulação mostra que o sistema foi inicializado no modo 1. Já podemos perceber, no final da simulação, que o sistema começa a sair do modo 1 e entrar em uma mistura de modos. | ||
fput_deslocamento_vertical_parte2.gif|'''Figura | fput_deslocamento_vertical_parte2.gif|'''Figura 15.''' Segunda parte da simulação do oscilador acoplado com N=32 partículas com deslocamento limitado à vertical. Nessa simulação é possível perceber a recorrência do primeiro modo de oscilação. Após ter oscilado por um tempo considerável com uma mistura de modos, o sistema retorna ao modo inicial. | ||
</gallery> | </gallery> | ||
== | == Programas == | ||
* [[Código em C e scripts para FPUT com deslocamento vertical]] | * [[Código em C e scripts para FPUT com deslocamento vertical]] | ||
| Linha 393: | Linha 510: | ||
== Bibliografia principal == | == Bibliografia principal == | ||
* Marion, J.B., Thornton, S.T. "Classical Dynamics of Particles and Systems". Thomson Learning, Belmont, 2004. | * Marion, J.B., Thornton, S.T. "Classical Dynamics of Particles and Systems". 5th Edition. Thomson Learning, Belmont, 2004. | ||
* Giordano, N.J., Nakanishi, H. "Computational Physics". 2nd Edition. Prentice Hall, Upper Saddle River, 2006. | * Giordano, N.J., Nakanishi, H. "Computational Physics". 2nd Edition. Prentice Hall, Upper Saddle River, 2006. | ||
Edição atual tal como às 23h43min de 8 de maio de 2022
Grupo: Paula Pandolfo, Ramiro de Souza, Samuel Dieterich e Wallace Carvalho
Objetivo: Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas as análises de resultados serão restritas aos casos unidimensionais, por simplicidade.
Introdução
Os osciladores talvez sejam os sistemas mais estudados em toda a Física, sendo capazes de modelar uma ampla gama de fenômenos, como, p. ex., pêndulos, circuitos eletrônicos e interações moleculares. O comportamento linear desse tipo de sistema, em particular, possui resultados analíticos bem conhecidos, facilitando o tratamento matemático de sistemas complexos que possam ser modelados por conjuntos de osciladores.
O problema de FPUT (Enrico Fermi, John R. Pasta, Stanislaw M. Ulam, Mary Tsingou) resulta da análise computacional de um sistema de partículas que apenas interagem com seus vizinhos, com interações modeladas por oscilações acopladas com a adição de um termo não-linear, que pode ser quadrático ou cúbico. O intuito original da simulação era estudar como tal sistema evolui para o equilíbrio térmico. Se as forças envolvidas forem estritamente lineares, a energia alocada em cada modo de vibração não se distribui entre os demais modos, e o sistema nunca atinge o equilíbrio térmico. Adicionando termos não lineares, supunha-se que, pelo Teorema da Equipartição da Energia, a energia total do sistema seria distribuída uniformemente entre os modos normais de vibração após um certo tempo, resultando no equilíbrio térmico do sistema. Entretanto, isso não foi observado nas simulações computacionais.
O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo [1], que relataram o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).[2]
A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores lineares acoplados. Em seguida, compararemos esses resultados com simulações computacionais, a fim de exemplificar visualmente seu significado. Após apresentar as fundações teóricas desses casos mais simples em que as forças são lineares, trataremos do problema de FPUT em si, examinando a situação em que a interação não-linear se dá através de um termo quadrático nas coordenadas generalizadas utilizadas. Tal tratamento tem de ser majoritariamente computacional, já que as equações diferenciais envolvidas não são, em geral, fáceis de se resolver analiticamente.
Osciladores Lineares Acoplados
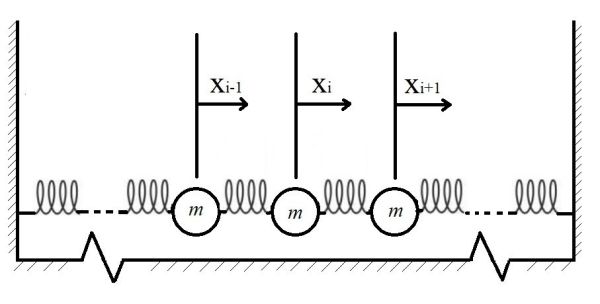
Um modelo geral de sistema unidimensional de osciladores lineares acoplados é ilustrado pela Figura 1.
Cada partícula possui duas vizinhas com as quais interage por meio das molas, exceto as partículas localizadas nos extremos da cadeia, que possuem apenas uma partícula vizinha cada. As interações das partículas dos extremos das cadeias se restringem, portanto, à interação com uma vizinha e com uma mola conectada a uma das paredes externas à cadeia. Como este problema é unidimensional, a posição de cada partícula pode ser descrita por apenas um grau de liberdade. Vamos escolher os deslocamentos em relação à respectiva posição de equilíbrio da partícula como nossas coordenadas generalizadas, definindo como positivos os deslocamentos para a direita e negativos para a esquerda. No total, um sistema com partículas terá, portanto, graus de liberdade. Vamos tratar aqui o caso em que as forças das molas são lineares, seguindo a lei de Hooke; i.e., forças dadas pela forma . Além disso, para simplificar e minimizar o número de parâmetros das simulações, vamos considerar que, em todos os casos mostrados, todas as molas possuem as mesmas constantes de acoplamento linear e todas as partículas possuem as mesmas massas .
N=2
Nota: O conteúdo abaixo segue aproximadamente a seção 12.2 de Marion e Thornton (2004).[3] Entretanto, há diversas modificações e inclusões. Por exemplo, na descrição das equações de movimento e nas definições dos modos normais.
Para nos familiarizarmos com este sistema, consideremos inicialmente o caso do oscilador linear acoplado mais simples, com apenas duas partículas (), cada uma com massa , e três molas com os mesmos valores de constantes, .
Utilizando a segunda lei de Newton, mostra-se que as equações de movimento do sistema são:
Uma forma direta de se montar as equações de movimento de um sistema acoplado é pensar em termos dos deslocamentos em relação às posições de equilíbrio (, com , no sistema considerado aqui). Por exemplo, na primeira das equações acima, a partícula 1 está sujeita à força elástica da mola conectada à parede (termo ) e à força da mola conectada à partícula 2 (termo ). Esse último termo é definido conforme o seguinte: caso a mola que está conectada às partículas 1 e 2 esteja comprimida, deve ser maior que e a partícula 1 estará sofrendo uma força que é contrária à compressão, ou seja, com sinal negativo. De modo semelhante para a partícula 2, mas nesse caso, devido à posição ocupada pela partícula 2 na cadeia, com maior que , o sentido da força contrária à compressão tem sinal positivo, manifestando a terceira lei de Newton.
Uma dificuldade imposta pelo sistema (1) é o fato das equações serem acopladas, que a aceleração da partícula 1 depende da posição da partícula 2, e vice-versa. Vamos supor que esse sistema de equações tenha soluções na seguinte forma:
onde e são constantes e é uma frequência angular ainda indeterminada. Essa suposição é fisicamente justificável: sabemos que as soluções são oscilatórias, e exponenciais imaginárias podem ser escritas em termos de senos e cossenos pela fórmula de Euler. Se substituirmos as expressões em (2) na equação (1) e rearranjarmos os termos, obteremos:
Ou, eliminando as exponenciais e reagrupando termos:
O sistema de equações (3) apenas terá soluções não triviais se o determinante da matriz dos coeficientes que acompanham os for igual a zero, i.e.:
O resultado desse determinante ser igual a zero é uma equação quadrática simples em , sendo as soluções facilmente obtidas. Como para cada solução existe uma solução , apresentaremos apenas o módulo das frequências:
e são então denominadas as frequências características ou autofrequências do sistema. As soluções mais gerais do sistema de equações diferenciais lineares (1) vão ser então combinações lineares das soluções (2) com as frequências dadas por (4):
Nota-se que cada uma das soluções é uma superposição (em geral) complicada que envolve as duas autofrequências. Isso é uma consequência direta do acoplamento presente no sistema (1). Para eliminar este acoplamento, vamos definir novas variáveis: e , ou
Substituindo essas expressões no sistema de equações (1), ficamos com:
Se somarmos as duas equações acima, e se subtrairmos a segunda da primeira, obtemos, respectivamente:
Reconhecemos imediatamente as equações acima como equações de osciladores harmônicos simples, desacopladas e, portanto, com soluções independentes. As soluções são dadas por
e são chamadas de coordenadas normais. Por definição, são coordenadas que desacoplam as equações diferenciais do sistema e possuem soluções com frequências únicas, bem definidas. Sempre podem ser escritas como algum tipo de combinação linear das coordenadas originais. De modo semelhante, as coordenadas usuais do sistema sempre podem ser escritas como combinações lineares das coordenadas normais. No caso geral, para mais partículas, a combinação linear dos deslocamentos que produz as coordenadas normais é trabalhosa de se encontrar. Note-se que, no caso de duas partículas, é simples encontrá-las meramente por inspeção. Se impusermos as condições iniciais e , e as constantes e vão ser iguais a zero, o que implica , para todo . Esse primeiro modo normal corresponderá a uma oscilação simétrica, em que as duas partículas oscilarão em fase, com frequência . De modo semelhante, se impusermos as condições iniciais e , , para todo , e as partículas oscilarão fora de fase, com frequência . Pelas expressões dadas em (4) e pelas simulações abaixo, destaca-se que a frequência associada ao modo simétrico é menor do que a frequência do modo antissimétrico. Esse é um resultado geral de oscilações acopladas: quanto maior o grau de simetria da oscilação, menor o valor da frequência.[3]
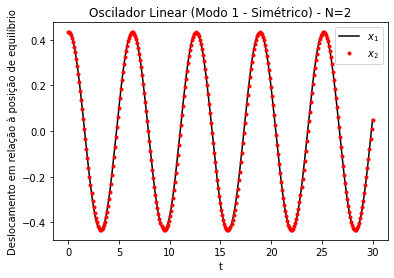
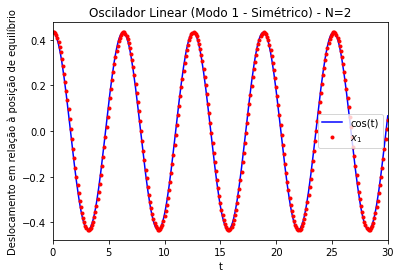
Alguns resultados das simulações para os modos desse caso podem ser observados na Figura 2 e na Figura 3. Fica evidente a menor frequência do modo simétrico em relação ao modo antissimétrico. Além disso, podemos observar a concordância com os valores teóricos encontrados para as frequências: e . O modo simétrico consiste em uma oscilação em que as partículas estão em fase; no modo antissimétrico, as partículas oscilam fora de fase.
Figura 2. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta no gráfico, partícula da esquerda na simulação ao lado) e 2 (pontos vermelhos no gráfico, partícula da direita na simulação ao lado). k=m=1. Amplitude inicial de ~0.433. N=2
Figura 3.Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta, partícula da esquerda na simulação ao lado) e 2 (pontos vermelhos, partícula da direita na simulação ao lado). k=m=1. Amplitude inicial de ~0.433. N=2
A concordância das frequências com os valores teóricos calculados pode ser vista na Figura 4 e na Figura 5. Podemos observar a concordância com os valores teóricos encontrados para as frequências: e .
Figura 4. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1 (esquerda na simulação acima), conforme integração numérica (pontos vermelhos), em relação ao valor teórico (linha azul). k=m=1. Amplitude inicial de ~0.433. N=2
Figura 5. Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1 (esquerda na simulação acima), conforme integração numérica (pontos vermelhos), em relação ao valor teórico (linha azul). Amplitude inicial de ~0.433. k=m=1. Amplitude inicial de ~0.433. N=2
N=3
Seguindo a mesma lógica apresentada para partículas, podemos montar as equações de movimento do sistema com partículas. A única diferença é que a partícula central apenas está conectada a partículas vizinhas, não estando conectada a paredes externas:
Novamente, supomos soluções do tipo
Substituindo (8) em (7) e seguindo os mesmos passos feitos para partículas, obteremos o sistema linear para os :
O sistema de equações acima apenas terá soluções não triviais se o determinante dos coeficientes dos for igual a zero. Portanto:
A equação resultante é . Simples de ser resolvida analiticamente por fatoração, esta equação tem as soluções de módulo:
Note-se que aqui já não é mais tão simples identificar as coordenadas normais. Além disso, embora tenha sido simples até aqui obter as autofrequências, o processo é tedioso e a equação característica se torna cada vez mais difícl de se resolver analiticamente.
Podemos escrever as soluções da seguinte forma, de modo semelhante a como fizemos para :
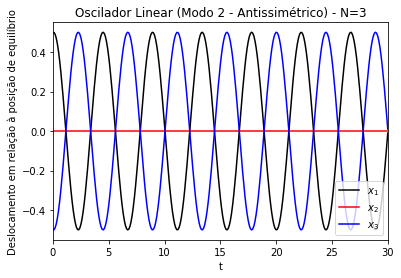
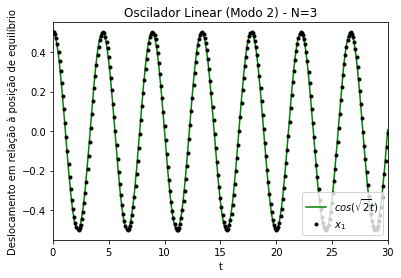
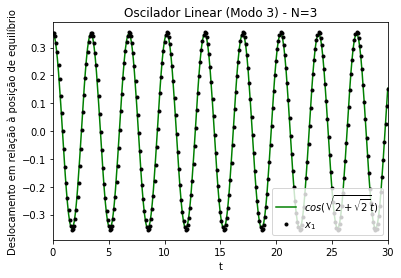
Alguns resultados das simulações para os modos desse caso podem ser observados na Figura 6, na Figura 7 e na Figura 8. Nota-se, mais uma vez, que a menor frequência em relação aos demais modos é aquela associada ao modo simétrico. O modo simétrico consiste em uma oscilação em que todas as partículas estão em fase; no modo antissimétrico, as partículas 1 e 3 oscilam fora de fase, a 2 permanece parada. A novidade em relação ao caso de é o surgimento de um novo modo, o modo 3, em que as partículas 1 e 3 oscilam em fase, e a partícula 2 oscila fora de fase em relação às partículas 1 e 3.
Figura 6. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta), 2 (linha vermelha) e 3 (pontos azuis). k=m=1. Amplitude inicial de ~ 0.35 para as partículas 1 e 3, e ~0.5 para a partícula 2. N=3
Figura 8. Modo de oscilação 3 de um oscilador linear acoplado unidimensional. Gráficos dos deslocamentos (x) em relação à posição de equilíbrio das partículas 1 (linha preta), 2 (linha vermelha) e 3 (pontos azuis). k=m=1. Amplitude inicial de ~ 0.35 para as partículas 1 e 3, e ~0.5 para a partícula 2. N=3
A concordância das frequências com os valores teóricos calculados pode ser vista na Figura 9, na Figura 10 e na Figura 11. Podemos observar a concordância com os valores teóricos encontrados para as frequências: , e .
Figura 9. Modo de oscilação simétrico (modo 1) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.35. N=3
Figura 10. Modo de oscilação antissimétrico (modo 2) de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.5. N=3
Figura 11. Modo de oscilação 3 de um oscilador linear acoplado unidimensional. Comparação entre os gráficos dos deslocamentos (x) em relação à posição de equilíbrio da partículas 1, conforme integração numérica (pontos pretos), em relação ao valor teórico (linha verde). k=m=1. Amplitude inicial de ~ 0.35. N=3
Caso geral
O formalismo lagrangeano fornece uma técnica poderosa para construir as equações de movimento para o caso geral de partículas, bem como para facilitar o cálculo das coordenadas normais e das autofrequências.[3] No entanto, no presente trabalho, não utilizaremos o formalismo lagrangeano, montando as equações pelos argumentos já mostrados até agora, que envolvem a segunda lei de Newton. Para expressar as soluções gerais, utilizaremos o método de análise de Fourier, poupando-nos de grande parte da álgebra caso-a-caso envolvida em encontrar as autofrequências.
Não é difícil perceber que a segunda equação do sistema (7) tem a forma típica de uma equação de movimento para um oscilador interno (não adjacente às paredes). Desse modo, somando as forças atuantes pela segunda lei de Newton, a generalização das equações para o caso será:
O conjunto de equações (11) vai ser importante para a implementação numérica.
As soluções (5) e (10) apresentam um padrão. Se tomarmos apenas as partes reais das soluções, podemos redefinir as constantes duas a duas e escrever a solução geral como:
As constantes são chamadas de amplitudes dos modos normais e indicam o quanto de cada modo normal, de frequência bem definida, está presente na solução de cada . É possível mostrar (o que não faremos aqui por razões de tempo e espaço, mas pode ser consultado nas referências [4]) que, usando condições de contorno , as soluções podem ser reescritas como
É comum na literatura[5] redefinir a constante da seguinte forma:
A qualquer instante de tempo, os deslocamentos das partículas em relação às posições de equilíbrio podem ser escritos como uma soma de modos normais. Esses modos normais são ondas estacionárias. Ver, por exemplo, a Figura 12, com os cinco primeiros modos.
É possível, portanto, por uma transformada inversa, escrever
As energias de cada modo podem ser escritas como (com representando a amplitude da velocidade do modo):
Através de uma demonstração que pode ser encontrada nas referências[4], as autofrequências podem ser escritas como:
O argumento do seno sempre se encontra no primeiro quadrante, pois é positivo e é tal que:
Nota-se, portanto, que as frequências dos modos são sempre menores do que duas vezes a frequência natural (). Todas as expressões mostradas nesta seção são válidas mesmo para o caso de oscilações acopladas não lineares, como é o caso do FPUT.[5]
Podemos comparar, por exemplo, os valores que encontramos para as autofrequências nos casos e com os resultados da equação (15). Seja, por exemplo, . Para , pelas expressões (4), e , que são os mesmos resultados fornecidos pela equação (15). De modo semelhante, para , pelas expressões (9), , e , que também são os mesmos resultados fornecidos pela equação (15).
Adição de Termos Não-Lineares: Problema de FPUT
Como já discutido, se as forças em um sistema de osciladores acoplados forem todas da forma da lei de Hooke, o sistema jamais alcançará o equilíbrio térmico, pois os modos têm independência linear entre si. Para fazer isso, temos de acrescentar termos não-lineares de interação. Vamos tratar aqui o primeiro caso estudado no artigo original,[1] em que os termos não-lineares são quadráticos nas coordenadas .
Para os osciladores internos, teremos então a seguinte equação de movimento:
Nessa equação, a constante faz o papel da constante das molas apresentada anteriormente para o caso puramente linear, enquanto informa a intensidade da força não-linear. É importante ressaltar que nem todos os autores definem os termos quadráticos dessa forma. Atualmente é mais comum ver esses termos definidos como faz, por exemplo, Lucero et al., 2021[4], que usa o sinal positivo entre os termos quadráticos, no interior dos colchetes. Podemos isolar a aceleração nesta equação; vamos escolher e definir . A equação fica então:
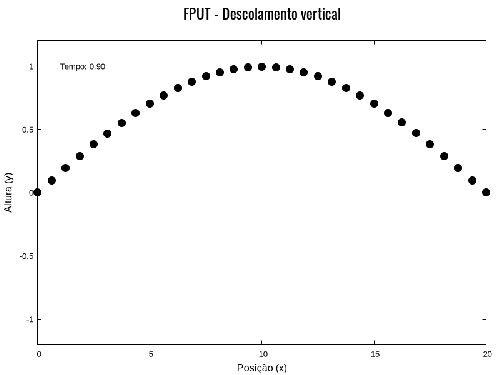
Esperava-se teoricamente que, pelo Teorema de Equipartição da Energia, o comportamento desse sistema seria a termalização. Isso significa que, diferentemente dos sistemas lineares, em que, iniciado em um modo, o sistema permanece naquele modo para todo tempo (como podemos perceber nas simulações apresentadas em seguida, para diversos modos com ), o sistema tenderia a se tornar uma mistura complicada de todos os modos a partir de um determinado tempo, e permanecer nesse estado (lembrar que o número de modos depende da quantidade de partículas, , portanto, no caso , seria esperado que o sistema se tornasse uma mistura de todos os 32 modos após um certo tempo). Uma análise normalmente é feita por meio de gráficos da distribuição de energia entre os modos. A Figura 13, retirada de nossa simulação para do FPUT quadrático unidimensional, ilustra o comportamento do sistema:

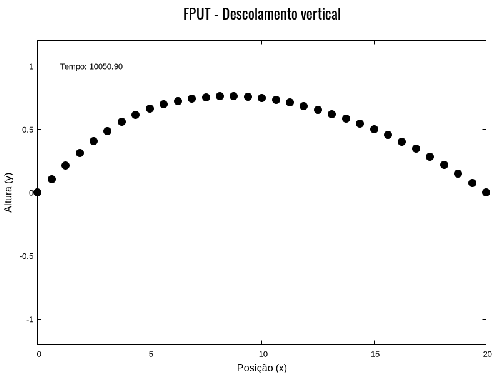
O comportamento do sistema ilustrado pela Figura 13 corresponde ao que foi observado pelos autores do artigo original.[1] Esse é o caso para baixa amplitude e, consequentemente, baixa energia inicial do sistema (na simulação da Figura 13, a amplitude inicial é igual a 1). Entretanto, caso o sistema possua energia inicial alta, o sistema atinge a termalização. Isso pode ser observado na Figura 14:

Quando o sistema é linear, a energia total do sistema se reduz a uma soma das energias de cada modo. Essas energias são integrais do movimento, o que leva a . Quando há termos não lineares, as energias dos modos normais não são mais integrais do movimento e o Teorema da Equipartição da Energia da mecânica estatística sugere que as médias temporais das energias de cada modo, , deveriam tender a um mesmo valor; ou seja, que a energia deveria se distribuir igualmente entre os modos.[4]
O paradoxo ou problema de FPUT consiste justamente no comportamento de recorrência do sistema e da não termalização.[1][4] Como pode ser observado nas simulações, após um determinado tempo, o sistema volta a uma configuração de modos semelhante à inicial (no nosso caso, o primeiro modo). Note-se que o tempo de recorrência das simulações apresentadas é o mesmo do tempo de recorrência que pode ser visto na Figura 13. O código está na seção dos programas.
Implementação numérica
Sistemas de equações
Vamos explicar nesta seção algumas das características principais dos programas e simulações apresentados neste trabalho.
A implementação dos sistemas de equações dos osciladores lineares é direta e se segue imediatamente da eq. (11), que vamos reproduzir aqui para facilitar a visualização, mas já fazendo :
A diferença entre esse sistema de equações e o sistema de equações do FPUT quadrático é apenas a inclusão de um termo quadrático. A implementação é trivial após já ter sido implementado o sistema de osciladores lineares. As equações para o FPUT quadrático também já foram mostradas na seção anterior:
Esse sistema de equações foi implementado em ambos os códigos disponíveis nesta wiki. No caso do programa em Python, está dentro na função acel_quad(), que é chamada pela função velocity_verlet() para integrar as equações do movimento.
Método de integração
O método velocity Verlet também é implementado em ambos os programas. Esse método consiste nas seguintes equações:
Aqui, é a equação de movimento do sistema. É importante a ordem das equações: devem ser implementadas na ordem acima. Note-se que é necessário guardar o valor anterior da aceleração a cada iteração. Esse método foi implementado para possibilitar a obtenção das velocidades, que são importantes na análise das energias por modo do FPUT. O Verlet seria mais preciso mas não forneceria as velocidades. Como lado negativo, o velocity Verlet tem como característica não conservar plenamente a energia do sistema, que apresenta uma pequena oscilação. Entretanto, para os fins propostos aqui, o método mostrou bons resultados.
Condições iniciais
O programa em C possui como condição inicial apenas posicionar as partículas de modo a garantir que o sistema inicia no primeiro modo. Esse programa implementa o FPUT quadrático com deslocamento vertical, como visto nessa simulação. Note-se que, da equação (12), em :
Se queremos iniciar o sistema no primeiro modo, basta fazer na equação acima. De fato, podemos iniciar o sistema em qualquer modo fazendo nessa mesma equação.
O programa em Python possui vários tipos diferentes de condições iniciais, porque esse programa (na verdade, conjunto de programas) implementa osciladores lineares acoplados e fput quadrático unidimensionais e bidimensionais tanto em deslocamentos horizontais quanto em deslocamentos verticais da posição de equilíbrio.
A primeira coisa que é inicializada são as posições de equilíbrio de cada partícula. No caso unidimensional, distribuem-se igualmente as posições de equilíbrio das partículas no espaço unidimensional de tamanho L. Depois são calculadas as posições iniciais, de acordo com o modo de oscilação, em relação às posições de equilíbrio.
No caso bidimensional, algo semelhante é feito, mas as posições de equilíbrio das partículas são igualmente espaçadas em um grid quadrado de L x L. O tamanho L é calculado pela função a partir do número de partículas N, que deve ser um quadrado perfeito (N=4, N=9, N=16, N=25, N=49,...).
Foi criada uma função modo_de_osc() que faz a inicialização em qualquer modo. Essa função é chamada pelas funções condicao_inicial_1d() e condicao_inicial_1d_vertical().
Nos osciladores lineares unidimensionais é usada a função condicao_inicial_1d() que inicializa apenas sistemas unidimensionais com deslocamentos horizontais da posição de equilíbrio.
A função condicao_inicial_1d_vertical() é usada para inicializar o sistema com deslocamentos verticais das posições de equilíbrio. Em específico, usamos apenas para simular o mesmo sistema do programa em C, mas poderia ser usada para qualquer oscilador linear unidimensional também.
A função condicao_inicial_2d() foi usada para a simulação bidimensional. Essa função apenas inicializa o sistema com pequenos deslocamentos randômicos das posições de equilíbrio.
Gráfico das energias do FPUT quadrático
A ideia inicial para construir esse gráfico era usar a ideia sugerida por Lucero et al., 2021[4] e calcular as amplitudes dos modos por FFT (Fast Fourier Transform). Entretanto, tivemos dificuldades para implementar essa solução. Encontramos uma ótima solução alternativa na wiki de trabalho anterior sobre o FPUT.
A ideia consiste no seguinte. Dada as equações (14) e (15), que reproduziremos novamente aqui por clareza:
Podemos calcular a energia diretamente dessas expressões. Basta notar que, seja um vetor dos modos , definido da seguinte forma:
e um vetor das posições das partículas do sistema, definido da seguinte forma:
As amplitudes dos modos , em cada tempo, vão ser dadas pelas projeções das posições nos vetores dos modos , i.e.,
Isso se segue imediatamente da equação (13). Com essas amplitudes e as frequências de cada modo dadas por (15), é simples resolver a parte da energia potencial () da equação (14). A parte da energia cinética pode ser resolvida se guardarmos as amplitudes calculadas no tempo anterior e fizermos a seguinte discretização:
O trabalho anterior contém apenas um pequeno erro no cálculo da parte potencial da energia. O código está usando a soma da amplitude no tempo anterior com a amplitude no tempo atual, o que está evidentemente incorreto. O cálculo deve usar apenas a amplitude no tempo atual de cada iteração.
Simulações
Osciladores Lineares Acoplados
N=2
N=3
N=4
Embora não tenhamos feito análises para os casos de N=4 e N=5 partículas, abaixo seguem simulações dos modos desses osciladores acoplados lineares unidimensionais. Observa-se o mesmo padrão de aumento da frequência com o número do modo. O modo simétrico sempre apresenta menor frequência.
N=5
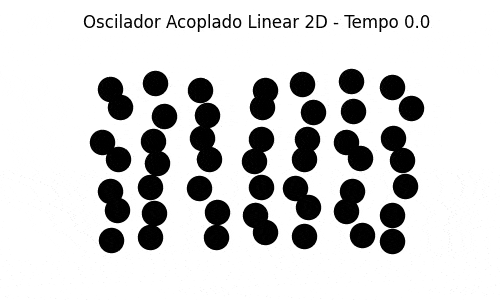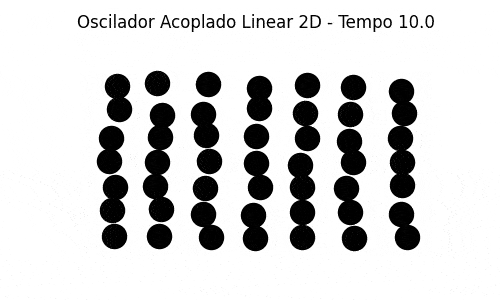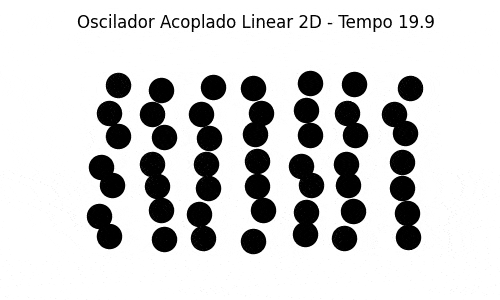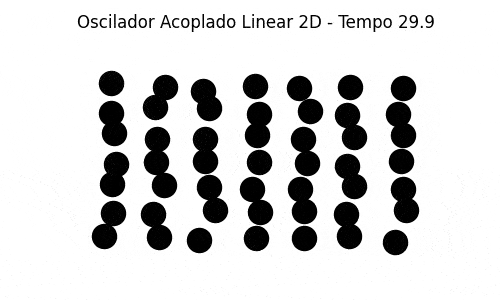
Bidimensional N=49 (Em um grid 7x7)
Também implementamos uma simulação bidimensional de massas acopladas com as partículas vizinhas de cima, de baixo e dos lados. As partículas das fronteiras estão conectadas às paredes (em cima, embaixo e dos lados). A generalização do caso unidimensional é direta e foi razoavelmente simples de se implementar, uma vez estabelecida a condição inicial (colocar as partículas nas posições de equilíbrio, espaçadas igualmente em um grid, e deslocar randomicamente cada uma de sua posição de equilíbrio por um valor bem pequeno). A simulação mostra um comportamento que pode ser associado à dinâmica molecular.
FPUT quadrático
Abaixo segue uma simulação em que as partículas são deslocadas das posições de equilíbrio verticalmente. Esse modelo é muito interessante para visualizar as oscilações das partículas (uma vez que o número de partículas é maior, é mais difícil perceber os padrões de modos nos deslocamentos horizontais). Também é muito útil para visualizar a propriedade de recorrência ao primeiro modo desse sistema não linear, embora não seja um modelo muito físico, porque as partículas oscilam apenas na vertical, acopladas às partículas vizinhas (é como se houvessem molas que conectam cada partícula verticalmente a suas vizinhas, mas sem molas na horizontal). Não há deslocamento na horizontal, e a simulação é na verdade uma simulação unidimensional. Atentar que nessas simulações há apenas 30 partículas oscilando de fato. Duas estão presas nas paredes.
Parâmetros da simulação da Figura 14 e da Figura 15: .
Figura 15. Segunda parte da simulação do oscilador acoplado com N=32 partículas com deslocamento limitado à vertical. Nessa simulação é possível perceber a recorrência do primeiro modo de oscilação. Após ter oscilado por um tempo considerável com uma mistura de modos, o sistema retorna ao modo inicial.
Programas
Referências
- ↑ 1,0 1,1 1,2 1,3 Fermi, E.; Pasta, J.; Ulam, S. (1955). "Studies of Nonlinear Problems" (PDF). Document LA-1940. Los Alamos National Laboratory. [Acessado 02 Maio 2022]. [1]
- ↑ Grant, V. "We Thank Miss Mary Tsingou", National Security Science. Winter 2020: pp. 36-43. [Acessado 02 Maio 2022]. [2]
- ↑ 3,0 3,1 3,2 Marion e Thornton, pp. 469-473
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 Lucero, Davi de Mello e Pinheiro Moreira, Pedro Augusto Franco. "O problema Fermi-Pasta-Ulam-Tsingou: Equiparticão de energia vista através de simulações computacionais". Revista Brasileira de Ensino de Física [online]. 2021, v. 43 [Acessado 1 Maio 2022]. [3]
- ↑ 5,0 5,1 Giordano e Nakanishi, pp. 296-297
Bibliografia principal
- Marion, J.B., Thornton, S.T. "Classical Dynamics of Particles and Systems". 5th Edition. Thomson Learning, Belmont, 2004.
- Giordano, N.J., Nakanishi, H. "Computational Physics". 2nd Edition. Prentice Hall, Upper Saddle River, 2006.


















































































![{\displaystyle m{\ddot {x}}_{i}=k_{1}\left[(x_{i+1}-x_{i})+(x_{i-1}-x_{i})\right]+k_{2}\left[(x_{i+1}-x_{i})^{2}-(x_{i-1}-x_{i})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9436bce744045d6051917ac83a069f3453428e85)





![{\displaystyle {\ddot {x}}_{i}=(x_{i+1}-x_{i})+(x_{i-1}-x_{i})+\alpha \left[(x_{i+1}-x_{i})^{2}-(x_{i-1}-x_{i})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eddc4b4cf04f8980dc32f7c1be867689c1835d61)








![{\displaystyle {\ddot {x}}_{i}={\begin{cases}-x_{1}-(x_{1}-x_{2})+\alpha \left[(x_{2}-x_{1})^{2}-x_{1}^{2}\right]{\text{,}}&\quad {\text{se}}\quad i=1\\-(x_{i}-x_{i-1})-(x_{i}-x_{i+1})+\alpha \left[(x_{i+1}-x_{i})^{2}-(x_{i-1}-x_{i})^{2}\right]{\text{,}}&\quad {\text{se}}\quad 1<i<N\\-x_{N}-(x_{N}-x_{N-1})+\alpha \left[x_{N}^{2}-(x_{N-1}-x_{N})^{2}\right]{\text{,}}&\quad {\text{se}}\quad i=N\quad \quad \\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03602d0c5c213808f48496a23978a45a1e9c31b7)