Algoritmo de Wang-Landau: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 41: | Linha 41: | ||
Quando o histograma é considerado reto, pelas condições descritas acima, reduzimos o valor de <math> f </math> de forma que o novo valor será <math> f_1 = f_0/2 </math>, resetamos o histograma <math> H(E) </math> e recomeçamos o passeio aleatório. | Quando o histograma é considerado reto, pelas condições descritas acima, reduzimos o valor de <math> f </math> de forma que o novo valor será <math> f_1 = f_0/2 </math>, resetamos o histograma <math> H(E) </math> e recomeçamos o passeio aleatório. | ||
A simulação é parada para um valor de <math> f </math> predeterminado. No caso, usamos <math> f_{final} = \exp (10^{-8} = 1.00000001 </math>. | A simulação é parada para um valor de <math> f </math> predeterminado. No caso, usamos <math> f_{final} = \exp (10^{-8}) = 1.00000001 </math>. | ||
==Aplicação ao Modelo de Ising 2D== | |||
===Modelo de Ising=== | |||
O modelo de Ising é uma rede 2D, de tamanho <math> L \times L </math> que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo<ref name=ising> A. Rosa, C. Pires, L. Doria, Ising 2D, Wikia da Física Computacional da UFRGS. https://fiscomp.if.ufrgs.br/index.php/Ising_2D#Modelo_de_Ising </ref> Cada sítio pode ter o valor de spin <math>+1</math> ou <math>-1</math>. | |||
O hamiltoniano de interação pode ser calculado por <math> \mathcal{H} = -\sum_{\langle i,j \rangle}\sigma_i \sigma_j </math> onde <math> \langle i,j </math> indica pares distintos de vizinhos-mais-próximos. | |||
====Algoritmo==== | ====Algoritmo==== | ||
Resumindo, o passo a passo do algoritmo pode ser escrito como: | Resumindo, o passo a passo do algoritmo pode ser escrito como: | ||
1. | 1. Defino <math>g(E) = 1</math> para todos <math> E </math> e o fator de modificação inicial <math>f_0 = e</math>; | ||
2. Aleatoriamente, | 2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade <math> p(E_1 \to E_2) = min(g(E_1)/g(E_2), 1) </math>; | ||
3. Modifico a densidade de estados <math> g(E) \to g(E) \times f </math> e atualizo o histograma <math>H(E)</math>; | 3. Modifico a densidade de estados <math> g(E) \to g(E) \times f </math> e atualizo o histograma <math>H(E)</math>; | ||
4. Continuo até o histograma estar reto, então diminuo o valor de <math>f</math> e reseto o | 4. Continuo até o histograma estar reto, então diminuo o valor de <math>\ln f</math> pela metade e reseto o histograma <math>H(E)</math>; | ||
5. Repito 2-4 até <math> | 5. Repito os passos 2-4 até <math> f < 1.00000001 </math>. | ||
== | ====Implementação==== | ||
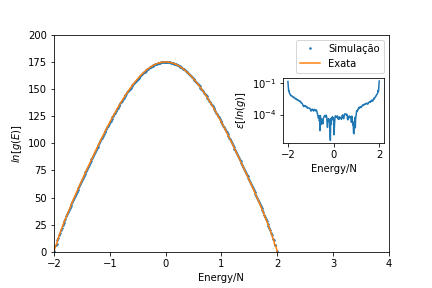
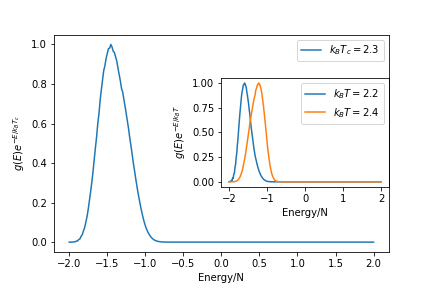
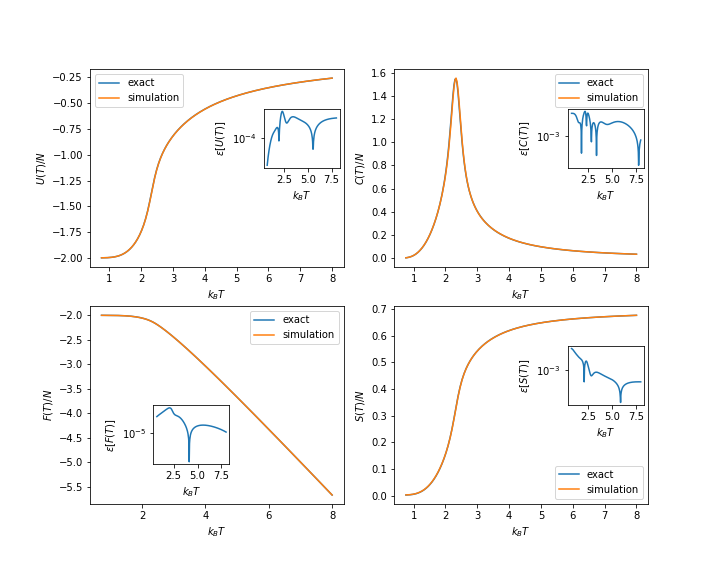
====Resultados==== | ====Resultados==== | ||
Edição das 20h53min de 28 de novembro de 2021
Nomes: Rafael Abel da Silveira e William Machado Pantaleão
Introdução
Simulações computacionais, como o método de Monte Carlo, são vastamente utilizadas para estudar transições de fase e fenômenos críticos. O método padrão para simulações de Monte Carlo é o algoritmo de Metropolis, entretanto, algoritmos novos e mais eficientes são usados em simulações modernas, como o algoritmo de Wang-Landau. Ao contrário dos métodos convencionais de Monte Carlo, que geram diretamente uma distribuição canônica a uma dada temperatura , a abordagem de Wang-Landau estima a densidade de estados diretamente por meio de um passeio aleatório, que produz um histograma plano no espaço de energia . [1]
Mesmo para modelos que podem ser resolvidos analiticamente, a densidade de estados não pode ser determinada para sistemas maiores [2]. Com o algoritmo de Wang-Landau, é possível obter a a partir de um passeio aleatório. A estimativa para é melhorada a cada etapa do passeio aleatório, usando um fator de modificação cuidadosamente controlado, para produzir um resultado que converge para o valor real rapidamente.
Amostragem de Wang-Landau
No início da simulação, é desconhecido e fazemos uma estimativa inicial para ele. A abordagem mais simples é definir para todas as energias possíveis . A configuração de spin inicial para toda a rede pode ser escolhida arbitrariamente. Então, uma caminhada aleatória no espaço de energia é iniciada pela formação de estados de teste, cada um dos quais é produzido escolhendo aleatoriamente um spin e alterando seu estado.
Cada vez que uma energia é visitada, o histograma é incrementado em 1. A estimativa de é então modificada por um fator multiplicativo , e o valor atualizado realiza um passeio aleatório adicional no espaço de .
Se e são as energias antes e depois de um valor de spin ser alterado, a probabilidade de transição da energia para é dada por
A razão das probabilidades de transição de para e de a podem ser calculados como
Logo, o algoritmo de passeio aleatório satisfaz o equilíbrio detalhado:
onde é a probabilidade na energia e é a probabilidade de transição de para .
Se o estado de energia é aceito, a densidade de estados é multiplicada pelo fator de modificação de maneira que e a entrada no histograma para é atualizada de forma . Se o estado de energia não é aceito, a densidade de estados é multiplicada pelo fator de modificação, e é atualizada de forma .
Flatness
O procedimento de passeio aleatório é seguido até o histograma estar reto (do inglês, "flat"), e para determinar isso, a cada iterações verificamos se todos valores possíveis de estão a uma distância, no máximo, de . A variável é denominada "flatness". Quando o histograma está reto, todos estados de energia foram visitados aproximadamente igualmente.
O número de passos, </math> n </math> que devemos realizar antes de checar deve ser maior que onde indica o tamanho da rede, para que o algoritmo tenha a oportunidade de visitar cada estado pelo menos uma vez.
Para sistemas simples, podemos utilizar um valor tão alto quanto 95%, entretanto, para este trabalho foi escolhido o valor de 80%.
Fator de modificação
Em geral, como se torna muito grande, trabalhamos com o logaritmo natural dessas quantidades, . Portanto, cada atualização da densidade de estados é dada por . O valor comumente utilizado para o fator de modificação é .
Quando o histograma é considerado reto, pelas condições descritas acima, reduzimos o valor de de forma que o novo valor será , resetamos o histograma e recomeçamos o passeio aleatório.
A simulação é parada para um valor de predeterminado. No caso, usamos .
Aplicação ao Modelo de Ising 2D
Modelo de Ising
O modelo de Ising é uma rede 2D, de tamanho que consiste de uma variável discreta em cada sítio que pode ser usada para representar o momento de dipolo magnético de um átomo[3] Cada sítio pode ter o valor de spin ou .
O hamiltoniano de interação pode ser calculado por onde indica pares distintos de vizinhos-mais-próximos.
Algoritmo
Resumindo, o passo a passo do algoritmo pode ser escrito como:
1. Defino para todos e o fator de modificação inicial ;
2. Aleatoriamente, escolho um spin e troco o seu valor. Aceito a transição com probabilidade ;
3. Modifico a densidade de estados e atualizo o histograma ;
4. Continuo até o histograma estar reto, então diminuo o valor de pela metade e reseto o histograma ;
5. Repito os passos 2-4 até .
Implementação
Resultados
Referências
<references>
- ↑ D. P. Landau, Shan-ho Tsai, M. Exler, A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling, American Journal of Physics 72, 1294 (2004). https://doi.org/10.1119/1.1707017
- ↑ P. D. Beale, Exact Distribution of Energies in the Two-Dimensional Ising Model, Phys. Rev. Lett. 76,78 (1996). https://doi.org/10.1103/PhysRevLett.76.78
- ↑ A. Rosa, C. Pires, L. Doria, Ising 2D, Wikia da Física Computacional da UFRGS. https://fiscomp.if.ufrgs.br/index.php/Ising_2D#Modelo_de_Ising