Modelo espacialmente explícito: mudanças entre as edições
(Criou página com '{{Ecologia| Modelo de Lotka-Volterra amortecido | - }} {{Ecologia| Modelo de Lotka-Volterra amortecido | - }}') |
Sem resumo de edição |
||
| (9 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Modelo de | {{Ecologia| [[Modelo de Levins aprimorado para 3 espécies]] | - }} | ||
=== Características === | |||
{{Ecologia| [[Modelo de | O modelo foi construído para ser coerente com o [[contexto]] ecológico da região norte da patagônia. | ||
*<math display="inline">L\times L</math> fragmentos que pode estar destruídos, vagos ou ocupados (por uma ou mais espécies): | |||
*<math display="inline">x_{i}\rightarrow</math> denota a fração de fragmentos ocupados por herbívoros da espécie <math display="inline">i</math> (<math display="inline">1:</math> guanaco, <math display="inline">2:</math> ovelha); | |||
*<math display="inline">y\rightarrow</math> fração ocupada por predadores; | |||
*Tempo avança discretamente e os seguintes passos ocorrem de forma síncrona: | |||
**'''Colonização''': um fragmento disponível pode ser colonizado pela espécie <math display="inline">\alpha\in\left\{ x_{1},x_{2},y\right\}</math> por um fragmento como primeiro vizinho ocupado, com probabilidade de colonização <math display="inline">c_{\alpha}</math> | |||
**'''Extinção''': Um fragmento ocupado pode se tornar vago pela espécie <math display="inline">\alpha</math> por probabilidade de extinção local <math display="inline">e_{\alpha}</math> | |||
***'''Predação''': Um fragmento que é ocupado tanto por presa quanto um predador, tem uma probabilidade de extinção da presa, dada por uma probabilidade <math display="inline">\mu_{\alpha}</math> (<math display="inline">\mu_{y}=0</math>). Neste caso então é utilizado a probabilidade de extinção local (<math>e_\alpha+\mu_\alpha </math>), ou seja, consideramos como eventos mutuamente exclusivos. | |||
**'''Deslocamento competitivo''': Um fragmento ocupado por ambos herbívoros, pode ser liberado do herbívoro inferior (<math display="inline">x_{2}</math>) com probabilidade <math display="inline">c_{x_{1}}</math>. | |||
Se temos <math display="inline">n</math> vizinhos ocupados na vizinhança de um fragmento disponível para a colonização, a probabilidade de ser colonizado por qualquer um dos vizinhos é dado por: | |||
<math display="block">p_{\alpha}=1-\left(1-c_{\alpha}\right)^{n}</math>Uma vez que <math display="inline">b_{\alpha}=\left(1-c_{\alpha}\right)</math> é a probabilidade de que <math display="inline">\alpha</math> não colonize o fragmento. Como são eventos independentes a probabilidade de não colonizar tendo 4 vizinhos ocupados por exemplo, seria: <math display="inline">b_{\alpha}b_{\alpha}b_{\alpha}b_{\alpha}=b_{\alpha}^{4}</math>, logo a probabilidade de colonizar é dada por <math display="inline">p_{\alpha}=1-b_{\alpha}^{4}</math>. A dinâmica do modelo é estudada através de uma simulação computacional realizada em um sistema fechado por barreiras impenetráveis, isto é, o perímetro é composto por fragmentos destruídos, então a grade tem tamanho <math display="inline">L+2\times L+2</math>. O algoritmo pode ser sintetizado nos seguintes passos: | |||
#Definir os parâmetros do modelo; | |||
#Destruir a fração <math display="inline">D</math> de fragmentos; | |||
#Distribuir a população inicial: | |||
#*Cada herbívoro ocupa 50% dos fragmentos disponíveis. | |||
#*O predador ocupa 50% dos fragmentos ocupados por herbívoros. | |||
#O sistema evolui de forma síncrona seguindo regras estocástica e os eventos discutidos anteriormente; | |||
#O sistema evolui durante um transiente (por volta de 3000 passos) até que a flutuação nas populações se estabilize; | |||
#Média temporal: é realizada então a média temporal (tipicamente ao longo dos últimos 2000 passos da atual simulação) da fração de fragmentos ocupados por cada espécie na atua simulação. | |||
#Média do ensemble: São realizadas nova simulações (tipicamente 100) com os mesmos parâmetros, e então é calculado médias do conjunto das frações ocupadas por cada espécie. | |||
Um ensemble nada mais é que uma idealização consistindo de um largo número de cópias mentais de um sistema, onde cada uma destas cópias corresponde a um possível estado que o sistema pode estar. Basicamente uma coleção onde todas cópias possuem as mesmas propriedades, porém em estados diferentes<ref>[https://ocw.mit.edu/courses/physics/8-08-statistical-physics-ii-spring-2005/lecture-notes/microcanonical_en.pdf Statistical Ensembles] (Instituto de Tecnologia de Massachusetts)</ref>. Dessa forma, enquanto uma média temporal (ou espacial) é a quantidade média de uma certa quantidade de um único sistema em um certo intervalo de tempo (ou espaço), a média do ensemble é quantidade média de uma certa quantidade entre muitos sistemas idênticas em um certo momento no tempo (ou espaço)<ref>[https://www.nii.ac.jp/qis/first-quantum/e/forStudents/lecture/pdf/noise/chapter1.pdf Mathematical Methods] (Yoshihisa Yamamoto, Instituto Nacional de Informática)</ref>. | |||
====Controle de predação==== | |||
Foi analisado o sistema em diferentes cenários buscando entender a dependência do estado do sistema para diferentes probabilidades de extinção de predadores e destruição do habitat. Estes parâmetros foram escolhidos pois tem origem antropogênicas. A primeira análise analisamos a a controle de predação, varia-se a probabilidade de extinção do predador (<math display="inline">e_{y}</math>) para obter a fração ocupada pelas três espécies após o sistema estar em equilíbrio. Os parâmetros são: | |||
*<math display="inline">D=0.3</math> | |||
*<math display="inline">c_{x_{2}}=0.1>c_{x_{1}}=0.05</math> | |||
*<math display="inline">e_{x_{2}}=0.01<e_{x_{1}}=0.05</math> | |||
*<math display="inline">\mu_{x_{2}}=0.8\gg\mu_{x_{1}}=0.2</math> | |||
*<math display="inline">c_{y}=0.015</math> | |||
*<math display="inline">L=100</math> | |||
Além disso, para cada valor de <math display="inline">e_{y}</math> a simulação tem a duração de 5000 passos e é calculada então a média temporal de simulação para os últimos 2000 passos. É executado 100 simulações para cada valor de <math>e_y</math> e então é obtido a média do ensemble. | |||
===Destruição do habitat=== | |||
A segunda análise é inspirada nos três cenários discutido no [[contexto]]. cada cenário é identificado por um fração diferente de destruição do habitat: | |||
*Baixo conflito: <math display="inline">D=0.1</math> | |||
*Médio conflito: <math display="inline">D=0.3</math> | |||
*Alto conflito: <math display="inline">D=0.5</math> | |||
Para baixo e alto conflito é executado uma simulação de 9000 passos enquanto para médio conflito é executado de 18000 passos. Porém todas compartilham do fator em comum que as ovelhas são retiradas no passo <math display="inline">5000</math> e então é realizado a seguinte alteração de parâmetros para reiniciar a simulação: | |||
*<math display="inline">c_{x_{1}}=0.05\rightarrow0.1</math> | |||
*<math display="inline">e_{x_{1}}=0.05\rightarrow0.025</math> | |||
*<math display="inline">e_{y}=0.02\rightarrow0.015</math> | |||
*<math display="inline">\mu_{x_{1}}=0.2\rightarrow0.3</math> | |||
Vale destacar que aqui as simulações são executadas para um valor fixo de <math display="inline">e_{y}</math>, e que com o reinicio da simulação, as espécies apesar de manterem a mesma fração ocupada, acabam sendo redistribuídas aleatoriamente pelo habitat. | |||
===Resultados=== | |||
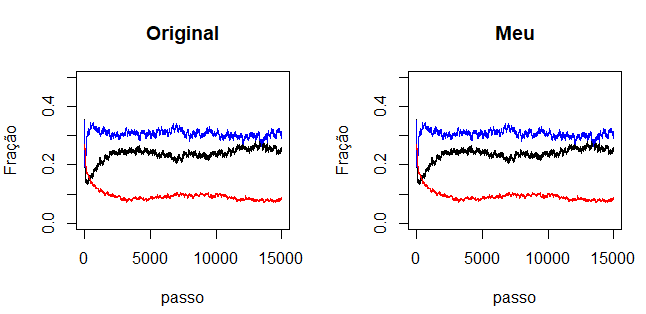
Primeiro vamos comparando resultado da simulação do código disponível abaixo com os dados originais: | |||
<div class="center">[[Ficheiro:comparacao.png|centro|miniaturadaimagem|Comparação entre os dados originais e os gerados pelo código em Python para uma evolução temporal com <math>e_y=0.017</math>.|alt=|646x314px]] | |||
</div> | |||
O módulo da diferença entre a fração final ocupada por cada espécie do código em Python e os dados originais foram: | |||
*<math display="inline">\left|\Delta x_{1}\right|=3.22\times10^{-8}</math> | |||
*<math display="inline">\left|\Delta x_{2}\right|=9.12\times10^{-9}</math> | |||
*<math display="inline">\left|\Delta y\right|=1.15\times10^{-9}</math> | |||
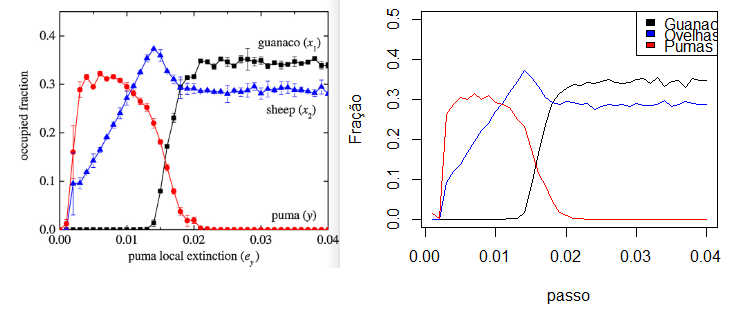
Variando então a taxa de extinção local dos pumas (<math display="inline">e_{y}</math>) para e calculando as médias dos ensembles temos: | |||
[[Ficheiro:media_esemble.png|centro|miniaturadaimagem|729x318px|A esquerda o gráfico retirado do artigo, e a direita o gerado em Python. ]] | |||
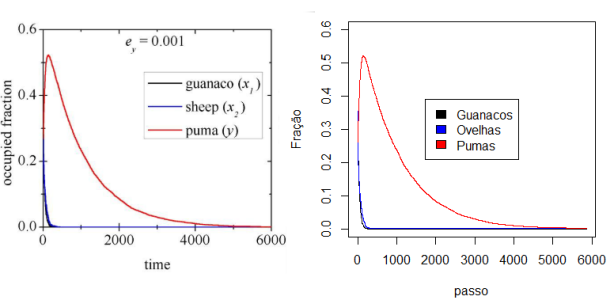
Porém devido à limitação de recursos computacionais, foi executado apenas 1 vez a simulação com cada valor <math>e_y</math>. Além disso foi reproduzido o cenário para <math display="inline">e_{y}=0.001</math>. | |||
[[Ficheiro:0001.png|centro|miniaturadaimagem|614x300px|A esquerda o gráfico retirado do artigo, e a direita o gerado em Python. ]] | |||
Conforme discutido, também foi simulado o cenário de conflitos:<div class="center">[[Ficheiro:conflitos.png|centro|miniaturadaimagem|397x300px|as três imagens superiores se referem aos gráficos gerados via Python e as inferiores ás originais do artigo.]] | |||
</div> | |||
<div align="center"> | |||
{| class="wikitable" | |||
| align="center" |Espécie | |||
| align="center" |Baixo conflito | |||
| align="center" | | |||
| align="center" |Médio Conflito | |||
| align="center" | | |||
| align="center" | Alto Conflito | |||
| align="center" | | |||
|- | |||
| align="center" | | |||
| align="center" |Artigo | |||
| align="center" |Meu | |||
| align="center" |Artigo | |||
| align="center" | Meu | |||
| align="center" | Artigo | |||
| align="center" |Meu | |||
|- | |||
| align="center" |Guanaco (<math display="inline">x_{1}</math>) | |||
| align="center" |<math display="inline">0.35\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.34\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.32\rightarrow0.45</math> | |||
| align="center" |<math display="inline">0.31\rightarrow0.44</math> | |||
| align="center" |<math display="inline">0.03\rightarrow0.20</math> | |||
| align="center" |<math display="inline">0.02\rightarrow0.18</math> | |||
|- | |||
| align="center" | Ovelha (<math display="inline">x_{2}</math>) | |||
| align="center" |<math display="inline">0.26\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.24\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.29\rightarrow0.00</math> | |||
| align="center" |<math display="inline">0.27\rightarrow0.00</math> | |||
|- | |||
| align="center" |Puma (<math display="inline">y</math>) | |||
| align="center" |<math display="inline">0.25\rightarrow0.48</math> | |||
| align="center" |<math display="inline">0.25\rightarrow0.47</math> | |||
| align="center" |<math display="inline">0.02\rightarrow0.17</math> | |||
| align="center" |<math display="inline">0.01\rightarrow0.19</math> | |||
| align="center" |<math display="inline">0.00\rightarrow<0.01</math> | |||
| align="center" |<math display="inline">0.00\rightarrow0.00</math> | |||
|} | |||
</div> | |||
=== Códigos=== | |||
O seguinte código em fortran foi utilizado para gerar os números pseudo-aleatórios:<pre> | |||
! Gerador de números pseudo-aleatórios | |||
! Jhordan Silveira de Borba | |||
! sbjhordan@gmail.com | |||
program mytest1 | |||
real RAN2 | |||
EXTERNAL RAN2 | |||
IDUM= -135 | |||
open (unit=1,file="psd.dat") | |||
DO i=1,2000000000 | |||
write(1,*),real(RAN2(IDUM)) | |||
!print *,i | |||
END DO | |||
close(1) | |||
end | |||
FUNCTION RAN2(IDUM) | |||
PARAMETER (M=714025,IA=1366,IC=150889,RM=1.4005112E-6) | |||
DIMENSION IR(97) | |||
save IR, IY | |||
DATA IFF /0/ | |||
IF(IDUM.LT.0.OR.IFF.EQ.0)THEN | |||
IFF=1 | |||
IDUM=MOD(IC-IDUM,M) | |||
DO J=1,97 | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IR(J)=IDUM | |||
END DO | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IY=IDUM | |||
ENDIF | |||
J=1+(97*IY)/M | |||
IF(J.GT.97.OR.J.LT.1)PAUSE | |||
IY=IR(J) | |||
RAN2=IY*RM | |||
IDUM=MOD(IA*IDUM+IC,M) | |||
IR(J)=IDUM | |||
RETURN | |||
END | |||
</pre>E o seguinte código base em Python é responsável pela simulação: | |||
# -*- coding: UTF-8 -*- | |||
# Modelo espacialmente explícito | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
#Bibliotecas | |||
import numpy as np # Biblioteca de funções matemáticas | |||
import copy # Biblioteca com funções para copiar | |||
#CONDIÇÕES INICIAIS ------------------------------------------------------ | |||
maxt = 15000 #tiempo total de cada realizacion | |||
Lx = 100 #tamaño del sustrato | |||
Ly = 100 | |||
#Fracciones iniciales | |||
D = 0.3 #fraccion inicial de sitios destruidos | |||
x10 = 0.5 #fraccion inicial de sitios ocupados por x1 | |||
x20 = 0.5 #fraccion inicial de sitios ocupados por x2 | |||
y0 = 0.5 #fraccion inicial de sitios ocupados por y | |||
#Tasas | |||
cx1 = 0.05 #colonizaciones | |||
cx2 = 0.1 | |||
cy = 0.015 | |||
ex1 = 0.05 #extinciones | |||
ex2 = 0.01 | |||
ey = 0.017 | |||
mx1y = 0.2 #depredaciones | |||
mx2y = 0.8 | |||
depx1 = ex1+mx1y #mortalidad aumentada=extincion+depredacion | |||
depx2 = ex2+mx2y | |||
g = open("psd.dat", "r") | |||
#Inicializaciones | |||
s = np.full((Lx, Ly), [1]) #matriz de habitat (1=sitio disponible, 0=destruido) | |||
x1 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
x2 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
y = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio | |||
for i in range(1,Lx-1): | |||
for j in range (1,Ly-1): | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < D): s[i,j]=0 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < x10 and s[i,j]==1): x1[i,j]=1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < x20 and s[i,j]==1): x2[i,j]=1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if ((x1[i,j]==1 or x2[i,j]==1) and rnd < y0): y[i,j]=1 | |||
for i in range(Lx): #destruimos los bordes del habitat | |||
s[i,0]=0 | |||
s[i,Ly-1]=0 | |||
for j in range(Ly): | |||
s[0,j]=0 | |||
s[Lx-1,j]=0 | |||
#------------------------------------------------------- | |||
#Lazo temporal | |||
fx1=sum(sum(x1))/((Lx-2)*(Ly-2)) | |||
fx2=sum(sum(x2))/((Lx-2)*(Ly-2)) | |||
fy =sum(sum(y)) /((Lx-2)*(Ly-2)) | |||
f = open("minha.dat", "w") | |||
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n") | |||
for it in range(maxt): | |||
if (float(it)%(float(maxt)/100)==0.): | |||
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual | |||
x1old=copy.copy(x1) #poblaciones del paso anterior | |||
x2old=copy.copy(x2) | |||
yold=copy.copy(y) | |||
#Recorro la malla | |||
for i in range (1,Lx-1): | |||
for j in range (1,Ly-1): | |||
#colonizaciones | |||
if (x1old[i,j]==0 and s[i,j]==1): #colonizacion de x1 si el sitio esta libre de x1 y no destruido: | |||
nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cx1)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p):x1[i,j]=1 | |||
if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0): #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido: | |||
nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cx2)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p): x2[i,j]=1 | |||
ocup=0 #ocupacion de herbivoros | |||
if (x1old[i,j]==1 or x2old[i,j]==1): ocup=1 | |||
if (yold[i,j]==0 and ocup==1): #colonizacion de y si el sitio está libre de y,y ocupado por un x | |||
nvec=yold[i-1,j]+yold[i+1,j]+yold[i,j-1]+yold[i,j+1] #cantidad de vecinos ocupados | |||
p=1.0-(1.0-cy)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < p): y[i,j]=1 | |||
#extinciones sin depredadores | |||
if (x1old[i,j]==1 and yold[i,j]==0): #extincion de x1 si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ex1): x1[i,j]=0 | |||
if (x2old[i,j]==1 and yold[i,j]==0): #extincion de x2 si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ex2): x2[i,j]=0 | |||
if (yold[i,j]==1): #extincion de y si el sitio esta ocupado | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < ey): y[i,j]=0 | |||
#depredacion (extinción de presas donde hay depredadores) | |||
if (x1old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x1 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < depx1): x1[i,j]=0 | |||
if (x2old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x2 | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < depx2): x2[i,j]=0 | |||
#desplazamiento por competencia (jerarquia) | |||
if (x1old[i,j]==1 and x2old[i,j]==1): | |||
rnd=float(g.readline())#np.random.rand() | |||
if (rnd < cx1): x2[i,j]=0 | |||
fx1=sum(sum(x1))/((Lx-2)*(Ly-2)) | |||
fx2=sum(sum(x2))/((Lx-2)*(Ly-2)) | |||
fy =sum(sum(y)) /((Lx-2)*(Ly-2)) | |||
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n") | |||
f.close | |||
g.close() | |||
Além disso, foi usado o script em R para gerar os gráficos comparando dois conjunto de dados, este script é facilmente editável pra exibir o resultado de apenas uma simulação:<pre> | |||
# Visualização de gráficos | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
Dados0 <- read.table("Endereço do arquivo 0") | |||
Dados1 <- read.table("Endereço do arquivo 1") | |||
par(mfrow=c(1,2)) | |||
plot( c(Dados0[,1]), c(Dados0[,2]), col="black", main="Original", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5)) | |||
lines(c(Dados0[,1]), c(Dados0[,3]), col="blue") | |||
lines(c(Dados0[,1]), c(Dados0[,4]), col="red") | |||
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red")) | |||
plot( c(Dados1[,1]), c(Dados1[,2]), col="black", main="Meu", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5)) | |||
lines(c(Dados1[,1]), c(Dados1[,3]), col="blue") | |||
lines(c(Dados1[,1]), c(Dados1[,4]), col="red") | |||
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red")) | |||
</pre> | |||
===Principal material utilizado=== | |||
#[https://arxiv.org/pdf/1409.0024.pdf Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances] (Fabiana Laguna e outros, Ecological Modelling) | |||
===Referências=== | |||
<references /> | |||
{{Ecologia| [[Modelo de Levins aprimorado para 3 espécies]] | - }} | |||
Edição atual tal como às 19h45min de 13 de abril de 2021
Anterior: Modelo de Levins aprimorado para 3 espécies | Índice: Ecologia | Próximo: -
Características
O modelo foi construído para ser coerente com o contexto ecológico da região norte da patagônia.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle L\times L} fragmentos que pode estar destruídos, vagos ou ocupados (por uma ou mais espécies):
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{i}\rightarrow} denota a fração de fragmentos ocupados por herbívoros da espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle i} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 1:} guanaco, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 2:} ovelha);
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle y\rightarrow} fração ocupada por predadores;
- Tempo avança discretamente e os seguintes passos ocorrem de forma síncrona:
- Colonização: um fragmento disponível pode ser colonizado pela espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha\in\left\{ x_{1},x_{2},y\right\}} por um fragmento como primeiro vizinho ocupado, com probabilidade de colonização Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{\alpha}}
- Extinção: Um fragmento ocupado pode se tornar vago pela espécie Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha}
por probabilidade de extinção local Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{\alpha}}
- Predação: Um fragmento que é ocupado tanto por presa quanto um predador, tem uma probabilidade de extinção da presa, dada por uma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu_{\alpha}} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu_{y}=0} ). Neste caso então é utilizado a probabilidade de extinção local (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_\alpha+\mu_\alpha } ), ou seja, consideramos como eventos mutuamente exclusivos.
- Deslocamento competitivo: Um fragmento ocupado por ambos herbívoros, pode ser liberado do herbívoro inferior (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{2}} ) com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{x_{1}}} .
Se temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle n} vizinhos ocupados na vizinhança de um fragmento disponível para a colonização, a probabilidade de ser colonizado por qualquer um dos vizinhos é dado por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\alpha}=1-\left(1-c_{\alpha}\right)^{n}} Uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle b_{\alpha}=\left(1-c_{\alpha}\right)} é a probabilidade de que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \alpha} não colonize o fragmento. Como são eventos independentes a probabilidade de não colonizar tendo 4 vizinhos ocupados por exemplo, seria: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle b_{\alpha}b_{\alpha}b_{\alpha}b_{\alpha}=b_{\alpha}^{4}} , logo a probabilidade de colonizar é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle p_{\alpha}=1-b_{\alpha}^{4}} . A dinâmica do modelo é estudada através de uma simulação computacional realizada em um sistema fechado por barreiras impenetráveis, isto é, o perímetro é composto por fragmentos destruídos, então a grade tem tamanho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle L+2\times L+2} . O algoritmo pode ser sintetizado nos seguintes passos:
- Definir os parâmetros do modelo;
- Destruir a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D} de fragmentos;
- Distribuir a população inicial:
- Cada herbívoro ocupa 50% dos fragmentos disponíveis.
- O predador ocupa 50% dos fragmentos ocupados por herbívoros.
- O sistema evolui de forma síncrona seguindo regras estocástica e os eventos discutidos anteriormente;
- O sistema evolui durante um transiente (por volta de 3000 passos) até que a flutuação nas populações se estabilize;
- Média temporal: é realizada então a média temporal (tipicamente ao longo dos últimos 2000 passos da atual simulação) da fração de fragmentos ocupados por cada espécie na atua simulação.
- Média do ensemble: São realizadas nova simulações (tipicamente 100) com os mesmos parâmetros, e então é calculado médias do conjunto das frações ocupadas por cada espécie.
Um ensemble nada mais é que uma idealização consistindo de um largo número de cópias mentais de um sistema, onde cada uma destas cópias corresponde a um possível estado que o sistema pode estar. Basicamente uma coleção onde todas cópias possuem as mesmas propriedades, porém em estados diferentes[1]. Dessa forma, enquanto uma média temporal (ou espacial) é a quantidade média de uma certa quantidade de um único sistema em um certo intervalo de tempo (ou espaço), a média do ensemble é quantidade média de uma certa quantidade entre muitos sistemas idênticas em um certo momento no tempo (ou espaço)[2].
Controle de predação
Foi analisado o sistema em diferentes cenários buscando entender a dependência do estado do sistema para diferentes probabilidades de extinção de predadores e destruição do habitat. Estes parâmetros foram escolhidos pois tem origem antropogênicas. A primeira análise analisamos a a controle de predação, varia-se a probabilidade de extinção do predador (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}} ) para obter a fração ocupada pelas três espécies após o sistema estar em equilíbrio. Os parâmetros são:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.3}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{x_{2}}=0.1>c_{x_{1}}=0.05}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{x_{2}}=0.01<e_{x_{1}}=0.05}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu_{x_{2}}=0.8\gg\mu_{x_{1}}=0.2}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{y}=0.015}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle L=100}
Além disso, para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}} a simulação tem a duração de 5000 passos e é calculada então a média temporal de simulação para os últimos 2000 passos. É executado 100 simulações para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_y} e então é obtido a média do ensemble.
Destruição do habitat
A segunda análise é inspirada nos três cenários discutido no contexto. cada cenário é identificado por um fração diferente de destruição do habitat:
- Baixo conflito: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.1}
- Médio conflito: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.3}
- Alto conflito: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle D=0.5}
Para baixo e alto conflito é executado uma simulação de 9000 passos enquanto para médio conflito é executado de 18000 passos. Porém todas compartilham do fator em comum que as ovelhas são retiradas no passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 5000} e então é realizado a seguinte alteração de parâmetros para reiniciar a simulação:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle c_{x_{1}}=0.05\rightarrow0.1}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{x_{1}}=0.05\rightarrow0.025}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}=0.02\rightarrow0.015}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \mu_{x_{1}}=0.2\rightarrow0.3}
Vale destacar que aqui as simulações são executadas para um valor fixo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}} , e que com o reinicio da simulação, as espécies apesar de manterem a mesma fração ocupada, acabam sendo redistribuídas aleatoriamente pelo habitat.
Resultados
Primeiro vamos comparando resultado da simulação do código disponível abaixo com os dados originais:
O módulo da diferença entre a fração final ocupada por cada espécie do código em Python e os dados originais foram:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|\Delta x_{1}\right|=3.22\times10^{-8}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|\Delta x_{2}\right|=9.12\times10^{-9}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle \left|\Delta y\right|=1.15\times10^{-9}}
Variando então a taxa de extinção local dos pumas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}} ) para e calculando as médias dos ensembles temos:
Porém devido à limitação de recursos computacionais, foi executado apenas 1 vez a simulação com cada valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_y} . Além disso foi reproduzido o cenário para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle e_{y}=0.001} .
Conforme discutido, também foi simulado o cenário de conflitos:
| Espécie | Baixo conflito | Médio Conflito | Alto Conflito | |||
| Artigo | Meu | Artigo | Meu | Artigo | Meu | |
| Guanaco (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{1}} ) | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.35\rightarrow0.47} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.34\rightarrow0.47} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.32\rightarrow0.45} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.31\rightarrow0.44} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.03\rightarrow0.20} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.02\rightarrow0.18} |
| Ovelha (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle x_{2}} ) | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.26\rightarrow0.00} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.24\rightarrow0.00} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.29\rightarrow0.00} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.29\rightarrow0.00} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.29\rightarrow0.00} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.27\rightarrow0.00} |
| Puma (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle y} ) | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.25\rightarrow0.48} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.25\rightarrow0.47} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.02\rightarrow0.17} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.01\rightarrow0.19} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.00\rightarrow<0.01} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\textstyle 0.00\rightarrow0.00} |
Códigos
O seguinte código em fortran foi utilizado para gerar os números pseudo-aleatórios:
! Gerador de números pseudo-aleatórios ! Jhordan Silveira de Borba ! sbjhordan@gmail.com program mytest1 real RAN2 EXTERNAL RAN2 IDUM= -135 open (unit=1,file="psd.dat") DO i=1,2000000000 write(1,*),real(RAN2(IDUM)) !print *,i END DO close(1) end FUNCTION RAN2(IDUM) PARAMETER (M=714025,IA=1366,IC=150889,RM=1.4005112E-6) DIMENSION IR(97) save IR, IY DATA IFF /0/ IF(IDUM.LT.0.OR.IFF.EQ.0)THEN IFF=1 IDUM=MOD(IC-IDUM,M) DO J=1,97 IDUM=MOD(IA*IDUM+IC,M) IR(J)=IDUM END DO IDUM=MOD(IA*IDUM+IC,M) IY=IDUM ENDIF J=1+(97*IY)/M IF(J.GT.97.OR.J.LT.1)PAUSE IY=IR(J) RAN2=IY*RM IDUM=MOD(IA*IDUM+IC,M) IR(J)=IDUM RETURN END
E o seguinte código base em Python é responsável pela simulação:
# -*- coding: UTF-8 -*-
# Modelo espacialmente explícito
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
#Bibliotecas
import numpy as np # Biblioteca de funções matemáticas
import copy # Biblioteca com funções para copiar
#CONDIÇÕES INICIAIS ------------------------------------------------------
maxt = 15000 #tiempo total de cada realizacion
Lx = 100 #tamaño del sustrato
Ly = 100
#Fracciones iniciales
D = 0.3 #fraccion inicial de sitios destruidos
x10 = 0.5 #fraccion inicial de sitios ocupados por x1
x20 = 0.5 #fraccion inicial de sitios ocupados por x2
y0 = 0.5 #fraccion inicial de sitios ocupados por y
#Tasas
cx1 = 0.05 #colonizaciones
cx2 = 0.1
cy = 0.015
ex1 = 0.05 #extinciones
ex2 = 0.01
ey = 0.017
mx1y = 0.2 #depredaciones
mx2y = 0.8
depx1 = ex1+mx1y #mortalidad aumentada=extincion+depredacion
depx2 = ex2+mx2y
g = open("psd.dat", "r")
#Inicializaciones
s = np.full((Lx, Ly), [1]) #matriz de habitat (1=sitio disponible, 0=destruido)
x1 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
x2 = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
y = np.full((Lx, Ly), [0]) #1 = sitio ocupado, 0 sitio vazio
for i in range(1,Lx-1):
for j in range (1,Ly-1):
rnd=float(g.readline())#np.random.rand()
if (rnd < D): s[i,j]=0
rnd=float(g.readline())#np.random.rand()
if (rnd < x10 and s[i,j]==1): x1[i,j]=1
rnd=float(g.readline())#np.random.rand()
if (rnd < x20 and s[i,j]==1): x2[i,j]=1
rnd=float(g.readline())#np.random.rand()
if ((x1[i,j]==1 or x2[i,j]==1) and rnd < y0): y[i,j]=1
for i in range(Lx): #destruimos los bordes del habitat
s[i,0]=0
s[i,Ly-1]=0
for j in range(Ly):
s[0,j]=0
s[Lx-1,j]=0
#-------------------------------------------------------
#Lazo temporal
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fy =sum(sum(y)) /((Lx-2)*(Ly-2))
f = open("minha.dat", "w")
f.write(" "+str(0)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
for it in range(maxt):
if (float(it)%(float(maxt)/100)==0.):
print("Porcentagem: "+str(it*100/maxt)) # Exibe o passo atual
x1old=copy.copy(x1) #poblaciones del paso anterior
x2old=copy.copy(x2)
yold=copy.copy(y)
#Recorro la malla
for i in range (1,Lx-1):
for j in range (1,Ly-1):
#colonizaciones
if (x1old[i,j]==0 and s[i,j]==1): #colonizacion de x1 si el sitio esta libre de x1 y no destruido:
nvec=x1old[i-1,j]+x1old[i+1,j]+x1old[i,j-1]++x1old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx1)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p):x1[i,j]=1
if (x2old[i,j]==0 and s[i,j]==1 and x1old[i,j]==0): #colonizacion de x2 si el sitio esta libre de x1 y x2, y no destruido:
nvec=x2old[i-1,j]+x2old[i+1,j]+x2old[i,j-1]+x2old[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cx2)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p): x2[i,j]=1
ocup=0 #ocupacion de herbivoros
if (x1old[i,j]==1 or x2old[i,j]==1): ocup=1
if (yold[i,j]==0 and ocup==1): #colonizacion de y si el sitio está libre de y,y ocupado por un x
nvec=yold[i-1,j]+yold[i+1,j]+yold[i,j-1]+yold[i,j+1] #cantidad de vecinos ocupados
p=1.0-(1.0-cy)**nvec #probabilidad de ser colonizado= 1 - prob de quedar libre
rnd=float(g.readline())#np.random.rand()
if (rnd < p): y[i,j]=1
#extinciones sin depredadores
if (x1old[i,j]==1 and yold[i,j]==0): #extincion de x1 si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ex1): x1[i,j]=0
if (x2old[i,j]==1 and yold[i,j]==0): #extincion de x2 si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ex2): x2[i,j]=0
if (yold[i,j]==1): #extincion de y si el sitio esta ocupado
rnd=float(g.readline())#np.random.rand()
if (rnd < ey): y[i,j]=0
#depredacion (extinción de presas donde hay depredadores)
if (x1old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x1
rnd=float(g.readline())#np.random.rand()
if (rnd < depx1): x1[i,j]=0
if (x2old[i,j]==1 and yold[i,j]==1): #depredacion de y sobre x2
rnd=float(g.readline())#np.random.rand()
if (rnd < depx2): x2[i,j]=0
#desplazamiento por competencia (jerarquia)
if (x1old[i,j]==1 and x2old[i,j]==1):
rnd=float(g.readline())#np.random.rand()
if (rnd < cx1): x2[i,j]=0
fx1=sum(sum(x1))/((Lx-2)*(Ly-2))
fx2=sum(sum(x2))/((Lx-2)*(Ly-2))
fy =sum(sum(y)) /((Lx-2)*(Ly-2))
f.write(" "+str(it+1)+" "+str(fx1)+" "+str(fx2)+" "+str(fy)+"\n")
f.close
g.close()
Além disso, foi usado o script em R para gerar os gráficos comparando dois conjunto de dados, este script é facilmente editável pra exibir o resultado de apenas uma simulação:
# Visualização de gráficos
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
Dados0 <- read.table("Endereço do arquivo 0")
Dados1 <- read.table("Endereço do arquivo 1")
par(mfrow=c(1,2))
plot( c(Dados0[,1]), c(Dados0[,2]), col="black", main="Original", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5))
lines(c(Dados0[,1]), c(Dados0[,3]), col="blue")
lines(c(Dados0[,1]), c(Dados0[,4]), col="red")
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red"))
plot( c(Dados1[,1]), c(Dados1[,2]), col="black", main="Meu", ylab="Fração", xlab="passo" ,type="l",ylim=c(0,0.5))
lines(c(Dados1[,1]), c(Dados1[,3]), col="blue")
lines(c(Dados1[,1]), c(Dados1[,4]), col="red")
legend("topright", c("Guanacos","Ovelhas","Pumas"), fill=c("black","blue","red"))
Principal material utilizado
- Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Referências
- ↑ Statistical Ensembles (Instituto de Tecnologia de Massachusetts)
- ↑ Mathematical Methods (Yoshihisa Yamamoto, Instituto Nacional de Informática)
Anterior: Modelo de Levins aprimorado para 3 espécies | Índice: Ecologia | Próximo: -