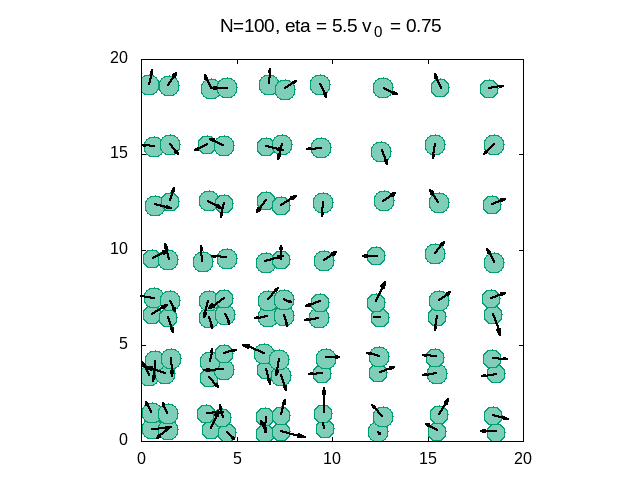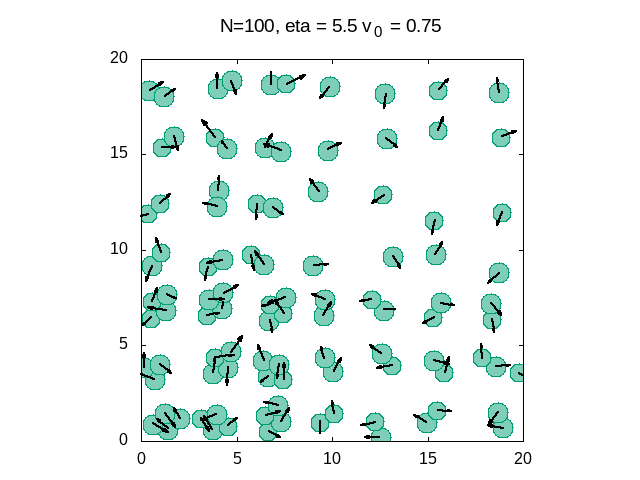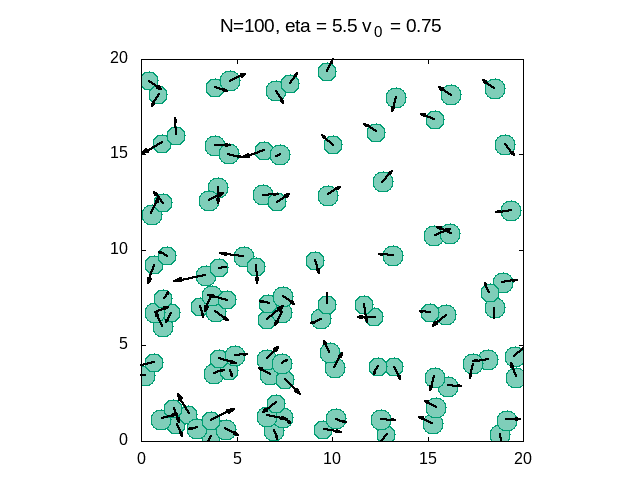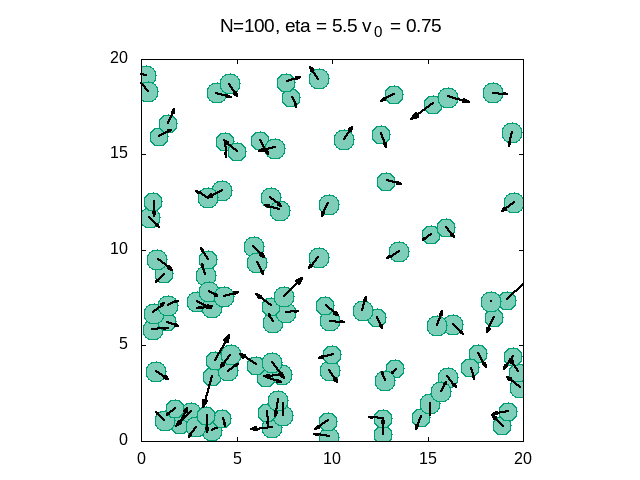Grupo - Modelo de Szabó: mudanças entre as edições
(Criou página com ''''Integrante do grupo:''' Edson Mateus Signor (282004) ==Introdução== Vemos corriqueiramente exemplos de movimentos coletivo na natureza como: cardume de peixes, bando de...') |
Sem resumo de edição |
||
| (7 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Integrante do grupo:''' Edson Mateus Signor (282004) | |||
'''Integrante do grupo:''' Edson Mateus Signor (282004) | |||
==Introdução== | ==Introdução== | ||
Vemos corriqueiramente exemplos de movimentos coletivos na natureza como: cardume de peixes, bando de pássaros, células, etc. SZABÓ et al (2006) | |||
<ref name=szabo> B.Szabó, G. J.Szöllösi, B.Gönci, Zs.Jurányi, D.Selmeczi, and T.Vicsek. PHYSICAL REVIEW E 74, 061908 (2006)</ref>criam um modelo com a finalidade de reproduzir tais comportamentos para queratócitos (células teciduais de cicatrização de feridas nas escamas de peixes). O diferencial deste modelo perante os outros é o fato de usar partículas autopropulsadas com uma interação intercelular de curto alcance muito simples. O objetivo é a partir deste modelo visualizar uma transição de fase cinética no movimento dos queratócitos, para isso definimos o chamado parâmetro de ordem, o qual mede quão ordenado está o sistema, e variamos o valor de ruído presente na representação da locomoção natural das células. | |||
==Experimento== | |||
==Experimento== | |||
Em SZABÓ et al (2006) <ref name=szabo/> realizou-se um experimento com uma grande quantidade de células de tecido (queratócitos) a fim de visualizar a migração coletiva. À medida que as células migratórias aumentam, notou-se uma transição de fase cinética de um estado desordenado para um estado ordenado. | |||
[[Arquivo:Experiment.gif|frame|200x200px|center|Gráfico 1: Migração coletiva de queratócitos para diferentes densidades. <ref>http://angel.elte.hu/~bszabo/collectivecells/</ref>]] | |||
Observa-se no vídeo do grupo que para densidades pequenas as células apresentam um movimento aparentemente aleatório, já para uma densidade intermediária há a formação de pequenos clusters, porém não seguem um sentido de movimento em comum. Entretanto para uma alta densidade o movimento torna-se coletivo todos os queratócitos seguindo na mesma direção. Além disso, realizaram medidas experimentais do parâmetro de ordem médio do sistema para vários diferentes valores de densidades de células, a partir disso chegaram ao seguinte resultado: | |||
[[Arquivo:Parametro_ordem.png|frame|300x300px|center|Gráfico 2: Gráfico do parâmetro de ordem médio variando a densidade de células de queratócitos.<ref name=szabo/>]] | |||
Assim há mais uma evidência para a transição de fase cinética de um estado desordenado para um estado ordenado. Diante disso o modelo a partir de forças atrativas-repulsivas de curto alcance é suficiente para organizar um montante de células em um movimento coerente. | |||
==O Modelo== | |||
O modelo de Szabó foi construído a fim de interpretar os resultados experimentais e seu comportamento. O modelo para as queratócitos individualmente é baseado em células autopropulsadas, onde suas velocidades são constantes numa direção bem definida. Para o ruído da locomoção das células considera-se um ruído branco na direção da autopropulsão. Além disso, considera-se para a interação intercelular forças de curto alcance, onde o movimento coletivo dos queratócitos emerge partir delas. | |||
Considerando o sistema bi-dimensional descrevemos o movimento das N células com um movimento amortecido, logo: | |||
<math>\frac{d\textbf{r}_{i}(t)}{dt}= v_{0}\textbf{n}_{i}(t) + \mu \sum_{j=1}^N \textbf{F}(\textbf{r}_{i}, \textbf{r}_{j} )</math> | |||
Cada célula com mobilidade <math>\mu </math> segue na direção da autopropulsão <math> \textbf{n}_{i}(t) </math> caso não sofra a ação das forças intercelulares. | |||
===Cálculo da autopropulsão === | |||
A direção de <math> \textbf{n}_{i}(t) </math> é dado pelo ângulo <math>\theta _{i}^{n}(t) </math>, mostrado na figura abaixo. | |||
[[Arquivo:Imagem_int_celulas.png|frame|400x400px|center|Gráfico 3: Esquematização das células de queratócitos para o modelo de Szabó.<ref name=szabo/>]] | |||
Assim, como a velocidade <math> \textbf{v}_{i}(t) </math> das células tentam ajustar sua direção (dado pelo ângulo <math>\phi _{i}^{n}(t) </math >) com a de <math> \textbf{n}_{i}(t) </math>. Então atribuímos a ela uma força restauradora, caracterizada pela equação diferencial: | |||
<math>\frac{d\theta_{i}^{n}(t)}{dt} = \frac{(\theta_{i}^{n}(t) - \phi_{i}^{n}(t))}{\tau} + \xi</math> | |||
<math>\tau</math> é o tempo de relaxação e <math>\xi</math> é o ruído branco gaussiano da autopropulsão. Usando a fórmula do produto vetorial entre <math> \textbf{v}_{i}(t) </math> e <math> \textbf{n}_{i}(t) </math> : | |||
<math>\sin\left({\theta_{i}^{n}(t) - \phi_{i}^{n}(t)}\right) = \textbf{n}_{i}(t)\frac{\textbf{v}_{i}(t_{k})}{|\textbf{v}_{i}(t_{k})|}</math> | |||
Chegamos, assim, na seguinte expressão para o ângulo <math>\theta _{i}^{n}(t) </math>: | |||
<math>\frac{d\theta_{i}^{n}(t)}{dt} = \frac{1}{\tau} arcsin\left[\left(\textbf{n}_{i}(t)\frac{\textbf{v}_{i}(t_{k})}{|\textbf{v}_{i}(t_{k})|}\right)\cdot\textbf{e}_{z}\right] + \xi</math> | |||
Onde <math> \textbf{e}_{z} </math> é o vetor unitário perpendicular ao plano de movimento dos queratócitos. Deste modo, para atualizarmos o valor de <math>n_{i}(t)</math> basta utilizarmos a seguinte expressão: | |||
<math>\textbf{n}_{i}(t) = \cos{\theta_{i}^{n}(t)} \hat{\textbf{x}} + \sin{\theta_{i}^{n}(t)}\hat{\textbf{y}}</math> | |||
===Cálculo das forças intercelulares=== | |||
As forças entre os queratócitos são funções que dependem apenas das distâncias <math> d_{ij}</math> entre os centros de massa de cada um. Os dois principais critérios para a elaboração das forças foram: (i) As células devem ter um volume bem definido e apenas interagirem com os vizinhos mais próximos e (ii) para um certo valor de <math> d_{ij}</math> as células não devem mais interagirem. Assim considerou-se os queratócitos com um volume de raio <math>R_0/2</math>, onde sofrem uma força repulsiva até uma distância <math>R_{eq}</math>, uma força atrativa entre as distâncias <math>R_{eq}</math> e <math>R_0</math> e zero para maiores que <math>R_0</math>. Então temos a seguinte forma: | |||
<math> | |||
\textbf{F}(\textbf{r}_{i}, \textbf{r}_{j} ) = \textbf{e}_{ij}\begin{cases} | |||
F_{rep}\frac{d_{ij} - R_{eq}}{R_{eq}},\quad d_{ij} < R_{eq} \\ | |||
F_{adh}\frac{d_{ij} - R_{eq}}{R_{0} - Re_{eq}}, \; \; R_{eq} \le d_{ij} \le R_{0}\\ | |||
0, \quad \quad \quad \quad \quad \; d_{ij} > R_{0}\\ | |||
\end{cases} | |||
</math> | |||
Onde <math>\textbf{e}_{ij} = \frac{\textbf{r}_{i} - \textbf{r}_{j}}{|\textbf{r}_{i} - \textbf{r}_{j} |}</math>, <math>d_{ij} = |\textbf{r}_{i} - \textbf{r}_{j} | </math>, <math>F_{rep}</math> é o máximo valor da força repulsiva para <math>d_{ij} = 0</math> e <math>F_{adh}</math> é o máximo valor da força atrativa para <math>d_{ij} = R_{0}</math> (Como pode ser visto na figura 4). | |||
[[Arquivo:Graf_forças.png|frame|400x400px|center|Gráfico 4: Gráfico das forças intercelulares.<ref name=szabo/>]] | |||
Com isso a dinâmica dos queratócitos está completa. | |||
==Resultados== | |||
Finalizado a dinâmica das células utilizou-se um programa em Python para simular os queratócitos para três diferentes valores de ruído. Porque além de apresentar uma transição de fase cinética variando a densidade (Como mostrado no experimento), também há uma transição variando a intensidade do ruído, ou seja, a potência natural da autopropulsão. Com isso, dado o programa <math>\it{Simulacao \; dos \; queratocitos\;}</math> obteve-se as seguintes simulações: | |||
[[Arquivo: Ezgif.com-gif-maker(1).gif|frame|400x400px|center|Gráfico 5: Simulação dos queratocitos para um ruído baixo.]] | |||
[[Arquivo:Ezgif.gif|frame|400x400px|center|Gráfico 6: Simulação dos queratocitos para um ruído intermediário]] | |||
[[Arquivo: Eta 5 5das.gif|frame|400x400px|center|Gráfico 7: Simulação dos queratocitos para um ruído alto]] | |||
== Parâmetro de Ordem== | |||
Para visualizar a transição de fase cinética definiu-se um parâmetro de ordem <math>V</math> onde é definido da seguinte maneira: | |||
<math>\frac{d\textbf{r}_{i}(t)}{dt}= v_{0}\textbf{n}_{i}(t) + \mu \sum_{j=1}^N \textbf{F}(\textbf{r}_{i}, \textbf{r}_{j} )</math> | |||
<math> \overline{V} = \langle V\rangle_{t_k}</math> | |||
Neste parâmetro queremos basicamente medir o quão desordenado está o sistema. Então a ideia é somar vetorialmente as velocidades de cada célula - dividida pelos seus respectivos módulos, pois só nos interessa a direção - e normalizamos pela quantidade de células. Além disso, ainda se faz uma média temporal a fim de melhorar ainda mais a medida. Tal tipo de parâmetro foi definido porque, por exemplo, se o sistema está em um estado dito desordenado esperamos os queratócitos vagando em direção aparentemente aleatórias, logo se somarmos as velocidades a resultante será um vetor nulo, e o valor de <math>\overline{V}</math> tenderá a zero. Já quando o sistema estiver um estado dito ordenado, as células estarão em um movimento coletivo, ou seja, o módulo da velocidade resultante será diferente de zero, por conseguinte, o valor de <math>\overline{V}</math> tenderá a 1. | |||
=== Resultado do Parâmetro de ordem === | |||
Antes de calcular o parâmetro <math>\overline{V}</math> fazendo a média temporal, temos que observar o gráfico da evolução temporal de <math>\overline{V}</math> (fazendo uso do programa em Python <math>\it{Evolucao \;temporal\; do \;parâmetro \;de \;ordem\;}</math>): | |||
[[Arquivo: VxT.png |frame|300x300px|center|Gráfico 8: Gráfico do parâmetro de ordem médio variando a densidade de células de queratócitos.]] | |||
Nota-se que há um transiente, com isso então para realizar o cálculo da média apenas utiliza-se os valores de <math>\overline{V}</math> para a cima de 50 interações a fim de desprezar o transiente e obter uma melhor média. | |||
Feito isto, com um outro programa em Python <math>\it{Transicao \; de \;fase \;}</math> temos o resultado obtido a partir das simulações: | |||
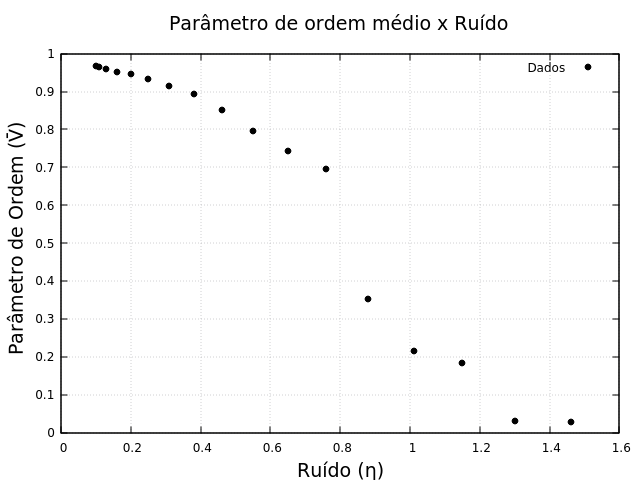
[[Arquivo: Vxeta.png |frame|300x300px|center|Gráfico 9: Gráfico do parâmetro de ordem médio em função do ruído.]] | |||
Assim, nota-se que se obteve um gráfico característico de uma transição de fase confirmando o que havíamos esperado. Fazendo uso de mais partículas pode-se chegar em um gráfico como o feito em SZABÓ et al (2006) <ref name=szabo/>. | |||
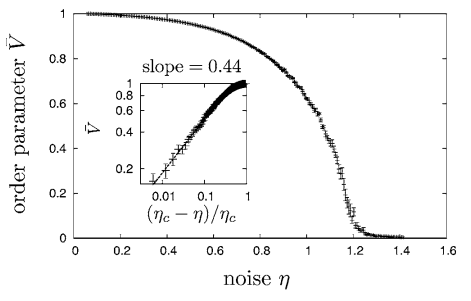
[[Arquivo: Article Vxeta.png |frame|300x300px|center|Gráfico 10: Gráfico do parâmetro de ordem médio em função do ruído obtido por Szabó <ref name=szabo/>.]] | |||
==Códigos== | |||
[https://github.com/edsonsignor/metcompC/blob/master/simula%C3%A7%C3%A3o_queratocitos.py Modelo de Szabó - Simulação dos queratócitos] | |||
[https://github.com/edsonsignor/metcompC/blob/master/verf_transiente_V.py Modelo de Szabó - Evolução temporal do parâmetro de ordem] | |||
[https://github.com/edsonsignor/metcompC/blob/master/Parametro_de_ordem.py Modelo de Szabó - Transição de fase] | |||
==Bibliografia== | |||
<references/> | |||
Edição atual tal como às 13h06min de 10 de janeiro de 2020
Integrante do grupo: Edson Mateus Signor (282004)
Introdução
Vemos corriqueiramente exemplos de movimentos coletivos na natureza como: cardume de peixes, bando de pássaros, células, etc. SZABÓ et al (2006) [1]criam um modelo com a finalidade de reproduzir tais comportamentos para queratócitos (células teciduais de cicatrização de feridas nas escamas de peixes). O diferencial deste modelo perante os outros é o fato de usar partículas autopropulsadas com uma interação intercelular de curto alcance muito simples. O objetivo é a partir deste modelo visualizar uma transição de fase cinética no movimento dos queratócitos, para isso definimos o chamado parâmetro de ordem, o qual mede quão ordenado está o sistema, e variamos o valor de ruído presente na representação da locomoção natural das células.
Experimento
Em SZABÓ et al (2006) [1] realizou-se um experimento com uma grande quantidade de células de tecido (queratócitos) a fim de visualizar a migração coletiva. À medida que as células migratórias aumentam, notou-se uma transição de fase cinética de um estado desordenado para um estado ordenado.
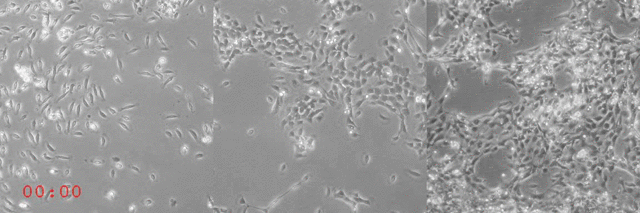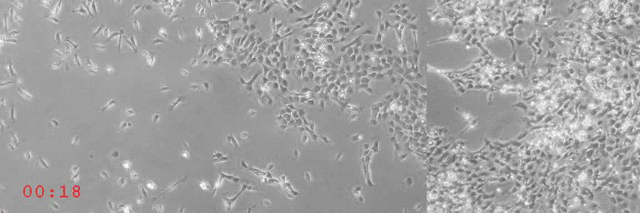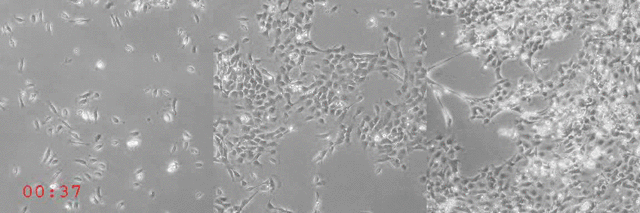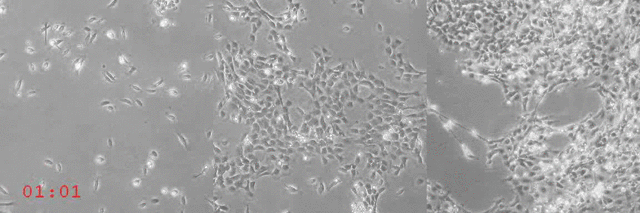
Observa-se no vídeo do grupo que para densidades pequenas as células apresentam um movimento aparentemente aleatório, já para uma densidade intermediária há a formação de pequenos clusters, porém não seguem um sentido de movimento em comum. Entretanto para uma alta densidade o movimento torna-se coletivo todos os queratócitos seguindo na mesma direção. Além disso, realizaram medidas experimentais do parâmetro de ordem médio do sistema para vários diferentes valores de densidades de células, a partir disso chegaram ao seguinte resultado:
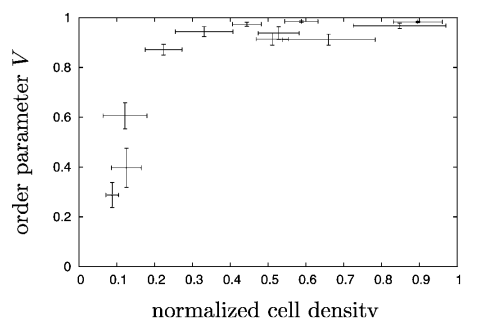
Assim há mais uma evidência para a transição de fase cinética de um estado desordenado para um estado ordenado. Diante disso o modelo a partir de forças atrativas-repulsivas de curto alcance é suficiente para organizar um montante de células em um movimento coerente.
O Modelo
O modelo de Szabó foi construído a fim de interpretar os resultados experimentais e seu comportamento. O modelo para as queratócitos individualmente é baseado em células autopropulsadas, onde suas velocidades são constantes numa direção bem definida. Para o ruído da locomoção das células considera-se um ruído branco na direção da autopropulsão. Além disso, considera-se para a interação intercelular forças de curto alcance, onde o movimento coletivo dos queratócitos emerge partir delas. Considerando o sistema bi-dimensional descrevemos o movimento das N células com um movimento amortecido, logo:
Cada célula com mobilidade segue na direção da autopropulsão caso não sofra a ação das forças intercelulares.
Cálculo da autopropulsão
A direção de é dado pelo ângulo , mostrado na figura abaixo.
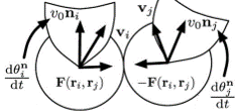
Assim, como a velocidade das células tentam ajustar sua direção (dado pelo ângulo ) com a de . Então atribuímos a ela uma força restauradora, caracterizada pela equação diferencial:
é o tempo de relaxação e é o ruído branco gaussiano da autopropulsão. Usando a fórmula do produto vetorial entre e :
Chegamos, assim, na seguinte expressão para o ângulo :
Onde é o vetor unitário perpendicular ao plano de movimento dos queratócitos. Deste modo, para atualizarmos o valor de basta utilizarmos a seguinte expressão:
Cálculo das forças intercelulares
As forças entre os queratócitos são funções que dependem apenas das distâncias entre os centros de massa de cada um. Os dois principais critérios para a elaboração das forças foram: (i) As células devem ter um volume bem definido e apenas interagirem com os vizinhos mais próximos e (ii) para um certo valor de as células não devem mais interagirem. Assim considerou-se os queratócitos com um volume de raio , onde sofrem uma força repulsiva até uma distância , uma força atrativa entre as distâncias e e zero para maiores que . Então temos a seguinte forma:
Onde , , é o máximo valor da força repulsiva para e é o máximo valor da força atrativa para (Como pode ser visto na figura 4).
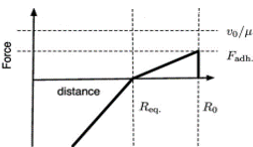
Com isso a dinâmica dos queratócitos está completa.
Resultados
Finalizado a dinâmica das células utilizou-se um programa em Python para simular os queratócitos para três diferentes valores de ruído. Porque além de apresentar uma transição de fase cinética variando a densidade (Como mostrado no experimento), também há uma transição variando a intensidade do ruído, ou seja, a potência natural da autopropulsão. Com isso, dado o programa obteve-se as seguintes simulações:
Parâmetro de Ordem
Para visualizar a transição de fase cinética definiu-se um parâmetro de ordem onde é definido da seguinte maneira:
Neste parâmetro queremos basicamente medir o quão desordenado está o sistema. Então a ideia é somar vetorialmente as velocidades de cada célula - dividida pelos seus respectivos módulos, pois só nos interessa a direção - e normalizamos pela quantidade de células. Além disso, ainda se faz uma média temporal a fim de melhorar ainda mais a medida. Tal tipo de parâmetro foi definido porque, por exemplo, se o sistema está em um estado dito desordenado esperamos os queratócitos vagando em direção aparentemente aleatórias, logo se somarmos as velocidades a resultante será um vetor nulo, e o valor de tenderá a zero. Já quando o sistema estiver um estado dito ordenado, as células estarão em um movimento coletivo, ou seja, o módulo da velocidade resultante será diferente de zero, por conseguinte, o valor de tenderá a 1.
Resultado do Parâmetro de ordem
Antes de calcular o parâmetro fazendo a média temporal, temos que observar o gráfico da evolução temporal de (fazendo uso do programa em Python Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \it{Evolucao \;temporal\; do \;parâmetro \;de \;ordem\;}} ):
Nota-se que há um transiente, com isso então para realizar o cálculo da média apenas utiliza-se os valores de para a cima de 50 interações a fim de desprezar o transiente e obter uma melhor média.
Feito isto, com um outro programa em Python temos o resultado obtido a partir das simulações:
Assim, nota-se que se obteve um gráfico característico de uma transição de fase confirmando o que havíamos esperado. Fazendo uso de mais partículas pode-se chegar em um gráfico como o feito em SZABÓ et al (2006) [1].
Códigos
Modelo de Szabó - Simulação dos queratócitos
Modelo de Szabó - Evolução temporal do parâmetro de ordem
Modelo de Szabó - Transição de fase










![{\displaystyle {\frac {d\theta _{i}^{n}(t)}{dt}}={\frac {1}{\tau }}arcsin\left[\left({\textbf {n}}_{i}(t){\frac {{\textbf {v}}_{i}(t_{k})}{|{\textbf {v}}_{i}(t_{k})|}}\right)\cdot {\textbf {e}}_{z}\right]+\xi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a8644464080bda002162a917bee8b21695263e)