Pêndulos Estocásticos: mudanças entre as edições
| (46 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 69: | Linha 69: | ||
</center> | </center> | ||
mas <math>\xi(t)dt</math> é o incremento do processo de Wiener | mas <math>\xi(t)dt</math> é o incremento do processo de Wiener <math> \left (W(t) = \int_0^t \xi(t')dt' \right ) </math>, então | ||
<center> | <center> | ||
| Linha 138: | Linha 138: | ||
* Realizar um ajuste linear nos dados <math>\langle E \rangle_t \times t</math> para obter o coeficiente angular, que corresponde a potência média gerada pelo ruído (<math>\bar P</math>). | * Realizar um ajuste linear nos dados <math>\langle E \rangle_t \times t</math> para obter o coeficiente angular, que corresponde a potência média gerada pelo ruído (<math>\bar P</math>). | ||
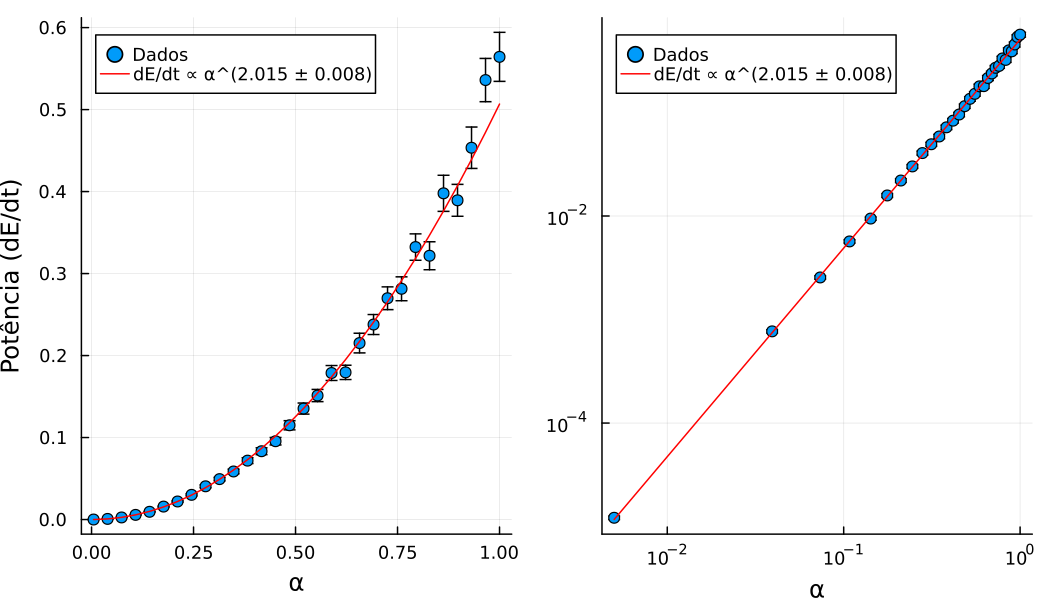
Com as simulações executadas, foi realizado o gráfico <math>\bar P \times \alpha</math>. Notamos que os dados se alinham em linha reta com os eixos em escala logarítmica, ou seja, os mesmos seguem uma lei de potência <math>\bar P = ae^{b \alpha}</math>, então foi realizado outro ajuste linear para | Com as simulações executadas, foi realizado o gráfico <math>\bar P \times \alpha</math>. Notamos que os dados se alinham em linha reta com os eixos em escala logarítmica, ou seja, os mesmos seguem uma lei de potência <math>\bar P = ae^{b \alpha}</math>, então foi realizado outro ajuste linear para encontrar o expoente <math>b</math>, a figura a seguir ilustra os dados e os resultados do ajuste: | ||
[[Arquivo:Power.png|frame|center|Potência em função do ruído (<math>\alpha</math>). O painel da esquerda possui eixos em escala linear e o da direita em escala logarítmica.]] | [[Arquivo:Power.png|frame|center|Potência em função do ruído (<math>\alpha</math>). O painel da esquerda possui eixos em escala linear e o da direita em escala logarítmica.]] | ||
| Linha 151: | Linha 151: | ||
[[Arquivo:Energy_beta_example.png|frame|center|Energia mecânica média em função do tempo com amortecimento.]] | [[Arquivo:Energy_beta_example.png|frame|center|Energia mecânica média em função do tempo com amortecimento.]] | ||
claramente o comportamento neste caso é diferente do observado sem amortecimento, agora a | claramente o comportamento neste caso é diferente do observado sem amortecimento, agora a energia aumenta até um certo valor e permanece nele. Para explorar este novo fenômeno, os seguintes passos foram feitos para cada valor de <math>\beta = 0.01, 0.1, 0.2 </math>: | ||
* Para diversos valores de <math>\alpha</math>, executar 700 simulações até a energia estabilizar, salvando a média da energia entre as simulações. | * Para diversos valores de <math>\alpha</math>, executar 700 simulações até a energia estabilizar, salvando a média da energia entre as simulações. | ||
| Linha 203: | Linha 203: | ||
os seguintes valores foram utilzados | os seguintes valores foram utilzados | ||
* g = l = 1 | * <math> g = l = 1 </math> | ||
* k = 1.1 | * <math> k = 1.1 </math> | ||
No gráfico da esquerda, o ângulo oscilou um pouco e permaneceu em 0, já no outro, eventualmente, o ângulo explodiu. Abaixo segue uma animação dessa situação, mas com <math>\alpha=1</math> para o pêndulo sair do equilíbrio mais rápido | No gráfico da esquerda, o ângulo oscilou um pouco e permaneceu em 0, já no outro, eventualmente, o ângulo explodiu. Abaixo segue uma animação dessa situação, mas com <math>\alpha=1</math> para o pêndulo sair do equilíbrio mais rápido | ||
| Linha 210: | Linha 210: | ||
[[Arquivo:Inverted_going_crazy.gif|frame|center|Pêndulo invertido partindo do equilíbrio com ruído.]] | [[Arquivo:Inverted_going_crazy.gif|frame|center|Pêndulo invertido partindo do equilíbrio com ruído.]] | ||
== Pêndulo Duplo | == Pêndulo Duplo == | ||
[[Arquivo:Pendulo.gif|thumb|upright=2|center|Pêndulo | O pêndulo duplo estocástico é um sistema dinâmico que combina a complexidade intrínseca do pêndulo duplo com a introdução de elementos de aleatoriedade ou incerteza, tornando o comportamento do sistema ainda mais imprevisível e caótico. O pêndulo duplo em si é um exemplo clássico de um sistema caótico, onde pequenas variações nas condições iniciais podem resultar em trajetórias drasticamente diferentes. Quando um termo estocástico é adicionado, por exemplo, na forma de uma força externa aleatória ou de flutuações nos parâmetros do sistema, a análise e a previsão do movimento se tornam desafiadoras. | ||
[[Arquivo:Pendulo.gif|thumb|upright=2|center|Pêndulo duplo não estocástico.]] | |||
=== Equação de movimento === | === Equação de movimento === | ||
O pêndulo duplo consiste em dois pêndulos acoplados, onde o segundo pêndulo está suspenso na extremidade do primeiro. As equações de movimento para o pêndulo duplo sem termos estocásticos podem ser derivadas utilizando as equações de Lagrange, considerando as coordenadas angulares <math> \theta_1 </math> e <math> \theta_2 </math> como as variáveis generalizadas e são dadas por: | O pêndulo duplo consiste em dois pêndulos acoplados, onde o segundo pêndulo está suspenso na extremidade do primeiro. As equações de movimento para o pêndulo duplo sem termos estocásticos podem ser derivadas utilizando as equações de Lagrange, considerando as coordenadas angulares <math> \theta_1 </math> e <math> \theta_2 </math> como as variáveis generalizadas e são dadas por: | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 227: | Linha 230: | ||
</math> | </math> | ||
</center> | </center> | ||
Mantendo <math> m_{1} </math>, <math> m_{2} </math>, <math> l </math>, e <math> g </math> fixos, defina : | |||
<center> | <center> | ||
| Linha 234: | Linha 238: | ||
</math> | </math> | ||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 240: | Linha 245: | ||
</center> | </center> | ||
assim as equações dinâmicas | assim podemos escrever as equações dinâmicas de maneira mais compacta, | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 246: | Linha 252: | ||
</math> | </math> | ||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 252: | Linha 259: | ||
</center> | </center> | ||
Suponha que haja um força externa ruidosa agindo sobre <math> m_1 </math> tal que, <math> F^{r}_{1} = \sigma_1 \xi_1 (t) </math>, onde <math> \sigma_1 </math> além de representar a intensidade do ruído gaussiano, terá consigo todas as constantes agrupadas, suponha o mesmo para <math> m_2 </math>. Assim as equações de movimento se tornam: | |||
<center> | <center> | ||
<math> | <math> | ||
| Linha 258: | Linha 266: | ||
</math> | </math> | ||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 263: | Linha 272: | ||
</math> | </math> | ||
</center> | </center> | ||
Portanto, obtemos um sistema de equações diferencias estocásticas com ruído gaussiano aditivo. | |||
=== Método de integração === | === Método de integração === | ||
Para a integração numérica desse sistema utilizaremos o método Runge-Kutta 4. Seja <math> \omega_{i} = \dot{\theta_{i}} </math> o sistema | |||
Para a integração numérica desse sistema utilizaremos o método Runge-Kutta 4. Seja <math> \omega_{i} = \dot{\theta_{i}} </math>, reduzindo a ordem das equações diferencias, o sistema se torna: | |||
<center> | <center> | ||
<math> | <math> | ||
\omega_{1} = \dot{\theta_{1}} | \begin{aligned} | ||
\omega_{1} &= \dot{\theta_{1}} \\ | |||
\dot \omega_1 &= f_{1}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2}) + \sigma_{1} \xi_{1} (t) \\ | |||
\omega_{2} &= \dot{\theta_{2}}\\ | |||
\dot \omega_2 &= f_{2}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2}) + \sigma_{2} \xi_{2} (t) | |||
\dot \omega_1 = f_{1}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2}) + \sigma_{1} \xi_{1} (t) | \end{aligned} | ||
\omega_{2} = \dot{\theta_{2}} | |||
\dot \omega_2 = f_{2}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2}) + \sigma_{2} \xi_{2} (t) | |||
</math> | </math> | ||
</center> | </center> | ||
| Linha 291: | Linha 294: | ||
<center> | <center> | ||
<math> | <math> | ||
\omega_{1}dt = d{\theta_{1}} | \begin{aligned} | ||
\omega_{1}dt &= d{\theta_{1}} \\ | |||
d \omega_1 &= f_{1}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2})dt + \sigma_{1} dW_{1}(t)\\ | |||
\omega_{2}dt &= d{\theta_{2}}\\ | |||
d \omega_2 &= f_{2}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2})dt + \sigma_{2} dW_{2}(t) | |||
d \omega_1 = f_{1}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2})dt + \sigma_{1} dW_{1}(t) | \end{aligned} | ||
\omega_{2}dt = d{\theta_{2}} | |||
d \omega_2 = f_{2}(\theta_{1}, \omega_{1}, \theta_{2}, \omega_{2})dt + \sigma_{2} dW_{2}(t) | |||
</math> | </math> | ||
</center> | </center> | ||
onde <math> dW_{i}(t) = \xi_{i}(t)dt </math> é o incremento do processo de Wiener. Discretizando as equações diferencias e aplicando o método RK4, obtemos: | onde <math> dW_{i}(t) = \xi_{i}(t)dt </math> é o incremento do processo de Wiener. Discretizando as equações diferencias e aplicando o método RK4, obtemos: | ||
<center> | <center> | ||
<math> | <math> | ||
| Linha 328: | Linha 322: | ||
</center> | </center> | ||
para <math> \omega_2 </math> e <math> \theta_2 </math> . | novamente, <math> R_{G} </math> é uma amostra de distribuição gaussiana de média 0 e variância 1. É completamente análogo para <math> \omega_2 </math> e <math> \theta_2 </math>. Utilizamos o RK4 pois necessitávamos de um alta precisão no cálculos por se tratar de um sistema caótico, simulações feitas sem o ruído externo mostram oscilações na energia total da ordem de <math> 10^{-4} </math>, o que se espera de um método de quarta ordem. | ||
=== Retrato de fase === | === Retrato de fase === | ||
O retrato de fase é uma ferramenta gráfica que representa a evolução do sistema dinâmico em termos de variáveis de estado, geralmente o ângulo <math> \theta </math> e a velocidade angular <math> \omega </math> no caso de sistemas oscilatórios como pêndulos. Este tipo de gráfico permite uma visualização clara de como o sistema se comporta ao longo do tempo, identificando padrões, ciclos limitados, ou comportamentos caóticos. Quando o sistema é perturbado por ruídos, o retrato de fase mostrará como essas perturbações afetam a trajetória do sistema, introduzindo variações que podem transformar oscilações regulares em comportamentos mais complexos ou caóticos. | |||
==== Caso 1 : Ruído em θ₁ ==== | |||
[[Arquivo:Pendulo_fase_estocastico_theta1.gif|thumb|upright=2|center|Pêndulo duplo estocástico com ruído branco em <math> \theta_1 </math>, <math> \sigma = 0.5 </math> e <math> dt = 0.01 </math>.]] | |||
Neste cenário, o ruído afeta apenas o primeiro pêndulo, introduzindo variações na trajetória de <math> \theta_1 </math> e <math> \omega_1 </math>. O retrato de fase para <math> \theta_1 </math> versus <math> \omega_1 </math> mostra uma dispersão maior em comparação com <math> \theta_2 </math> versus <math> \omega_2 </math>, onde o comportamento pode permanecer mais regular se não houver acoplamento forte entre os pêndulos. | |||
==== Caso 2 : Ruído em θ₂ ==== | |||
[[Arquivo:Pendulo_fase_estocastico_theta2.gif|thumb|upright=2|center|Pêndulo duplo estocástico com ruído branco em <math> \theta_2 </math>, <math> \sigma = 0.5 </math> e <math> dt = 0.01 </math>.]] | |||
Com ruído aplicado apenas ao segundo pêndulo, <math> \theta_2 </math> e <math> \omega_2 </math> exibem uma dispersão significativa no retrato de fase, enquanto <math> \theta_1 </math> versus <math> \omega_1 </math> pode permanecer mais regular. A interação entre os pêndulos, no entanto, pode ainda transferir alguma irregularidade de <math> \theta_2 </math> para <math> \theta_1 </math>. | |||
==== Caso 3 : Ruídos Iguais em θ₁ e θ₂ ==== | |||
[[Arquivo:Pendulo_fase_estocastico_theta12eq.gif|thumb|upright=2|center|Pêndulo duplo estocástico com ruído branco igual em <math> \theta_1 </math> e <math> \theta_2 </math>, <math> \sigma = 0.5 </math> e <math> dt = 0.01 </math>.]] | |||
Quando o mesmo ruído é aplicado a ambos os pêndulos, as trajetórias de <math> \theta_1 </math> e <math> \theta_2 </math> serão correlacionadas, resultando em retratos de fase que se comportam de maneira similar. Pode-se observar um padrão sincrônico onde ambos os pêndulos respondem de maneira similar às perturbações, mantendo uma relação quase constante entre <math> \theta_1 </math> e <math> \theta_2 </math>. | |||
==== Caso 4 : Ruídos Diferentes em θ₁ e θ₂ ==== | |||
[[Arquivo:Pendulo_fase_estocastico_theta12.gif|thumb|upright=2|center|Pêndulo duplo estocástico com ruídos brancos diferentes em <math> \theta_1 </math> e <math> \theta_2 </math>, <math> \sigma = 0.5 </math> e <math> dt = 0.01 </math>.]] | |||
Aplicar ruídos diferentes a cada pêndulo pode resultar no comportamento mais complexo e caótico. As trajetórias de <math> \theta_1 </math> versus <math> \omega_1 </math> e <math> \theta_2 </math> versus <math> \omega_2 </math> podem mostrar padrões bastante distintos, refletindo a falta de correlação entre as perturbações. Esse cenário pode conduzir a uma maior imprevisibilidade no comportamento do sistema como um todo, especialmente em regiões do espaço de fase onde os pêndulos interagem fortemente. | |||
=== Energia === | |||
Afim de compreender como se comporta a energia mecânica do pêndulo duplo com o acréscimo de uma força externa ruidosa, vamos analisar 4 sistemas de pêndulo duplo onde o ruído é adicionado de alguma maneira específica. Alguns pontos a serem observados são : | |||
* Em todas as simulações fixamos <math> m_{1} </math> = <math> m_{2} </math> = <math> l_{1} </math> = <math> l_{2} </math> = <math> 1 </math> ; | |||
* As condições inicias serão sempre <math> \theta_{1}(t=0) </math> = <math> \theta_{2}(t=0) </math> = <math> \omega_{1}(t=0) </math> = <math> \omega_{2}(t=0) </math> = <math> 0 </math> ; | |||
* Em todas as simulações o passo temporal é <math> dt = 10^{-3} </math> ; | |||
* Nos casos onde são calculadas grandezas médias, foram realizadas 100 simulações. | |||
==== Caso 1 : Ruído em θ₁ ==== | |||
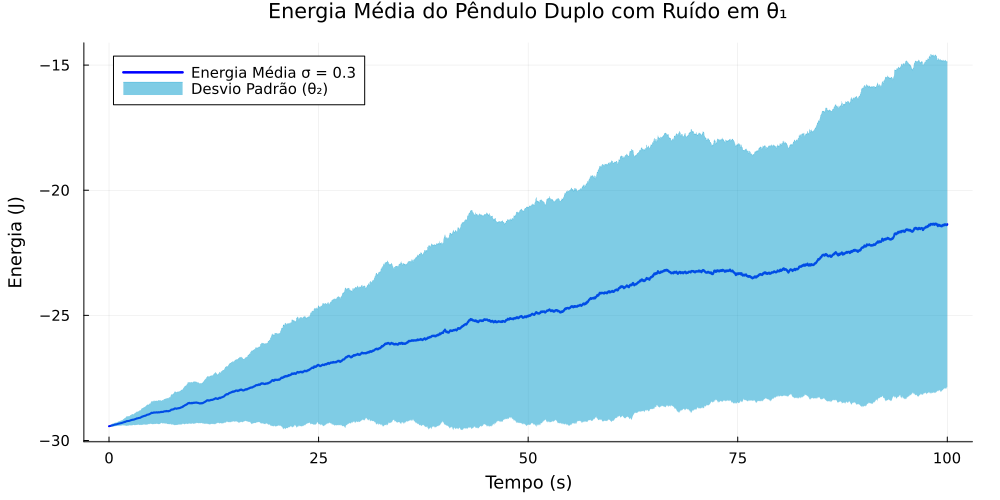
Nesta simulação, uma força ruidosa foi introduzida exclusivamente na equação dinâmica para <math> \theta_{1} </math>. A análise da energia mecânica média revela um aumento linear ao longo do tempo, indicando que, em média, o ruído está efetivamente injetando energia no sistema. | |||
[[Arquivo:energia_media_theta1.png|thumb|upright=0.0|center|Energia mecânica média do pêndulo duplo sujeito a um ruído em <math> \theta_{1} </math>.|700px]] | |||
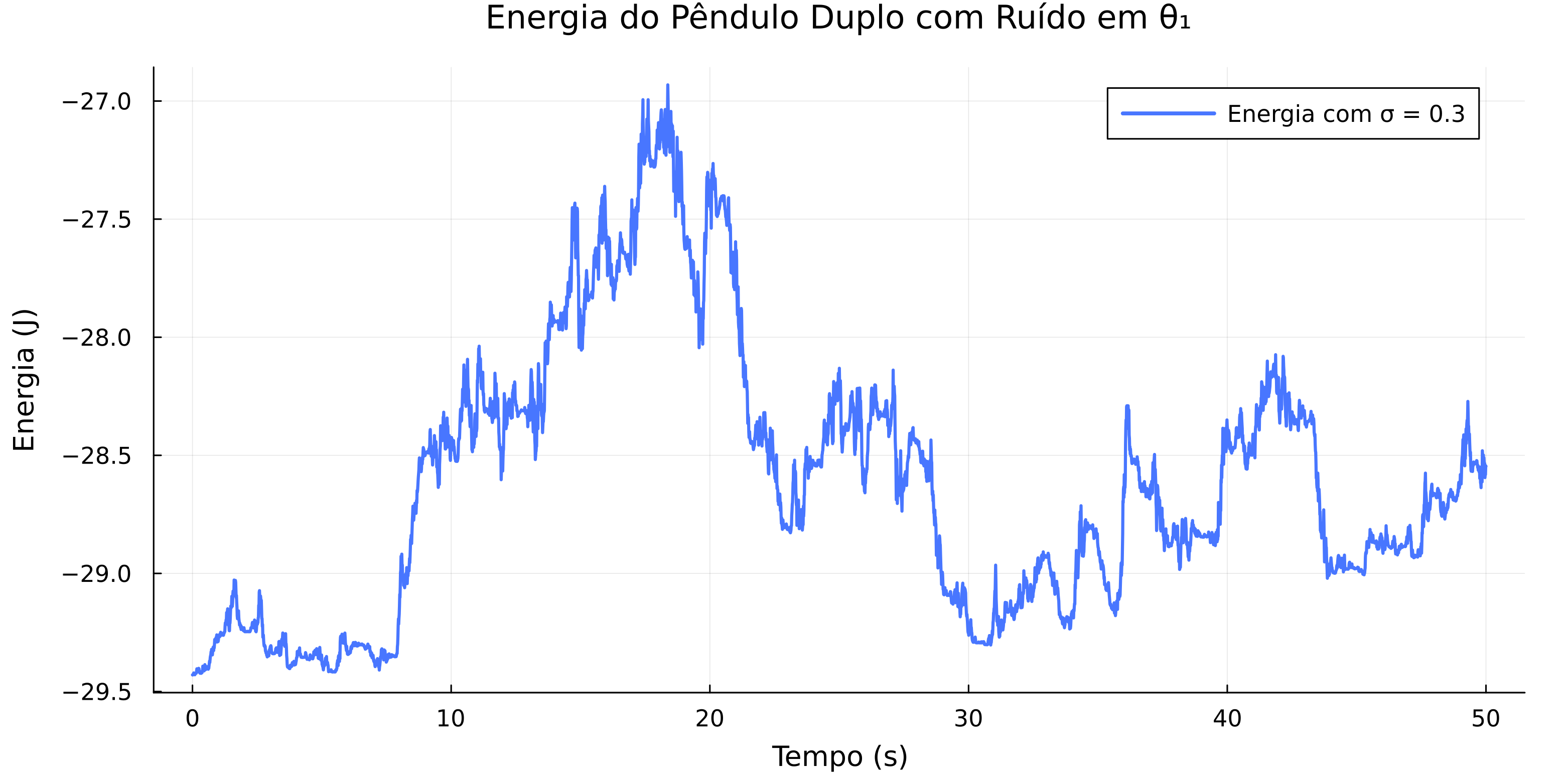
No entanto, o desvio padrão dessa energia é extremamente elevado, o que sugere que, em certos momentos, a quantidade de energia injetada pelo ruído é quase nula. Esse comportamento pode ser exemplificado pelo fenômeno de ressonância destrutiva, como ilustrado no seguinte exemplo: | |||
<br style="clear:both;">[[Arquivo:exemplo_energia_destrutiva.png|thumb|upright=0.0|left|Energia mecânica do pêndulo duplo sujeito a um ruído em <math> \theta_{1} </math>.|700px]] | |||
[[Arquivo:exemplo_destrutiva_theta1.gif|thumb|upright=0.0|center|Simulação do pêndulo duplo sujeito a um ruído em <math> \theta_{1} </math>.|350px]] <br style="clear:both;"> | |||
Por volta dos 30 segundos de simulação, é possível observar uma ressonância destrutiva, causada pela interação entre o ruído aplicado e a inércia do sistema, que resulta em uma diminuição temporária da energia mecânica. | |||
==== Caso 2 : Ruído em θ₂ ==== | |||
Nesta simulação, uma força ruidosa foi introduzida exclusivamente na equação dinâmica para <math> \theta_{2} </math>. Observa-se, de maneira semelhante ao caso anterior, um aumento linear da energia mecânica média do sistema. | |||
[[Arquivo:energia_media_theta2.png|thumb|upright=0.0|center|Energia mecânica média do pêndulo duplo sujeito a um ruído em <math> \theta_{2} </math>.|700px]] | |||
Embora essa situação pareça análoga ao caso 1, uma análise comparativa entre a energia adicionada em ambos os casos revela diferenças importantes: | |||
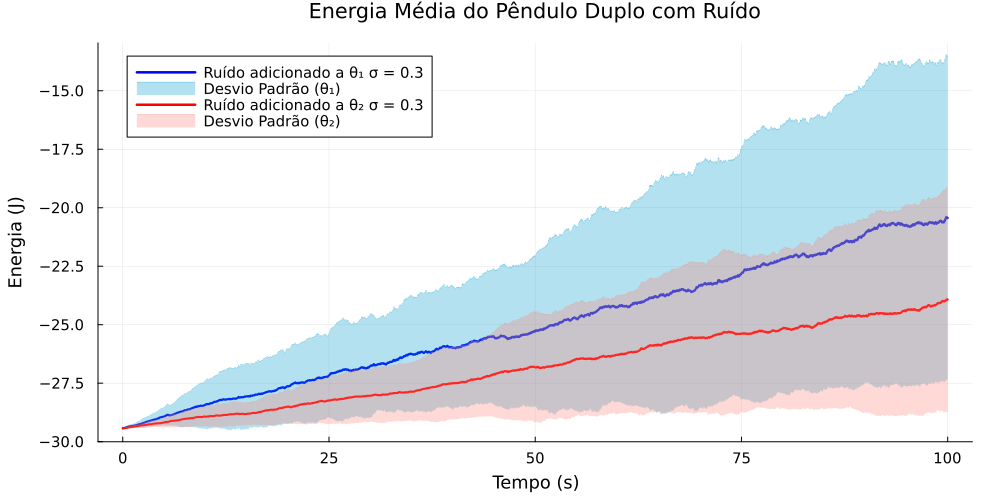
[[Arquivo:energia_media_comparacao.png|thumb|upright=0.0|center|Comparação entre a energia mecânica do pêndulo no caso 1 e 2.|700px]] | |||
Os resultados mostram que, em média, a introdução de ruído no primeiro pêndulo do sistema provoca um aumento mais significativo na energia mecânica média em comparação com a aplicação de ruído apenas no segundo pêndulo. | |||
==== Caso 3 : Ruídos em θ₁ e θ₂ ==== | |||
Nessa simulação faremos a comparação entre dois casos : | |||
* Adicionaremos o mesmo ruído em <math> \theta_{1} </math> e <math> \theta_{2} </math>; | |||
* Adicionaremos ruídos diferentes em <math> \theta_{1} </math> e <math> \theta_{2} </math>. | |||
A seguir, analisamos a energia mecânica média em ambos os casos : | |||
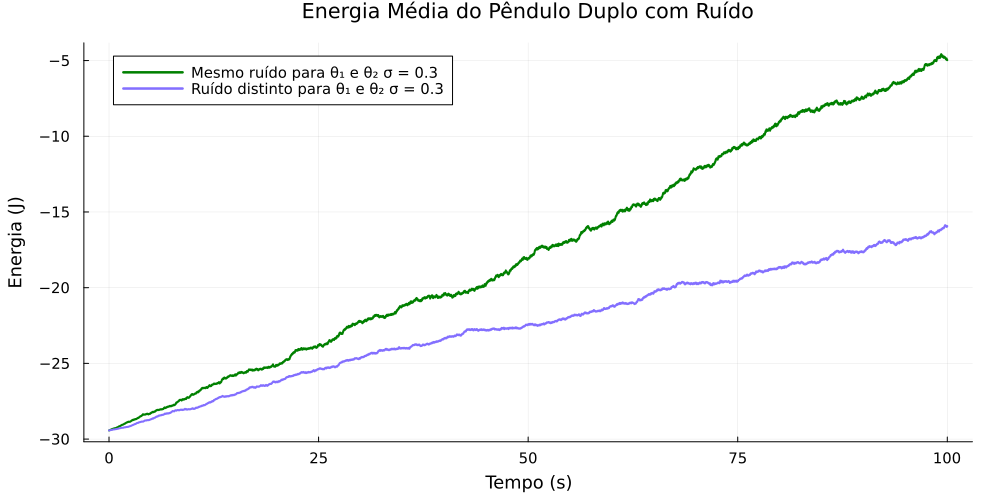
[[Arquivo:energia_media_comparacao_ruidos.png|thumb|upright=0.0|center|Comparação entre a energia mecânica média do pêndulo quando há uma simetria no ruído e quando não há.|700px]] | |||
Os resultados mostram que, em média, a aplicação de ruídos simétricos em <math> \theta_{1} </math> e <math> \theta_{2} </math> leva a um aumento mais | |||
pronunciado da energia mecânica. Esse efeito é atribuído a uma ressonância construtiva entre os ruídos idênticos, amplificando a energia do sistema. Em contraste, a aplicação de ruídos distintos provoca uma competição entre forças momentaneamente opostas, resultando em uma ressonância destrutiva que atenua o aumento da energia. Apresentamos também como se comporta a energia mecânica média para diferentes intensidades de ruído: | |||
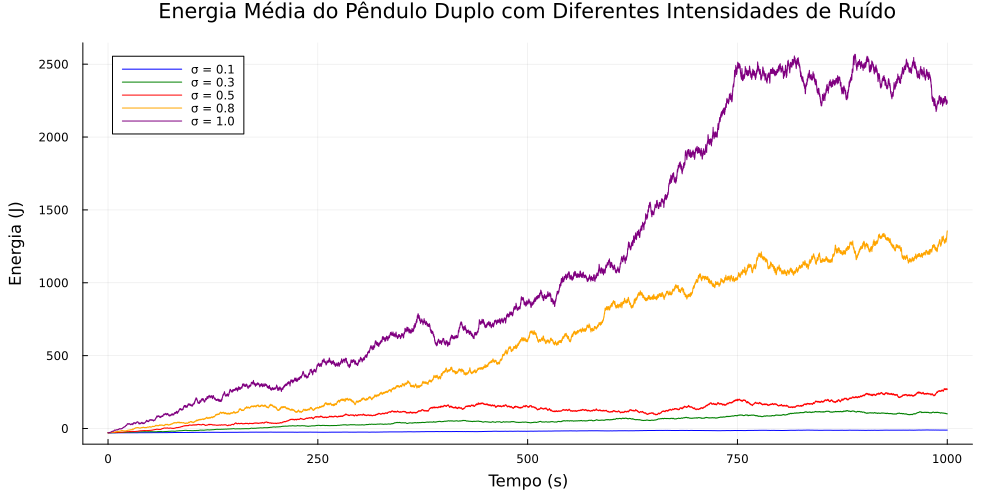
<br style="clear:both;">[[Arquivo:Iguais-energia_vs_ruido.png|thumb|upright=0.0|left|Energia mecânica do pêndulo duplo sujeito ao mesmo ruído em <math> \theta_{1} </math> e <math> \theta_{2} </math>.|700px]] | |||
[[Arquivo:Diferentes-energia_vs_ruido.png|thumb|upright=0.0|center|Energia mecânica do pêndulo duplo sujeito a um ruído em <math> \theta_{1} </math> e outro em <math> \theta_{2} </math>.|700px]] <br style="clear:both;"> | |||
Essas simulações foram repetidas 50 vezes. | |||
== Referências == | |||
# NASCIMENTO, Luciano. A dinâmica lagrangeana do pêndulo duplo. Educ.&Tecnol., Belo Horizonte, v. 22, n. 1, p. 64-71, jan./abr. 2017. | |||
Edição atual tal como às 15h09min de 22 de agosto de 2024
Grupo : Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa.
Pêndulo Simples
Equação de movimento
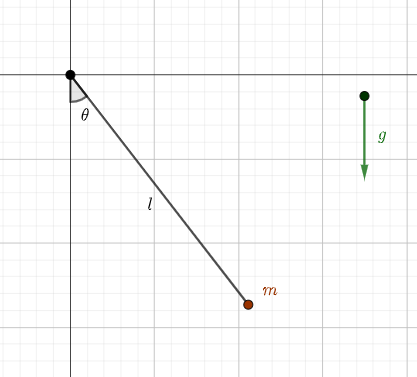
Primeiramente vamos inserir ruído em um pêndulo simples, que é constituído de uma barra de comprimento , sem massa e rígida que contém uma massa pontual em sua ponta, conforme ilustrado na figura a seguir.
Considerando que o pêndulo está sob o efeito da gravidade e se encontra submerso em um fluido viscoso (como o ar), tal que a força de resistência que atua na massa é , a equação de movimento é dada por:
Vamos supor que existe uma força ruidosa atuando em , tal que sua componente tangencial () pode ser modelada por um ruído branco gaussiano da seguinte forma
em que é a intensidade do ruído. é caracterizado pelas seguintes propriedades:
Adicionando essa nova força nas equações de movimento, ficamos com
A partir de agora, por questão de simplicidade, vamos supor que , então
Método de integração
Vamos montar um método para integrar o sistema no tempo. Primeiramente vamos dividir a equação em duas equações diferencias de primeira ordem, introduzindo a variável , então ficamos com o seguinte sistema
que pode ser escrito na forma diferencial
mas é o incremento do processo de Wiener , então
Discretizando o tempo e lembrando que a densidade de probabilidade de transição de para tem desvio padrão igual a
em que é uma amostra de uma distribuição gaussiana com média 0 e variância 1, e o método de Euler foi utilizado para a parte determinística da equação.
Nas próximas seções será analisado a energia do sistema, e como o método de Euler não é muito bom para preservar a energia de sistemas conservativos, será utilizado o método preditor corretor (com adição do método de Heun para ) para a parte determinística da equação, que consiste nos seguintes passos:
- Calcular um theta intermediário:
- Com calcular um theta médio e utilizá-lo para obter um omega intermediário:
- Em que é a expressão do método de Euler visto logo acima.
- Recalcular theta utilizando um omega intermediário
- Recalcular omega com um theta intermediário atualizado
- OBS: No cálculo de e foi utilizado o mesmo .
Energia (Sem amortecimento)
Logo após terminar a implementação do método numérico, rapidamente notamos que a adição do ruído gera um aumento na energia mecânica do pêndulo (), vamos explorar esse fenômeno, sempre utilizando . Para ilustrar esse efeito, segue uma animação do pêndulo partindo do repouso na configuração de equilíbrio estável () com
Para realizar uma exploração quantitativa, o seguinte procedimento foi feito para vários valores de :
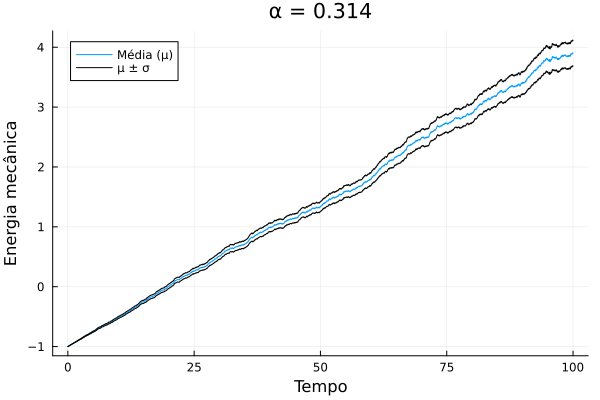
- Utilizando , integrar o sistema até , calculando e armazenando a energia em cada passo temporal. Repetir essa integração 700 vezes para fazer médias temporais. Como exemplo, segue os dados obtidos da energia em função do tempo (com a média temporal feita) para um determinado utilizado
- O gráfico nos indica que o ruído gera uma potência média sobre o pêndulo.
- Realizar um ajuste linear nos dados para obter o coeficiente angular, que corresponde a potência média gerada pelo ruído ().
Com as simulações executadas, foi realizado o gráfico . Notamos que os dados se alinham em linha reta com os eixos em escala logarítmica, ou seja, os mesmos seguem uma lei de potência , então foi realizado outro ajuste linear para encontrar o expoente , a figura a seguir ilustra os dados e os resultados do ajuste:
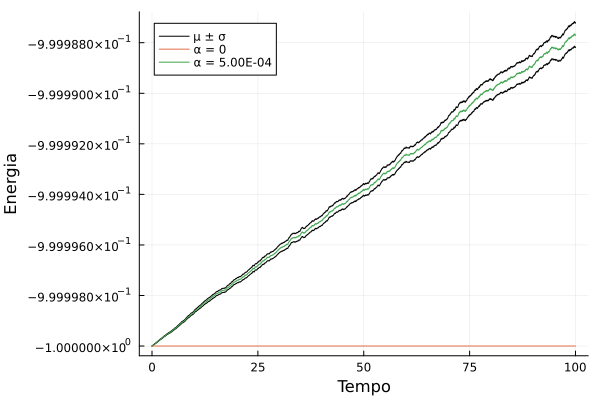
Portanto, aumenta, aproximadamente, de forma quadrática com . Por fim, gostaríamos de mostrar que mesmo para muito pequeno, ainda existe energia sendo injetada no sistema com taxa constante, e isso não é um artefato da simulação. Para tal, foram realizadas 700 simulações com e os resultados foram comparados com
Energia (Com amortecimento)
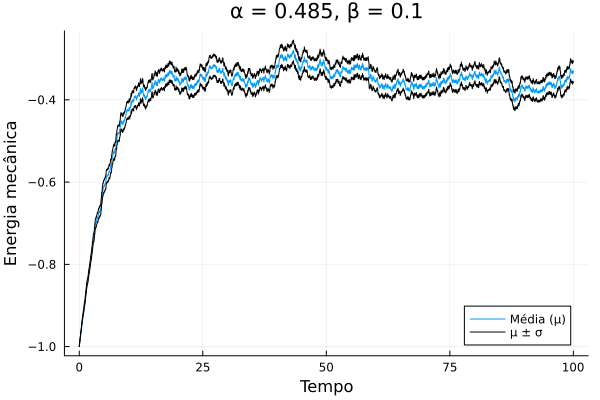
Até o momento, o amortecimento foi negligenciado. Vamos, então, introduzi-lo e rodar várias simulações (700, neste caso) e observar como a média temporal da energia evolui ao longo do tempo, assim como foi feita na seção anterior. Utilizando e foi obtido o seguinte resultado
claramente o comportamento neste caso é diferente do observado sem amortecimento, agora a energia aumenta até um certo valor e permanece nele. Para explorar este novo fenômeno, os seguintes passos foram feitos para cada valor de :
- Para diversos valores de , executar 700 simulações até a energia estabilizar, salvando a média da energia entre as simulações.
- Para cada conjunto de dados gerados por um determinado , selecionar um intervalo de tempo onde a energia está estabilizada e calcular a sua média ().
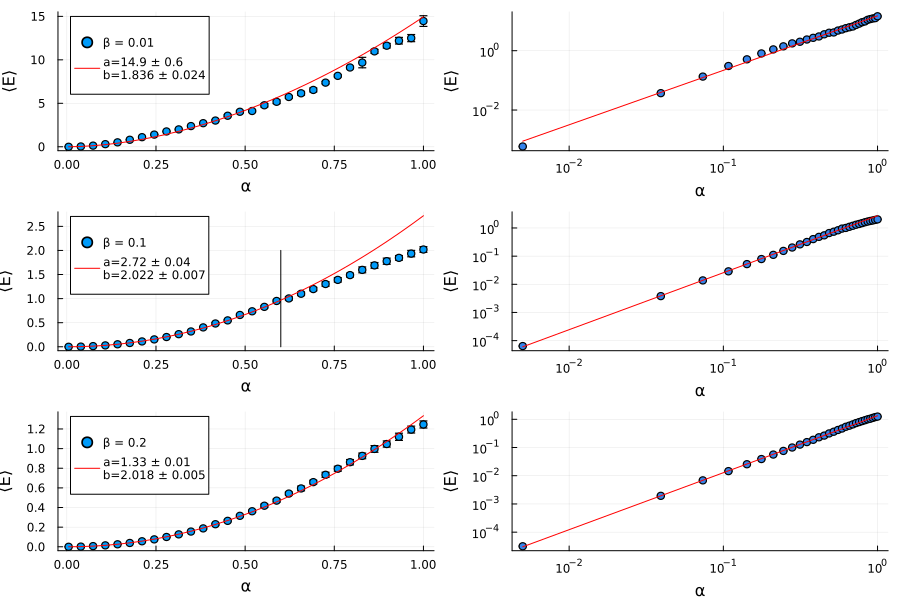
Produzindo o gráfico de obtemos
as linhas vermelhas são os melhores ajustas de leis de potência na forma . Para os dados utilizados no ajuste foram apenas até (indicado pela reta preta vertical no gráfico), pois após esse limite, a lei de potência deixa de ser um ótimo ajuste. É chamativo o fato de todos os coeficientes, independente de , serem aproximadamente 2.
Pêndulo invertido
O próximo pêndulo a ser considerado é um pêndulo invertido, que possui um potencial harmônico em seu ângulo, ou seja, um dos termos de sua energia potential é , sendo que agora é zero quando a haste está apontando para cima, conforme ilustrado na figura a seguir
Ainda, a base do pêndulo é livre para movimentar-se na direção vertical, é justamente nesse local onde será adicionado uma força ruidosa. A equação de movimento neste caso é
O primeiro termo vem da resistência do ar, o segundo se origina da gravidade e do deslocamento de e o último provém da "mola" em . Vamos supor que existe um vínculo mantendo a base fixa, mas o local onde o pêndulo é fixado pode se movimentar de forma aleatória na direção vertical, supondo que tal movimento pode ser modelado por ruído branco gaussiano, segue que . Introduzindo a variável , ficamos com os seguintes sistemas de equações na forma diferencial
Note que agora o ruído é multiplicativo, em contraste com o ruído aditivo dos pêndulos anteriores, para lidar com esta complicação, no momento da integração vamos utilizar um médio no argumento do seno que multiplica
Esse tipo de pêndulo é de grande interesse em algumas áreas, como na engenharia estrutural, pois uma coluna comprimida pode ser modelada como um pêndulo invertido com uma mola na base, o ruído da base pode representar um terremoto.
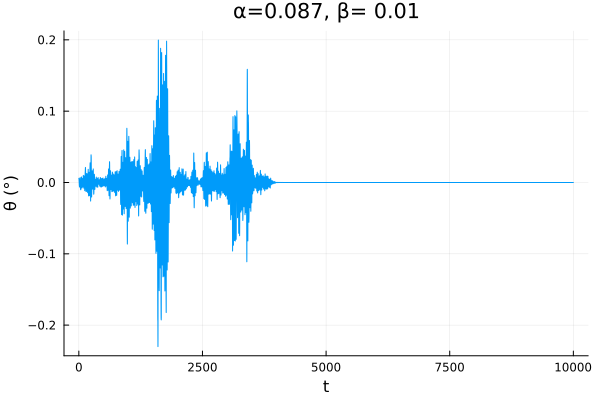
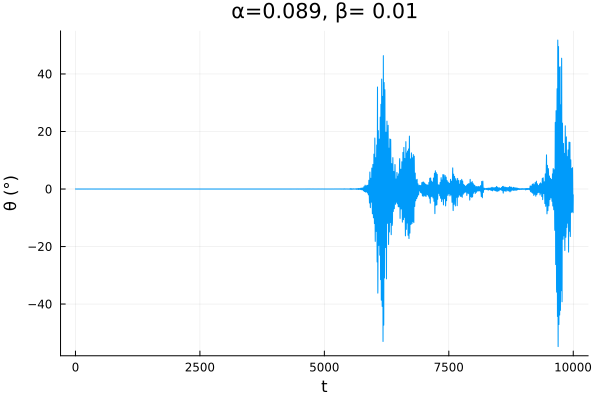
Uma questão interessante neste modelo é sobre a estabilidade da configuração quando é adicionado ruído e amortecimento. Se é grande o suficiente, sem ruído, o equilíbrio é estável, mas é possível sair dessa configuração adicionando ruído, cujo valor limite vai depender do amortecimento. Podemos demostrar isso integrando o sistema, partindo da condição inicial , com valores de muito próximos:
os seguintes valores foram utilzados
No gráfico da esquerda, o ângulo oscilou um pouco e permaneceu em 0, já no outro, eventualmente, o ângulo explodiu. Abaixo segue uma animação dessa situação, mas com para o pêndulo sair do equilíbrio mais rápido
Pêndulo Duplo
O pêndulo duplo estocástico é um sistema dinâmico que combina a complexidade intrínseca do pêndulo duplo com a introdução de elementos de aleatoriedade ou incerteza, tornando o comportamento do sistema ainda mais imprevisível e caótico. O pêndulo duplo em si é um exemplo clássico de um sistema caótico, onde pequenas variações nas condições iniciais podem resultar em trajetórias drasticamente diferentes. Quando um termo estocástico é adicionado, por exemplo, na forma de uma força externa aleatória ou de flutuações nos parâmetros do sistema, a análise e a previsão do movimento se tornam desafiadoras.
Equação de movimento
O pêndulo duplo consiste em dois pêndulos acoplados, onde o segundo pêndulo está suspenso na extremidade do primeiro. As equações de movimento para o pêndulo duplo sem termos estocásticos podem ser derivadas utilizando as equações de Lagrange, considerando as coordenadas angulares e como as variáveis generalizadas e são dadas por:
Mantendo , , , e fixos, defina :
assim podemos escrever as equações dinâmicas de maneira mais compacta,
Suponha que haja um força externa ruidosa agindo sobre tal que, , onde além de representar a intensidade do ruído gaussiano, terá consigo todas as constantes agrupadas, suponha o mesmo para . Assim as equações de movimento se tornam:
Portanto, obtemos um sistema de equações diferencias estocásticas com ruído gaussiano aditivo.
Método de integração
Para a integração numérica desse sistema utilizaremos o método Runge-Kutta 4. Seja , reduzindo a ordem das equações diferencias, o sistema se torna:
na forma diferencial:
onde é o incremento do processo de Wiener. Discretizando as equações diferencias e aplicando o método RK4, obtemos:
novamente, é uma amostra de distribuição gaussiana de média 0 e variância 1. É completamente análogo para e . Utilizamos o RK4 pois necessitávamos de um alta precisão no cálculos por se tratar de um sistema caótico, simulações feitas sem o ruído externo mostram oscilações na energia total da ordem de , o que se espera de um método de quarta ordem.
Retrato de fase
O retrato de fase é uma ferramenta gráfica que representa a evolução do sistema dinâmico em termos de variáveis de estado, geralmente o ângulo e a velocidade angular no caso de sistemas oscilatórios como pêndulos. Este tipo de gráfico permite uma visualização clara de como o sistema se comporta ao longo do tempo, identificando padrões, ciclos limitados, ou comportamentos caóticos. Quando o sistema é perturbado por ruídos, o retrato de fase mostrará como essas perturbações afetam a trajetória do sistema, introduzindo variações que podem transformar oscilações regulares em comportamentos mais complexos ou caóticos.
Caso 1 : Ruído em θ₁
Neste cenário, o ruído afeta apenas o primeiro pêndulo, introduzindo variações na trajetória de e . O retrato de fase para versus mostra uma dispersão maior em comparação com versus , onde o comportamento pode permanecer mais regular se não houver acoplamento forte entre os pêndulos.
Caso 2 : Ruído em θ₂
Com ruído aplicado apenas ao segundo pêndulo, e exibem uma dispersão significativa no retrato de fase, enquanto versus pode permanecer mais regular. A interação entre os pêndulos, no entanto, pode ainda transferir alguma irregularidade de para .
Caso 3 : Ruídos Iguais em θ₁ e θ₂
Quando o mesmo ruído é aplicado a ambos os pêndulos, as trajetórias de e serão correlacionadas, resultando em retratos de fase que se comportam de maneira similar. Pode-se observar um padrão sincrônico onde ambos os pêndulos respondem de maneira similar às perturbações, mantendo uma relação quase constante entre e .
Caso 4 : Ruídos Diferentes em θ₁ e θ₂
Aplicar ruídos diferentes a cada pêndulo pode resultar no comportamento mais complexo e caótico. As trajetórias de versus e versus podem mostrar padrões bastante distintos, refletindo a falta de correlação entre as perturbações. Esse cenário pode conduzir a uma maior imprevisibilidade no comportamento do sistema como um todo, especialmente em regiões do espaço de fase onde os pêndulos interagem fortemente.
Energia
Afim de compreender como se comporta a energia mecânica do pêndulo duplo com o acréscimo de uma força externa ruidosa, vamos analisar 4 sistemas de pêndulo duplo onde o ruído é adicionado de alguma maneira específica. Alguns pontos a serem observados são :
- Em todas as simulações fixamos = = = = ;
- As condições inicias serão sempre = = = = ;
- Em todas as simulações o passo temporal é ;
- Nos casos onde são calculadas grandezas médias, foram realizadas 100 simulações.
Caso 1 : Ruído em θ₁
Nesta simulação, uma força ruidosa foi introduzida exclusivamente na equação dinâmica para . A análise da energia mecânica média revela um aumento linear ao longo do tempo, indicando que, em média, o ruído está efetivamente injetando energia no sistema.
No entanto, o desvio padrão dessa energia é extremamente elevado, o que sugere que, em certos momentos, a quantidade de energia injetada pelo ruído é quase nula. Esse comportamento pode ser exemplificado pelo fenômeno de ressonância destrutiva, como ilustrado no seguinte exemplo:
Por volta dos 30 segundos de simulação, é possível observar uma ressonância destrutiva, causada pela interação entre o ruído aplicado e a inércia do sistema, que resulta em uma diminuição temporária da energia mecânica.
Caso 2 : Ruído em θ₂
Nesta simulação, uma força ruidosa foi introduzida exclusivamente na equação dinâmica para . Observa-se, de maneira semelhante ao caso anterior, um aumento linear da energia mecânica média do sistema.
Embora essa situação pareça análoga ao caso 1, uma análise comparativa entre a energia adicionada em ambos os casos revela diferenças importantes:
Os resultados mostram que, em média, a introdução de ruído no primeiro pêndulo do sistema provoca um aumento mais significativo na energia mecânica média em comparação com a aplicação de ruído apenas no segundo pêndulo.
Caso 3 : Ruídos em θ₁ e θ₂
Nessa simulação faremos a comparação entre dois casos :
- Adicionaremos o mesmo ruído em e ;
- Adicionaremos ruídos diferentes em e .
A seguir, analisamos a energia mecânica média em ambos os casos :
Os resultados mostram que, em média, a aplicação de ruídos simétricos em e leva a um aumento mais pronunciado da energia mecânica. Esse efeito é atribuído a uma ressonância construtiva entre os ruídos idênticos, amplificando a energia do sistema. Em contraste, a aplicação de ruídos distintos provoca uma competição entre forças momentaneamente opostas, resultando em uma ressonância destrutiva que atenua o aumento da energia. Apresentamos também como se comporta a energia mecânica média para diferentes intensidades de ruído:
Essas simulações foram repetidas 50 vezes.
Referências
- NASCIMENTO, Luciano. A dinâmica lagrangeana do pêndulo duplo. Educ.&Tecnol., Belo Horizonte, v. 22, n. 1, p. 64-71, jan./abr. 2017.