Equação de Schrödinger Unidimensional: mudanças entre as edições
(Criou página com 'Conhecer o estado de uma partícula, na Mecânica Clássica, é saber, em um determinado momento, sua velocidade e sua posição. A partir destes valores, é possível determinar os seus futuros estados utilizando as relações fornecidas pelas Leis de Newton. Na Mecânica Quântica, porém, o estado físico não é mais caracterizado por uma quantidade discreta de valores numéricos, e sim, por uma função. A chamada Função de Onda, <math> \Psi </math>, nos informa a...') |
|||
| (15 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 2: | Linha 2: | ||
<math> -\frac{\hbar}{2m}\frac{\partial^2\Psi}{\partial x^2} + V(x)\Psi = i\hbar\frac{\partial\Psi}{\partial t} </math> | <math> -\frac{\hbar}{2m}\frac{\partial^2\Psi}{\partial x^2} + V(x)\Psi = i\hbar\frac{\partial\Psi}{\partial t} </math> | ||
== O Método De Crank-Nicolson== | |||
A fim de resolvê-la numericamente para diferentes tipos de potenciais, usou-se o Método de Crank-Nicolson de resolução de EDPs. Este método baseia-se em combinar os métodos explícito e implícito (com igual contribuição) para aumentar sua estabilidade. | A fim de resolvê-la numericamente para diferentes tipos de potenciais, usou-se o Método de Crank-Nicolson de resolução de EDPs. Este método baseia-se em combinar os métodos explícito e implícito (com igual contribuição) para aumentar sua estabilidade. | ||
| Linha 34: | Linha 36: | ||
Como dito, o Método de Crank-Nicolson é uma combinação dos métodos implícito e explícito, cada um tendo o mesmo peso de 1/2. Ao somarmos as duas equações (cada uma multiplicada por 0.5), ficaremos com a seguinte expressão: | Como dito, o Método de Crank-Nicolson é uma combinação dos métodos implícito e explícito, cada um tendo o mesmo peso de 1/2. Ao somarmos as duas equações (cada uma multiplicada por 0.5), ficaremos com a seguinte expressão: | ||
<math> \Psi_j^{n+1} = \Psi_{j}^{n} + \frac{i \Delta t}{4 \Delta x^2} (\Psi_{j+1}^{n} + \Psi_{j-1}^{n} - 2 \Psi_{j}^{n} + \Psi_{j+1}^{n+1} + \Psi_{j-1}^{n+1} - 2 \Psi_{j}^{n+1}) - \frac{i\Delta t}{2} V_j (\Psi_{j}^{n} + \Psi_{j}^{n+1})</math> | |||
que, ao reorganizarmos para isolar os | que, ao reorganizarmos para isolar os <math> \Psi_j^{n+1}</math>, resulta em: | ||
<math> \left(1+\frac{i \Delta t}{2 \Delta x^2}+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n+1} - \frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n+1} = \left(1-\frac{i \Delta t}{2 \Delta x^2}-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n} +\frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n}</math> | <math> \left(1+\frac{i \Delta t}{2 \Delta x^2}+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n+1} - \frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n+1} = \left(1-\frac{i \Delta t}{2 \Delta x^2}-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n} +\frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n}</math> | ||
Para resolver a equação em simultaneamente para ambos os tempos e em todos os pontos, escrevemos a equação em forma matricial: | |||
:<math> | |||
\begin{pmatrix} | |||
1 + 2b + \frac{i\Delta t V_j}{2} & -b & 0 & \cdots & 0 & 0 & 0\\ -b & 1 + 2b + \frac{i\Delta t V_j}{2} & -b &0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots& \vdots& \vdots \\ 0 & 0 & 0 & \cdots & 0 & -b & 1 + 2b + \frac{i\Delta t V_j}{2} | |||
\end{pmatrix} | |||
\begin{pmatrix} \Psi_1^{n+1} \\ \Psi_2^{n+1} \\ \vdots \\ \Psi_{j}^{n+1}\end{pmatrix} | |||
= | |||
\begin{pmatrix} | |||
1 - 2b - \frac{i\Delta t V_j}{2} & +b & 0 & \cdots & 0 & 0 & 0\\ +b & 1 - 2b - \frac{i\Delta t V_j}{2} & +b &0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots& \vdots& \vdots \\ 0 & 0 & 0 & \cdots & 0 & +b & 1 - 2b - \frac{i\Delta t V_j}{2} | |||
\end{pmatrix} | |||
\begin{pmatrix} \Psi_1^{n} \\ \Psi_2^{n} \\ \vdots \\ \Psi_{j}^{n} \end{pmatrix} ; | |||
</math> | |||
com | |||
<math> b=\frac{i \Delta t}{4 \Delta x^2}</math>. | |||
Podemos notar que a diferença entre as matrizes que multiplicam <math> \Psi_j^{n+1}</math> e <math> \Psi_j^{n}</math> é somente o sinal das componente imaginárias. Assim, a equação final pode ser escrita como: | |||
<math> A\Psi_j^{n+1} = A^*\Psi_j^{n}</math>, onde A é a matriz <math>\begin{pmatrix} | |||
1 + 2b + \frac{i\Delta t V_j}{2} & -b & 0 & \cdots & 0 & 0 & 0\\ -b & 1 + 2b + \frac{i\Delta t V_j}{2} & -b &0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots& \vdots& \vdots \\ 0 & 0 & 0 & \cdots & 0 & -b & 1 + 2b + \frac{i\Delta t V_j}{2} | |||
\end{pmatrix} </math> | |||
===Estabilidade do Método de Crank-Nicolson=== | |||
Para verificar a estabilidade, devemos primeiro olhar para a equação que define o método: | |||
<math> \left(1+\frac{i \Delta t}{2 \Delta x^2}+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n+1} - \frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n+1} = \left(1-\frac{i \Delta t}{2 \Delta x^2}-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + \frac{i \Delta t}{4 \Delta x^2}\Psi_{j+1}^{n} +\frac{i \Delta t}{4 \Delta x^2} \Psi_{j-1}^{n}</math> | |||
Para simplificar, chamaremos <math>\frac{i \Delta t}{4 \Delta x^2}</math> de b. Nesse caso, temos: | |||
<math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)\Psi_j^{n+1} - b\Psi_{j+1}^{n+1} - b\Psi_{j-1}^{n+1} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)\Psi_{j}^{n} + b\Psi_{j+1}^{n} +b\Psi_{j-1}^{n}</math> | |||
Definimos os Modos de Fourier: | |||
<math>\Psi_{j}^{n} \approx A^{n}e^{iqjh}</math> | |||
Assim, obtemos: | |||
<math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)A^{n+1}e^{iqjh}- bA^{n+1}e^{iq(j-1)h} - bA^{n+1}e^{iq(j+1)h} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)A^{n}e^{iqjh} + bA^{n}e^{iq(j-1)h} +bA^{n}e^{iq(j+1)h}</math> | |||
Dividindo tudo por <math>e^{iqjh}</math>: | |||
<math> \left(1+2b+\frac{i\Delta t}{2} V_j\right)A^{n+1}- bA^{n+1}e^{-iqh} - bA^{n+1}e^{iqh} = \left(1-2b-\frac{i\Delta t}{2} V_j\right)A^{n} + bA^{n}e^{-iqh} +bA^{n}e^{iqh}</math> | |||
Escrito de outra forma: | |||
<math> A^{n+1}\left[1+\frac{i\Delta t}{2} V_j -b(e^{-iqh}-2+e^{iqh})\right] = A^{n}\left[1-\frac{i\Delta t}{2} V_j +b(e^{-iqh}-2+e^{iqh})\right] </math> | |||
Utilizando relações trigonométricas: | |||
<math> A^{n+1}\left[1+\frac{i\Delta t}{2} V_j -b(-sin^2(\frac{qh}2))\right] = A^{n}\left[1-\frac{i\Delta t}{2} V_j +b(-sin^2(\frac{qh}2))\right]</math> | |||
Assim, obtemos o fator de amplificação: | |||
<math>\left|\frac{A^{n+1}}{A^n}\right| = \left|\frac{1-\frac{i\Delta t}{2} V_j -b(sin^2(\frac{qh}2))}{1+\frac{i\Delta t}{2} V_j +b(sin^2(\frac{qh}2))}\right| \leq 1</math> | |||
Portanto, o método é incondicionalmente estável. | |||
== Exemplos de Potenciais == | |||
=== Oscilador Harmônico === | |||
O oscilador harmônico quântico consiste de uma partícula em uma zona onde o potencial possui comportamento harmônico, ou seja, depende de <math> x^2 </math>. Em nosso exemplo, inserimos um pacote de formato gaussiano no interior de um potencial harmônico e observamos sua evolução temporal. | |||
[[Arquivo:H_oscilator.gif]] | |||
Abaixo encontra-se o código usado em Júlia. | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
# Definição de constantes | |||
ħ = 1 | |||
xmax = 100 | |||
tmax = 150 | |||
m = 1 | |||
Δt = 0.2 | |||
Δx = 0.25 | |||
σ = 2 | |||
k = 75 | |||
ω = 0.1 | |||
x0 = xmax/2 | |||
# Definição do espaço de integração e do pacote de onda inicial | |||
x = collect(0:Δx:xmax) | |||
Ψ_HO = zeros(Complex{Float64}, length(x)) | |||
for (i, val) in enumerate(x) | |||
Ψ_HO[i] = 0.5*exp(-(val - xmax/3)^2/(2*σ^2))*exp(im*k*(val-xmax/3)) | |||
end | |||
# Potencial do oscilador harmônico | |||
function V_HO(x) | |||
return 0.5 * m * (ω^2) * ((x - x0)^2) | |||
end | |||
# Pré-cálculo do potencial do oscilador harmônico | |||
V_HO_values = [V_HO(x_i) for x_i in x[2:end-1]] | |||
# Matrizes de evolução temporal | |||
A_HO = zeros(Complex{Float64}, length(x)-2, length(x)-2) | |||
for i in 1:length(x)-2, j in 1:length(x)-2 | |||
if i == j | |||
A_HO[i, j] = 1 + im * (Δt / (2ħ)) * (ħ^2 / (m * Δx^2) + V_HO_values[i]) | |||
elseif i == j + 1 || i == j - 1 | |||
A_HO[i, j] = -im * (ħ * Δt) / (4 * m * Δx^2) | |||
end | |||
end | |||
invA_HO = inv(A_HO) | |||
B_HO = conj(A_HO) | |||
# Criação do GIF | |||
anim = @animate for t in 0:Δt:tmax | |||
Ψ_HO[2:end-1] .= invA_HO * (B_HO * Ψ_HO[2:end-1]) | |||
plot(x, abs2.(Ψ_HO), xlabel="Position", title="Time: $t", ylims=(0, 1), label="|Ψ|²") | |||
plot!(x, V_HO.(x), label="Potential V(x)") | |||
end | |||
gif_path = "/gif/path/harmonic_oscilator.gif" | |||
gif(anim, gif_path, fps=45) | |||
</source><br /> | |||
=== Barreira (Tunelamento) === | |||
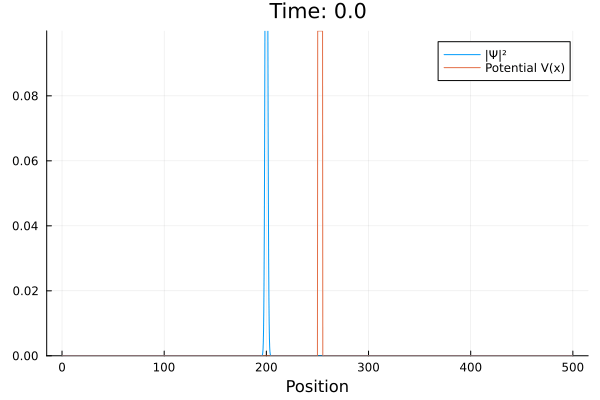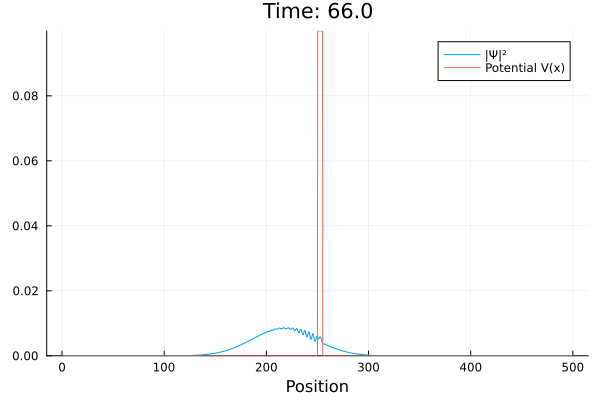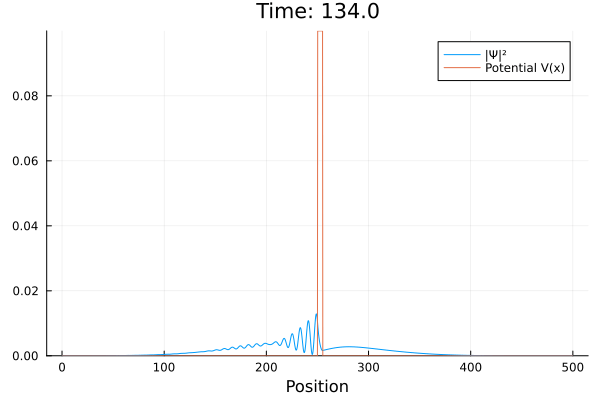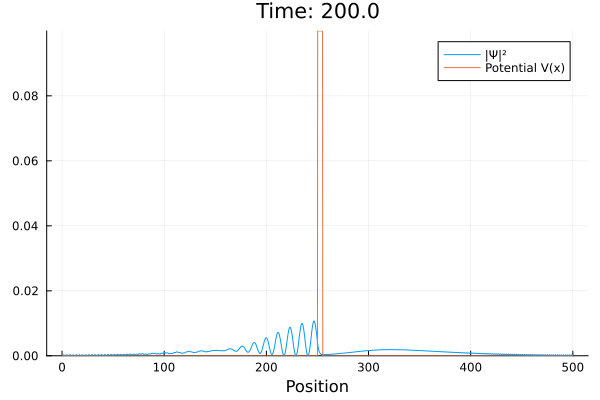
Na mecânica quântica partículas podem existir, mesmo que com baixa probabilidade, em regiões que classicamente seriam proibidas. Este é o caso da barreira, onde uma partícula atravessa uma região onde sua energia total é negativa. Chamamos este fenômeno de tunelamento. A seguir, há um exemplo onde inserimos um pacote de formato gaussiano se deslocando em direção a uma barreira de potencial, de forma que parte da onda é refletida de volta e outra tunela pela barreira. | |||
[[Arquivo:Tunneling.gif]] | |||
Abaixo encontra-se o código usado em Júlia. | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
# Definição de constantes | |||
ħ = 1 | |||
xmax = 500 | |||
tmax = 200 | |||
m = 1 | |||
Δt = 0.2 | |||
Δx = 0.25 | |||
σ = 1.5 | |||
k = 50 | |||
ω = 0.1 | |||
# Definição do espaço de integração e do pacote de onda inicial | |||
x = collect(0:Δx:xmax) | |||
Ψ = zeros(Complex{Float64}, length(x)) | |||
for (i, val) in enumerate(x) | |||
Ψ[i] = Ψ[i] = 0.5*exp(-(val - xmax/2.5)^2/(2*σ^2))*exp(-im*k*(val)) | |||
end | |||
# Potencial barreira | |||
function V(arg) | |||
if arg > xmax*0.5 && arg <= xmax*0.51 | |||
return 0.1 | |||
else | |||
return 0 | |||
end | |||
end | |||
# Pré-cálculo do potencial V | |||
V_values = [V(x_i) for x_i in x[2:end-1]] | |||
# Matrizes de evolução temporal A | |||
A = zeros(Complex{Float64}, length(x)-2, length(x)-2) | |||
for i in 1:length(x)-2, j in 1:length(x)-2 | |||
if i == j | |||
A[i, j] = 1 + im * (Δt / (2ħ)) * (ħ^2 / (m * Δx^2) + V_values[i]) | |||
elseif i == j + 1 || i == j - 1 | |||
A[i, j] = -im * (ħ * Δt) / (4 * m * Δx^2) | |||
end | |||
end | |||
invA = inv(A) | |||
B = conj(A) | |||
# Criação do GIF | |||
anim = @animate for t in 0:Δt:tmax | |||
global Ψ[2:length(x)-1] = invA * (B * Ψ[2:length(x)-1]) | |||
plot(x, abs2.(Ψ), xlabel="Position", title="Time: $t", ylims=(0, 0.1), label="|Ψ|²") | |||
plot!(x, V.(x), label="Potential V(x)") | |||
end every 10 | |||
gif_path = "/gif/path/tunneling.gif" | |||
gif(anim, gif_path, fps = 30) | |||
</source><br /> | |||
=== Poço Finito === | |||
O contrário da barreira é o chamado de poço de potencial. Ao invés da partícula atravessá-lo por completo, uma parte do pacote de onda é refletido, uma parte é transmitido e outra ainda fica preso no meio do poço. Veja o exemplo. | |||
[[Arquivo:Pit.gif]] | |||
Abaixo encontra-se o código usado em Júlia. | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
dt = 0.1 | |||
dx = 0.25 | |||
L = 50 | |||
x = collect(0:dx:L) | |||
size(x) | |||
function V_p(x) | |||
if x<L/3 | |||
return 0.1 | |||
elseif x>2L/3 | |||
return 0.1 | |||
else | |||
return 0 | |||
end | |||
end | |||
b = dt*im/(4*dx^2) | |||
A_p = [if i==j; 1 - 2b - V_p(i)*dt*im/2 elseif i==dx+j || i==j-dx; b else 0 end for i=0:dx:L, j=0:dx:L] | |||
B_p = @. conj(A_p) | |||
IB_p = inv(B_p) | |||
len = length(x) | |||
ψ = [(sqrt(1/(8*pi))*exp(-(val - L/4)^2/(8))*exp(-im*75*(val-L/4))) for val in x] | |||
for (i,num) in enumerate(ψ) | |||
if abs(num)<1e-10; | |||
ψ[i]=0 | |||
end | |||
end | |||
ves_p = @. V_p(x) | |||
t=0 | |||
@gif for t in 0:dt:50 | |||
ψ[2:end-1] = IB_p[2:end-1,2:end-1]*A_p[2:end-1,2:end-1]*ψ[2:end-1] | |||
for (i,num) in enumerate(ψ) | |||
if abs(num)<1e-10; | |||
ψ[i]=0 | |||
end | |||
end | |||
plot(x,abs2.(ψ),c="red",label="|ψ|^2") | |||
#plot!([x for x=0:dx:L],imag(ψ),c="blue") | |||
plot!([x for x=0:dx:L],ves_p,c="blue",label="V(x)") | |||
plot!(ylim=[0,0.15],title="t=$t") | |||
end | |||
</source><br /> | |||
== Referências == | |||
# Griffiths, DAVID. Introduction to Quantum Mechanics 3ed. 2018. | |||
# Scherer, CLÁUDIO. Métodos Computacionais da Física. 2010. | |||
Edição atual tal como às 17h25min de 27 de abril de 2024
Conhecer o estado de uma partícula, na Mecânica Clássica, é saber, em um determinado momento, sua velocidade e sua posição. A partir destes valores, é possível determinar os seus futuros estados utilizando as relações fornecidas pelas Leis de Newton. Na Mecânica Quântica, porém, o estado físico não é mais caracterizado por uma quantidade discreta de valores numéricos, e sim, por uma função. A chamada Função de Onda, , nos informa a evolução temporal do estado quântico de uma partícula, seguindo a Equação de Schrödinger. Em uma dimensão, a Equação de Schrödinger é dada por:
O Método De Crank-Nicolson
A fim de resolvê-la numericamente para diferentes tipos de potenciais, usou-se o Método de Crank-Nicolson de resolução de EDPs. Este método baseia-se em combinar os métodos explícito e implícito (com igual contribuição) para aumentar sua estabilidade.
O método explícito FTCS (Forward Time Central Space) consiste em tomar derivadas temporais "para frente" e manter a derivada espacial centrada.
;
Tomando (unidades atômicas), ao inserirmos as expressões acima na Equação de Schrödinger, temos que:
Simplificando a notação para , onde representa a posição e o tempo, e reorganizando os termos, ficamos com:
O método implícito é semelhante, porém a derivada temporal é "para trás".
O que nos leva a ter:
que, com uma substituição de variável (que é muda), nos dá, enfim:
Como dito, o Método de Crank-Nicolson é uma combinação dos métodos implícito e explícito, cada um tendo o mesmo peso de 1/2. Ao somarmos as duas equações (cada uma multiplicada por 0.5), ficaremos com a seguinte expressão:
que, ao reorganizarmos para isolar os , resulta em:
Para resolver a equação em simultaneamente para ambos os tempos e em todos os pontos, escrevemos a equação em forma matricial:
com .
Podemos notar que a diferença entre as matrizes que multiplicam e é somente o sinal das componente imaginárias. Assim, a equação final pode ser escrita como:
, onde A é a matriz
Estabilidade do Método de Crank-Nicolson
Para verificar a estabilidade, devemos primeiro olhar para a equação que define o método:
Para simplificar, chamaremos de b. Nesse caso, temos:
Definimos os Modos de Fourier:
Assim, obtemos:
Dividindo tudo por :
Escrito de outra forma:
Utilizando relações trigonométricas:
Assim, obtemos o fator de amplificação:
Portanto, o método é incondicionalmente estável.
Exemplos de Potenciais
Oscilador Harmônico
O oscilador harmônico quântico consiste de uma partícula em uma zona onde o potencial possui comportamento harmônico, ou seja, depende de . Em nosso exemplo, inserimos um pacote de formato gaussiano no interior de um potencial harmônico e observamos sua evolução temporal.
Abaixo encontra-se o código usado em Júlia.
using Plots
# Definição de constantes
ħ = 1
xmax = 100
tmax = 150
m = 1
Δt = 0.2
Δx = 0.25
σ = 2
k = 75
ω = 0.1
x0 = xmax/2
# Definição do espaço de integração e do pacote de onda inicial
x = collect(0:Δx:xmax)
Ψ_HO = zeros(Complex{Float64}, length(x))
for (i, val) in enumerate(x)
Ψ_HO[i] = 0.5*exp(-(val - xmax/3)^2/(2*σ^2))*exp(im*k*(val-xmax/3))
end
# Potencial do oscilador harmônico
function V_HO(x)
return 0.5 * m * (ω^2) * ((x - x0)^2)
end
# Pré-cálculo do potencial do oscilador harmônico
V_HO_values = [V_HO(x_i) for x_i in x[2:end-1]]
# Matrizes de evolução temporal
A_HO = zeros(Complex{Float64}, length(x)-2, length(x)-2)
for i in 1:length(x)-2, j in 1:length(x)-2
if i == j
A_HO[i, j] = 1 + im * (Δt / (2ħ)) * (ħ^2 / (m * Δx^2) + V_HO_values[i])
elseif i == j + 1 || i == j - 1
A_HO[i, j] = -im * (ħ * Δt) / (4 * m * Δx^2)
end
end
invA_HO = inv(A_HO)
B_HO = conj(A_HO)
# Criação do GIF
anim = @animate for t in 0:Δt:tmax
Ψ_HO[2:end-1] .= invA_HO * (B_HO * Ψ_HO[2:end-1])
plot(x, abs2.(Ψ_HO), xlabel="Position", title="Time: $t", ylims=(0, 1), label="|Ψ|²")
plot!(x, V_HO.(x), label="Potential V(x)")
end
gif_path = "/gif/path/harmonic_oscilator.gif"
gif(anim, gif_path, fps=45)
Barreira (Tunelamento)
Na mecânica quântica partículas podem existir, mesmo que com baixa probabilidade, em regiões que classicamente seriam proibidas. Este é o caso da barreira, onde uma partícula atravessa uma região onde sua energia total é negativa. Chamamos este fenômeno de tunelamento. A seguir, há um exemplo onde inserimos um pacote de formato gaussiano se deslocando em direção a uma barreira de potencial, de forma que parte da onda é refletida de volta e outra tunela pela barreira.
Abaixo encontra-se o código usado em Júlia.
using Plots
# Definição de constantes
ħ = 1
xmax = 500
tmax = 200
m = 1
Δt = 0.2
Δx = 0.25
σ = 1.5
k = 50
ω = 0.1
# Definição do espaço de integração e do pacote de onda inicial
x = collect(0:Δx:xmax)
Ψ = zeros(Complex{Float64}, length(x))
for (i, val) in enumerate(x)
Ψ[i] = Ψ[i] = 0.5*exp(-(val - xmax/2.5)^2/(2*σ^2))*exp(-im*k*(val))
end
# Potencial barreira
function V(arg)
if arg > xmax*0.5 && arg <= xmax*0.51
return 0.1
else
return 0
end
end
# Pré-cálculo do potencial V
V_values = [V(x_i) for x_i in x[2:end-1]]
# Matrizes de evolução temporal A
A = zeros(Complex{Float64}, length(x)-2, length(x)-2)
for i in 1:length(x)-2, j in 1:length(x)-2
if i == j
A[i, j] = 1 + im * (Δt / (2ħ)) * (ħ^2 / (m * Δx^2) + V_values[i])
elseif i == j + 1 || i == j - 1
A[i, j] = -im * (ħ * Δt) / (4 * m * Δx^2)
end
end
invA = inv(A)
B = conj(A)
# Criação do GIF
anim = @animate for t in 0:Δt:tmax
global Ψ[2:length(x)-1] = invA * (B * Ψ[2:length(x)-1])
plot(x, abs2.(Ψ), xlabel="Position", title="Time: $t", ylims=(0, 0.1), label="|Ψ|²")
plot!(x, V.(x), label="Potential V(x)")
end every 10
gif_path = "/gif/path/tunneling.gif"
gif(anim, gif_path, fps = 30)
Poço Finito
O contrário da barreira é o chamado de poço de potencial. Ao invés da partícula atravessá-lo por completo, uma parte do pacote de onda é refletido, uma parte é transmitido e outra ainda fica preso no meio do poço. Veja o exemplo.
Abaixo encontra-se o código usado em Júlia.
using Plots
dt = 0.1
dx = 0.25
L = 50
x = collect(0:dx:L)
size(x)
function V_p(x)
if x<L/3
return 0.1
elseif x>2L/3
return 0.1
else
return 0
end
end
b = dt*im/(4*dx^2)
A_p = [if i==j; 1 - 2b - V_p(i)*dt*im/2 elseif i==dx+j || i==j-dx; b else 0 end for i=0:dx:L, j=0:dx:L]
B_p = @. conj(A_p)
IB_p = inv(B_p)
len = length(x)
ψ = [(sqrt(1/(8*pi))*exp(-(val - L/4)^2/(8))*exp(-im*75*(val-L/4))) for val in x]
for (i,num) in enumerate(ψ)
if abs(num)<1e-10;
ψ[i]=0
end
end
ves_p = @. V_p(x)
t=0
@gif for t in 0:dt:50
ψ[2:end-1] = IB_p[2:end-1,2:end-1]*A_p[2:end-1,2:end-1]*ψ[2:end-1]
for (i,num) in enumerate(ψ)
if abs(num)<1e-10;
ψ[i]=0
end
end
plot(x,abs2.(ψ),c="red",label="|ψ|^2")
#plot!([x for x=0:dx:L],imag(ψ),c="blue")
plot!([x for x=0:dx:L],ves_p,c="blue",label="V(x)")
plot!(ylim=[0,0.15],title="t=$t")
end
Referências
- Griffiths, DAVID. Introduction to Quantum Mechanics 3ed. 2018.
- Scherer, CLÁUDIO. Métodos Computacionais da Física. 2010.




























![{\displaystyle A^{n+1}\left[1+{\frac {i\Delta t}{2}}V_{j}-b(e^{-iqh}-2+e^{iqh})\right]=A^{n}\left[1-{\frac {i\Delta t}{2}}V_{j}+b(e^{-iqh}-2+e^{iqh})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3d2a2f83a223c0e2824e622ce444293a176381)
![{\displaystyle A^{n+1}\left[1+{\frac {i\Delta t}{2}}V_{j}-b(-sin^{2}({\frac {qh}{2}}))\right]=A^{n}\left[1-{\frac {i\Delta t}{2}}V_{j}+b(-sin^{2}({\frac {qh}{2}}))\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ee0bc2c7172a2d31feeea37073f80f216c67ca)