Grupo - Correlações no Movimento de Átomos em Argônio
Aluno: Edelson Luis Pinheiro Sezerotto Júnior (288739) - Engenharia Física
Introdução
Ao realizar uma simulação de Dinâmica Molecular, frequentemente estamos interessados em quantificar as relações que existem entre os movimentos das partículas do sistema. Por que isso é útil? Bem, geralmente, o programa trabalha com informações como: velocidades e posições de cada uma das partículas, energia total e temperatura do sistema etc. Mas podemos querer obter informações tais como: qual o estado físico em que o sistema se encontra? As partículas estão se movendo de forma restrita ou elas conseguem se difundir bastante ao longo do sistema? O quanto as condições iniciais influenciam a evolução temporal do sistema? Para responder perguntas como essas - e outras - serão introduzidas aqui três das principais formas de medir correlações entre as partículas - isto é, maneiras de obter uma visão geral do sistema em estudo: função de distribuição radial, deslocamento quadrado médio e função de autocorrelação de velocidades.
Um algoritmo para Dinâmica Molecular
Um dos objetivos desse texto é sugerir algoritmos para implementar os cálculos de correlação apresentados. Para isso, coloco abaixo um algoritmo de Dinâmica Molecular considerando que a interação entre as partículas é do tipo Lennard-Jones (e portanto os átomos são de argônio) - ou seja, a força que uma exerce sobre a outra é dada por
O algoritmo é como segue:
N é o número de partículas, L é a largura do sistema (quadrado), dt é o intervalo de tempo que decorre a cada iteração, t é o tempo inicial, tmax é o tempo final, e são as posições iniciais e e são as velocidades iniciais.
Os outros algoritmos apresentados ao longo desse texto devem ser utilizados em conjunto com o algoritmo acima.
Função de Distribuição Radial (RDF)
A RDF (do inglês Radial Distribution Function) é uma função que descreve o quanto, em média, as partículas de um sistema estão radialmente compactadas, sendo uma forma muito efetiva de descrever a estrutura de sistemas moleculares desordenados, como líquidos.
A RDF pode ser obtida experimentalmente a partir de, por exemplo, difração de nêutrons. Comparar os resultados numéricos com os experimentais é portanto uma ótima forma de descobrir se as simulações estão seguindo uma base teórica correta (e caso não estejam, seus resultados podem sugerir maneiras de melhorar a teoria usada para descrever a interação entre as partículas).
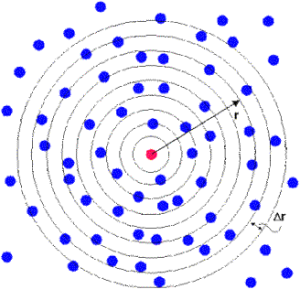
Para determinar a RDF deve-se primeiro escolher uma partícula do sistema (partícula de origem) e imaginar que ao redor dela são desenhadas um conjunto de esferas concêntricas a uma pequena distância umas das outras, conforme a figura abaixo (pode-se dizer que temos cascas esféricas de espessura ):
A ideia da função é a seguinte: a cada iteração, armazenam-se os valores referentes às quantidades de partículas dentro de cada casca. Define-se então a quantidade , que é a quantidade média de partículas por casca dentro de um raio a partir da partícula de origem. Usando também a densidade de partículas ao longo de todo o sistema, , define-se a RDF pela relação abaixo:
Analisando a equação para com cuidado, identificamos o termo como sendo a quantidade média de partículas em cada casca considerando o sistema como um todo.
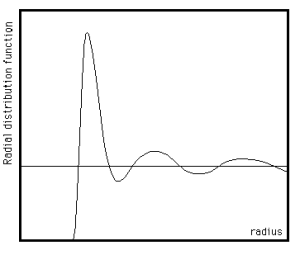
Se for grande o bastante, também será "a quantidade média de partículas em cada casca considerando o sistema como um todo" (reflita sobre por que isso é verdade), e esperamos que se aproxime de 1. Assim, um gráfico típico para é como na figura abaixo:
Existem algumas coisas importantes a se notar no gráfico: primeiramente, para distâncias muito curtas, é nulo. Isso é esperado porque nas vizinhanças de uma partícula não existem outras partículas (se não fosse assim, haveriam partículas separadas por uma distância infinitesimal ou nula). Os picos ocorrem porque, havendo uma certa ordenação na estrutura do material (que existe no caso do argônio líquido), haverá regiões de maior concentração atômica. Quanto menor a temperatura, mais pronunciados serão os picos. Por fim, nota-se que para grandes distâncias, realmente tende a 1, como já era esperado.
Algoritmo
Deslocamento Quadrado Médio (MSD)
O MSD (do inglês Mean Square Displacement) é uma medida de quanto as partículas estão difundindo. Devemos lembrar do seguinte: se as moléculas de líquido (ou de um gás, ou de outro sistema de partículas com certa liberdade de movimento) estão confinadas em uma região do espaço sendo que existe outra região vazia para a qual elas podem migrar, elas o farão através do processo de difusão.
Analisando o movimento individual de uma certa partícula em uma simulação, percebemos que tal movimento é bastante complexo: ela é continuamente jogada para direções diferentes conforme interage com as outras partículas. O caminho feito por ela pode então ser aproximado por uma caminhada aleatória. Esse é um tipo de movimento idealizado no qual uma partícula, a cada passagem temporal, move-se em uma certa direção de maneira aleatória.
Se fôssemos analisar a distância média percorrida pelas partículas como função do tempo, teríamos o problema de que ela seria aproximadamente 0 (por ser aleatória) e portanto não seria uma medida útil. Podemos, alternativamente, analisar a média dos quadrados dos deslocamentos ao longo do tempo, porque esse certamente será um valor não nulo. Foi demonstrado por Einstein que tal valor, , possui uma dependência linear do tempo, conforme a equação
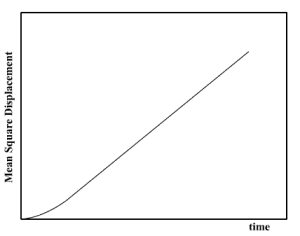
O termo é chamado de coeficiente de difusão e é uma medida da taxa com a qual as partículas se difundem - um grande valor de implica que pequenas passagens de tempo acarretam em grandes deslocamentos para as partículas, o que indica que elas estão se difundindo rapidamente. Qual a utilidade de saber se elas estão se difundindo? Um dos principais motivos é que isso fornece uma pista do estado físico em que se encontra o material: sólidos terão valores menores de do que líquidos, que por sua vez terão valores menores do que os gases. Além, disso, fornece uma ideia da estrutura do sistema em estudo: um cristal, por exemplo, deve possuir um valor de quase nulo porque os átomos realizam apenas pequenos deslocamentos em torno de uma posição de equilíbrio bem delimitada. Uma curva típica para o MSD em função do tempo é como mostrado abaixo:
Deve-se notar que o comportamento linear não se observa para intervalos de tempo muito pequenos porque as partículas não tem seu movimento muito afetado e a força sobre elas é aproximadamente constante, o que gera um movimento uniformemente variado e portanto um deslocamento ao longo do tempo aproximadamente parabólico.
Algoritmo
Função de Autocorrelação de Velocidades (VAF)
A VAF (do inglês Velocity Autocorrelation Function) é uma função que relaciona as velocidades das partículas em um instante inicial com as próprias velocidades, em um instante final - daí o termo autocorrelação. Isso serve para revelar o quão dependente das condições iniciais é a evolução do sistema.
A VAF é calculada como se segue: escolhemos um tempo inicial e armazenamos os componentes (que no caso bidimensional são 2) das velocidades de todas as partículas em uma lista . Essa lista então contém velocidades , onde é o índice de uma dada partícula; e são os componentes da velocidade no instante .
Criamos então uma lista , onde seu primeiro item será dado por:
Após decorrer um intervalo de tempo , podemos calcular um novo item para dado por:
ou seja, a média dos produtos escalares entre as velocidades das partículas no tempo e em
Podemos repetir esse procedimento para cada passo temporal e ir obtendo novos itens para , de acordo com a fórmula geral abaixo:
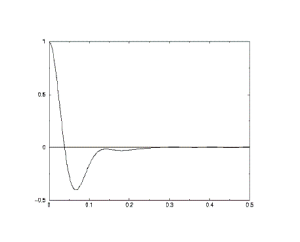
Tendo calculado vários valores de , podemos plotar seu gráfico, que, para líquidos, costuma ser parecido com a figura abaixo (normalizada - isto é, reescalada para que seu máximo seja 1):
Vamos agora analisar como a VAF pode ser útil. Digamos que os átomos não interagissem entre si. Suas velocidades então não mudariam e seria constante, com um gráfico consistindo de uma linha horizontal. Assim, um gráfico quase horizontal indica forças intermoleculares muito fracas.
Além disso, o formato do gráfico permite outras conclusões interessantes. O gráfico começa com um valor grande e positivo, indicando que no começo as velocidades evoluem de forma bastante dependente das velocidades iniciais. Isso é verdade porque pouco depois de , as velocidades ainda estão apontando para direções muito próximas das iniciais, tornando o somatório de produtos escalares um valor grande e positivo. Com o passar do tempo, as partículas vão colidindo e as velocidades passam a ter componentes negativos. Isso gera termos negativos no cálculo de , que começa a diminuir até se tornar negativo (gerando o vale visto no gráfico).
Por fim, o VAF dá mais uma pista do estado físico do sistema. Por exemplo, em sólidos ordenados, as partículas ficam oscilando em torno de suas posições de equilíbrio, com as velocidades alternando suas direções e fazendo com que o gráfico apresente oscilações; nos líquidos, as partículas começam a se difundir e isso impede um movimento oscilatório. A difusão faz com que elas se afastem e isso diminui a interação entre elas. Agora elas tem velocidades aleatórias e pouca interação, fazendo tender a 0.
Algoritmo
Referências
A. Rahman (1964). "Correlations in the Motion of Atoms in Liquid Argon". Physical Review
Democritus [1]



































![{\displaystyle >>>~~~~msd={\frac {\sum [(x_{i}-x_{i0})^{2}+(y_{i}-y_{i0})^{2}]}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1118adff1a25826a7d9a2c7d6ffca95f2d810e6b)