Grupo1 - Dif em 2D

A equação de Poisson:

$\Delta u={\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=-g(x,y)$

é uma equação do tipo Elíptica que representa fenômenos físicos estácionarios relacionados a Eletrostatica, Dinâmica de Fluídos e Transferência de Calor. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,y) \equiv 0 } a equação passa a ser chamada de Equação de Laplace. Os problemas relacionados a equação de Laplace são estudados pela "Teoria do Potencial".

As soluções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = u(x,y) } da Equação de Laplace são denominadas funções Harmônicas. Os problemas mais habituais na vida de um físico, engenheiro ou matemático ao se depararem com uma EDP, são os problemas com Condições de Contorno em um dominío Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \in \mathbb{R}^2} , essencialmente será trabalhada a Condição de Dirichlet, que possui fronteiras (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial \Omega } ) conhecidas, tendo o seguinte formato:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = 0 & \text{para } (x,y) \in \Omega, \\ u = f(x,y) & \text{para } (x,y) \in \partial \Omega. \end{cases} }

A equação de Poisson possui forma parecida para o Problema de Dirichlet, que fica:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = - g(x) & \text{para } (x,y) \in \Omega, \\ u = f(x,y) & \text{para } (x,y) \in \partial \Omega. \end{cases} }

Para tais problemas, estudaremos os métodos de Relaxação e Super-Relaxação para encontrar as soluções da Equação de Laplace na região de Quadrado de Lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \{ \Omega = (0,L)\times (0,L) \} ) } .

Dominio Quadrado de Lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L }

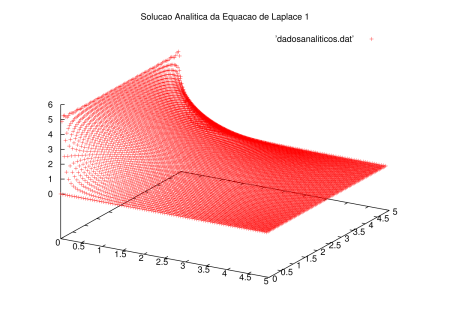
Solução Analítica da Equação de Laplace

Seja o problema em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0, L) \times (0, L)} , temos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u(x,y) = 0 \text{ em } \Omega \\ u(x, y) = f(x) \text{ em } \partial \Omega \end{cases} }

sendo

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \begin{cases} f(0,y) = f_{1}(y); \\ f(L,y) = f_{2}(y); \\ f(x,0) = f_{3}(x); \\ f(x,L) = f_{4}(x). \end{cases} }

Separamos o problema geral de Dirchlet em 4 problemas "menores", com condições de contorno diferentes de zero em apenas um trecho da fronteira, de modo que obtemos desde:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u_{1}(x,y) = 0 \text{ em } \Omega; \\ u_{1}(0,y) = f_{1}(y) \text{ para } y \in (0, L); \\ u_{1}(L,y) = u_{1}(x,0) = u_{1}(x,L) =0, \end{cases} }

...

até:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u_{4}(x,y) = 0 \text{ em } \Omega; \\ u_{4}(x,L) = f_{4}(x) \text{ para } x \in (0, L); \\ u_{4}(0,y) = u_{4}(L,y) = u_{4}(x,0) =0. \end{cases} }

Podemos então utilizar o Método da Separação de Variáveis para resolver os 4 problemas e, como a Equação de Laplace é linear, sua soma será a solução completa do Problema de Dirichlet. O método consiste em supor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x, y) = \phi(x)\theta(y)} , para então, ao substituirmos na equação obtermos a seguinte expressão:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta u_{i} = \ddot{\phi_{i}}(x)\theta_{i}(y) + \phi_{i}(x) \ddot{\theta_{i}}(y) = 0 }

Podemos isolar as funções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{i}} , de fato ficamos com com duas relações que dependem ou apenas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } portanto para elas serem sempre iguais, é necessário que sejam constantes (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \lambda} ):

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\ddot{\phi_{i}}}{\phi_{i}} = -\frac{\ddot{\theta_{i}}}{\theta_{i}} = \lambda }

Assim obtemos 2 EDOs de segunda ordem, que podem ser resolvidas pelo Método dos Coeficientes a Determinar. Como não é objetivo aqui realizar cálculos analíticos (especialmente "na mão") apenas será resolvido o primeiro problema (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}(x, y)} ):

As condições de contorno mostram que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(L)\theta(y) = 0 \Rightarrow \phi(L) = 0 } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(x)\theta(0) = 0 \Rightarrow \theta(0) = 0 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(x)\theta(L) = 0 \Rightarrow \theta(L) = 0 } .

Dividindo o problema, temos a parte de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \ddot{\phi_{1}}(y) - \lambda \phi_{1} =0; \\ \phi_{1} (L) = 0; \\ \end{cases} }

Supondo uma solução da forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1}(x) = Ae^{sx}} :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{\phi_{1}} - \lambda \phi_{1} = s^{2}Ae^{sx} - \lambda Ae^{sx} = 0 \Longrightarrow} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = \pm \sqrt{\lambda} }

Ou seja, temos a solução de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1}} sendo

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1}(x) = A_{1}e^{\sqrt{\lambda} x} + A_{2}e^{- \sqrt{\lambda} x} }

Partindo para a segunda equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{1}(y) } ,

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \ddot{\theta_{1}}(x) + \lambda \theta_{1} =0; \\ \theta_{1} (0) = 0 \\ \theta_{1} (L) = 0; \end{cases} }

supondo solução do tipo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{1} (y) = Be^{i\omega y} } temos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{\theta_{1}} + \theta_{1} = -\omega^2 Be^{i\omega y} + \lambda Be^{i\omega y} = 0 \Longrightarrow } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \pm \sqrt{\lambda} }

Ou seja, temos solução Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{1}(y) = B_{1}e^{i\sqrt{\lambda} y} + B_{2}e^{-i\sqrt{\lambda} y} }

Utilizando a primeira C.C. obtemos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{1} = - B_{2} = B}

ou seja, temos que

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{1}(y) = B sen(\sqrt{\lambda} y ). } Utilizando a segunda C.C. temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 = sen(\sqrt{\lambda} y) \Rightarrow \lambda = \frac{n^2 \pi^2}{L^2}, }

ou seja, existem infinitos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} tal que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{1}} é solução.

Voltando a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1}} , temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1}(x) = senh(\frac{n\pi (L-x)}{L}). }

Finalmente unindo as respostas, temos

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{1}(x, y) = \phi_{1}(x) \theta_{1}(y) = \sum C_{1n} \frac{senh(\frac{n \pi(L- x)}{L})}{senh(n\pi)}sen(\frac{n \pi y}{L})}

sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{1n} = \frac{2}{L}\int_{0}^{L} f_{1}(y) sen(\frac{n \pi y}{L}) dy}

Para os outros problemas, temos soluções parecidas:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{2}(x, y) = \phi_{2}(x) \theta_{2}(y) = \sum C_{2n} \frac{senh(\frac{n \pi x}{L})}{senh(n\pi)}sen(\frac{n \pi y}{L});} sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{2n} = \frac{2}{L}\int_{0}^{L} f_{2}(x) sen(\frac{n \pi y}{L}) dy,}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{3}(x, y) = \phi_{3}(x) \theta_{3}(y) = \sum C_{3n} \frac{senh(\frac{n \pi(L- y)}{L})}{senh(n\pi)}sen(\frac{n \pi x}{L});} sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{3n} = \frac{2}{L}\int_{0}^{L} f_{3}(y) sen(\frac{n \pi x}{L}) dx,}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{4}(x, y) = \phi_{4}(x) \theta_{4}(y) = \sum C_{4n} \frac{senh(\frac{n \pi y}{L})}{senh(n\pi)}sen(\frac{n \pi x}{L});} sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{4n} = \frac{2}{L}\int_{0}^{L} f_{4}(x) sen(\frac{n \pi x}{L}) dx.}

A solução completa do problema de Dirichlet no quadrado de Lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} é a soma das quatro soluções parciais: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x, y) = u_{1}(x, y) + u_{2}(x, y) + u_{3}(x, y) + u_{4}(x, y) } .

Método da Relaxação

O Método da Relaxação é um método iterativo utilizado para obter a solução numérica para a equação de Laplace e Poisson. A ideia do método é de, utilizando a vizinhança iterar os pontos da malha até que convirjam para uma solução.

Discretizando a equação temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\mapsto x_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y\mapsto y_{j}} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = 1, ..., N} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = \Delta x = \Delta y = N/L} a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x, y) = g_{ij}} , nos deparamos com uma matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{M}_{i j} = u(x_{i},y_{j}) = u_{i j}} quadrada sendo as bordas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{M}_{1 j} = f(0, y) = u_{1 j}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{M}_{N j} = f(L, y) = u_{N j}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{M}_{i 1} = f(x, 0) = u_{i 1}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{M}_{i N} = f(x, L) = u_{i N}} .

Realizando-se a discretização, podemos tomar as derivadas:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial x^2} = \frac{u_{(i+1) j} + u_{(i-1) j} -2u_{i j}}{h^2} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u}{\partial y^2} = \frac{u_{i (j+1)} + u_{i (j-1)} -2u_{i j}}{h^2} }

Substituindo na Equação, temos

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{u_{(i+1) j} + u_{(i-1) j} -2u_{i j}}{h^2} + \frac{u_{i (j+1)} + u_{i (j-1)} -2u_{i j}}{h^2} = - g_{ij} } , ou seja:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i j} = \frac{u_{(i-1) j} + u_{(i+1) j} + u_{i (j-1)} + u_{i (j+1)} + h^{2}g_{ij}}{4}} ,

ou mais geralmente (supondo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x \neq \Delta y} ):

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i j} = \frac{(\Delta y)^{2}(u_{(i-1) j} + u_{(i+1) j}) + (\Delta x)^2(u_{i (j-1)} + u_{i (j+1)}) + (\Delta y \Delta x)^2 g_{ij}}{2((\Delta x)^2 + (\Delta y)^2)}, }

para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j = 2, ..., N+1 }

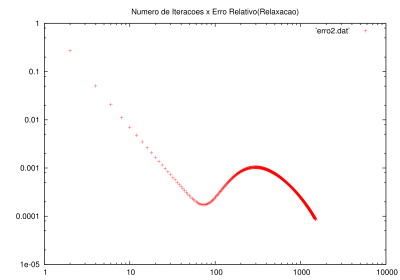
Para condição de parada, foi convencionado tomar o erro relativo entre as iterações Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k+1 } , para estimar o erro, se optou por tomar como valores, o ponto médio da malha (já que é o ultimo ponto a ser alcançado nas iterações, portanto, quando sua variação diminuir é sinal de que a solução já está convergindo), para observarmos a evolução em relação a outros pontos que variam desde o inicio, foram utilizados as diagonais interiores, tal que o erro relativo é:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \Big|\frac{v^{k} - v^{k+1}}{v^{k}}\Big|}

fazendo a média ponderada com peso 4 para o ponto médio:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{k} = \frac{1}{8} (u_{2 2} + u_{2 (N+1)} + u_{(N+1) 2} + 4u_{\frac{(N+2)}{2} \frac{(N+2)}{2}}+u_{(N+1) (N+1)}) }

Método da Super Relaxação (SOR)

Podemos também realizar uma média entre os valores já calculados e os ainda não calculados na iteração, o método da Super Relaxação ou Sobrerrelaxação (SOR) é da seguinte forma:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{ij}^{k+1} = u_{i j}^{k}(1 - \omega) + \omega u_{ij}^{R} }

tal que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{ij}^{R} } é o valor calculado através do método da Relaxação e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \in [0:2]} é o fator de relaxamento, se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = 1 } temos a Relaxação normal.

Estabilidade

Relaxação

Erro relativo (método da Relaxação) em função da quantidade de iterações

A relaxação é um método Iterativo sobre os pontos vizinhos que pode ser feita de 2 modos, pelo Algoritmo de Jacobi, e pelo de Gauss-Seidel.

O algoritmo de Jacobi pega valores "antigos" para a iteração e possui convergencia muito lenta, por isso não é muito utilizado. Já o algoritmo de Gauss-Seidel pega os valores "novos" (que ja foram calculados na iteração) e os "antigos" (que não foram calculados na iteração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } ), possui convergência mais rapida, porém ainda é lenta.

Como a média definida anteriormente foi feita utilizando o ponto médio do domínio, o erro cresce após decair, pois é quando efetivamente ocorrem variações maiores no ponto médio.

Para a relaxação, o algoritmo de Jacobi faz o seguinte cálculo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i j}^{k+1} = \frac{u_{(i-1) j}^{k} + u_{(i+1) j}^{k} + u_{i (j-1)}^{k} + u_{i (j+1)}^{k} + h^{2}g_{ij}}{4}} ,

já o algoritmo de Gauss-Seidel faz:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{i j}^{k+1} = \frac{u_{(i-1) j}^{k+1} + u_{(i+1) j}^{k} + u_{i (j-1)}^{k+1} + u_{i (j+1)}^{k} + h^{2}g_{ij}}{4}} ,

Algoritmos iterativos tendem a convergir para solução unica, se a matriz que as representa for Diagonal Dominante, ou seja:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a_{ii}| \ge \sum_{j=1 (i\neq j)}^{N} |a_{ij}| }

Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{ii} = u_{ii} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{ij} = u_{ij} } , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |u_{ii}| = 4 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |u_{ij}| = 1 } e

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1 (i\neq j)}^{N+2} |a_{ij}| = 4 }

Como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 = 4 } , a desigualdade vale e o método converge.

De fato, podemos ver que a equação de Laplace respeita tal desigualdade.

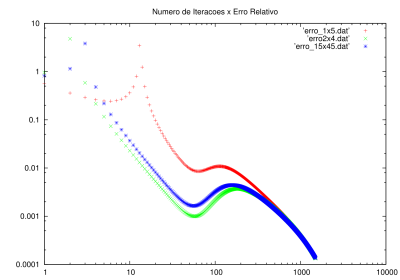
Caso façamos um retangulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{x} \neq L_{y} } com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x \neq \Delta y } , obtemos os erros da imagem a seguir, feito utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{x} =1 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{y} = 5 } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{x} =2 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{y} = 4 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{x} =1.5 } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{y} = 4.5 } :

Super Relaxação

Grafico mostra a quantidades de Iterações para convergência do exemplo 1 em função de omega

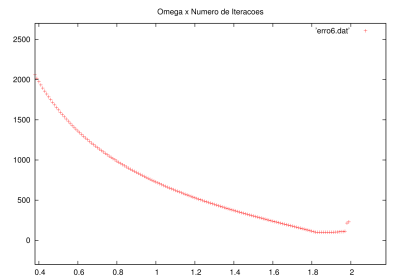
Como o método depende de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega } , e se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = 1 } temos a Relaxação normal, então podemos já observar que a convergência será mais demorada se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega < 1 } , já quando maior que 1, a solução sempre converge mais rápido até um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{otimo} } após o valor ótimo o valor cresce até 2, valor que diverge para o SOR.

Usaremos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \frac{2}{1+sen(\pi \Delta x)} } que é o valor ótimo.

Exemplos

Foram realizados 5 exemplos, 2 sobre a equação de Laplace e 3 sobre a equação de Poisson.

Exemplo 1

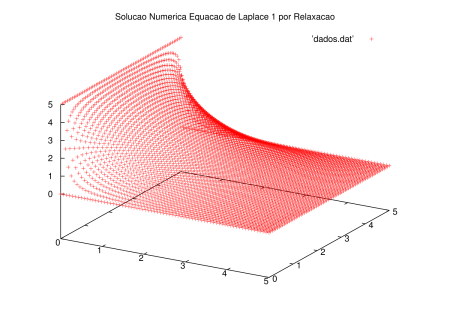
O primeiro problema,que pode ser descrito como a temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = T(x, y)} de uma chapa que está em equilíbrio térmico com um dos lados a temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T(x, 0) = L} , todos os outros lados iguais com temperatura 0 e sem geração. Para o domínio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0;L) \times (0;L) } , tal problema é descrito pela seguinte expressão:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = 0 \forall x,y \in \Omega \\ u(x,0) = L \big( \forall x \in [0;L] \big) \\ u(x, L) = 0 \big( \forall x \in [0;L] \big) \\ u(0, y) = 0 \big( \forall y \in [0;L] \big) \\ u(L, y) = 0 \big( \forall y \in [0;L] \big) . \end{cases} }

A solução analítica para o problema é:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x, y) = \frac{4L}{\pi}\sum_{n=0}^{\infty} \frac{sen(\frac{(2n+1) \pi x}{L})}{2n+1} \frac{senh\Big(\frac{(2n+1) \pi (L-y)}{L}\Big)}{ senh((2n+1)\pi)} }

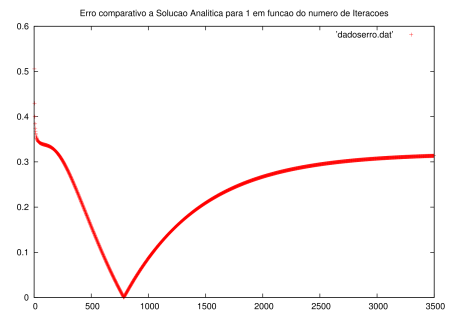
Foi possível obter o gráfico da função analítica aproximada com os 110 primeiros termos parciais e estimar o erro entre a solução numérica e a solução analítica, que foi alto devido ao truncamento da série que forma a solução analítica.

Solução analítica do Problema de Contorno 1

Erro entre solução numérica e solução analítica em função do número de iterações

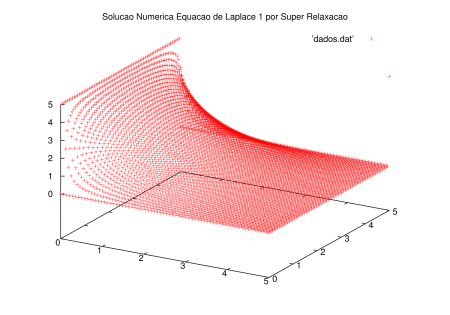
Foram obtidas as soluções mostradas nos gráficos a seguir, através do algoritmo de Gauss-Seidel, no caso da relaxação foram necessárias 1471 iterações para a solução convergir, já SOR levou 1000.

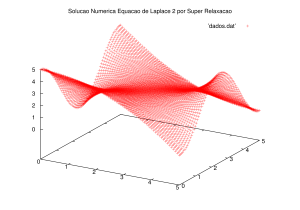
Exemplo 2

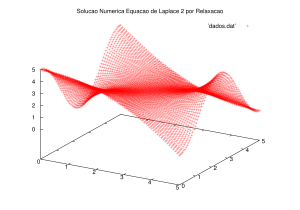
O segundo problema é descrito pela seguinte expressão, para o domínio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0;L) \times (0;L) } :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = 0 \forall x,y \in \Omega \\ u(x,0) = Lsin(\frac{\pi x}{L}) \big( \forall x \in [0;L] \big) \\ u(x, L) = Lcos(\frac{\pi x}{L}) \big( \forall x \in [0;L] \big) \\ u(0, y) = \frac{x^{2}}{L} \big( \forall y \in [0;L] \big) \\ u(L, y) = \frac{(L-x)^{2}}{L} \big( \forall y \in [0;L] \big) . \end{cases} }

Foram obtidas as seguintes soluções mostradas nos gráficos, através do algoritmo de Gauss-Seidel.

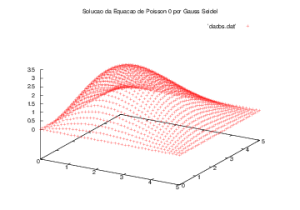
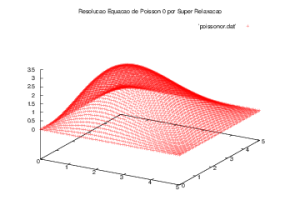
Exemplo 3

O primeiro problema sobre a equação de Poisson , possui contornos fixos e uma gaussiana, pode ser considerado um problema de eletrostática com distribuição de carga Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\rho}{\epsilon_{0}} = xy e^{-(x^2+ y^2)} } . Tal problema é descrito pela seguinte expressão, para o domínio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0;L) \times (0;L) } :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = -g(x, y) = -xye^{-(x^2 + y^2)} \forall x,y \in \Omega \\ u(x,0) = 0 \big( \forall x \in [0;L] \big) \\ u(x, L) = 0 \big( \forall x \in [0;L] \big) \\ u(0, y) = 0 \big( \forall y \in [0;L] \big) \\ u(L, y) = 0 \big( \forall y \in [0;L] \big) . \end{cases} }

Foram obtidas as soluções mostradas nos gráficos a seguir, através do algoritmo de Gauss-Seidel.

Exemplo 4

O segundo problema sobre a equação de Poisson, que é descrito pela seguinte expressão, para o domínio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0;L) \times (0;L) } :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = -g(x, y) = -xye^{-(x^2 + y^2)} \forall x,y \in \Omega \\ u(x,0) = 0 \big( \forall x \in [0;L] \big) \\ u(x, L) = L \big( \forall x \in [0;L] \big) \\ u(0, y) = 0 \big( \forall y \in [0;L] \big) \\ u(L, y) = 0 \big( \forall y \in [0;L] \big) . \end{cases} }

Foram obtidas as soluções mostradas nos gráficos a seguir, através do algoritmo de Gauss-Seidel.

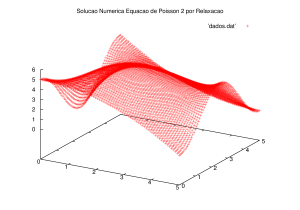
Exemplo 5

O segundo problema sobre a equação de Poisson, que é descrito pela seguinte expressão, para o domínio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = (0;L) \times (0;L) } :

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Delta u = -g(x, y) = -xye^{-(x^2 + y^2)} \forall x,y \in \Omega \\ u(x,0) = Lsin(\frac{\pi x}{L}) \big( \forall x \in [0;L] \big) \\ u(x, L) = Lcos(\frac{\pi x}{L}) \big( \forall x \in [0;L] \big) \\ u(0, y) = \frac{x^{2}}{L} \big( \forall y \in [0;L] \big) \\ u(L, y) = \frac{(L-x)^{2}}{L} \big( \forall y \in [0;L] \big) . \end{cases} }

Foram obtidas as soluções mostradas nos gráficos a seguir, através do algoritmo de Gauss-Seidel.

O programa utilizado para gerar as soluçoes e erros foi o seguir (ou com pequenas alteraçoes):

Programa

Trechos do programa realizado para os exemplos acima.

Programa para o método de Relaxação (Equação de Laplace):

 #include<stdio.h>
 #include<math.h>
 #define N 1000
 #define M 70
 #define P 1
 #define PI 3.141529
 void gaussseidelL(){  
  double u[M+2][M+2];
  double dx=0, dy=0;
  double L=5., parada=0, erro=0.00001, up=0;
  int i=0, j=0, k=1, a=0;
  dx = L/(M+1);
  dy = L/(M+1);
  for(i=1;i<M+1;i++){
    for(j=1;j<M+1;j++){
      u[i][j] = 1.;
    }
  }
  /* Primeira Solução, GaussSeidel1  */
  for(i=0;i<M+1;i++){
    u[0][i] = L;
    u[M+1][i] = 0.0;
    u[i][0] = 0.0;
    u[i][M+1] = 0.0;
  }
  u[0][M+1] = L;
  u[M+1][M+1] = 0.0;
  /* Segunda Solução, GaussSeidel2
  for(i=0;i<M+1;i++){
    u[0][i] = L*pow(cos(i*dx*PI/L),2);
    u[M+1][i] = L*pow(sin(i*dx*PI/L),2);
    u[i][0] = L -  pow(i*dx,2)/L;
    u[i][M+1] = pow(((M+1)-i)*dx,2)/L;
  }
  u[0][M+1] = L;
  u[M+1][M+1] = 0.0;
  */
  do{
    up = (u[1][1] + u[M/2+1][M/2+1] + u[M][M])/3;
    for(i=1;i<M+1;i++){
      for(j=1;j<M+1;j++){
	u[i][j] = (u[i+1][j] + u[i-1][j] + u[i][j+1] + u[i][j-1])/4;
      }
    }
    k++;
    parada = fabs((up-(u[1][1] + u[M/2+1][M/2+1] + u[M][M])/3)/up);
    if(parada < erro && k>N/5){
      a = 1;
    }else{
      a = 0;
    }
  }while(a == 0);
  for(i=0;i<M+2;i++){
    for(j=0;j<M+2;j++){
      printf("%lf %lf %lf \n",i*dx, j*dy, u[i][j]);
    }
  }
  printf("\n\n");
  return;
 }

Segundo trecho para método de Relaxação, Equação de Poisson

#include<stdio.h>
#include<math.h>
#define N 1000
#define M 70
#define P 1
#define PI 3.141529


void gaussseidelP(){
  
  double u[M+2][M+2], F[M+2][M+2];
  double dx=0, dy=0;
  double L=5., parada=0, erro=0.00001, up=0;
  int i=0, j=0, k=1, a=0;

  dx = L/(M+1);
  dy = L/(M+1);
  
  for(i=1;i<M+1;i++){
    for(j=1;j<M+1;j++){
      u[i][j] = 0.;
      F[i][j] = i*dx*j*dy*exp(-(pow(i*dx,2) + pow(j*dy,2))/L);
    }
  }

 /* Solução Zero, Poisson0  */
  for(i=0;i<M+1;i++){
    u[0][i] = 0;
    u[M+1][i] = 0.0;
    u[i][0] = 0.0;
    u[i][M+1] = 0.0;
  }
  u[0][M+1] = 0;
  u[M+1][M+1] = 0.0;

  
  /* Primeira Solução, PoissonGS1 
  for(i=0;i<M+1;i++){
    u[0][i] = L;
    u[M+1][i] = 0.0;
    u[i][0] = 0.0;
    u[i][M+1] = 0.0;
  }
  u[0][M+1] = L;
  u[M+1][M+1] = 0.0;
  */
  
  
  /* Segunda Solução, PoissonGS2 
  for(i=0;i<M+1;i++){
  u[0][i] = L*pow(cos(i*dx*PI/L),2);
  u[M+1][i] = L*pow(sin(i*dx*PI/L),2);
  u[i][0] = L -  pow(i*dx,2)/L;
  u[i][M+1] = pow(((M+1)-i)*dx,2)/L;
  }
  u[0][M+1] = L;
  u[M+1][M+1] = 0.0;
  */
  
  
  do{    
    up = (u[1][1] + u[M/2+1][M/2+1] + u[M][M])/3;
    
    for(i=1;i<M+1;i++){
      for(j=1;j<M+1;j++){
	u[i][j] = (u[i+1][j] + u[i-1][j] + u[i][j+1] + u[i][j-1] + 4*dx*dx*F[i][j])/4;
      }
    }
    
    k++;
    parada = fabs((up-(u[1][1] + u[M/2+1][M/2+1] + u[M][M])/3)/up);
    if(parada < erro && k>N/5){
      a = 1;
    }else{
      a = 0;
    }
  }while(a == 0);

  for(i=0;i<M+2;i++){
    for(j=0;j<M+2;j++){
      printf("%lf %lf %lf \n",i*dx, j*dy, u[i][j]);
    }
  }

  printf("\n\n");
  return;
}

Trecho de programa que utiliza o método de Super Relaxação para Equação de Laplace:

#include<stdio.h>
#include<math.h>
#define N 1000
#define M 70
#define P 1
#define PI 3.141529


void overrelaxationL(){
  
  double u[M+2][M+2], un[M+2][M+2];
  double dx=0, dy=0, omega=1.;
  double L=5., parada=0, erro=0.00005, up=0;
  int i=0, j=0, k=1, a=0;
  
  omega = 2/(1+PI*dx);

    k = 0;
    
    dx = L/(M+1);
    dy = L/(M+1);
    
    for(i=1;i<M+1;i++){
      for(j=1;j<M+1;j++){
	un[i][j] = 1.;
	u[i][j] = un[i][j];
      }
    }
    /*
    for(i=0;i<M+1;i++){
      un[0][i] = 0.0;
      un[M+1][i] = L;
      un[i][0] = 0.0;
      un[i][M+1] = 0.0;
    }
    un[0][M+1] = 0.0;
    un[M+1][M+1] = L;
    */
    
    for(i=0;i<M+1;i++){
      un[0][i] = L*pow(cos(i*dx*PI/L),2);
      un[M+1][i] = L*pow(sin(i*dx*PI/L),2);
      un[i][0] = L -  pow(i*dx,2)/L;
      un[i][M+1] = pow(((M+1)-i)*dx,2)/L;
    }
    un[0][M+1] = L;
    un[M+1][M+1] = 0.0;   
    
    do{
      
      up = (un[1][1] + 4*un[M/2+1][M/2+1] + un[M][M] + un[1][M] + un[M][1])/8;
      
      for(i=1;i<M+1;i++){
	for(j=1;j<M+1;j++){
	  un[i][j] = (un[i+1][j] + un[i-1][j] + un[i][j+1] + un[i][j-1])/4;
	  u[i][j] = u[i][j]*(1 - omega) + omega*un[i][j];
	  un[i][j] = u[i][j];
	}
      }
      k++;
      parada = fabs((up-(un[1][1] + 4*un[M/2+1][M/2+1] + un[M][M] + un[1][M] + un[M][1])/8)/up);
      if(parada < erro && k>N){
	a = 1;
      }else{
	a = 0;
      }
    }while(a == 0);
    
    for(i=0;i<M+2;i++){
      for(j=0;j<M+2;j++){
	printf("%lf %lf %lf \n",i*dx, j*dy, un[i][j]);
      }
    }

  printf("\n\n");
}

Trecho de programa do algoritmo de Super Relaxação para Equação de Poisson:

#include<stdio.h>
#include<math.h>
#define N 1000
#define M 70
#define P 1
#define PI 3.141529


void overrelaxationP(){
  
  double u[M+2][M+2], un[M+2][M+2], F[M+2][M+2];
  double dx=0, dy=0, omega=1.;
  double L=5., parada=0, erro=0.00005, up=0;
  int i=0, j=0, k=1, a=0;
  
  omega = 2/(1+PI*dx);

    k = 0;
    
    dx = L/(M+1);
    dy = L/(M+1);
    
    for(i=1;i<M+1;i++){
      for(j=1;j<M+1;j++){
	un[i][j] = 1.;
	u[i][j] = un[i][j];
	F[i][j] = i*dx*j*dy*exp(-(pow(i*dx,2) + pow(j*dy,2))/L);
      }
    }

       
    for(i=0;i<M+1;i++){
      un[0][i] = 0.0;
      un[M+1][i] = 0.0;
      un[i][0] = 0.0;
      un[i][M+1] = 0.0;
    }
    un[0][M+1] = 0.0;
    un[M+1][M+1] = 0.0;
    

    /*
    for(i=0;i<M+1;i++){
      un[0][i] = L*pow(cos(i*dx*PI/L),2);
      un[M+1][i] = L*pow(sin(i*dx*PI/L),2);
      un[i][0] = L -  pow(i*dx,2)/L;
      un[i][M+1] = pow(((M+1)-i)*dx,2)/L;
    }
    un[0][M+1] = L;
    un[M+1][M+1] = 0.0;   
    */
    
    do{
      
      up = (un[1][1] + 4*un[M/2+1][M/2+1] + un[M][M] + un[1][M] + un[M][1])/8;
      
      for(i=1;i<M+1;i++){
	for(j=1;j<M+1;j++){
	  un[i][j] = (un[i+1][j] + un[i-1][j] + un[i][j+1] + un[i][j-1] + 4*dx*dx*F[i][j])/4;
	  u[i][j] = u[i][j]*(1 - omega) + omega*un[i][j];
	  un[i][j] = u[i][j];
	}
      }
      k++;
      parada = fabs((up-(un[1][1] + 4*un[M/2+1][M/2+1] + un[M][M] + un[1][M] + un[M][1])/8)/up);
      if(parada < erro && k>N){
	a = 1;
      }else{
	a = 0;
      }
    }while(a == 0);
    
    for(i=0;i<M+2;i++){
      for(j=0;j<M+2;j++){
	printf("%lf %lf %lf \n",i*dx, j*dy, un[i][j]);
      }
    }

  printf("\n\n");
}

Referências

1. [[1]] Biezuner, Rodney Josué,Notas de Aula Métodos Numéricos para Equações Diferenciais Parciais Elípticas (UFMG, 2007)
2. [[2]] Biezuner, Rodney Josué,Introdução às Equações Diferenciais Parciais (UFMG, 2007)
3. Jianping Zhu, Solving Partial Differential Equations on Parallel Computers (World Scientific, 1994)

Grupo: Pedro Barbisan Widniczck