Equação de Fokker-Planck

Grupo: Álison Soares, Rodrigo Avancini Lara e Samuel Huff Dieterich

A equação de Fokker-Planck foi aplicada em primeiro modo em problemas relacionados ao movimento Browniano, como veremos à seguir. Nesse caso, lidando com flutuações originadas de vários pequenos distúrbios, as partículas de interesse se chocavam com as moléculas do meio, provocando uma trajetória probabilística - isto é - não é possível descrever a evolução da partícula sem a observação. Porém, é possível determinar a probabilidade de encontrá-las em determinada região do espaço.

Esta equação pode ser obtida a partir da equação de Langevin e fornece a probabilidade de encontrar determinada partícula em uma posição (varia conforme a dimensionalidade do problema) em um certo instante $t$. Além disso, no presente trabalho temos como objetivo estudar a solução numérica da equação para um dado exemplo com duas variáveis para o espaço de fase mais o tempo, através do método FTCS explícito.

Introdução

Movimento browniano

O movimento browniano foi descoberto pelo botanista Robert Brown, em 1827. Durante seu estudo sobre vida microscópica, ele percebeu pequenas partículas de pólen de plantas se movendo de maneira aleatória no líquido que ele estava estudando e, notando que se tratava de partículas de sujeira, e não seres vivos, chegou a conclusão que era um fenômeno físico, e não biológico, que causava este movimento.

Posteriormente, foi provado que este fenômeno se dava pelos efeitos do movimento molecular. Em um meio com uma temperatura qualquer $>0K$, há vibração e movimento molecular. Embora haja conservacão de energia, quando a partícula interage com as moléculas do meio, a energia cinética desta partícula se altera (assim como a das moléculas). Contudo, a soma destas energias é a energia interna do fluido, como descreve o Teorema da Equiparação.

Em 1905, Albert Einstein propôs uma teoria para descrever tal movimento matematicamente. Primeiramente, ele se propôs a descrever o quão longe uma partícula browniana se desloca em um determinado intervalo de tempo. Como a partícula está sujeita a $10^{14}$ colisões por segundo (provindas das moléculas do meio), a mecânica clássica é incapaz de resolver este sistema . Para resolver este problema, ele abordou o problema pela ótica da mecânica estatística.

Inicialmente, ele considerou o incremento da posição da partícula num espaço unidimensional ($x$), num determinado intervalo de tempo ($\tau$). Considerando que existe uma probabilidade aleatória da partícula se mover dentro do intervalo $\tau$, ele definiu uma função para a densidade de probabilidade ($\varphi (\Delta x)$). Sabendo que o número de partículas é constante dentro do meio, ele expandiu a densidade ($\rho$) deste em uma série de Taylor:

$\rho (x,t)+\tau \left({\frac {\partial \rho (x,t)}{\partial t}}\right)+\dots =\rho (x,t+\tau )=\int _{-\infty }^{+\infty }\rho (x+\Delta x,t)\cdot \varphi (\Delta x)d\Delta x$

que é, por definição, $\varphi$. Continuando,

$=\rho (x,t)\cdot \int _{-\infty }^{+\infty }\varphi (\Delta x)d\Delta x+{\frac {\partial \rho }{\partial x}}\cdot \int _{-\infty }^{+\infty }\Delta x\cdot \varphi (\Delta x)d\Delta x+{\frac {\partial ^{2}\rho }{\partial x^{2}}}\int _{-\infty }^{+\infty }{\frac {\Delta x}{2}}\cdot \varphi (\Delta x)d\Delta x+\dots .$

Pela definição da probabilidade,

$\int _{-\infty }^{+\infty }\varphi (\Delta x)d\Delta x=1$

e as integrais dos termos pares da série são nulos devido à simetria do espaço.

Temos então,

${\begin{alignedat}{2}\rho (x,t+\tau )&=\rho (x,t)\cdot 1+0+{\frac {\partial ^{2}\rho }{\partial x^{2}}}\int _{-\infty }^{+\infty }{\frac {\Delta x}{2}}\cdot \varphi (\Delta x)d\Delta x+\dots \\&=\rho (x,t)+{\frac {\partial ^{2}\rho }{\partial x^{2}}}\int _{-\infty }^{+\infty }{\frac {\Delta x}{2}}\cdot \varphi (\Delta x)d\Delta x+\dots .\end{alignedat}}$

Esta equação nos leva à igualdade

${\frac {\partial \rho }{\partial t}}={\frac {\partial ^{2}\rho }{\partial x^{2}}}\cdot \int _{-\infty }^{+\infty }{\frac {\Delta x}{2}}\cdot \varphi (\Delta x)d\Delta x+{\mathcal {O}}.$

Podemos interpretar a integral como o coeficiente de difusão $D$:

$D=\int _{-\infty }^{+\infty }{\frac {\Delta x}{2}}\cdot \varphi (\Delta x)d\Delta x.$

O que nos dá a equação da difusão

${\frac {\partial \rho }{\partial t}}=D{\frac {\partial ^{2}\rho }{\partial x^{2}}}$

Equação de Langevin

Em 1908, 3 anos após os estudos de Albert Einstein em processos aleatórios e movimento aleatório, Paul Langevin (1872-1946) apresentou um novo método para o movimento browniano que - segundo Langevin - era "infinitamente mais simples" que a solução proposta por Einstein. Para interpretar o movimento browniano, Einstein derivou e resolveu uma equação diferencial parcial descrevendo a evolução temporal da densidade de probabilidade para a partícula. Já Langevin aplicou a segunda lei de Newton na forma diferencial para essa partícula.

Para uma partícula browniana de massa $m$ em um líquido com viscosidade $\eta$, existem duas forças que agem sobre o seu movimento:

1. Arrasto pela viscosidade.

2. Força de flutuação.

Considerando que a partícula é relativamente grande em comparação com as distâncias médias entre as moléculas do líquido e esta se movimento nesse meio com velocidade $v$, experimenta uma resistência pela viscosidade. Essa força é descrita pela Lei de Stokes que, para uma partícula esférica com diâmetro $a$, corresponde a $-6\pi \eta a\ dx/dt$.

A segunda força foi proposta por Langevin para descrever o efeito de constantes impactos das moléculas do líquido sobre as partículas de estudo. Assim, como esta força ($R(t)$) possui uma origem aleatória, essa deveria ser positiva ou negativa de maneira equiprovável e cuja magnitude fosse suficiente para manter a agitação da partícula. Caso contrário, a viscosidade iria parar o movimento dessa partícula.

Com isso, a equação que descreve o movimento a partir da posição da partícula - em 1D na direção $x$ - é dado pela Lei de Newton como:

$m{\frac {d^{2}x}{dt^{2}}}=-\gamma {\frac {dx}{dt}}+R(t)$

onde $m$ é a massa da partícula, $\gamma >0$ é o coeficiente de fricção devido a viscosidade do líquido e $R$ é postulado a força de Langevin representando o efeito das colisões das moléculas do fluído.

Essa equação é conhecida como a equação de Langevin e foi o primeiro exemplo de equação diferencial estocástica, isto é, uma equação diferencial com um termo, $R(t)$ nesse caso, cuja solução em algum sentido também é uma função aleatória . Essa função foi desenvolvida para possuir as seguintes propriedades:

$\langle R(t)\rangle =0\qquad \langle R(t)R(t')\rangle =D\cdot \delta (t-t'),$

onde $\langle f\rangle$ descreve o valor médio ou esperado de uma função $f$, $D$ é o coeficiente de difusão e $\delta$ é a função delta.

A primeira propriedade afirma que o movimento é aleatório de forma que não existe nenhuma tendência de sentido para a partícula se locomover. Assim, é dito que $R(t)$ se trata de um ruído branco gaussiano. Já a segunda propriedade mostra que a força em um dado tempo $t$ é descorrelacionada de uma força para qualquer outro tempo $t'$ (propriedade de Markov).

Dedução da equação de Fokker-Planck

Para a dedução foi utilizado a seguinte referência como base: From Langevin to Fokker-Planck equation.

Como vimos anteriormente, o movimento browniano pode ser descrito pela equação de Langevin, a qual podemos resolver sem nenhum problema. Contudo, alternativamente, podemos fazer uso da equação de Fokker-Planck e considerar uma densidade de probabilidade em relação a posição e o tempo, levando em conta diferentes perturbações estocásticas. Para isso, iremos agora deduzir essa equação, a partir da analise de Langevin.

A descrição do movimento browniano foi anteriormente tratada em termos da equação

$m{\frac {d^{2}x}{dt^{2}}}=-\gamma {\frac {dx}{dt}}+R(t)$

onde $m$ é a massa da partícula, $\gamma >0$ é o coeficiente de fricção devido a viscosidade do líquido e $R$ é postulado a força de Langevin.

Para o nosso propósito, realizaremos uma abordagem mais direta e geral, assumindo a equação de Langevin através de um potencial $U(x)$, nos deixando com a seguinte expressão:

${\frac {dx}{dt}}=-\mu {\frac {dU}{dx}}+\eta (t),$

onde $\mu ={\frac {1}{6\pi \eta a}}$ e $\eta (t)=\mu R(t)$.

Contudo, para entender as equações diferenciais estocásticas, precisamos discretizar as equações para posteriormente aplicar os métodos numéricos. Temos que o sistema de discretização mais simples possível nos leva ao valor de $x$ no tempo $t+\varepsilon$ a partir da interação

$x(t+\varepsilon )=x(t)-\mu {\frac {dU}{dx}}\varepsilon +\eta _{\varepsilon }(t).$

A tarefa é compreender como o agora ruído gaussiano $\eta _{\varepsilon }(t)$ afeta esse sistema discretizado. Para isso, escreveremos a evolução temporal da distribuição de probabilidade $\rho (x,t)$ definida como a probabilidade da partícula estar em $x$ no tempo $t$. Então, deve-se olhar para o limite $t\rightarrow \infty$ de $\rho (x,t)$. Vamos realizar a tarefa com a equação discretizada de Langevin comentada acima. Por razões de simplificação, discutiremos essa abordagem com a forma

$x(t+\varepsilon )=x(t)+v(x)\varepsilon +\eta _{\varepsilon }(t)$

onde Falhou ao verificar gramática (erro de sintaxe): {\displaystyle v(x) \equiv −\mu \frac{dU}{dx}} .

A equação da probabilidade $\rho (x,t)$ pode ser derivada usando a equação de Chapman-Kolmogorov, a qual também iremos escrever em uma forma discretizada no tempo, da forma

$\rho (x,t+\varepsilon )=\int _{-\infty }^{+\infty }W(x,y;\varepsilon )\rho (y,t)dy$

onde $W(x,y;\varepsilon )$ é a probabilidade de que a partícula se mova para $x$ no instante $t+\varepsilon$, desde que tenha começado em $y$ no instante $t$.

Lembrando que: para que a condição acima mova a partícula de $y$ a $x$ no tempo $\varepsilon$, o termo de ruído deve ter apenas o valor correspondente que satisfaz a equação

$x=y+v(y)\varepsilon +\eta _{\varepsilon }(t).$

A probabilidade de $\eta _{\varepsilon }(t)$ acima é dada a partir da distribuição de probabilidade do incremento estocástico $\eta {\varepsilon }$

$\rho _{G}(\eta \varepsilon )={\frac {1}{\sqrt {4\pi D\varepsilon }}}\exp \left({\frac {-\eta _{\varepsilon }^{2}}{4D\varepsilon }}\right),$

Assim $W(x,y;\varepsilon )$ é obtido como

Falhou ao verificar gramática (função desconhecida '\begin{alignat}'): {\displaystyle \begin{alignat}{2} W(x,y; \varepsilon) & = \rho_{G} (\eta_{\varepsilon} = x − y − v(y)\varepsilon) \\ & = \frac{1}{\sqrt{4\pi D\varepsilon}} \exp\left({\frac{−[x−y−v(y)\varepsilon]^2}{4Dε}}\right). \end{alignat} }

Substituindo o $W(x,y;\varepsilon )$ acima na equação de Chapman-Kolmogorov discretizada e expandindo o lado esquerdo para $\varepsilon$, temos

$\rho (x,t)+\partial _{t}\rho (x,t)\varepsilon =\int _{-\infty }^{+\infty }{\frac {\exp \left({\frac {-[x-y-v(y)\varepsilon ]^{2}}{4D\varepsilon }}\right)}{\sqrt {4\pi D\varepsilon }}}\rho (y,t)dy$

Como último passo agora, vamos expandir a integral do lado direito para ordenar $\varepsilon$. Notamos que quando $\varepsilon \rightarrow 0$, a Gaussiana vai para uma função delta e a integral resulta em $\rho (x,t)$ que irá se cancelar com $\rho (x,t)$ no lado esquerdo. Ao final, quando reorganizamos os termos, temos a seguinte equação denominada de Equação de Fokker-Planck

${\frac {\partial \rho (x,t)}{\partial t}}=-{\frac {\partial v(x)\rho (x,t)}{\partial x}}+D{\frac {\partial ^{2}\rho (x,t)}{\partial x^{2}}}$

ou, se substituirmos $v(x)$ pelo potencial Falhou ao verificar gramática (erro de sintaxe): {\displaystyle v(x) = −\mu \partial U(x)/\partial x} , temos que

${\frac {\partial \rho (x,t)}{\partial t}}={\frac {\partial }{\partial x}}{\frac {\partial U}{\partial x}}\rho (x,t)+D{\frac {\partial ^{2}\rho (x,t)}{\partial x^{2}}}$

onde, em ambos os casos, $D$ é o coeficiente de difusão no movimento browniano, com valor $D=\mu k_{B}T={\frac {k_{B}T}{6\pi \eta a}}$, cujas variáveis foram discutidas anteriormente na equação de Langevin.

Esta distribuição pode ainda depender de um conjunto de $N$ macrovariáveis $x_{i}$, de tal maneira que o movimento browniano em questão pode ser representado por uma equação de Fokker-Planck da forma :

${\frac {\partial \rho (x,t)}{\partial t}}=-\left[\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}D_{i}^{1}(x_{1},...,x_{N})+\sum _{i=1}^{N}\sum _{j=1}^{N}{\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}D_{ij}^{2}(x_{i},...,x_{N})\right]\rho ,$

onde $D^{1}$ é o termo que é dado por um vetor e $D^{2}$ é o termo de difusão, dado por uma matriz.

Exemplos: acelerador de partículas

O exemplo e explicações trazidas nessa seção foram retirados do artigo: Numerical solution of two dimensional Fokker-Planck equations .

Uma aplicação amplamente utilizada para a equação de Fokker-Planck como uma Equação Diferencial Estocástica (Stochastic Differential Equations, SDE) é para a modelagem da dinâmica de partículas únicas em aceleradores sob influência de ruído. As fontes de ruído são, por exemplo, campos aleatórios, movimento aleatório do solo ou flutuações quânticas da radiação.

A partir do cálculo de probabilidade fornecido pela equação de Fokker-Planck, algumas propriedades físicas de interesse são: qual é o comportamento de longo prazo da dinâmica; qual a probabilidade da partícula colidir com a câmara de vácuo e então ser perdida; quais são as flutuações médias da partícula em torno da trajetória do acelerador; e qual é a evolução temporal da densidade de probabilidade?

Para responder essas perguntas, apenas alguns casos mais específicos possuem soluções analíticas, especialmente em problemas com maior dimensionalidade. Por esse motivo, é interessante e prático estudar a equação de Fokker-Planck e os problemas relacionados a partir de métodos numéricos.

Para esse fim, serão abordados dois exemplos: o oscilador harmônico amortecido, o qual possuí solução analítica e poderá ser usado como comparação para verificar a acurácia do método; e o problema de Duffing, oscilador não linear, com amortecimento e ruído multiplicativo e aditivo, que não apresenta solução exata.

Equações

As equações diferenciais típicas encontradas na física do acelerador de partícula são

${\begin{cases}{\dot {x}}=v,\\{\dot {v}}=-a_{1}(x)-a_{2}(x,v)+{\sqrt {2\sigma }}R(t),\end{cases}}$

onde $R(t)$ é o ruído branco gaussiano e $\sigma$ é uma constante.

Para o caso do oscilador harmônico amortecido e com ruído, temos

${\begin{cases}{\dot {x}}=v,\\{\dot {v}}=-Kx-\gamma v+{\sqrt {2\sigma }}R(t),\end{cases}}$

onde $K$ e $\gamma$ também são constantes.

Já para o oscilador estocástico de Duffing, não-linear, com amortecimento, ruído multiplicativo e aditivo temos

${\begin{cases}{\dot {x}}=v,\\{\dot {v}}=-\omega ^{2}\left[\left(\alpha +{\sqrt {2D_{11}}}R_{1}(t)\right)x+\epsilon x^{3}\right]-2\tau \omega {\dot {x}}+{\sqrt {2D_{22}}}R_{2}(t),\end{cases}}$

onde $\omega$, $\alpha$, $\epsilon$, $\tau$, $D_{11}$ e $D_{22}$ são constantes dadas.

Escrevendo esses exemplos em termos da equação de Fokker-Planck obtemos

${\frac {\partial \rho }{\partial t}}=-{\frac {\partial v}{\partial x}}\rho +{\frac {\partial }{\partial v}}\left(\gamma v+Kx+\sigma {\frac {\partial }{\partial v}}\right)\rho$

para o primeiro caso e

${\frac {\partial \rho }{\partial t}}=-{\frac {\partial v}{\partial x}}\rho +{\frac {\partial }{\partial v}}[(a_{1}(x)+a_{2}(x,v))\rho ]+{\frac {1}{2}}{\frac {\partial ^{2}}{\partial v^{2}}}(2D\rho )$

$a_{1}(x)=\omega ^{2}x(\alpha +\epsilon x^{2}),\quad a_{2}(x,v)=2\tau \omega v,\quad D=D_{11}\omega ^{4}x^{2}+D_{22}$

para o segundo exemplo.

Método FTCS explícito

Para os fins de estudo desses casos, o método numérico mais simples para descrever a função $\rho$ é a partir do FTCS (Foward Time Central Space) explícito . Como ficará mais claro a partir da discretização das equações, o método FTCS calcula o resultado de uma função no tempo seguinte em um dado ponto a partir dos valores dos "vizinhos" desse ponto. Para a técnica explícita, podemos calcular valor da função no tempo $n+1$ a partir apenas de valores já conhecidos no tempo atual $n$. Assim, a aplicação do método se torna bem simples, contudo, perdemos precisão/estabilidade em comparação com métodos mais sofisticados.

O primeiro passo para o método é discretizar os termos da função de interesse $\rho (x,v,t)$ nas derivadas parciais necessárias: $\partial /\partial x$, $\partial /\partial v$, $\partial ^{2}/\partial v^{2}$. Para isso, usamos a expansão da série de Taylor e, para melhor precisão, a derivada centrada (excluindo a derivada no tempo). Ademais, usaremos a notação dos índices para indicar os valores de $x$, $v$ e $t$ por $i$, $j$ e $n$, respectivamente.

${\frac {\partial \rho }{\partial t}}\rightarrow {\frac {\rho (x,v,t+\Delta t)-\rho (x,v,t)}{\Delta t}}+{\mathcal {O}}(\Delta t^{2})\rightarrow {\frac {\rho _{i,j}^{n+1}-\rho _{i,j}^{n}}{\Delta t}}$

${\frac {\partial \rho }{\partial x}}\rightarrow {\frac {1}{2}}\left[{\frac {\rho (x+\Delta x,v,t)-\rho (x,v,t)}{\Delta x}}+{\frac {\rho (x-\Delta x,v,t)-\rho (x,v,t)}{\Delta x}}\right]+{\mathcal {O}}(\Delta x^{2})\approx {\frac {\rho (x+\Delta x,v,t)-\rho (x-\Delta x,v,t)}{2\Delta x}}\rightarrow {\frac {\rho _{i+1,j}^{n}+\rho _{i-1,j}^{n}}{2\Delta x}}$

${\frac {\partial \rho }{\partial v}}\rightarrow {\frac {1}{2}}\left[{\frac {\rho (x,v+\Delta v,t)-\rho (x,v,t)}{\Delta v}}+{\frac {\rho (x,v,t)-\rho (x,v-\Delta v,t)}{\Delta v}}\right]+{\mathcal {O}}(\Delta v^{2})\approx {\frac {\rho (x,v+\Delta v,t)-\rho (x,v-\Delta v,t)}{2\Delta v}}\rightarrow {\frac {\rho _{i,j+1}^{n}+\rho _{i,j-1}^{n}}{2\Delta v}}$

${\frac {\partial ^{2}\rho }{\partial v^{2}}}\rightarrow {\frac {\rho (x,v+\Delta v,t)-2\rho (x,v,t)+\rho (x,v-\Delta v,t)}{(\Delta v)^{2}}}+{\mathcal {O}}(\Delta v^{3})\rightarrow {\frac {\rho _{i,j+1}^{n}-2\rho _{i,j}^{n}+\rho _{i,j-1}^{n}}{(\Delta v)^{2}}}$

Aplicação

Com as derivadas parciais discretizadas, podemos agora reescrever as funções de Fokker-Planck para cada caso de estudo em busca do valor de $\rho _{i,j}^{n+1}$, isto é, o valor de cada ponto no espaço $xv$ para o tempo $t+\Delta t$.

Caso 1: oscilador harmônico amortecido

Primeiramente, reescrevemos a função original expandindo os termos e aplicando a regra da cadeia onde for necessário.

${\begin{alignedat}{2}{\frac {\partial \rho }{\partial t}}&=-{\frac {\partial v}{\partial x}}\rho +{\frac {\partial }{\partial v}}\left(\gamma v+Kx+\sigma {\frac {\partial }{\partial v}}\right)\rho \\[1em]&=-{\frac {\partial }{\partial x}}(v\rho )+{\frac {\partial }{\partial v}}(\gamma v+Kx)\rho +\sigma {\frac {\partial ^{2}}{\partial v^{2}}}\rho \\[1em]&=-v{\frac {\partial }{\partial x}}\rho +{\frac {\partial }{\partial v}}(\gamma v\rho )+{\frac {\partial }{\partial v}}(Kx\rho )+\sigma {\frac {\partial ^{2}}{\partial v^{2}}}\rho \\[1em]&=-v{\frac {\partial }{\partial x}}\rho +\gamma \rho +\gamma v{\frac {\partial }{\partial v}}\rho +Kx{\frac {\partial }{\partial v}}\rho +\sigma {\frac {\partial ^{2}}{\partial v^{2}}}\rho \\[1em]&=-v{\frac {\partial }{\partial x}}\rho +\gamma \rho +(\gamma v+Kx){\frac {\partial }{\partial v}}\rho +\sigma {\frac {\partial ^{2}}{\partial v^{2}}}\rho \end{alignedat}}$

Agora, reescrevemos a mesma função substituindo as derivadas parciais e demais variáveis necessárias ($x$) pelas versões discretizadas.

${\frac {\rho _{i,j}^{n+1}-\rho _{i,j}^{n}}{\Delta t}}=-v\left({\frac {\rho _{i+1,j}^{n}-\rho _{i-1,j}^{n}}{2\Delta x}}\right)+\gamma \rho _{i,j}^{n}+(\gamma v+Kx^{n})\left({\frac {\rho _{i,j+1}^{n}-\rho _{i,j-1}^{n}}{2\Delta v}}\right)+\sigma \left({\frac {\rho _{i,j+1}^{n}-2\rho _{i,j}^{n}+\rho _{i,j-1}^{n}}{(\Delta v)^{2}}}\right)$

$\rho _{i,j}^{n+1}=\rho _{i,j}^{n}+\Delta t\left[-v\left({\frac {\rho _{i+1,j}^{n}-\rho _{i-1,j}^{n}}{2\Delta x}}\right)+\gamma \rho _{i,j}^{n}+(\gamma v+Kx^{n})\left({\frac {\rho _{i,j+1}^{n}-\rho _{i,j-1}^{n}}{2\Delta v}}\right)+\sigma \left({\frac {\rho _{i,j+1}^{n}-2\rho _{i,j}^{n}+\rho _{i,j-1}^{n}}{(\Delta v)^{2}}}\right)\right]$

Para exercício, usaremos um $v$ constante de forma que apenas será necessário atualizar a variável $x$ para cada passo de tempo.

$x^{n+1}=x^{n}+v\Delta t$

Por fim, é necessário definir uma condição inicial e uma condição de contorno. Uma vez que a função descreve uma densidade de probabilidade, a literatura sugere, até para comparar com a solução analítica quando disponível, uma delta de Kronecker $\delta (x-x_{0},v-v_{0})$. Assim, em uma dada coordenada $(x,v)$ no tempo $t_{0}$ teremos uma probabilidade 1 de encontrar a partícula. Como condição de contorno, dado que a função em um dado ponto precisa dos pontos vizinhos, indicamos que a "borda" da matriz será sempre igual a zero.

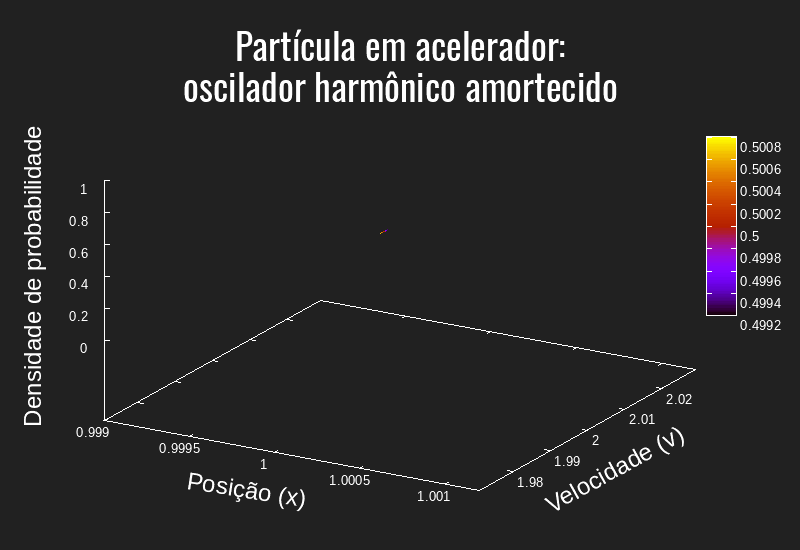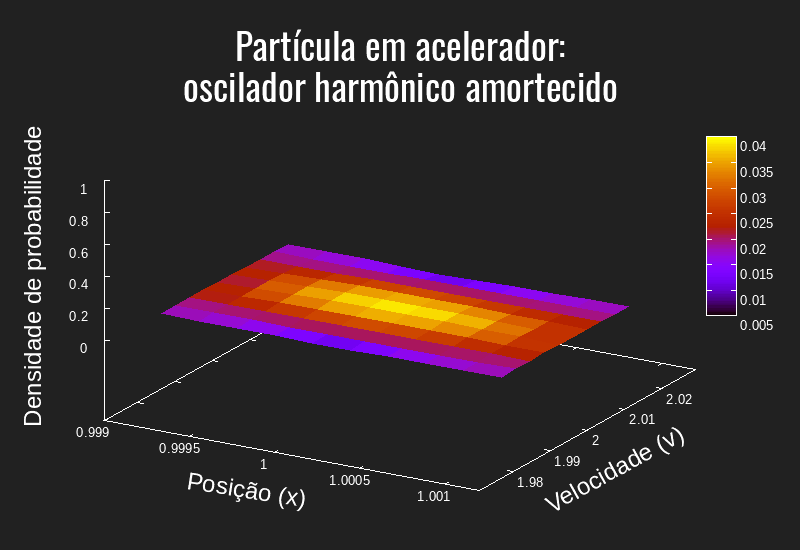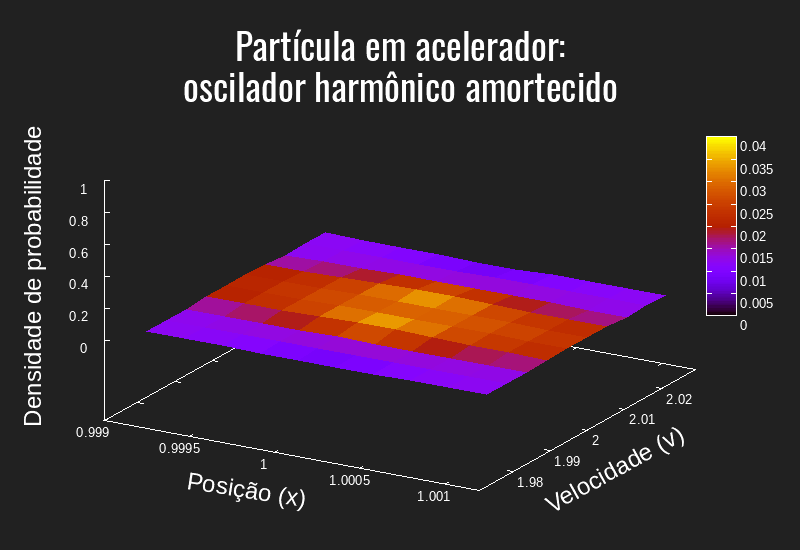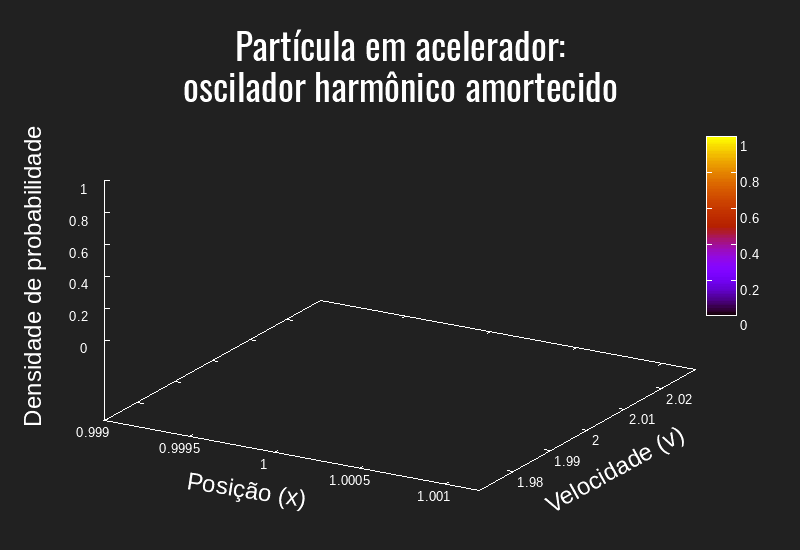
Dado essas equações, escrevemos um programa em C para gerar os dados e o gnuplot para criar o gráfico/animação. Os códigos desenvolvidos estarão disponíveis na próxima seção "Código desenvolvido".

Animação da evolução da probabilidade de encontrar uma partícula com dada posição $x$ e $v$ a partir da equação de um oscilador harmônico amortecido. Valores da animação: $\Delta x=1\times 10^{-3}$, $\Delta v=1\times 10^{-3}$, $\Delta t=1\times 10^{-6}$, $x_{0}=1$, $v=2$, $k=0.5$, $\gamma =0.5$, $\sigma =0.5$.

A partir da referência estudada e da física do problema, é evidente que a animação apresentada está aquém do esperado. Pelos testes pelo grupo responsável por esse documento, o programa desenvolvido se mostrou muito instável e impreciso: alterações mínimas de alguns parâmetros alteravam consideravelmente o resultado observado. Esse comportamento "imprevisível" se tornou ainda evidente ao alterar o tamanho dos passos (dt, dx, dv) de forma que tanto aumentando quanto diminuindo uma ordem de grandeza a função "explodia" - isto é - crescia exponencialmente. Assim, não foi possível aumentar a resolução da "simulação".

Além disso, em alguns casos, a função retornava valores negativos, o que é inadequado para uma densidade de probabilidade. Ademais, a ordem de grandeza para o tempo usada na simulação desse trabalho está muito abaixo da utilizada na referência base para esse problema, mostrando que a evolução temporal pode ter algum problema. No entanto, o problema que destacamos é a falta de "suavidade" na curva gerada, tanto é que em alguns quadros é possível ver mudanças bruscas no formato da função.

Dessa forma, apesar dos esforços da equipe, não fomos capazes - até o momento dessa edição - de encontrar a causa desses problemas. No entanto, segue algumas hipóteses que podem ser avaliadas para futuras revisões deste material:

- Verificar as equações utilizadas para descrever os problemas e a passagem para a equação de Fokker-Planck. A literatura encontrada não apresenta os passos usados para esse cálculo e nem a referência específica para cada etapa. Assim, o grupo precisou confiar que esse artigo estava correto.

- Verificar a discretização da função para o método FTCS explícito.

- Verificar a estabilidade do método, pois, apesar de não ter ser comentado no material de referência, é possível que o método explícito não seja adequado para os casos estudados.

- Verificar possíveis problemas no código, tanto o código para os dados quanto para a visualização.

- Verificar problemas de truncamento ou erro numérico ou ainda valores inadequados para as constantes utilizadas.

Caso 2: problema de Duffing

Assim como no caso anterior, reescrevemos a equação para uma forma conveniente.

${\frac {\partial \rho }{\partial t}}=-{\frac {\partial v}{\partial x}}\rho +{\frac {\partial }{\partial v}}[(a_{1}(x)+a_{2}(x,v))\rho ]+{\frac {1}{2}}{\frac {\partial ^{2}}{\partial v^{2}}}(2D\rho )$

$a_{1}(x)=\omega ^{2}x(\alpha +\epsilon x^{2}),\quad a_{2}(x,v)=2\tau \omega v,\quad D=D_{11}\omega ^{4}x^{2}+D_{22}$

${\begin{alignedat}{2}{\frac {\partial \rho }{\partial t}}&=-{\frac {\partial v}{\partial x}}\rho +{\frac {\partial }{\partial v}}[\omega ^{2}x(\alpha +\epsilon x^{2})+2\tau \omega v]\rho +{\frac {\partial ^{2}}{\partial v^{2}}}(D_{11}\omega ^{4}x^{2}+D_{22})\rho \\[1em]&=-v{\frac {\partial }{\partial x}}\rho +[\omega ^{2}x(\alpha +\epsilon x^{2})+2\tau \omega v]{\frac {\partial }{\partial v}}\rho +2\tau \omega \rho +(D_{11}\omega ^{4}x^{2}+D_{22}){\frac {\partial ^{2}}{\partial v^{2}}}\rho \end{alignedat}}$

Novamente, substituímos os termos necessários pela forma discretizada.

${\frac {\rho _{i,j}^{n+1}-\rho _{i,j}^{n}}{\Delta t}}=-v\left({\frac {\rho _{i+1,j}^{n}-\rho _{i-1,j}^{n}}{2\Delta x}}\right)+[\omega ^{2}{x^{n}}(\alpha +\epsilon {x^{n}}^{2})+2\tau \omega v]{\frac {\rho _{i,j+1}^{n}+\rho _{i,j-1}^{n}}{2\Delta v}}+2\tau \omega \rho _{i,j}^{n}+(D_{11}\omega ^{4}{x^{n}}^{2}+D_{22}){\frac {\rho _{i,j+1}^{n}-2\rho _{i,j}^{n}+\rho _{i,j-1}^{n}}{(\Delta v)^{2}}}$

$\rho _{i,j}^{n+1}=\rho _{i,j}^{n}+\Delta t\left\{-v\left({\frac {\rho _{i+1,j}^{n}-\rho _{i-1,j}^{n}}{2\Delta x}}\right)+[\omega ^{2}{x^{n}}(\alpha +\epsilon {x^{n}}^{2})+2\tau \omega v]{\frac {\rho _{i,j+1}^{n}+\rho _{i,j-1}^{n}}{2\Delta v}}+2\tau \omega \rho _{i,j}^{n}+(D_{11}\omega ^{4}{x^{n}}^{2}+D_{22}){\frac {\rho _{i,j+1}^{n}-2\rho _{i,j}^{n}+\rho _{i,j-1}^{n}}{(\Delta v)^{2}}}\right\}$

Considerando mais uma vez que a velocidade da partícula será constante,podemos atualizar o valor de $x$ pela expressão: $x^{n+1}=x^{n}+v\Delta t$.

Para condições iniciais e condições de contorno, usamos o mesmo princípio definido no caso anterior: condição inicial dada por $\delta (x-x_{0},v-v_{0})$ e condição de contorno definindo as "paredes" com valor zero para qualquer tempo $t$.

Uma vez que o grupo não foi capaz de encontrar bons resultados para o caso anterior (mais simples), não foi desenvolvido nenhum código para esse exemplo até que o problema anterior fosse resolvido. Esperamos que em uma futura edição esse material possa trazer alguma visualização para o caso com ruído aditivo e multiplicativo descrito pelo problema de Duffing.

Código desenvolvido

Função auxiliar utilizada do arquivo de cabeçalho pointers.h:

double ***create_3d_double_pointer(int x, int y, int z){
  double ***pointer;
  int i, j;

  assert((x > 0) && (y > 0) && (z > 0));
  pointer = (double ***)malloc(x * y * z * sizeof(double **));
  if (pointer == NULL){
    fprintf(stderr, "Error in routine create_3d_double_pointer\n");
    exit(8);
  }
  else {
    for (i = 0; i < x; i++){
      pointer[i] = (double **)malloc(y * z * sizeof(double *));
      if (pointer[i] == NULL){
        fprintf(stderr, "Error in routine create_3d_double_pointer\n");
        exit(8);
      }
    }
    for (i = 0; i < x; i++){
      for (j = 0; j < y; j++){
        pointer[i][j] = (double *)malloc(z * sizeof(double));
        if (pointer[i][j] == NULL){
          fprintf(stderr, "Error in routine create_3d_double_pointer\n");
          exit(8);
        }
      }
    }
  }
  return (pointer);
}

Código utilizado para gerar os dados para o "caso 1".

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "pointers.h"

int main(){

  // Declara as variáveis
  FILE *fp;
  char output[50];
  double ***f;
  int i, j, k, c, Lx, Lv;
  double time, tmax, dt, dx, dv, v, x, K, gamma, sigma, epsilon; 
  
  // Configura os valores iniciais
  time = 0.0;       // Tempo
  tmax = 0.0001;    // Tempo máximo
  Lx = 50;          // Quantidade de pontos em x
  Lv = 100;         // Quantidade de pontos em v
  dt = 0.000001;    // Passo em t
  dx = 0.001;       // Passo em x
  dv = 0.001;       // Passo em v
  x = 1;            // Posição inicial
  v = 2;            // Velocidade
  K = 0.5;          // Constante
  gamma = 0.5;      // Constante
  sigma = 0.5;      // Constante
  epsilon = 10E-4;  // Valor para comparação

  // Inicializa a matriz 3D
  f = create_3d_double_pointer(Lx, Lv, 2);
  // Todos os pontos com valores zero
  for (i=0; i<Lx; i++){
    for (j=0; j<Lv; j++){
      for (k=0; k<2; k++){
        f[i][j][k] = 0.0;
      }
    }
  }

  // Condição inicial
  f[Lx/2][Lv/2][0] = 1.0;

  // Arquivo para output
  sprintf(output, "caso1.dat");
  fp = fopen(output, "w");

  c = 0;
  // Loop da "simulação"
  while (time<tmax){
    for (i=1; i<(Lx-1); i++){
      for (j=1; j<(Lv-1); j++){
        // Atualiza a probabilidade
        f[i][j][1-c] = f[i][j][c]+dt*(-v*(f[i+1][j][c]-f[i-1][j][c])/(2*dx)+gamma*f[i][j][c]+(gamma*v+K*x)*(f[i][j+1][c]-f[i][j-1][c])/(2*dv)+sigma*(f[i][j+1][c]-2*f[i][j][c]+f[i][j-1][c])/(dv*dv));
        // Salva o resultado em arquivo
        if (fabs(f[i][j][1-c]) > epsilon){
          fprintf(fp, "%f %f %f\n", (double)(i-Lx/2)*dx+x, (double)(j-Lv/2)*dv+v, f[i][j][1-c]);
        }
      }
      // Adiciona linha em branco (arquivo XYZ - gnuplot)
      if (fabs(f[i][j][1-c]) > epsilon){
        fprintf(fp, "\n");
      }
    }
    // Atualiza a posição
    x = x + v*dt;
    c = 1 - c;
    // Adiciona duas linhas em branco (animação - gnuplot)
    fprintf(fp, "\n\n");
    time += dt;
  }

  fclose(fp); // Fecha arquivo
  free(f);    // Libera ponteiro

  return 0;
}

Código utilizado no gnuplot para gerar a animação.

# Limpa configurações anteriores
unset xrange
unset yrange
unset zrange

# Gera estatísticas dos dados
stats "caso1.dat" name "A"

# Estilo para gráfico
set dgrid3d

# Ponto de vista
set view 60, 30, 1, 1

# Configura o range do plot
set xrange [A_min_x:A_max_x]
set yrange [A_min_y:A_max_y]
set zrange [0:1]

# Formato de saída
set term gif animate delay 25 background "#212121" enhanced font "Arial,10" fontscale 1.0 size 800, 550

set title "Partícula em acelerador:\noscilador harmônico amortecido" offset character 0, -3 font "Oswald,28" tc rgb "white"
set xlabel "Posição (x)" offset character -2, -2 font ",18" tc rgb "white" rotate by -9
set ylabel "Velocidade (v)" offset character -3, -3 font ",18" tc rgb "white" rotate parallel
set zlabel "Densidade de probabilidade" offset character -1.5, -1.5 font ",18" tc rgb "white" rotate parallel

set tics tc rgb "white" offset character -1, -1
set border lc rgb "white"

set output "caso1.gif"

do for [i=0:int(A_blocks-1)] {  
    splot 'caso1.dat' index i with pm3d notitle
    }