Grupo - Tráfego
Integrantes: Rodrigo Zamin Ferreira (262692) e Maurício Gomes de Queiroz (264889)
Introdução
O estudo de caso do comportamento do tráfego urbano se mostra de grande utilidade nos dias atuais, onde metrópoles apresentam grandes volumes de veículos se deslocando pela cidade. Em horários de pico, por exemplo, às 18h, Porto Alegre apresenta média de lentidão de 83km[1], enquanto São Paulo chega a incríveis 485km[2].
A modelagem de tal comportamento permite um estudo das regras básicas que motoristas tendem a seguir em situações reais, levando assim a um melhor entendimento da formação e desenvolvimento de congestionamentos, além da obtenção de outras informações interessantes, como a velocidade média em função do número de carros.
Aqui é proposto um modelo simples do funcionamento normal de uma avenida utilizando autômatos celulares, inicialmente com apenas uma faixa, sendo após estendido para n faixas.
Autômatos Celulares
Weimar[3] define um autômato celular em "Simulation with Cellular Automata", informalmente, como um vetor de células sendo caracterizado pelas seguintes propriedades básicas:
• A evolução se dá em passos discretos de tempo;
• Cada célula é caracterizada por um estado pertencente a um conjunto finito de estados;
• Cada célula evolui de acordo com as mesmas regras que dependem somente do estado em que a célula se encontra e de um número finito de vizinhos;
• A relação com a vizinhança é local e uniforme.
Apesar de simples, autômatos celulares (AC) são capazes de simular sistemas dinâmicos complexos e são extensivamente utilizados aqui, onde cada célula representa uma posição na avenida, que pode conter um veículo ou não. Caso contenha um veículo, a célula possui um estado associado a si que representa o índice do veículo, através do qual podemos acessar sua velocidade, a qual pode assumir valores discretos de 0 a ; caso contrário, a célula possui um estado que indica que está vazia, sendo utilizado o estado -1 para esse objetivo. A velocidade de um carro representa o número de células que o carro andará num passo.
A atualização dos estados é feita de forma não-síncrona (os estados das células são atualizados um após o outro) e homogênea (as regras de atualização não dependem da posição espacial da própria célula, somente da posição relativa dos vizinhos) [4].
A mudança dos estados é feita com base em regras que se baseiam nos estados da vizinhança, tendo também algumas mudanças estocásticas, caracterizando um método de Monte Carlo.
Regras de Aceleração
Estabelecemos as regras de mudança da velocidade com base no artigo de Nagel e Schreckenberg (1992)[5]. São três os casos em que um autômato do modelo descrito aqui muda de velocidade:
Regra 1: A velocidade é reduzida caso a distância entre um carro e o veículo que vai à sua frente seja suficientemente pequena para que haja colisão durante a atualização de posições da simulação, sendo necessária a redução da velocidade para impedir que isso ocorra.
Regra 2: De modo análogo, aumenta-se a velocidade caso a velocidade atual for menor que a máxima e seja suficientemente grande para que não haja colisão durante a atualização de posições da simulação usando a velocidade nova.
Regra 3: É também introduzido no modelo um fator que aleatoriamente reduz a velocidade do veículo, para que seja levado em conta flutuações da velocidade devido ao comportamento humano. Esse passo é essencial, já que sem ele o modelo seria determinístico.
Ou seja, sendo a distância entre um carro e o que está à sua frente, a velocidade do carro, e o tempo de um passo,
Regra 1: Caso , então
Regra 2: Caso , então
Regra 3: Com uma probabilidade ,
Faixa Única
O problema de faixa única, mesmo que simples, gera discussões muito boas quando simulado. O cenário consiste em uma avenida de uma faixa, com células, com carros que se movem da esquerda para a direita, submetidos às regras citadas anteriormente. Além disso, foram utilizadas condições de contorno periódicas, e os carros foram inicializados em posições aproximadamente equidistantes. Os valores dos parâmetros utilizados foram e .
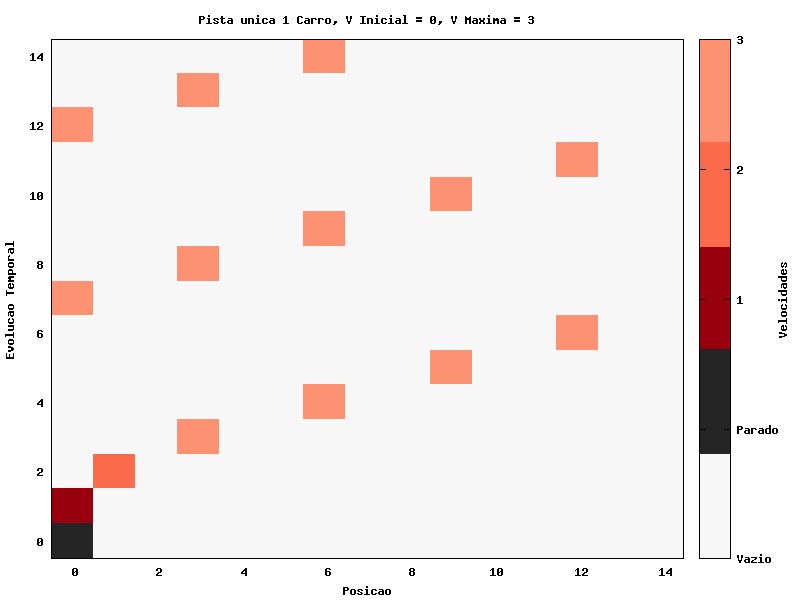
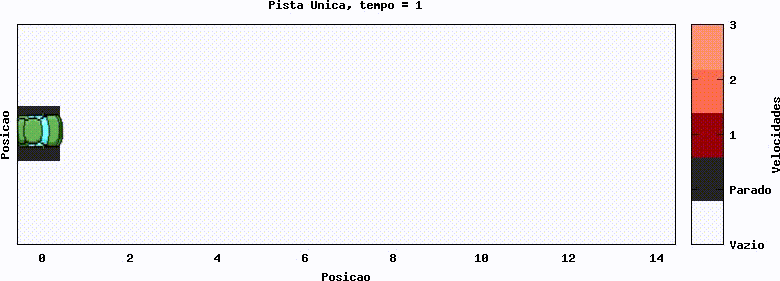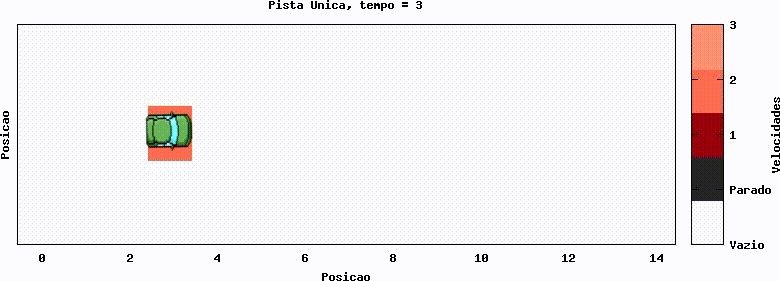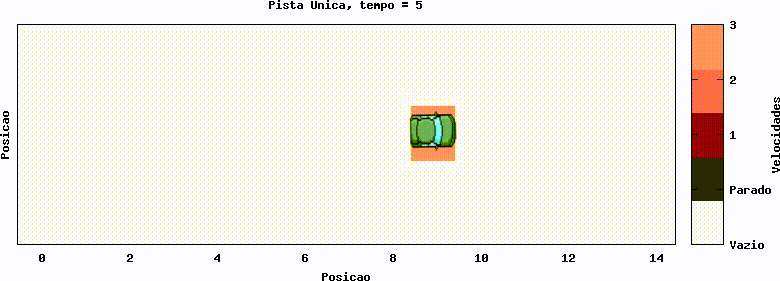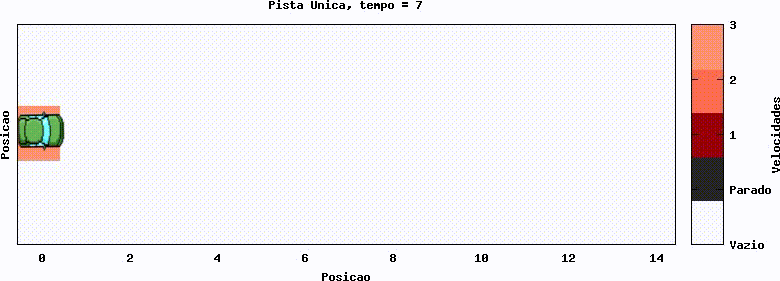
Uma primeira abordagem, com finalidade situar a simulação, é com um único carro, sem implementação da redução de velocidade randômica (Regra 3). No gráfico abaixo, o carro se desloca, partindo do repouso (representado pela cor preta no gráfico) e com aceleração, até atingir a velocidade máxima, com valor 3, que é mantida no decorrer do tempo. Tal gráfico mostra o funcionamento base dos autômatos e da visualização da evolução temporal dos mesmos.
Foi gerado uma simples animação para ilustrar o funcionamento da visualização.
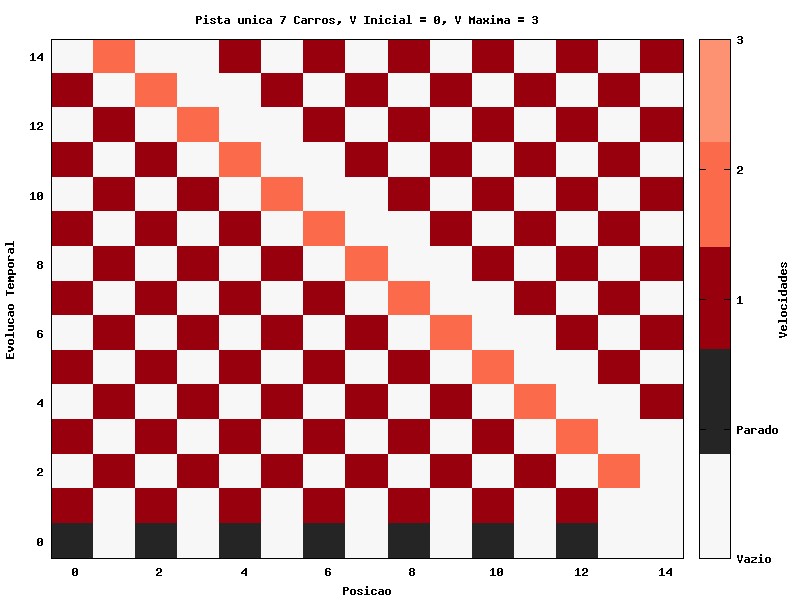
O próximo passo é estendermos o modelo para o caso com 7 carros, isto é, uma densidade de quase 0.5 carros/célula (Gráfico 2).
Observamos que a distância até o próximo carro é 2 para todos os carros (a distância é calculada pela diferença das posições dos carros; embora no gráfico somente haja uma célula entre eles, a distância é 2-0 = 2 para o primeiro carro, por exemplo), exceto para o carro que inicia mais à direita, com distância 3. Por isso ele é o primeiro a alcançar uma velocidade de 2, enquanto os outros estavam a velocidade 1. Esse carro então, percorre essa distância maior do que os demais, ficando a uma distância 2 do veículo à sua frente, enquanto o carro que está atrás dele tem uma distância de 3, podendo agora aumentar sua velocidade para 2, e assim por diante; por isso a zona em que os carros tem velocidade 3 se propaga no sentido contrário do seu movimento.
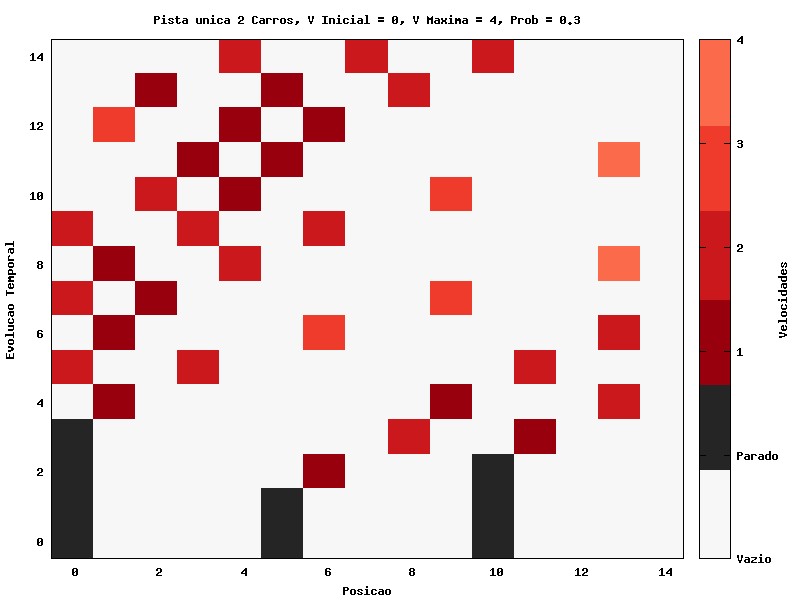
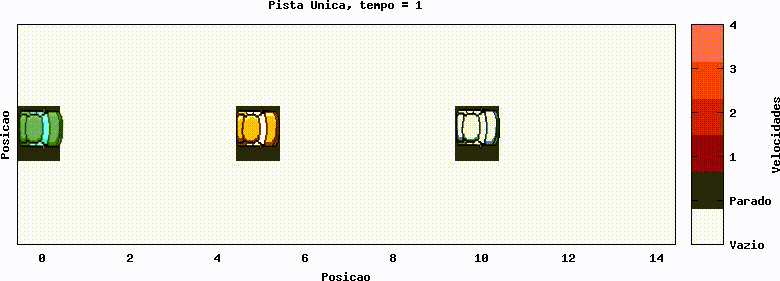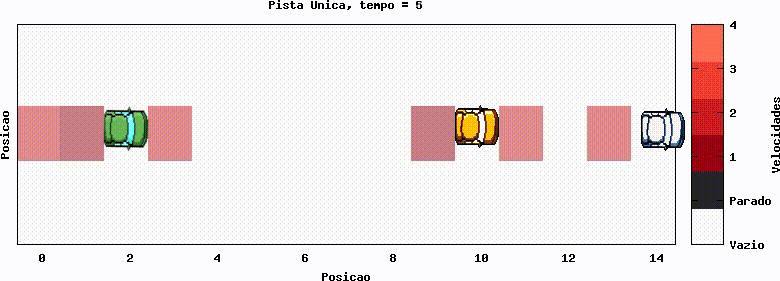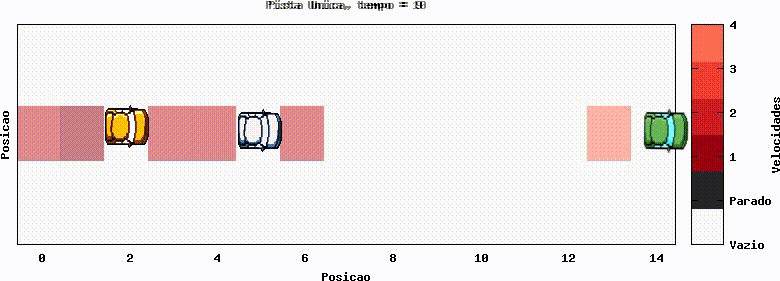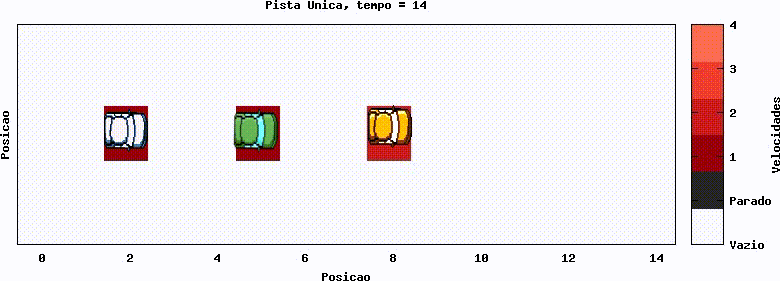
Agora, podemos introduzir a probabilidade de redução de velocidade, em uma situação com dois carros. Percebe-se no gráfico abaixo, por exemplo, que o carro iniciado na posição 0 permanece dois passos de tempo com velocidade 0, enquanto o segundo carro já havia mudado de velocidade, algo causado pela probabilidade de redução da velocidade. Nestes gráficos ainda não há grande redução de velocidade e congestionamentos, já que a densidade é baixa; porém, ao decorrer do tempo, os carros oscilam sua velocidade entre 3 e 2. A probabilidade de redução de velocidade utilizada aqui é a de 0.3, a qual é a mesma para todas as simulações analisadas nesta página. Na próxima seção analisaremos também a influência da variação desse parâmetro na velocidade média.
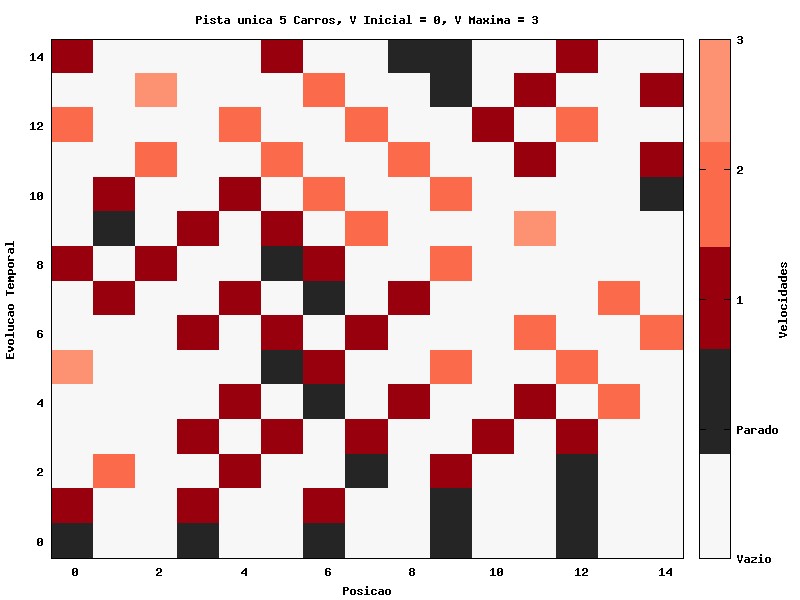
Ao aplicarmos a simulação para 5 carros (Gráfico 4), observamos que já há pontos de lentidão (ou seja, regiões em que os carros se movem com baixa velocidade, representado pela cor vermelho escuro) e congestionamento (trechos que apresentam velocidade zero), causados pela probabilidade de redução da velocidade e maior densidade de carros. Esses trechos se propagam, de acordo com a simulação, contra o sentido de movimentação dos carros.
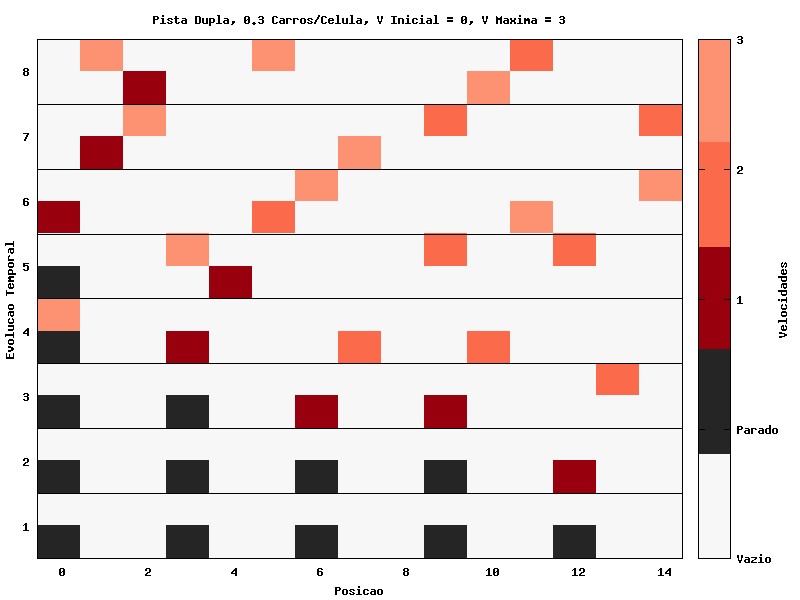
Finalmente, estendemos o modelo para um sistema com , e (Gráfico 5), juntando todas as análise feitas anteriormente.
Após o início, mesmo deixando , os carros permanecem principalmente com velocidade 1 e 2. Além de trechos grandes de congestionameto, trechos menores são espontaneamente criados devido a probabilidade de redução de velocidade. Todos os trechos de lentidão/congestionamento são propagados contra o fluxo dos carros.
Medidas de Velocidade
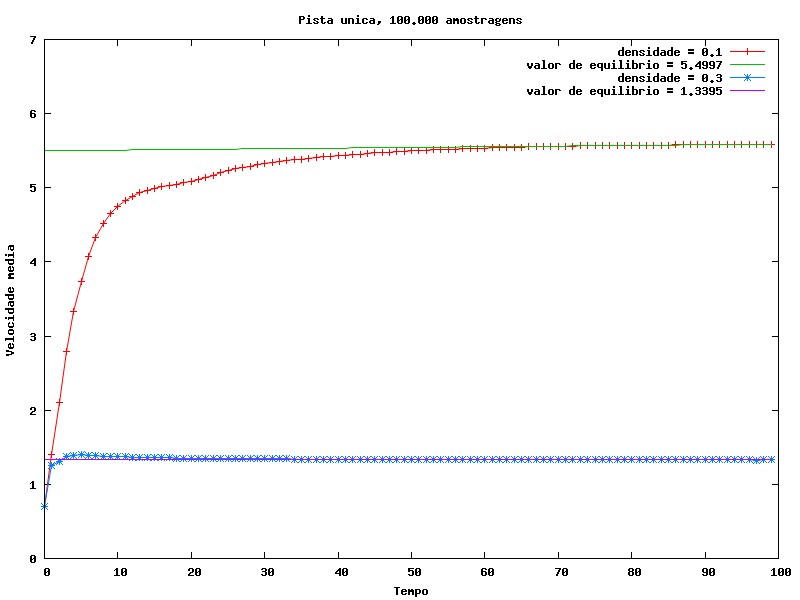
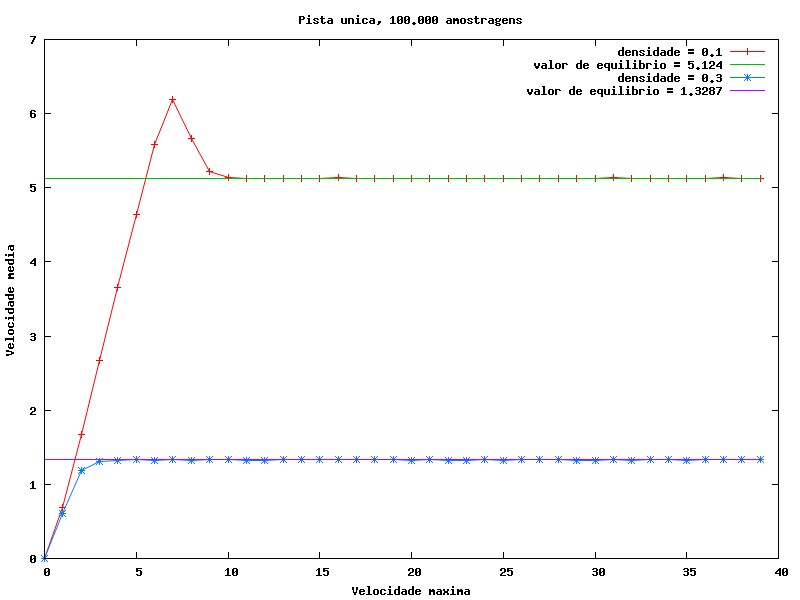
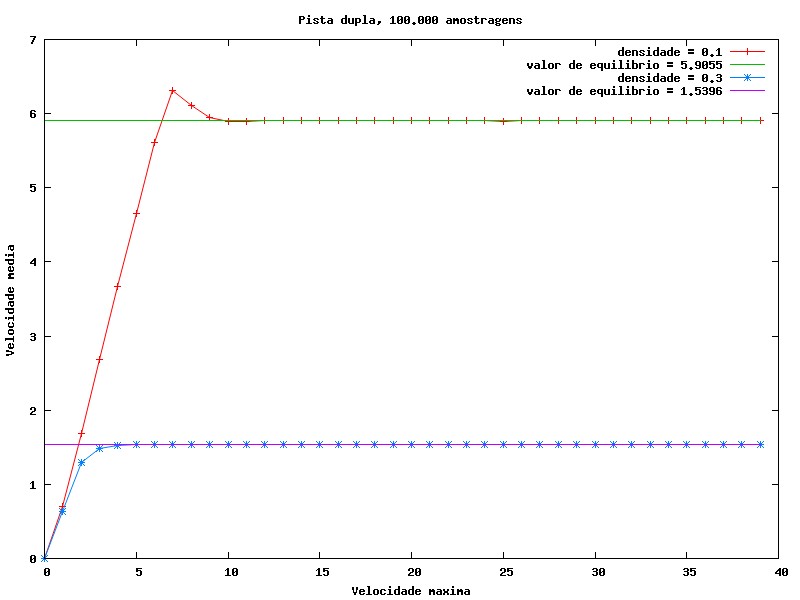
Por fim, foi medida a velocidade média como função do tempo (fixando a velocidade máxima em 6) e como função da velocidade máxima (sendo medida em ) (Gráficos 6 e 7). Com o intuito de fazer uma análise por método de Monte Carlo, somos levados a utilizar grande quantidade de amostragens para obter um resultado, ainda que estimado, mais próximo do real. Aqui são utilizadas 100.000 amostragens e então foi calculada a média da velocidade entre elas. Com mais amostragens reduz-se o ruído, porém o tempo gasto com seu cálculo é significantemente aumentado.
Em ambos os casos, a velocidade média tende a um valor de equilíbrio. Para o caso do Gráfico 7, inicialmente o aumento da velocidade máxima tem grande impacto na velocidade média, mas a medida que a velocidade máxima aumenta, é atingido um ponto em que o aumento da velocidade máxima não é mais significativo para a velocidade média, já que dificilmente os carros atingem velocidades tão altas. O pico que aparece neste gráfico pode ser atribuído ao fato de que uma velocidade máxima mais alta faz com que os carros possam atingir velocidades mais altas, e isso pode fazer com que os carros fiquem mais próximos uns dos outros, diminuindo a velocidade média.
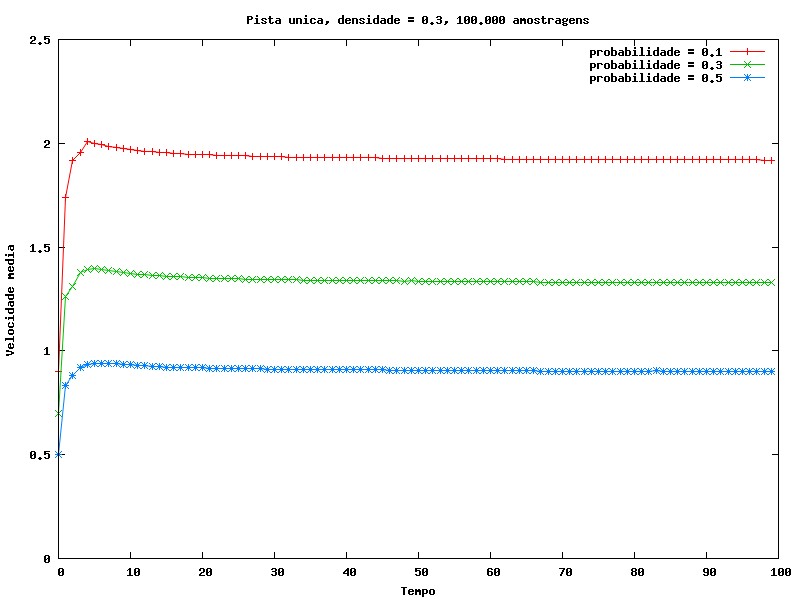
Podemos também analisar a influência da probabilidade de redução da velocidade na velocidade média em função do tempo. Como seria de se esperar, quanto menor essa probabilidade, maior a velocidade média de equilíbrio.
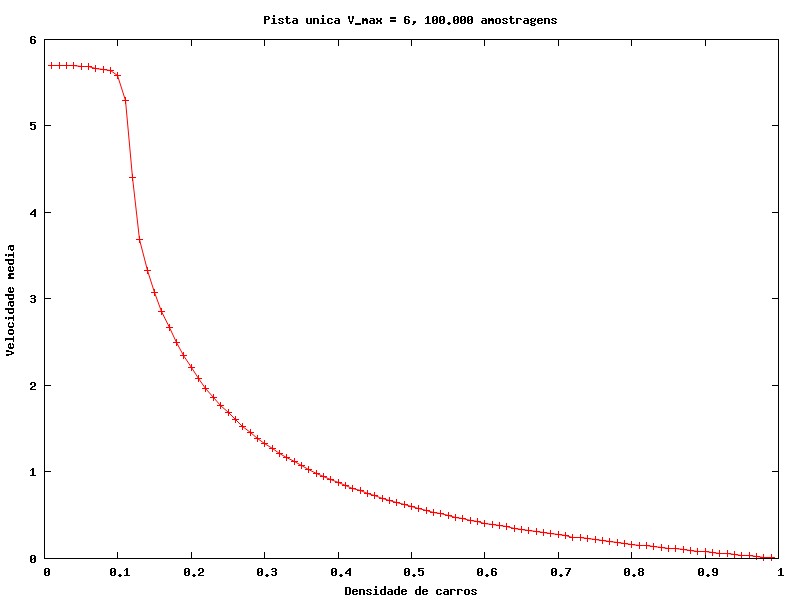
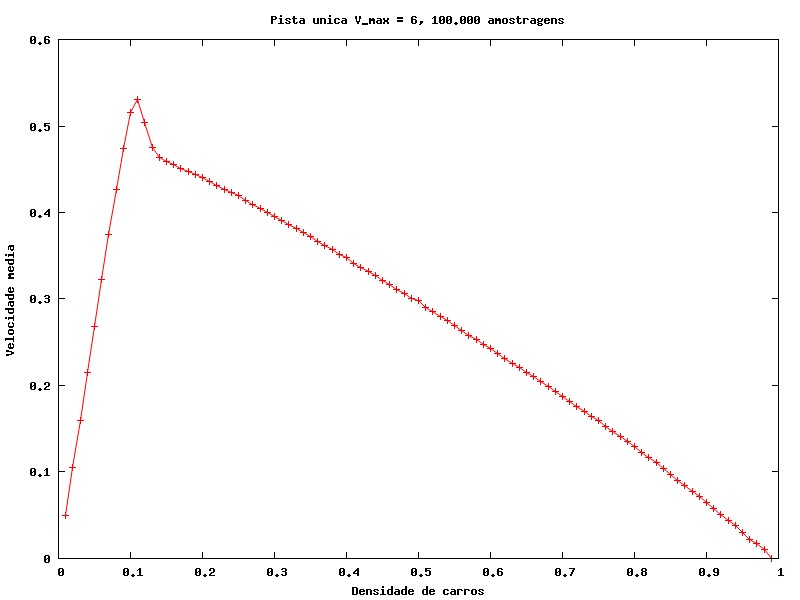
Outras medidas interessantes são a velocidade média em função da densidade de carros (número de carros/número de células) e o fluxo em função da densidade de carros. O fluxo é medido como o número de carros que atravessou a seção transversal da rua entre as posições 100 e 0 do vetor que descreve a rua (já que consideramos aqui condições de contorno periódicas) ao longo de toda a simulação, dividindo pelo tempo total. Os gráficos abaixo foram feitos a partir da média de 100000 amostragens.
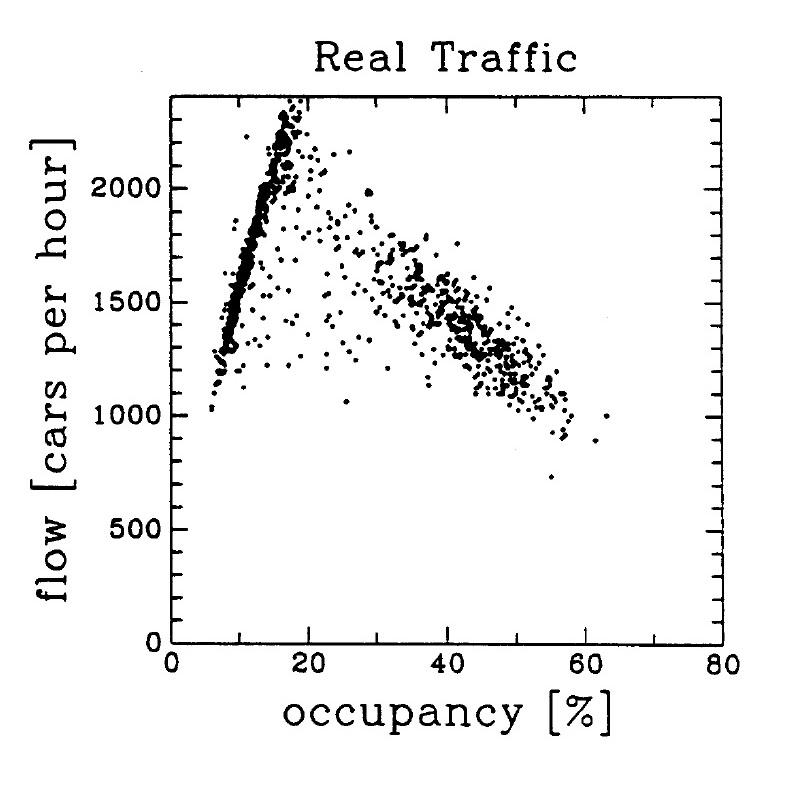
O gráfico 9 indica que, quanto maior a densidade, menor a velocidade média dos carros, o que é intuitivo. Também observamos que, para baixas densidades, a velocidade média se aproxima da velocidade máxima do sistema. O Gráfico 10 é mais interessante, indicando que existe uma densidade que maximiza o fluxo de carros: abaixo dela, o número baixo de veículos causa um pequeno fluxo; acima dela, a grande densidade faz com que a velocidade média seja pequena, diminuindo o fluxo de carros. Este gráfico é semelhante ao de uma situação real, conforme gráfico no artigo de Nagel e Schreckenberg[5], mostrado abaixo.
Faixa Dupla
É natural então, querermos simular o tráfego em uma pista com duas faixas, de mesmo sentido. Permitir que carros troquem faixa, à princípio, tornaria o sistema mais fluido.
Regras de Troca de Faixa
Surge então a necessidade de definir quando permitiremos que uma carro se mude para a faixa ao lado. Apenas definir uma probabilidade para tal evento não faz jus à realidade pois, mesmo que possível, a tendencia não é que pessoas troquem de faixa por motivo algum. Aqui foi utilizada a regra de que, ao reduzir a velocidade devido à falta de distância (ou seja, a regra 1), ou se o carro for obrigado a manter sua velocidade (ou seja, não se encaixar nem na regra 1 nem na regra 2), o motorista checa a faixa vizinha, medindo a distância ao próximo carro; se ela for maior do que a distância atual (medida a partir da faixa em que o carro se encontra), e se a faixa vizinha possuir espaço livre, a troca de pista ocorre. Na sequência, é refeito o processo de mudança de velocidade, levando em conta agora a nova pista em que o carro se encontra.
Simulações Iniciais
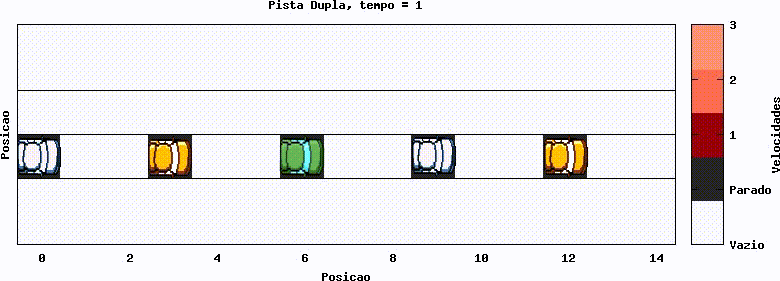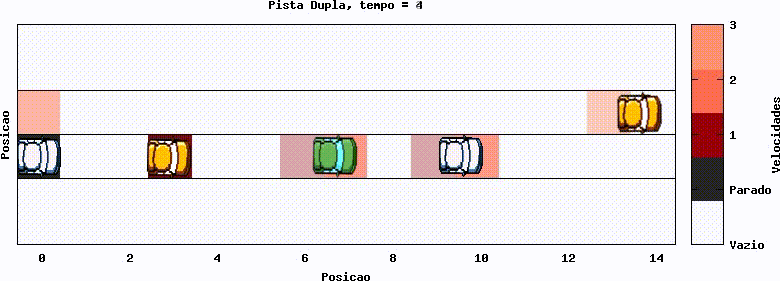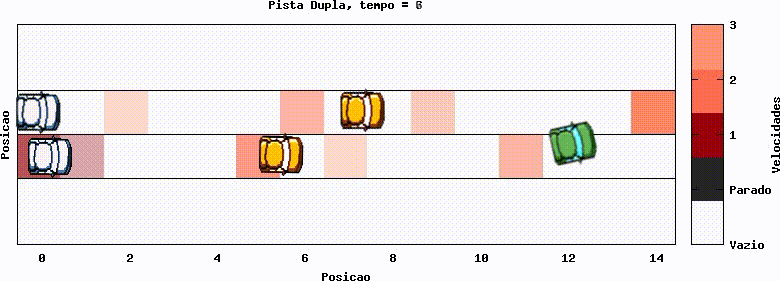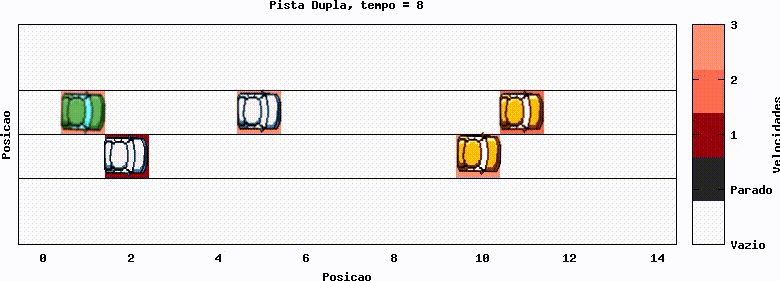
Os gráficos a seguir mostram implementações de faixa dupla. Nota-se, caso acompanhar um carro em específico, que ele troca de faixa quando necessário. Como exemplo, tome o carro que inicia na posição 12, no gráfico 12. Do tempo 2 ao 3 ele troca de faixa ao perceber que (lembrando das condições de contorno periódicas) há um carro bloqueando seu caminho.
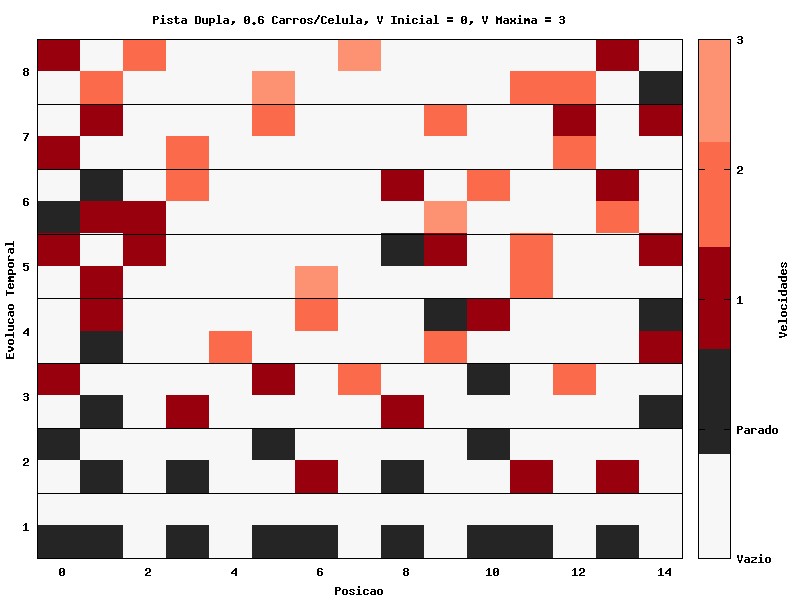
O mesmo pode ser feito com uma densidade de carros/celula maior.
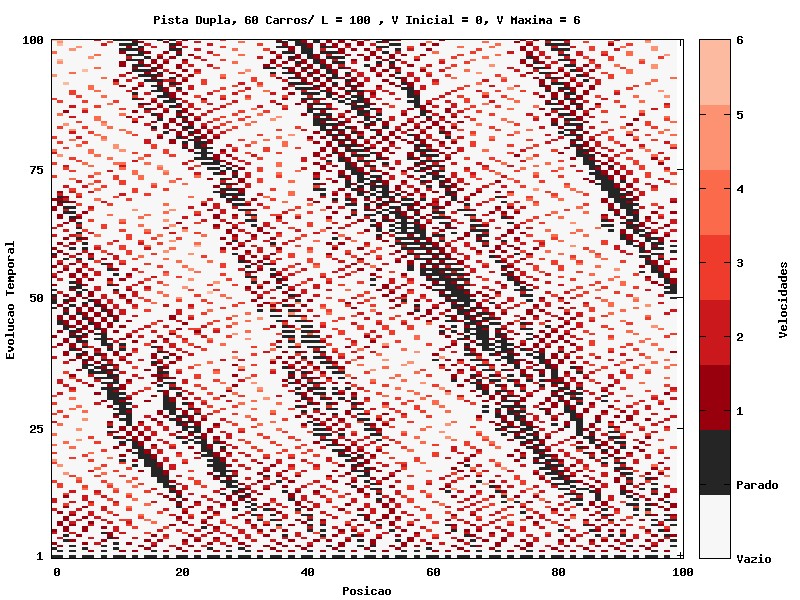
Comparado com o gráfico 5, o gráfico 14 mostra o resultado da duplicação de faixa. Temos um claro aumento na fluidez. Carros se ajeitam procurando a melhor configuração. Não deixa de gerar lentidão, até com trechos de congestionamento, mas a situação é bem melhor.
.
Medidas de Velocidade
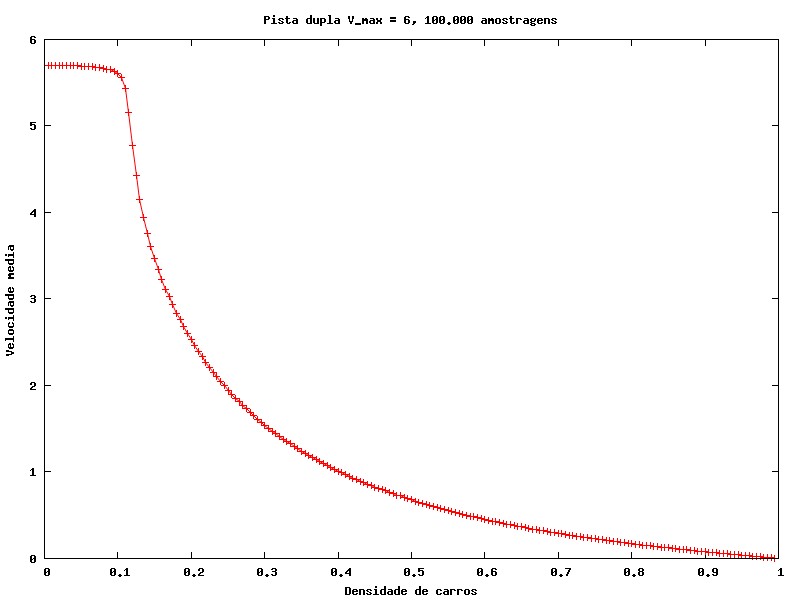
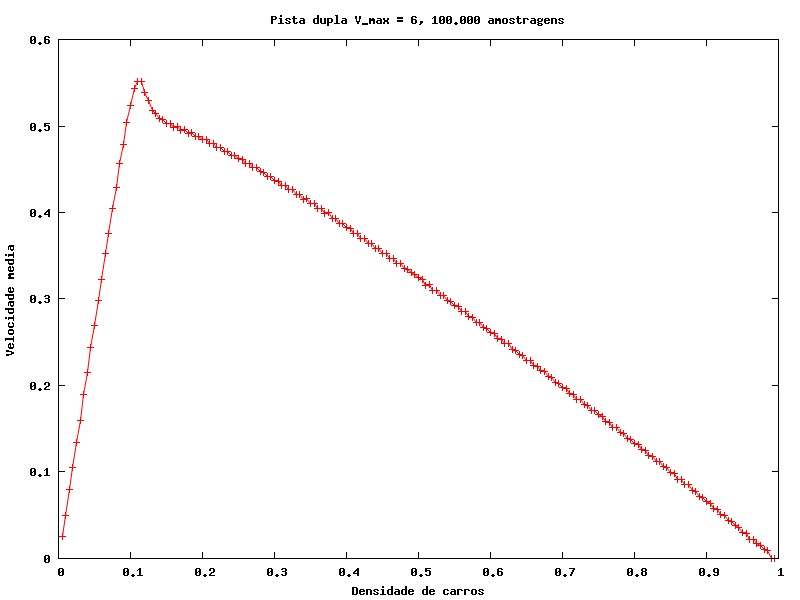
Da mesma forma que foi feita para pista única, podemos medir a velocidade média em função de diversos parâmetros. Os resultados são semelhantes aos obtidos anteriormente, mas têm uma diferença, que será explorada na próxima seção.
Também pode ser feito o mesmo estudo do fluxo e da velocidade média em função da densidade de carros, conforme os gráficos abaixo.
Comparação entre faixa simples e dupla
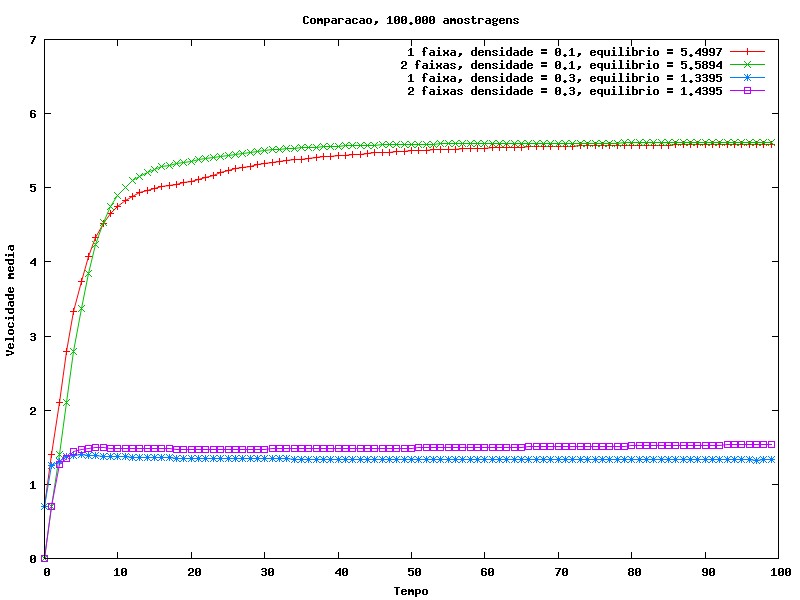
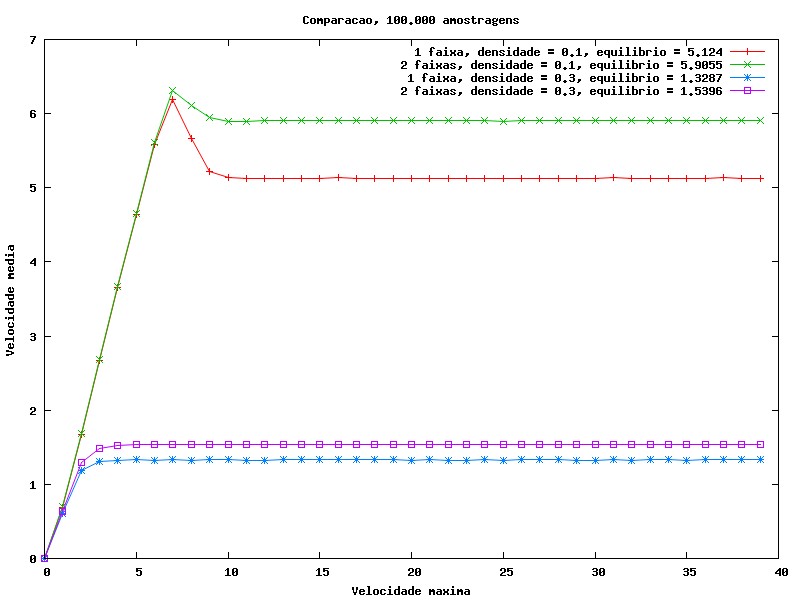
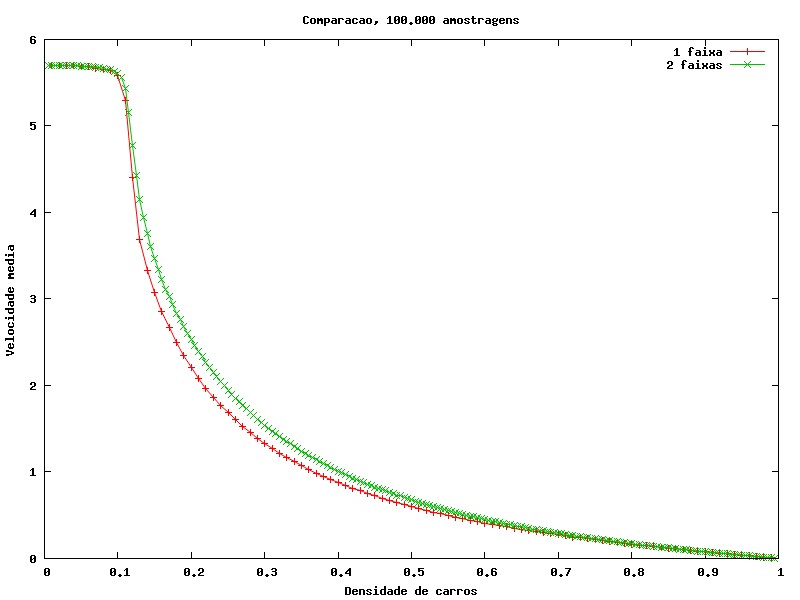
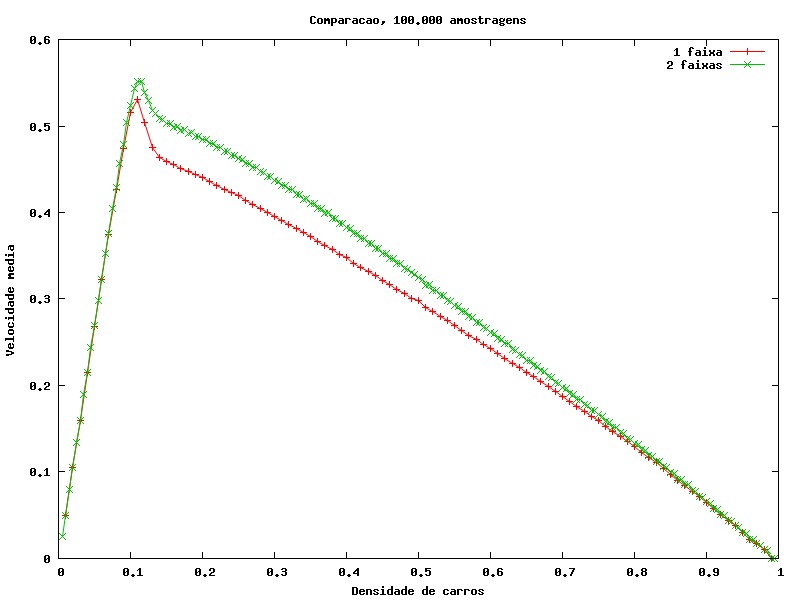
Após realizarmos essas medidas de velocidade média e fluxo de carros, é natural compararmos os resultados para pista simples e pista dupla. Abaixo, mostramos essas comparações, simplesmente unindo os gráficos para esses dois tipos de pista.
Através desses quatro gráficos, podemos observar claramente que uma rua com pista dupla é mais fluida do que uma de pista simples.
N faixas
O programa foi estendido para comportar uma simulação de faixas. Análises futuras podem, por exemplo, verificar a eficácia da adição de uma faixa à uma avenida, informação valiosa para coordenadores de trafego em uma cidade movimentada que buscam informações sobre custo/benefício de tal obra. Também é possível analisar os impactos da redução de uma faixa, ou do bloqueio de lugares pontuais, comparando diversas simulações.
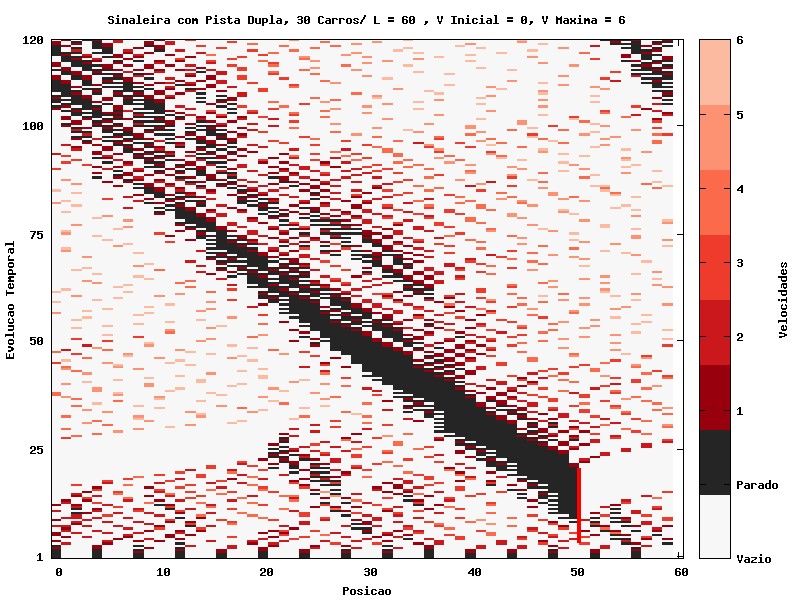
Sinaleira
Funcionamento
Códigos
Uma pista
Códigos em C
Velocidade média em função da velocidade máxima
Velocidade média em função do tempo
Velocidade média em função da densidade e fluxo em função da densidade
Códigos para Gnuplot
Gnuplot - Plot base Matrizes de dados
Gnuplot - Velocidade média em função da velocidade máxima
Gnuplot - Velocidade média em função do tempo
Gnuplot - Velocidade média em função da densidade e fluxo em função da densidade
Comparação entre diferentes probabilidades de redução de velocidade
N pistas
Códigos em C
N pistas: Velocidade média em função da velocidade máxima
N pistas: Velocidade média em função do tempo
N pistas: Velocidade média em função da densidade e fluxo em função da densidade
Códigos para Gnuplot
Gnuplot - N pistas: Velocidade média em função da velocidade máxima
Gnuplot - N pistas: Velocidade média em função do tempo
Gnuplot - N pistas: Velocidade média em função da densidade e fluxo em função da densidade
Comparação entre pista simples e dupla
Bibliografia
- ↑ http://transito.maplink.global/RS/porto_alegre/Estatisticas
- ↑ http://transito.maplink.global/SP/sao_paulo/Estatisticas
- ↑ Weimar, Jörg R. (1998). "Simulation with Cellular Automata". Berlin: Logos-Verlag.
- ↑ https://www.ppgee.ufmg.br/defesas/113M.PDF
- ↑ 5,0 5,1 5,2 Nagel, K.; Schreckenberg, M. (1992). A cellular automaton model for freeway traffic. J. Phys I France (2221-2229)