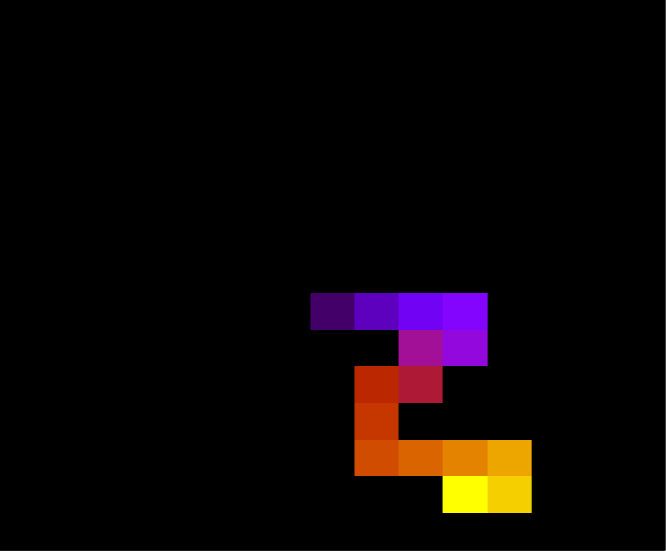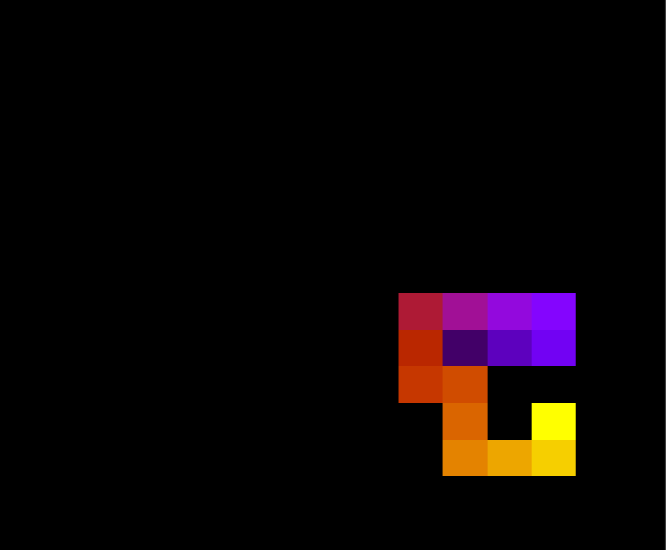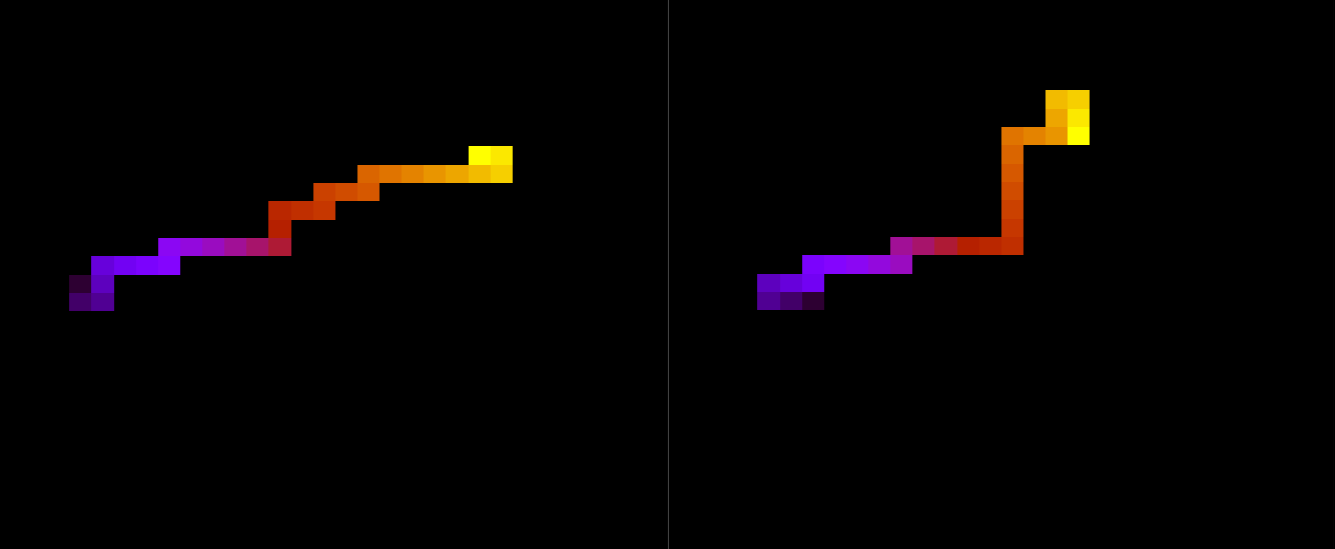Simulação de Enovelamento de Proteína
Carolina Lenzi
Este trabalho tem como objetivo utilizar o método de Monte Carlo para simular o enovelamento de proteínas.
Proteínas
As proteínas são macromoléculas com papel fundamental em diversos processos biológicos, como o transporte de oxigênio, a catálise de reações químicas, a defesa do organismo e a formação dos hormônios. Elas são formadas por centenas de aminoácidos ligados em cadeia por ligações covalentes. Existem 20 aminoácidos proteinogênicos conhecidos que dão origem às proteínas conhecidas na natureza. Cada sequência de aminoácidos ligados covalentemente gera uma proteína diferente, e essa sequência, bem determinada, é chamada de estrutura primária da proteína. A cadeia possui uma certa flexibilidade em suas ligações, que permite a movimentação dos aminoácidos no espaço. Devido à interações não covalentes (como ligações de hidrogênio, ponte salina, interações hidrofóbicas, interações iônicas…) entre os aminoácidos e com o meio, as proteínas tendem a se enovelar, gerando regiões com padrões regulares na macromolécula, chamadas de estrutura secundária da proteína. Essas regiões regulares também tendem a se enovelar, dando origem a estrutura terciária da proteína. As estruturas terciárias são, geralmente, a conformação funcional da proteína, ou seja, sua configuração em estado biologicamente ativo, que é conhecida como conformação nativa.
O enovelamento é uma estratégia de minimização da energia e leva sempre à mesma estrutura: a forma nativa da proteína. Existem muitas estruturas terciárias possíveis para a mesma cadeia de aminoácidos, pois as ligações covalentes permitem a rotação da molécula. Se considerarmos, por exemplo, que os aminoácidos tem 3 conformações possíveis, o que é uma estimativa baixa, para uma cadeia com 100 aminoácidos, existem possibilidades de estrutura terciária. Se levasse 10-13s para testar cada configuração, o tempo necessário para testar todas seria 1027 anos (quase 3 vezes a idade do universo!). Entretanto, as proteínas atingem a forma nativa em fração de segundo… essa divergência é conhecida como paradoxo de Levinthal.
Simulação de Monte Carlo
A simulação do enovelamento foi feita com base no livro do Giordano e envolve um modelo muito simplificado do que acontece na realidade. O código foi implementado em C e os gráficos foram gerados no gnuplot.
Consideramos uma cadeia de N aminoácidos, sorteados dentre os 20 possíveis, para montar a estrutura primária da proteína, representada por um vetor de tamanho N. Aminoácidos em posições adjacentes do vetor são considerados ligados covalentemente. A cadeia é colocada em uma rede quadrada de tamanho NxN, para permitir que a proteína esteja completamente desenovelada (esticada). Em cada posição da rede, um aminoácido tem no máximo 4 aminoácidos vizinhos mais próximos com os quais pode interagir ou estar ligado, sendo eles acima, abaixo, à direita e à esquerda. Para as interações de estabilização da proteína, consideramos as seguintes forças atuantes:
- Forças de van der Waals entre aminoácidos não ligados covalentemente: força atrativa para aminoácidos próximos, que perde o efeito com o aumento da distancia entre os aminoacidos;
- Ligações de hidrogênio: ligações entre aminoácidos próximos na rede;
- Interação com a água (hidrofilicidade e hidrofobia): aminoácidos hidrofílicos são atraídos pela água presente no meio e, por isso, tendem a manter a cadeia não enovelada. Já os hidrofóbicos repelem a água do meio e preferem uma estrutura enovelada.
Todas essas forças estão competindo no processo de enovelamento da proteína. Para o modelo, agrupamos essas interações em uma energia , associada a um par de aminoácidos vizinhos na rede, A(m) e A(n) nas posições i e j, e não ligados covalentemente, ou seja, não adjacentes na cadeia. A energia da estrutura é dada pela soma sobre todos os pares de aminoácidos da proteína:
onde se os aminoácidos m e n são vizinhos na rede e não estão ligados covalentemente, e zero caso contrário.
No livro, os autores sugerem pensar as energias como uma matriz 20x20 contendo todas as interações entre os 20 aminoácidos considerados. Porém, como a interação depende apenas de quais são os aminoácidos do par, a matriz é simétrica , e podemos guardar apenas 210 valores correspondentes aos pares distintos de aminoácidos.
Com essas definições, podemos partir para a simulação de Monte Carlo. Inicialmente, sorteamos um aminoácido e encontramos a posição dele na rede. Cada posição tem no máximo 8 vizinhos para onde o aminoácido pode (ou não) ser movido, que são os 4 vizinhos mais próximos e as diagonais para cima e para baixo. Calculamos a energia inicial da estrutura e partimos para a tentativa de movimento: sorteamos um de seus vizinhos e analisamos se é possível mover o aminoácido. Primeiro, verificamos se a rede está vazia na posição do vizinho sorteado e, em caso positivo, verificamos se nenhuma ligação entre aminoácidos será comprimida ou esticada com o movimento. Se essas duas condições forem satisfeitas, realizamos o movimento e calculamos a energia final da estrutura. Se a energia final for menor que a inicial, aceitamos o movimento e voltamos ao primeiro passo. Se a energia final for maior que a inicial, aceitamos o movimento apenas se o fator de Boltzmann for maior que um valor aleatório entre 0 e 1. Caso o movimento não seja aceito, recuperamos a estrutura inicial da proteína. Repetimos esses passos diversas vezes e, a cada tentativa de movimento, contamos um tempo de Monte Carlo.
Resultados
Em todas as simulações, a posição inicial da cadeia foi esticada horizontalmente no meio da matriz da rede. Os valores de foram sorteados dentro do intervalo [-4, -2], como utilizado no livro. As energias foram medidas em unidades de kB por simplicidade.
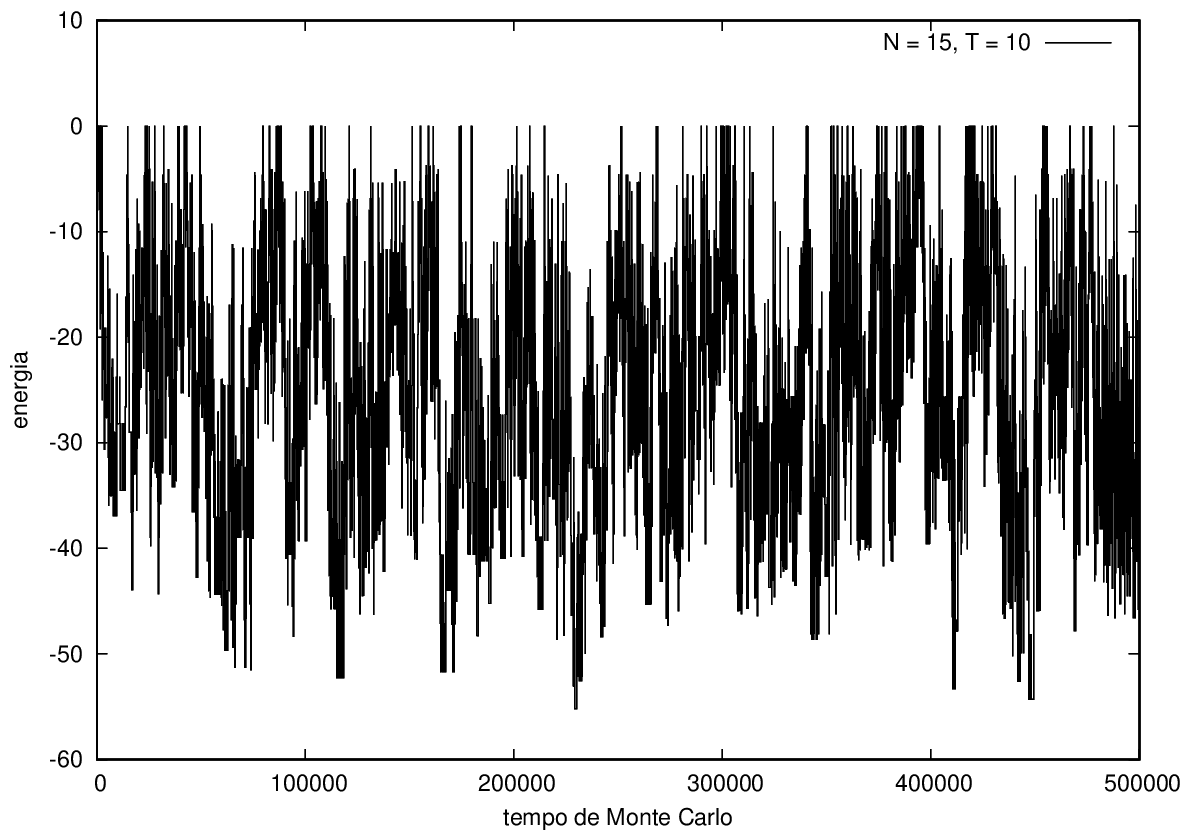
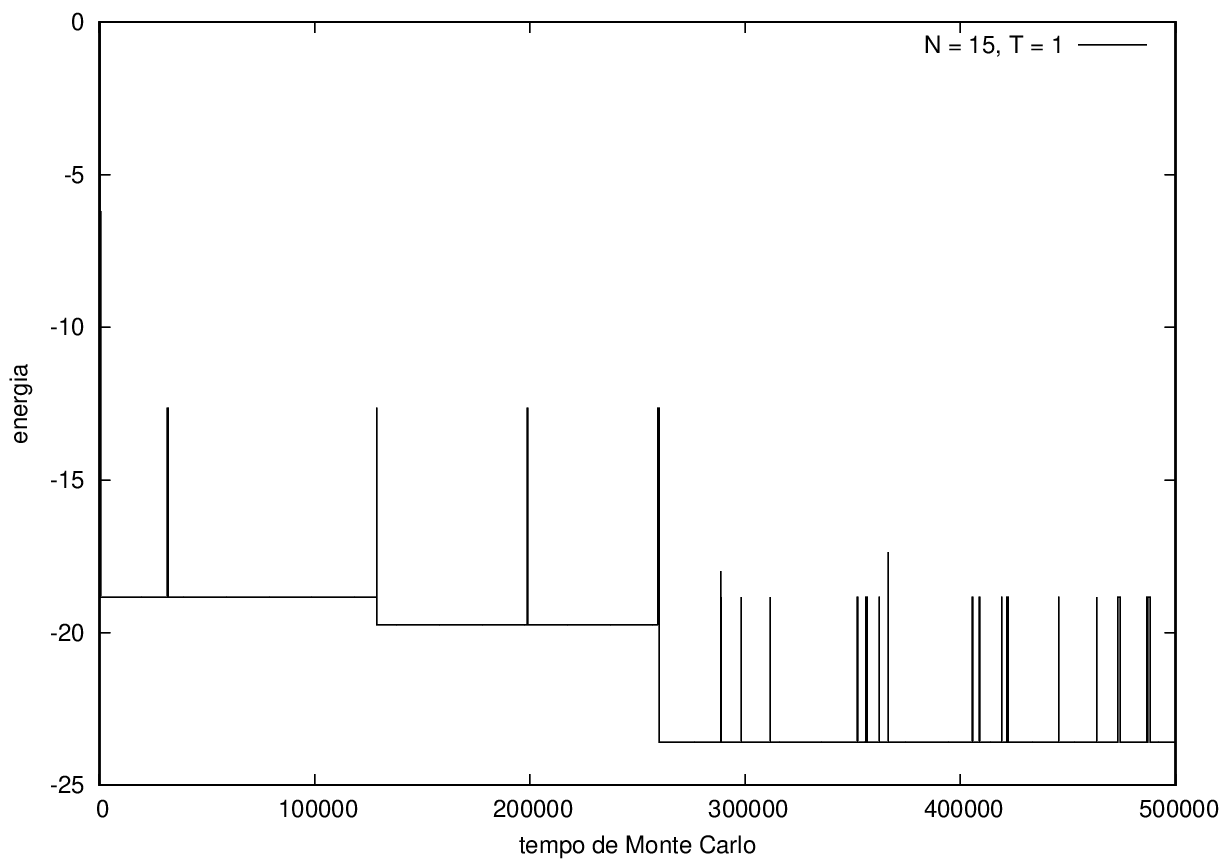
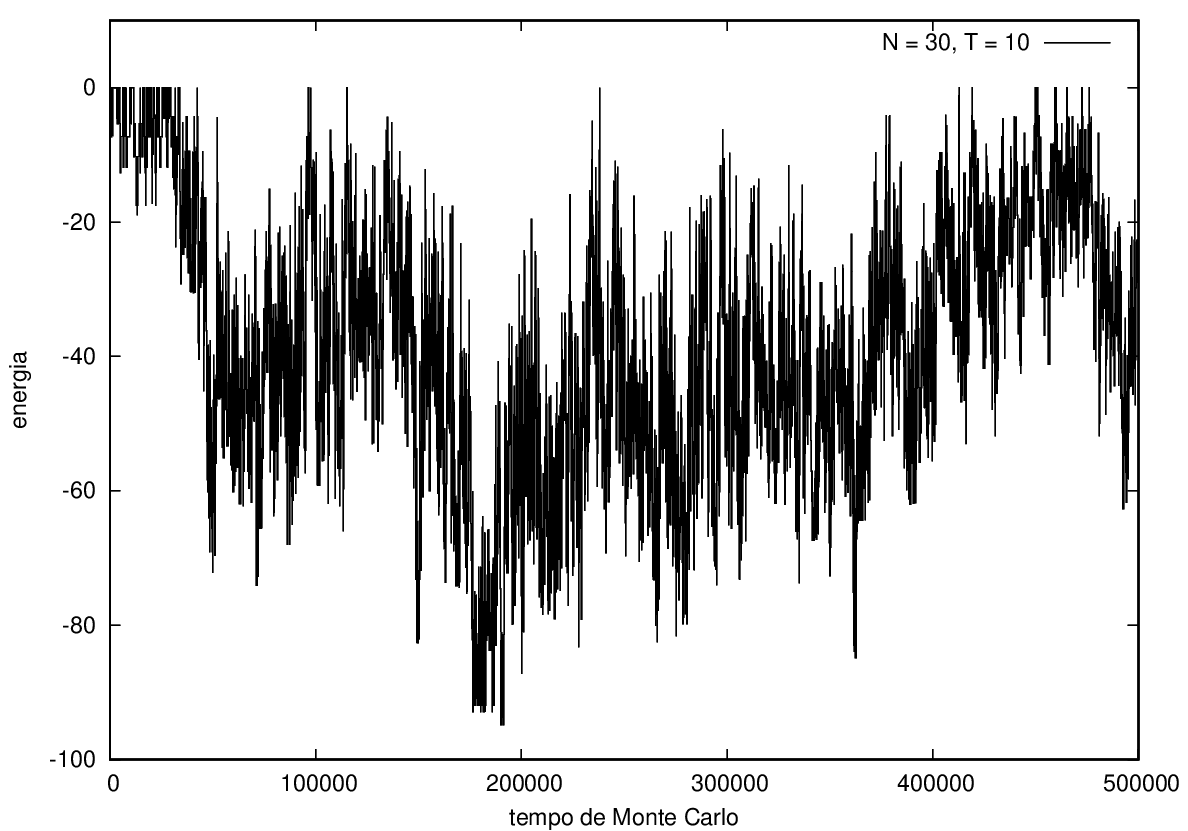
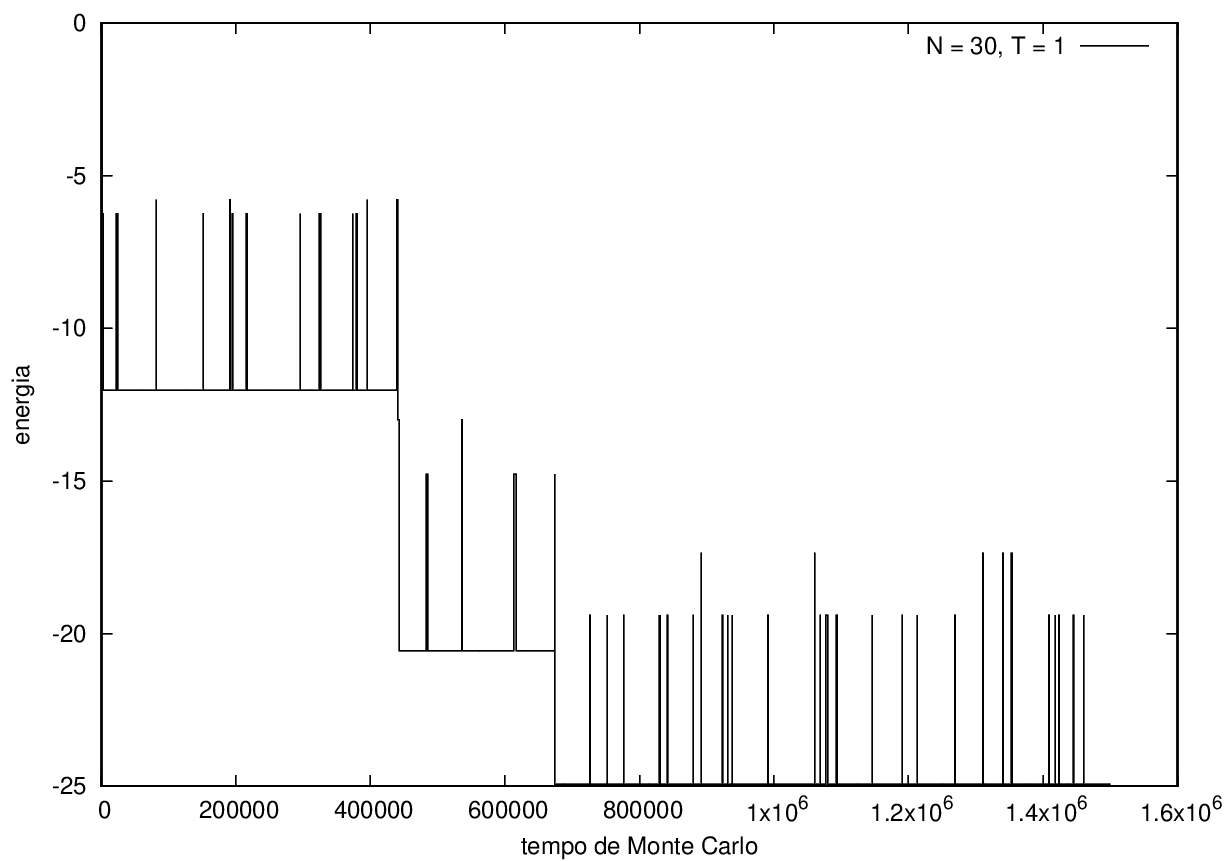
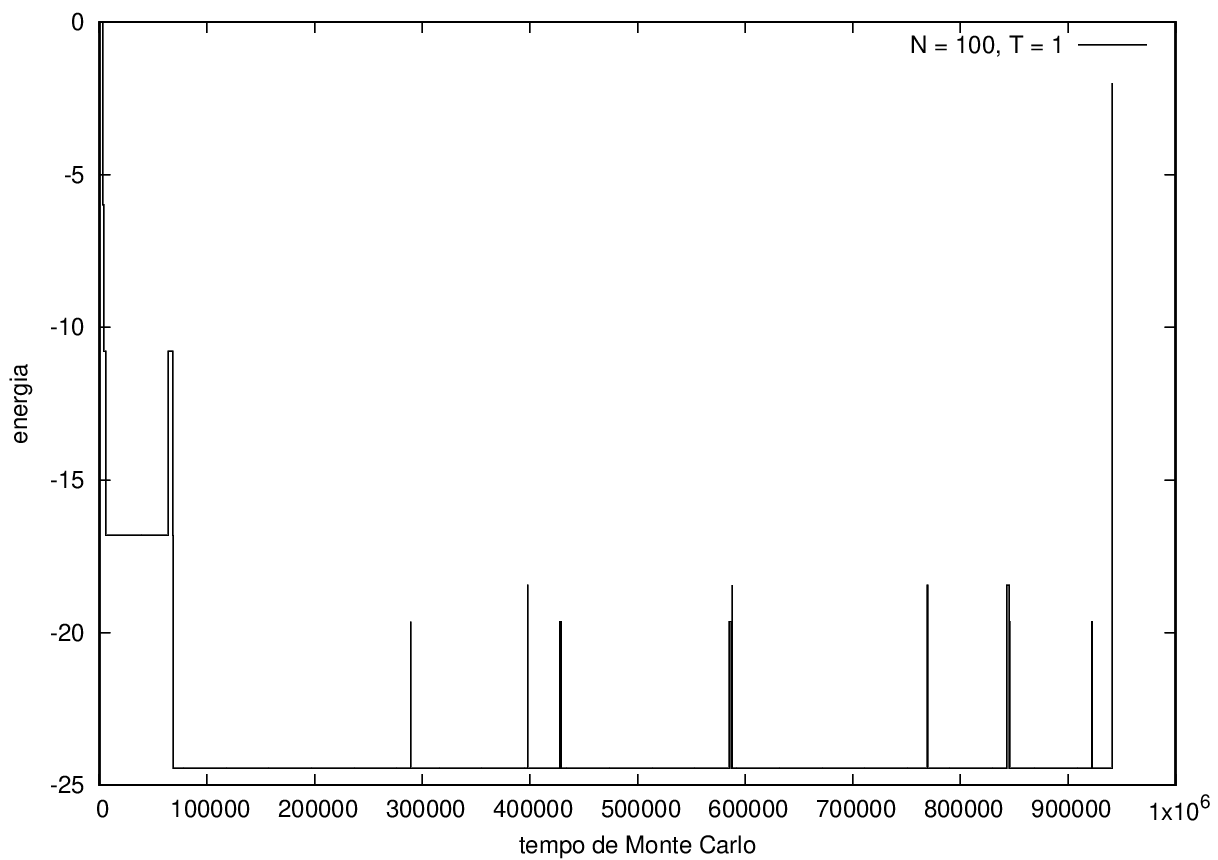
Na figura 1, observamos o gráfico da energia em função do tempo durante a simulação para uma proteína com 15 aminoácidos à temperatura T = 10. As flutuações de energia são grandes pois a temperatura é alta, o que aumenta a probabilidade de alterar a estrutura da proteína. Já na figura 2, temos também a energia em função do tempo para uma proteína com 15 aminoácidos, mas à temperatura T = 1. Nesse caso, as flutuações diminuem consideravelmente e a proteína passa a maior parte do tempo em estados de menor energia.
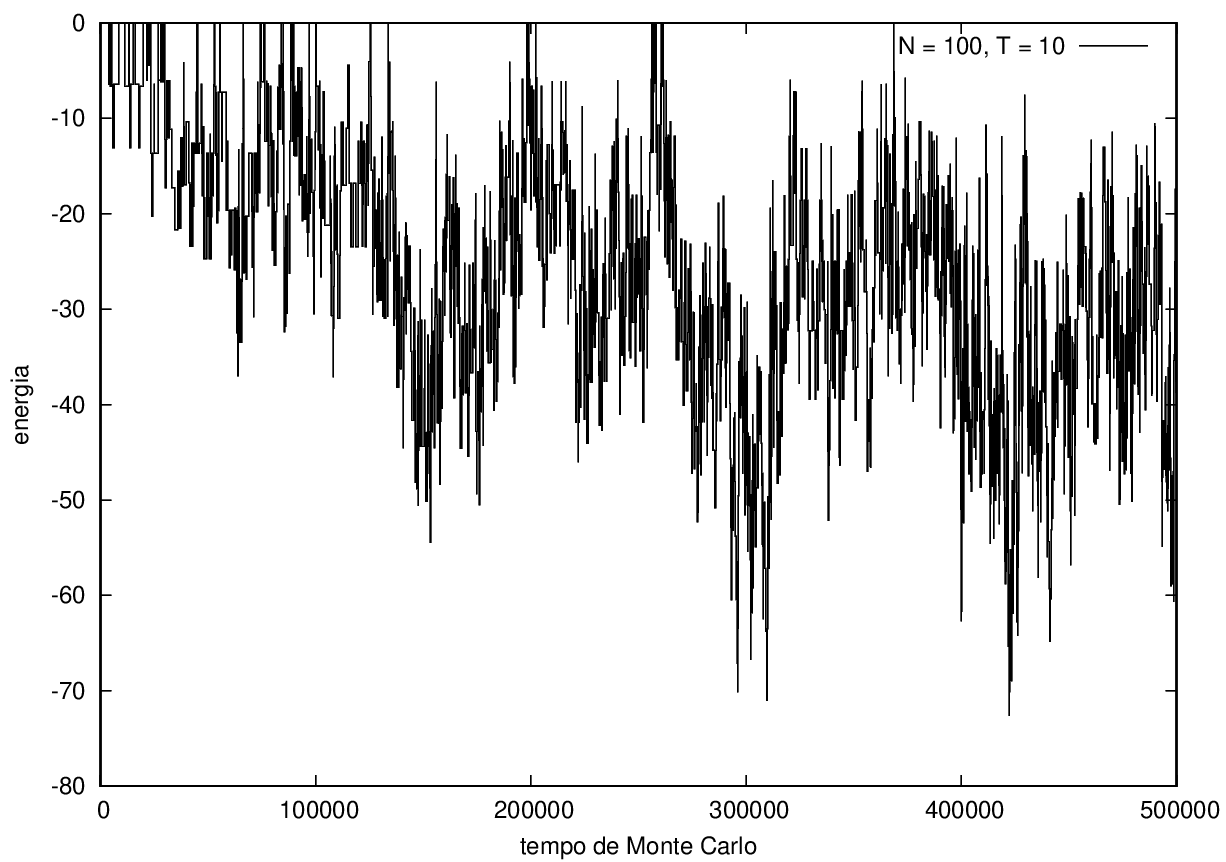
Nas figuras a seguir, a mesma comparação anterior, mas para o caso de proteínas com 30 (figuras 3 e 4) e com 100 (figuras 5 e 6) aminoácidos.
Abaixo, duas configurações da mesma proteína com 30 aminoácidos durante a simulação, para T = 1.




![{\displaystyle J[A(m),A(n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85b9ebc5fd30f75da1c35033a8ffd7ceb2bc93d5)
![{\displaystyle \left(J[A(m),A(n)]=J[A(n),A(m)]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2999c491c5aca3b48e7fa20c48c6dc5a3a2bc591)