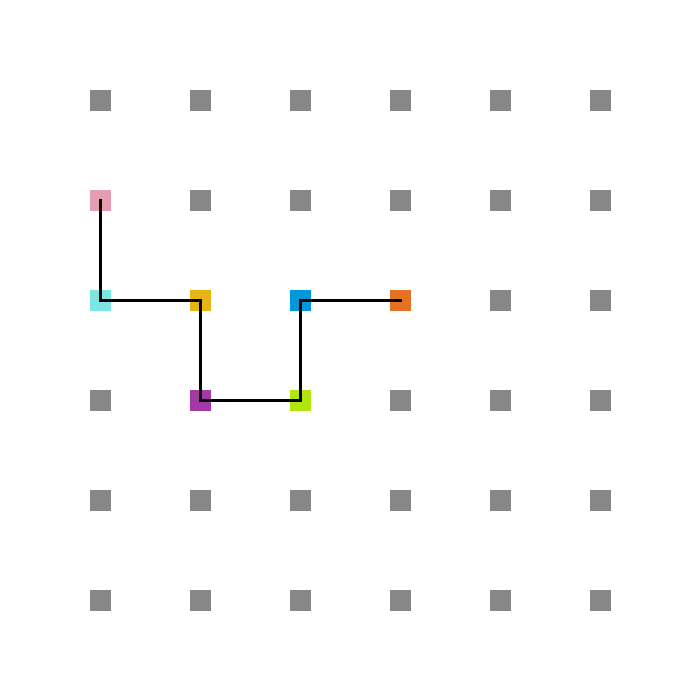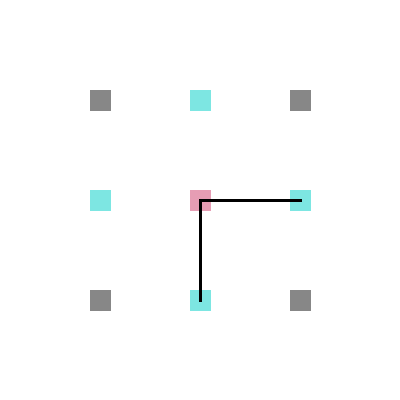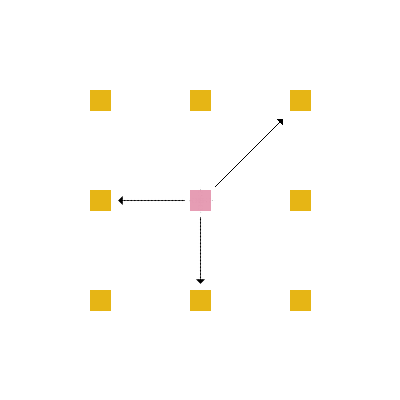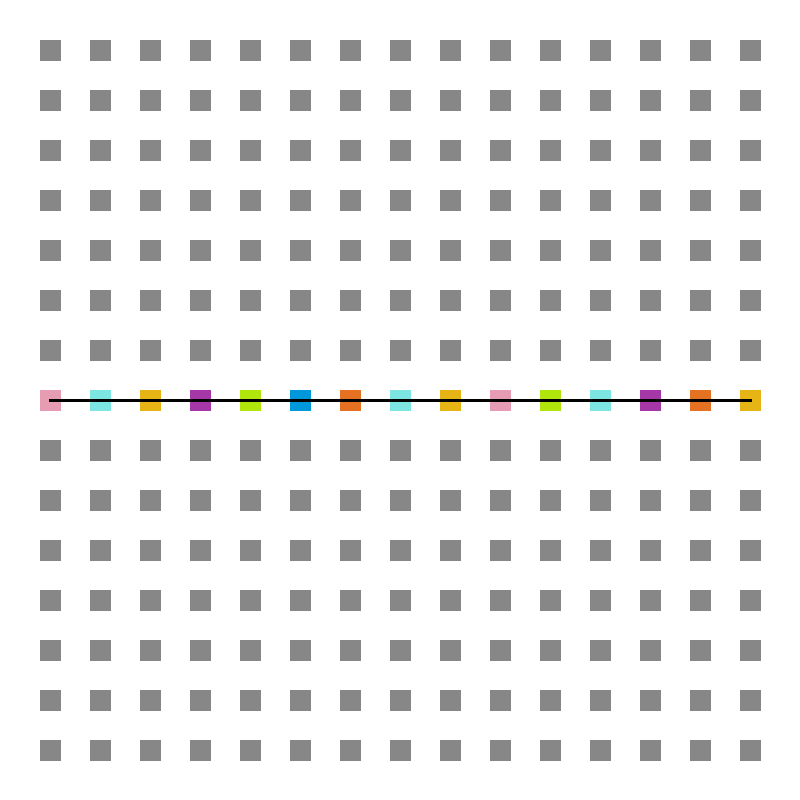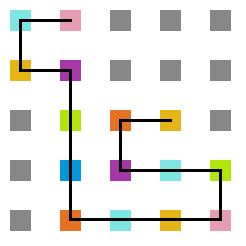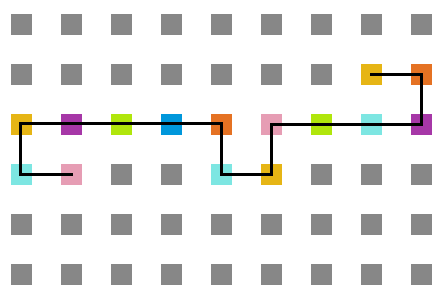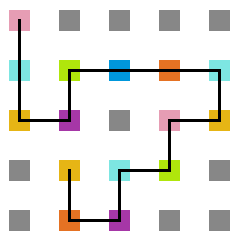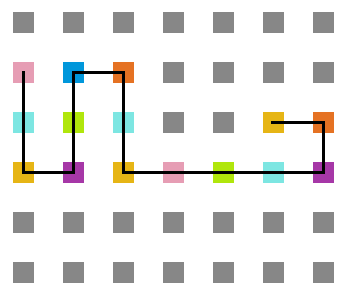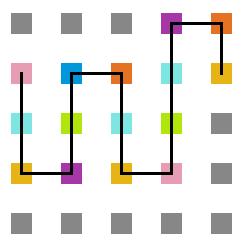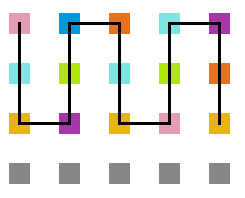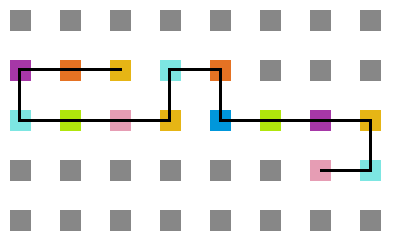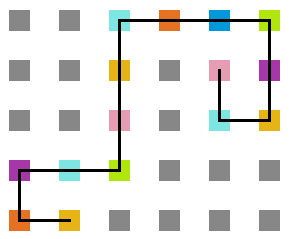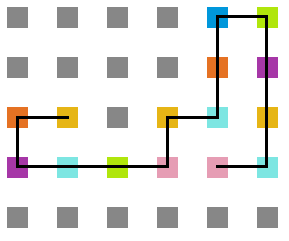Simulação de Enovelamento de Proteína: mudanças entre as edições
| (36 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 3: | Linha 3: | ||
Este trabalho tem como objetivo utilizar o método de Monte Carlo para simular o enovelamento de proteínas. | Este trabalho tem como objetivo utilizar o método de Monte Carlo para simular o enovelamento de proteínas. | ||
== Proteínas == | |||
As proteínas são moléculas com papel fundamental para os seres vivos. Elas atuam em diversos processos biológicos, como o transporte de oxigênio, a catálise de reações químicas, a defesa do organismo, a formação dos hormônios e formação de ossos e tendões. As proteínas são formadas por centenas de aminoácidos ligados em cadeia por ligações covalentes. Existem 20 aminoácidos proteinogênicos que dão origem às proteínas conhecidas e encontradas na natureza. Cada sequência de aminoácidos ligados covalentemente gera uma proteína diferente, com uma função específica no organismo. Essa sequência, bem determinada, é chamada de estrutura primária da proteína. | |||
[[Arquivo:Estruturas.png|400px|thumb|right|'''Figura 1''': Estruturas da proteína]] | |||
A proteína tende a se enovelar para minimizar a energia da sua estrutura, relativa às interações não covalentes (como ligações de hidrogênio, ponte salina, interações hidrofóbicas, interações iônicas…) entre os aminoácidos e com o meio. Isso é possível porque as ligações químicas possuem uma certa flexibilidade, que permite a rotação das moléculas. O enovelamento da estrutura primária gera regiões com padrões regulares na proteína, chamadas de estrutura secundária. Essas regiões regulares também tendem a se enovelar, dando origem a estrutura terciária da proteína. A estrutura terciária de menor energia é, geralmente, a conformação funcional da proteína, ou seja, sua configuração em estado biologicamente ativo, que é conhecida como forma nativa. Em alguns casos as estruturas terciárias podem se aglomerar e formar as estruturas quaternárias. | |||
Como a função da proteína está diretamente relacionada com a sua forma nativa, e esta está relacionada com a sequência de aminoácidos que dá origem à proteína, é interessante conseguir prever a estrutura terciária a partir da estrutura primária, com a finalidade de desenvolver proteínas com características específicas. Esse é um dos grandes problemas da bioinformática atualmente. Além da complexidade de compreender a termodinâmica e o mecanismo do enovelamento, a proteína encontra a estrutura ótima em fração de segundo, mas o tempo que seria necessário para testar aleatoriamente as estruturas possíveis para encontrar a de menor energia é maior que a idade do universo, como apontado no paradoxo de Levinthal. | |||
== Simulação de Monte Carlo == | == Simulação de Monte Carlo == | ||
A simulação do enovelamento foi feita com base no livro do Giordano e envolve um modelo muito simplificado do que acontece na realidade. | A simulação do enovelamento foi feita com base no livro do Giordano e envolve um modelo muito simplificado do que acontece na realidade. | ||
Consideramos uma cadeia de N aminoácidos, sorteados dentre os 20 possíveis, para montar a estrutura primária da proteína, representada por um vetor de tamanho N. Aminoácidos em posições adjacentes do vetor são considerados ligados covalentemente. A cadeia é colocada em uma rede quadrada de tamanho NxN, para permitir que a proteína esteja completamente desenovelada (esticada). | |||
[[Arquivo:Cadeia0N.png|300px|thumb|right|'''Figura 2''': Cadeia de N aminoácidos]] | |||
[[Arquivo:Rede.png|300px|thumb|right|'''Figura 3''': Rede NxN]] | |||
*Forças de van der Waals | Em cada posição da rede, um aminoácido tem no máximo 4 aminoácidos vizinhos mais próximos com os quais pode interagir ou estar ligado (figura 4) e no máximo 8 posições vizinhas para as quais ele pode se mover (figura 5). | ||
<gallery widths=200px heights=200px> | |||
Arquivo:4v.png|'''Figura 4''': Interação e ligação | |||
Arquivo:8v.png|'''Figura 5''': Movimentação | |||
</gallery> | |||
Para as interações de não covalentes entre os aminoácidos, consideramos as seguintes forças atuantes: | |||
*Forças de van der Waals: força atrativa para aminoácidos próximos, que perde o efeito com o aumento da distancia entre os aminoacidos; | |||
*Ligações de hidrogênio: ligações entre aminoácidos próximos na rede; | *Ligações de hidrogênio: ligações entre aminoácidos próximos na rede; | ||
*Interação com a água (hidrofilicidade e hidrofobia): aminoácidos hidrofílicos são atraídos pela água presente no meio e, por isso, tendem a manter a cadeia não enovelada. Já os hidrofóbicos repelem a água do meio e preferem uma estrutura enovelada. | *Interação com a água (hidrofilicidade e hidrofobia): aminoácidos hidrofílicos são atraídos pela água presente no meio e, por isso, tendem a manter a cadeia não enovelada. Já os hidrofóbicos repelem a água do meio e preferem uma estrutura enovelada. | ||
Todas essas forças estão competindo no processo de enovelamento da proteína. Para o modelo, agrupamos essas interações em uma energia < | Todas essas forças estão competindo no processo de enovelamento da proteína. Para o modelo, agrupamos essas interações em uma energia J<sub>ij</sub>, associada a um par de aminoácidos vizinhos na rede, A(m) e A(n) nas posições i e j, e não ligados covalentemente, ou seja, não adjacentes na cadeia. A energia da estrutura é dada pela soma sobre todos os pares de aminoácidos da proteína: | ||
:<math> E = \sum_{<m,n>}\delta_{m,n}J_{A(m), A(n)}</math> | :<math> E = \sum_{<m,n>}\delta_{m,n}J_{A(m), A(n)}</math> | ||
| Linha 26: | Linha 42: | ||
onde <math>\delta_{m, n} = 1</math> se os aminoácidos m e n são vizinhos na rede e não estão ligados covalentemente, e zero caso contrário. | onde <math>\delta_{m, n} = 1</math> se os aminoácidos m e n são vizinhos na rede e não estão ligados covalentemente, e zero caso contrário. | ||
A energia J pode ser pensada como uma matriz 20x20 contendo as interações relativas a todos os pares de aminoácidos, porém a matriz é simétrica, portanto, podemos guardar apenas 210 valores correspondentes aos pares distintos de aminoácidos. | |||
Com essas definições, podemos partir para a simulação de Monte Carlo. | Com essas definições, podemos partir para a simulação de Monte Carlo, esquematizada a seguir. O código foi implementado em C, e se encontra no [https://github.com/carollenzi/montecarlo_enovelamento.git Github] | ||
# Inicializar a cadeia e posicionar na rede | |||
# Sortear um aminoácido da cadeia e encontrar sua posição na rede | |||
# Calcular a energia inicial (Ei) da estrutura | |||
# Sortear um dos 8 vizinhos da posição do aminoácido | |||
# Verificar se é possível mover o aminoácido para a posição vizinha sorteada | |||
## Se possível, mover o aminoácido e calcular a energia da nova estrutura (Ef) | |||
## Se Ef < Ei, aceitar o movimento | |||
## Se Ef >= Ei, aceitar o movimento com probabilidade do fator de Boltzmann <math>\left(e^{-\frac{\Delta E}{k_BT}}\right)</math> | |||
## Desfazer o movimento se ele não for aceito | |||
# Contar um tempo de Monte Carlo a cada sorteio de vizinho | |||
# Repetir a partir do passo 2. | |||
A simulação consiste em repetir esses passos (a partir do 2) por longos tempos de Monte Carlo. | |||
== Resultados == | == Resultados == | ||
Em todas as simulações, foi utilizada a mesma cadeia de 15 aminoácidos e os mesmos valores de energia J<sub>ij</sub>, que foram sorteados dentro do intervalo [-4, -2]. As energias foram medidas em unidades de k<sub>B</sub> por simplicidade. Incicialmente, a cadeia foi colocada esticada no meio da rede, como mostra a figura 6. Os gráficos foram gerados no gnuplot e as figuras da rede e das estruturas foram feitas no GIMP. | |||
Em todas as simulações, a | |||
'''OBS''': não foram utilizadas condições de contorno periódicas. | |||
[[Arquivo:Redeini.png|300px|thumb|right|'''Figura 6''': Rede inicial]] | |||
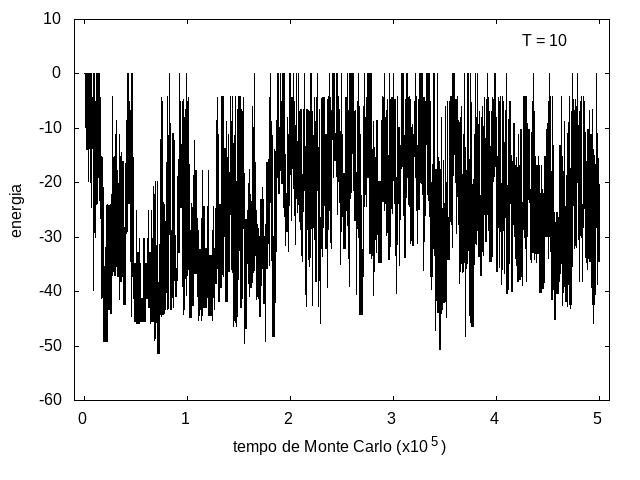
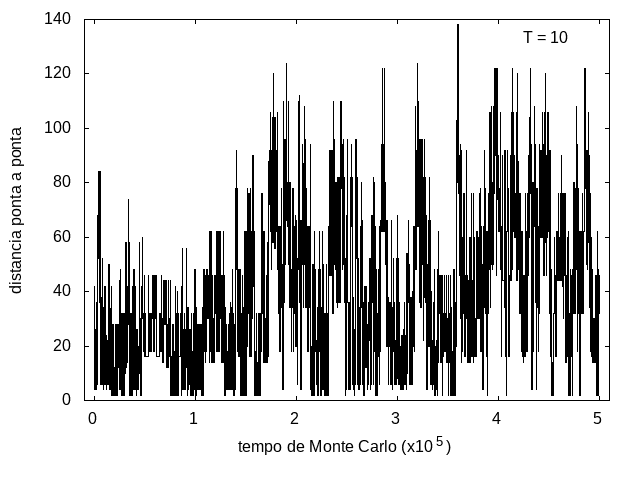
Nas figuras a seguir, temos a energia e o tamanho da cadeia (calculado como a distância ponta a ponta da cadeia) em função do tempo de simulação. Essa simulação foi feita com temperatura T = 10 e um total de 5x10<sup>5</sup> tempo de Monte Carlo. A temperatura alta permite que a proteína explore várias configurações e teste estruturas de diferentes energias, por isso, o gráfico tem tanta flutuação. Como várias estruturas diferentes são testadas, algumas são mais abertas e outras mais compactas, então o tamanho da cadeia também flutua bastante. | |||
<gallery widths=500px heights=500px> | |||
Arquivo:EnergiaT10.png|'''Figura 7''': Energia em função do tempo, T = 10 | |||
Arquivo:TamanhoT10.png|'''Figura 8''': Tamanho da cadeia em função do tempo, T = 10 | |||
</gallery> | |||
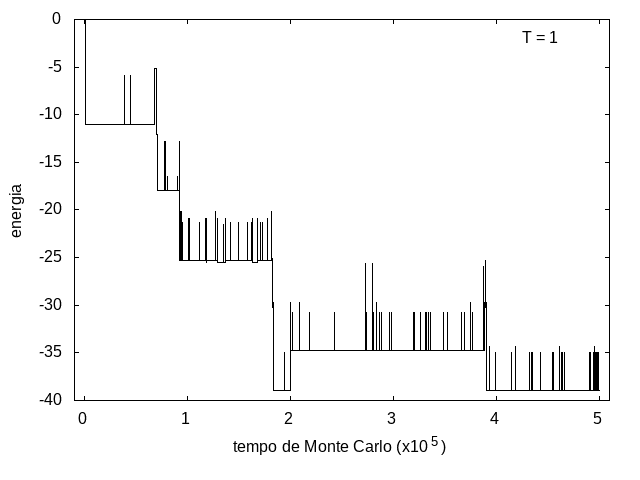
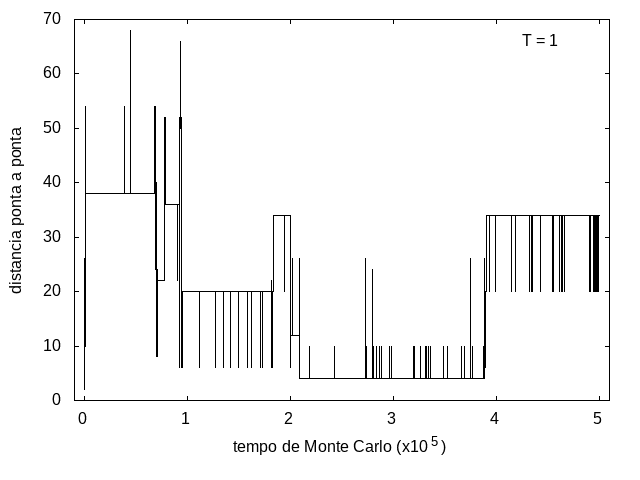
A simulação também foi feita para a temperatura T = 1, com o mesmo tempo de 5x10<sup>5</sup> tempo de Monte Carlo, e o resultado está nas figuras abaixo. As flutuações são menores e a proteína passa mais tempo em estruturas com energias mais baixas, porque a baixa temperatura não permite tanta movimentação. O tamanho também varia menos, e a proteína fica em estruturas mais compactas. | |||
<gallery widths=500px heights=500px> | |||
Arquivo:EnergiaT1.png|'''Figura 9''': Energia em função do tempo, T = 1 | |||
Arquivo:TamanhoT1.png|'''Figura 10''': Tamanho da cadeia em função do tempo, T = 1 | |||
</gallery> | |||
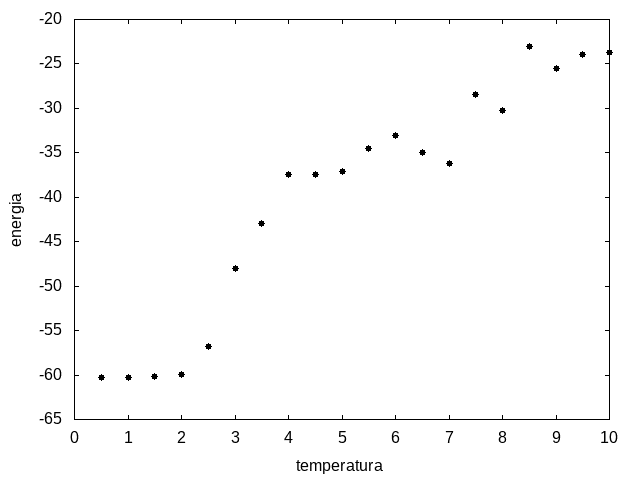
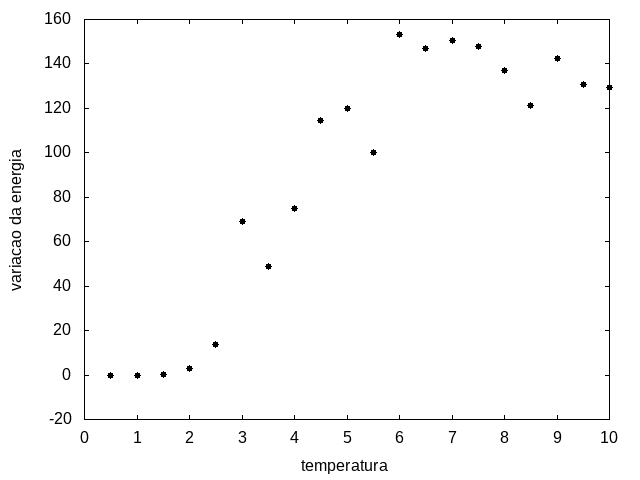
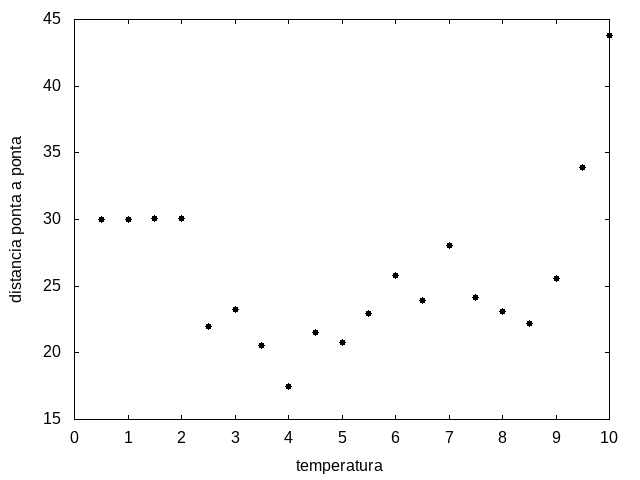
Outra simulação foi realizada partindo de uma temperatura alta e reduzindo-a gradativamente, para permitir que a proteína explore várias configurações nas temperaturas mais altas e consiga escolher uma de energia mais baixa. Em cada temperatura, a proteína passou 20x10<sup>5</sup> tempo de Monte Carlo. Os resultados, apresentados a seguir, são da média da energia e do tamanho em cada temperatura, e também a variância da energia em função da temperatura. | |||
<gallery widths=500px heights=500px> | |||
Arquivo:Energiaxtemp.png|'''Figura 11''': Média da energia em função da temperatura | |||
Arquivo:Variacaoxtemp.png|'''Figura 12''': Variação da energia em função da temperatura | |||
Arquivo:Tamanhoxtemp.png|'''Figura 13''': Média do tamanho da cadeia em função da temperatura | |||
</gallery> | |||
Percebemos, pelas figuras 11 e 12, que a energia da estrutura da proteína diminui com a temperatura, até T = 2, aproximadamente, onde não há mais uma mudança perceptível na energia. Isso indica que a proteína encontrou uma estrutura estável com energia baixa. A figura 13 também mostra estabilidade para temperaturas abaixo de 2, indicando que o estado enovelado da proteína não sofre alteração. Nesse caso, a estrutura encontrada pela proteína não é a mais compacta, mas é a de menor energia, dentre as testadas. '''OBS''': O resultado para o tamanho em função da temperatura não era o esperado, a curva deveria seguir a mesma tendência do gráfico da energia. Falta analisar o porquê disso. | |||
A seguir, algumas estruturas testadas pela proteína durante as simulações. | |||
<gallery widths=200px heights=200px caption="Simulação com T = 10" class="center"> | |||
Arquivo:T10_1e5.png|'''Figura 14''': Estrutura no tempo 1x10<sup>5</sup> | |||
Arquivo:T10_3e5.png|'''Figura 15''': Estrutura no tempo 3x10<sup>5</sup> | |||
Arquivo:T10_5e5.png|'''Figura 16''': Estrutura no tempo 5x10<sup>5</sup> | |||
</gallery> | |||
<gallery widths=200px heights=200px caption="Simulação com T = 1" class="center"> | |||
Arquivo:T1_1e5.png|'''Figura 17''': Estrutura no tempo 1x10<sup>5</sup> | |||
Arquivo:T1_3e5.png|'''Figura 18''': Estrutura no tempo 3x10<sup>5</sup> | |||
Arquivo:T1_5e5.png|'''Figura 19''': Estrutura no tempo 5x10<sup>5</sup> | |||
</gallery> | |||
:: | <gallery widths=200px heights=200px caption="Simulação variando a temperatura" class="center"> | ||
Arquivo:Sweep_t10.png|'''Figura 20''': Estrutura na temperatura 10 | |||
Arquivo:Sweep_t7.png|'''Figura 21''': Estrutura na temperatura 7 | |||
Arquivo:Sweep_t4.png|'''Figura 22''': Estrutura na temperatura 4 | |||
Arquivo:Sweep_t1.png|'''Figura 23''': Estrutura na temperatura 1 | |||
</gallery> | |||
== Referências == | |||
Giordano, J., Nakanishi, H., ''Computational Physics'', 2nd ed., Pearson, 2005. | |||
Poletto, F., Material da disciplina de Química Orgânica de Biomoléculas, UFRGS, 2021. | |||
Edição atual tal como às 15h04min de 19 de maio de 2022
Carolina Lenzi
Este trabalho tem como objetivo utilizar o método de Monte Carlo para simular o enovelamento de proteínas.
Proteínas
As proteínas são moléculas com papel fundamental para os seres vivos. Elas atuam em diversos processos biológicos, como o transporte de oxigênio, a catálise de reações químicas, a defesa do organismo, a formação dos hormônios e formação de ossos e tendões. As proteínas são formadas por centenas de aminoácidos ligados em cadeia por ligações covalentes. Existem 20 aminoácidos proteinogênicos que dão origem às proteínas conhecidas e encontradas na natureza. Cada sequência de aminoácidos ligados covalentemente gera uma proteína diferente, com uma função específica no organismo. Essa sequência, bem determinada, é chamada de estrutura primária da proteína.
A proteína tende a se enovelar para minimizar a energia da sua estrutura, relativa às interações não covalentes (como ligações de hidrogênio, ponte salina, interações hidrofóbicas, interações iônicas…) entre os aminoácidos e com o meio. Isso é possível porque as ligações químicas possuem uma certa flexibilidade, que permite a rotação das moléculas. O enovelamento da estrutura primária gera regiões com padrões regulares na proteína, chamadas de estrutura secundária. Essas regiões regulares também tendem a se enovelar, dando origem a estrutura terciária da proteína. A estrutura terciária de menor energia é, geralmente, a conformação funcional da proteína, ou seja, sua configuração em estado biologicamente ativo, que é conhecida como forma nativa. Em alguns casos as estruturas terciárias podem se aglomerar e formar as estruturas quaternárias.
Como a função da proteína está diretamente relacionada com a sua forma nativa, e esta está relacionada com a sequência de aminoácidos que dá origem à proteína, é interessante conseguir prever a estrutura terciária a partir da estrutura primária, com a finalidade de desenvolver proteínas com características específicas. Esse é um dos grandes problemas da bioinformática atualmente. Além da complexidade de compreender a termodinâmica e o mecanismo do enovelamento, a proteína encontra a estrutura ótima em fração de segundo, mas o tempo que seria necessário para testar aleatoriamente as estruturas possíveis para encontrar a de menor energia é maior que a idade do universo, como apontado no paradoxo de Levinthal.
Simulação de Monte Carlo
A simulação do enovelamento foi feita com base no livro do Giordano e envolve um modelo muito simplificado do que acontece na realidade.
Consideramos uma cadeia de N aminoácidos, sorteados dentre os 20 possíveis, para montar a estrutura primária da proteína, representada por um vetor de tamanho N. Aminoácidos em posições adjacentes do vetor são considerados ligados covalentemente. A cadeia é colocada em uma rede quadrada de tamanho NxN, para permitir que a proteína esteja completamente desenovelada (esticada).
Em cada posição da rede, um aminoácido tem no máximo 4 aminoácidos vizinhos mais próximos com os quais pode interagir ou estar ligado (figura 4) e no máximo 8 posições vizinhas para as quais ele pode se mover (figura 5).
Para as interações de não covalentes entre os aminoácidos, consideramos as seguintes forças atuantes:
- Forças de van der Waals: força atrativa para aminoácidos próximos, que perde o efeito com o aumento da distancia entre os aminoacidos;
- Ligações de hidrogênio: ligações entre aminoácidos próximos na rede;
- Interação com a água (hidrofilicidade e hidrofobia): aminoácidos hidrofílicos são atraídos pela água presente no meio e, por isso, tendem a manter a cadeia não enovelada. Já os hidrofóbicos repelem a água do meio e preferem uma estrutura enovelada.
Todas essas forças estão competindo no processo de enovelamento da proteína. Para o modelo, agrupamos essas interações em uma energia Jij, associada a um par de aminoácidos vizinhos na rede, A(m) e A(n) nas posições i e j, e não ligados covalentemente, ou seja, não adjacentes na cadeia. A energia da estrutura é dada pela soma sobre todos os pares de aminoácidos da proteína:
onde se os aminoácidos m e n são vizinhos na rede e não estão ligados covalentemente, e zero caso contrário.
A energia J pode ser pensada como uma matriz 20x20 contendo as interações relativas a todos os pares de aminoácidos, porém a matriz é simétrica, portanto, podemos guardar apenas 210 valores correspondentes aos pares distintos de aminoácidos.
Com essas definições, podemos partir para a simulação de Monte Carlo, esquematizada a seguir. O código foi implementado em C, e se encontra no Github
- Inicializar a cadeia e posicionar na rede
- Sortear um aminoácido da cadeia e encontrar sua posição na rede
- Calcular a energia inicial (Ei) da estrutura
- Sortear um dos 8 vizinhos da posição do aminoácido
- Verificar se é possível mover o aminoácido para a posição vizinha sorteada
- Se possível, mover o aminoácido e calcular a energia da nova estrutura (Ef)
- Se Ef < Ei, aceitar o movimento
- Se Ef >= Ei, aceitar o movimento com probabilidade do fator de Boltzmann
- Desfazer o movimento se ele não for aceito
- Contar um tempo de Monte Carlo a cada sorteio de vizinho
- Repetir a partir do passo 2.
A simulação consiste em repetir esses passos (a partir do 2) por longos tempos de Monte Carlo.
Resultados
Em todas as simulações, foi utilizada a mesma cadeia de 15 aminoácidos e os mesmos valores de energia Jij, que foram sorteados dentro do intervalo [-4, -2]. As energias foram medidas em unidades de kB por simplicidade. Incicialmente, a cadeia foi colocada esticada no meio da rede, como mostra a figura 6. Os gráficos foram gerados no gnuplot e as figuras da rede e das estruturas foram feitas no GIMP.
OBS: não foram utilizadas condições de contorno periódicas.
Nas figuras a seguir, temos a energia e o tamanho da cadeia (calculado como a distância ponta a ponta da cadeia) em função do tempo de simulação. Essa simulação foi feita com temperatura T = 10 e um total de 5x105 tempo de Monte Carlo. A temperatura alta permite que a proteína explore várias configurações e teste estruturas de diferentes energias, por isso, o gráfico tem tanta flutuação. Como várias estruturas diferentes são testadas, algumas são mais abertas e outras mais compactas, então o tamanho da cadeia também flutua bastante.
A simulação também foi feita para a temperatura T = 1, com o mesmo tempo de 5x105 tempo de Monte Carlo, e o resultado está nas figuras abaixo. As flutuações são menores e a proteína passa mais tempo em estruturas com energias mais baixas, porque a baixa temperatura não permite tanta movimentação. O tamanho também varia menos, e a proteína fica em estruturas mais compactas.
Outra simulação foi realizada partindo de uma temperatura alta e reduzindo-a gradativamente, para permitir que a proteína explore várias configurações nas temperaturas mais altas e consiga escolher uma de energia mais baixa. Em cada temperatura, a proteína passou 20x105 tempo de Monte Carlo. Os resultados, apresentados a seguir, são da média da energia e do tamanho em cada temperatura, e também a variância da energia em função da temperatura.
Percebemos, pelas figuras 11 e 12, que a energia da estrutura da proteína diminui com a temperatura, até T = 2, aproximadamente, onde não há mais uma mudança perceptível na energia. Isso indica que a proteína encontrou uma estrutura estável com energia baixa. A figura 13 também mostra estabilidade para temperaturas abaixo de 2, indicando que o estado enovelado da proteína não sofre alteração. Nesse caso, a estrutura encontrada pela proteína não é a mais compacta, mas é a de menor energia, dentre as testadas. OBS: O resultado para o tamanho em função da temperatura não era o esperado, a curva deveria seguir a mesma tendência do gráfico da energia. Falta analisar o porquê disso.
A seguir, algumas estruturas testadas pela proteína durante as simulações.
- Simulação com T = 10
- Simulação com T = 1
- Simulação variando a temperatura
Referências
Giordano, J., Nakanishi, H., Computational Physics, 2nd ed., Pearson, 2005.
Poletto, F., Material da disciplina de Química Orgânica de Biomoléculas, UFRGS, 2021.