Shooting method e Método de Crank-Nicolson aplicados à Equação de Schrödinger

O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson.

Equação de Schrödinger

A equação de Schrödinger unidimensional pode ser escrita da seguinte maneira:

$i\hbar {\frac {\partial \Psi }{\partial t}}=-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}+V\Psi .$

Para resolvê-la é necessário efetuar uma separação de variáveis:

$\Psi (x,t)=\psi (x)\varphi (t).$

Aplicando na primeira equação e separando os termos espaciais dos termos temporais, chega-se a uma equação com o seguinte formato:

$i\hbar {\frac {1}{\varphi }}{\frac {d\varphi }{dt}}=-{\frac {\hbar ^{2}}{2m}}{\frac {1}{\psi }}{\frac {d^{2}\psi }{dx^{2}}}+V.$

Pelo fato da parte da esquerda ser dependente de t e a parte da direita ser dependente de x e de ambas estarem relacionadas por uma igualdade, é necessário que ambos os lados sejam constantes: em outras palavras, não é possível modificar um lado sem necessariamente alterar o outro. Através de um raciocínio perspicaz, a constante em questão será denominada E.

Parte temporal

A parte que diz respeito à evolução temporal:

${\frac {d\varphi }{dt}}=-{\frac {iE}{\hbar }}\varphi .$

A solução geral possui o seguinte formato

$\varphi (t)=Ce^{-{\frac {-iEt}{\hbar }}},$

cuja constante C pode, neste caso, ser absorvida, de modo que

$\varphi (t)=e^{-{\frac {-iEt}{\hbar }}}.$

Parte espacial

Quanto à parte espacial, utilizando o mesmo raciocínio empregado anteriormente, a equação pode ser escrita como

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V\psi =E\psi$

Para este caso, no entanto, não há uma única solução, pois esta depende do potencial V escolhido. Para o presente trabalho optou-se por trabalhar com o caso do poço infinito de potencial pelo fato das soluções analíticas já serem conhecidas, de modo a tornar possível avaliar os resultados numéricos obtidos à luz da solução analítica.

Poço de potencial infinito

Esquematicamente, tem-se:

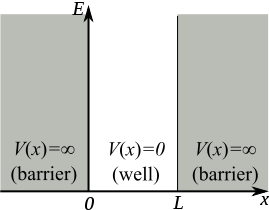
Poço de potencial infinito

O potencial pode ser descrito como:

$V(x)={\begin{cases}0,&{\mbox{se }}0\leq x\leq L,\\\infty ,&{\mbox{de outra forma.}}\end{cases}}$

Dentro do poço, onde $V=0$, o problema pode ser modelado da seguinte maneira

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi ,$

ou

${\frac {d^{2}\psi }{dx^{2}}}=-k^{2}\psi ,$

onde

$k\equiv {\frac {\sqrt {2mE}}{\hbar }}.$

A solução é dada por

$\psi (x)=Asen(kx)+Bcos(kx).$

Aplicando as condições de contorno $\psi (0)=\psi (L)=0$ e efetuando a normalização da função de onda, obtém-se a solução geral

$\psi _{n}(x)={\sqrt {\frac {2}{L}}}sen\left({\frac {n\pi }{L}}x\right),$

cujas energias discretizadas são

$E_{n}={\frac {\hbar ^{2}k_{n}^{2}}{2m}}={\frac {n^{2}\pi ^{2}\hbar ^{2}}{2mL^{2}}}.$

Utilizando a equação acima, pode-se calcular os valores da energia de cada estado estacionário. Para o caso de um elétron, as energias referentes aos três estados estacionários são $E_{1}=0,376$ eV, $E_{2}=1,504$ eV e $E_{3}=3,384$ eV.

Na próxima seção será feita uma estimativa dos valores acima expostos através do "Shooting method".

Shooting Method

Muitos métodos numéricos (e.g. Runge-Kutta, Forward Euler) requerem os valores da função e de sua derivada no ponto inicial. Acontece que podem haver problemas em que estes valores não estarão disponíveis, principalmente o valor da derivada em questão. Uma alternativa seria conjecturar o valor da condição inicial e integrar, através de um método apropriado, em direção à outra condição de contorno: um "chute" apropriado faria com que a integração evoluísse e retornasse um valor muito próximo, a depender da acurácia necessária, ao da condição de contorno. A ideia seria executar os seguintes passos:

1. Supor um valor para a condição de contorno desconhecida (e.g. $y(0)$ ou $y'(0)$);
2. Integrar o problema através de um método conhecido até a próxima condição de contorno (e.g., $y(L)$);
3. Se o chute inicial não fez com que o sistema evoluísse até $y(L)$, então deve-se supor outro valor para a condição inicial e repetir o procedimento.

O método descrito acima de forma simplificada recebe o nome, em inglês, de Shooting method, o que em português seria algo como "Método do tiro" ou "Método do chute". Na próxima seção esse método será aplicado para o caso do poço infinito de potencial.

Poço de potencial infinito

Seja a equação ${\frac {d^{2}\psi }{dx^{2}}}=-k\psi E$, onde $k={\frac {2m}{\hbar ^{2}}}$.

Escrevendo com outra notação: ${\ddot {\psi }}=-k\psi E$.

Dividindo o problema em $\Delta x$'s pequenos, pode-se reescrever a equação acima da seguinte forma:

${\ddot {\psi }}={\frac {\Delta {\dot {\psi }}}{\Delta x}}={\frac {{\dot {\psi _{2}}}-{\dot {\psi _{1}}}}{\Delta x}}\implies {\dot {\psi _{2}}}={\ddot {\psi }}\Delta x+{\dot {\psi _{1}}}$

.

Também:

${\dot {\psi }}={\frac {\Delta \psi }{\Delta x}}={\frac {\psi _{2}-\psi _{1}}{\Delta x}}\implies \psi _{2}={\dot {\psi }}\Delta x+\psi _{1}$

.

Além disso:

$\Delta x=x_{2}-x_{1}\implies x_{2}=x_{1}+\Delta {x}$

.

A integração, então, é realizada utilizando as relações 8, 9, 10 e 11, até que se atinja a borda do poço, isto é, $x=L$.

Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que $\psi (0)=0$, de modo que $\psi _{1}=0$. No entanto, o valor da derivada ${\dot {\psi _{1}}}$ não é conhecido, de modo que supõe-se que seja uma constante, a saber, ${\dot {\psi _{1}}}=1$. Chutando que $E=0$, utilizando a massa do elétron e $L=1$, obtém-se a primeira solução estacionária:

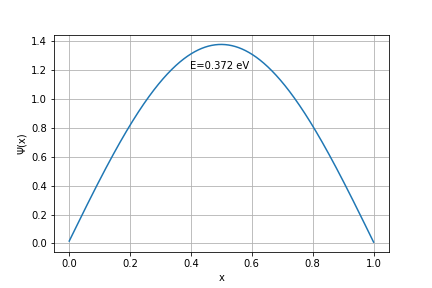
Solução estacionária (n=1)

Pode-se observar que o valor de energia obtido numericamente é cerca de 4% menor do que aquele obtido analiticamente.

Para o caso n=2:

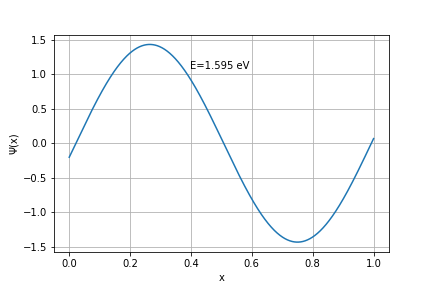
Solução estacionária (n=2)

Aqui, o valor obtido numericamente é aproximadamente 5% maior do que o valor obtido analiticamente.

Para o caso n=3:

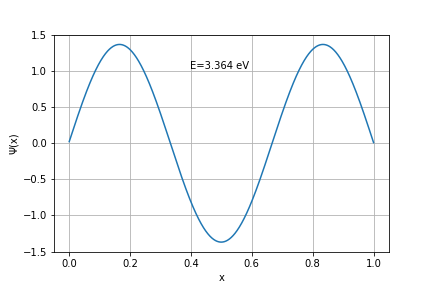
Solução estacionária (n=3)

Para este caso, o valor numérico é cerca de 1% menor do que o valor analítico.

Método de Crank-Nicolson

Seja a equação diferencial

${\frac {\partial f}{\partial t}}=L_{1}{\textbf {r}}f({\textbf {r}},t)$

,

onde $L_{\textbf {r}}$ é um operador diferencial linear em r.

Em forma discretizada no tempo, pode-se escrever

$f^{n+1}({\textbf {r}})-f^{n}({\textbf {r}})=L_{\textbf {r}}f^{n}({\textbf {r}})dt$

.

Por simetria, pode-se escrever a equação acima utilizando um f à direita:

$f^{n+1}({\textbf {r}})-f^{n}({\textbf {r}})=L_{\textbf {r}}f^{n+1}({\textbf {r}})dt.$

A equação acima é dita "explícita" pois, para o cálculo de $f^{n+1}$, só é utilizado o valor já explicitamente calculado $f^{n}$. Já a equação anterior é chamada implícita pois $f^{n+1}$ está presente explicitamente. Em termos numéricos, um método peca pelo excesso enquanto o outro o faz pela falta, de modo que um resultado mais satisfatório pode ser obtido ao tomar-se a média dos dois:

$f^{n+1}({\textbf {r}})-f^{n}({\textbf {r}})={\frac {dt}{2}}(L_{\textbf {r}}f^{n+1}({\textbf {r}})+L_{\textbf {r}}f^{n}({\textbf {r}})).$

Após alguma álgebra:

$f^{n+1}({\textbf {r}})=\left(1-{\frac {dt}{2}}L_{\textbf {r}}\right)^{-1}\left(1+{\frac {dt}{2}}L_{\textbf {r}}\right)f^{n}({\textbf {r}})$

.

Chamando $M=I+{\frac {dt}{2}}L_{\textbf {r}}$ e $E=I-{\frac {dt}{2}}L_{\textbf {r}}$, onde I indica a matriz identidade, pode-se reescrever a equação acima na seguinte maneira:

$f^{n+1}=E^{-1}Mf^{n}$

.

Trata-se do método de Crank-Nicolson, mais estável e preciso do que os métodos implícito e explícito. Caso o problema apresentar condições de contorno, estas serão devidamente implementadas nos elementos das matrizes M e E.

Equação de Schrödinger

Seja a equação de Schrödinger unidimensional

$i\hbar {\frac {\partial \Psi }{\partial t}}=-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}+V\Psi$

.

Efetuando a discretização das variáveis através do Método de Crank-Nicolson, obtém-se:

${\frac {\partial \Psi }{\partial t}}={\frac {\Psi _{j}^{n+1}-\Psi _{j}^{n}}{\Delta t}};$ ${\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}={\frac {\hbar ^{2}}{2m}}\left[{\frac {(\Psi _{j+1}^{n+1}-2\Psi _{j}^{n+1}+\Psi _{j-1}^{n+1})+(\Psi _{j+1}^{n}-2\Psi _{j}^{n}+\Psi _{j-1}^{n})}{2\Delta x^{2}}}\right];$ $V\Psi ={\frac {1}{2}}[V_{j}^{n+1}\Psi _{j}^{n+1}+V_{j}^{n}\Psi _{j}^{n}].$

Substituindo as discretizações na eq. de Schrödinger:

$i\left({\frac {\Psi _{j}^{n+1}-\Psi _{j}^{n}}{\Delta t}}\right)=-{\frac {\hbar ^{2}}{4m(\Delta x)^{2}}}\left[(\Psi _{j+1}^{n+1}-2\Psi _{j}^{n+1}+\Psi _{j-1}^{n+1})+(\Psi _{j+1}^{n}-2\Psi _{j}^{n}+\Psi _{j-1}^{n})\right]+{\frac {1}{2}}[V_{j}^{n+1}\Psi _{j}^{n+1}+V_{j}^{n}\Psi _{j}^{n}].$

Supondo $\hbar =m=1$ e separando as partes explícita e implícita, obtém-se, após alguma álgebra:

$\Psi _{j}^{n+1}\left[1+{\frac {i\Delta t}{2}}\left({\frac {1}{\Delta x^{2}}}+V_{j}^{n+1}\right)\right]+\Psi _{j-1}^{n+1}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]+\Psi _{j+1}^{n+1}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]=\Psi _{j}^{n}\left[1-{\frac {i\Delta t}{2}}\left({\frac {1}{\Delta x^{2}}}+V_{j}^{n}\right)\right]+\Psi _{j-1}^{n}\left[-{\frac {i\Delta t}{4\Delta x^{2}}}\right]+\Psi _{j+1}^{n}\left[{\frac {i\Delta t}{4\Delta x^{2}}}\right].$

Definindo

$a\equiv {\frac {-i\Delta t}{4(\Delta x)^{2}}}$

e

$b_{j}\equiv \left(1+{\frac {i\Delta t}{2}}\right)\left({\frac {1}{\Delta x^{2}}}+V_{j}\right),$

obtém-se:

$\Psi _{j}^{n+1}b_{j}+\Psi _{j-1}^{n+1}a+\Psi _{j+1}^{n+1}a=\Psi _{j}^{n}b_{j}^{*}+\Psi _{j-1}^{n}a^{*}+\Psi _{j+1}^{n}a^{*}.$

A equação acima pode ser escrita em forma matricial, de modo que:

${\hat {C}}\Psi ^{n+1}={\hat {D}}\Psi ^{n},$

onde

${\hat {C}}={\begin{bmatrix}b_{0}&a&0&&...&0\\a&b_{1}&a&0&...&0\\0&a&b_{2}&a&0&0\\0&0&\ddots &\ddots &\ddots \\...&...&...&a&b_{j-1}&a\\0&0&...&0&a&b_{j}\\\end{bmatrix}}$

e

${\hat {D}}={\begin{bmatrix}b_{0}^{*}&a&0&&...&0\\a^{*}&b_{1}^{*}&a^{*}&0&...&0\\0&a^{*}&b_{2}^{*}&a^{*}&0&0\\0&0&\ddots &\ddots &\ddots \\...&...&...&a^{*}&b_{j-1}^{*}&a^{*}\\0&0&...&0&a^{*}&b_{j}^{*}\\\end{bmatrix}}$

Para avaliar a evolução temporal do sistema, é necessário encontrar $\Psi ^{n+1}$. Utilizando resultados anteriores, pode-se obter $\Psi ^{n+1}$ através da seguinte relação:

$\Psi ^{n+1}={\hat {C}}^{-1}{\hat {C^{*}}}\Psi ^{n}$

Poço de potencial infinito

Para o presente caso a ideia é obter a evolução temporal do sistema, impondo condições de contorno iguais a zero, de modo que os operadores ${\hat {C}}$ e ${\hat {D}}$ ficam:

${\hat {C}}={\begin{bmatrix}1&0&0&&...&0\\a&b&a&0&...&0\\0&a&b&a&0&0\\0&0&\ddots &\ddots &\ddots \\...&...&...&a&b&a\\0&0&...&0&0&1\\\end{bmatrix}}$

e

${\hat {D}}={\begin{bmatrix}1&0&0&&...&0\\a^{*}&b^{*}&a^{*}&0&0...&0\\0&a^{*}&b^{*}&a^{*}&0&0\\0&0&\ddots &\ddots &\ddots \\...&...&...&a^{*}&b^{*}&a^{*}\\0&0&...&0&0&1\\\end{bmatrix}}$

A ideia é que o primeiro e o último termo do tanto do vetor $\Psi ^{n}$ quanto do vetor $\Psi ^{n+1}$ seja constante, o que satisfaz as condições de contorno do presente caso. Também é interessante notar que os índices $b$ são todos constantes, visto que no presente caso o potencial dentro do poço é nulo.

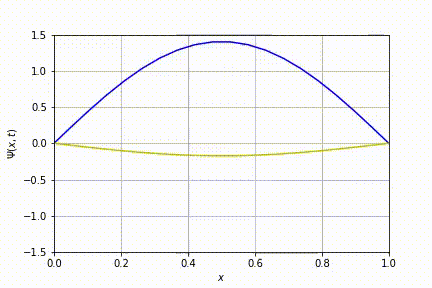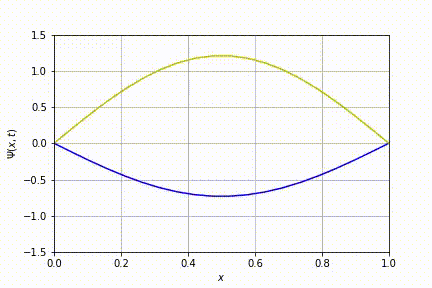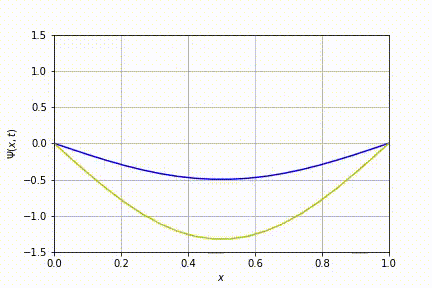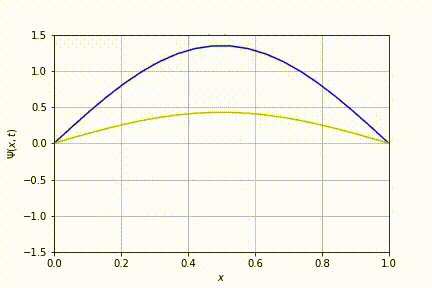
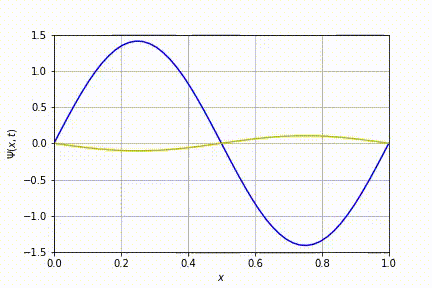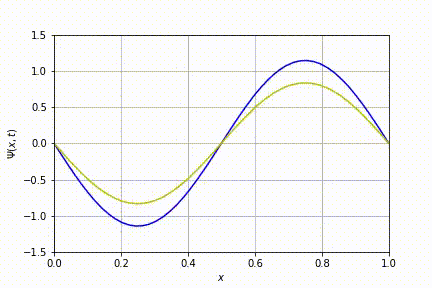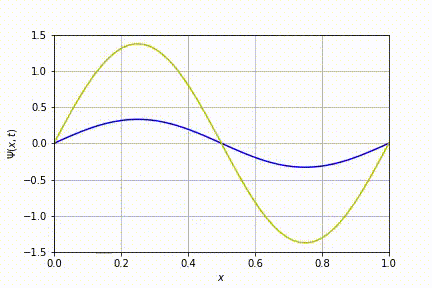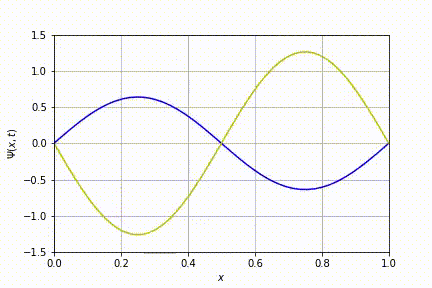
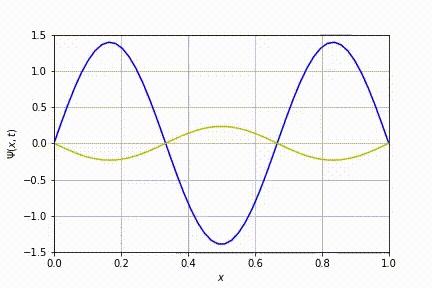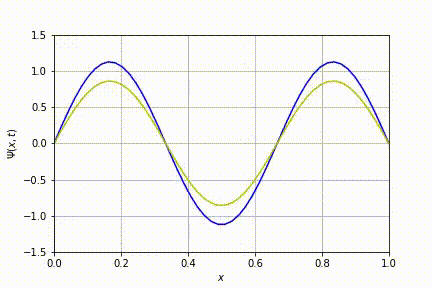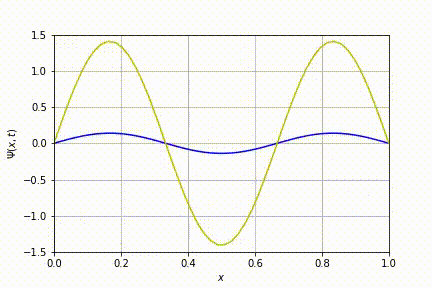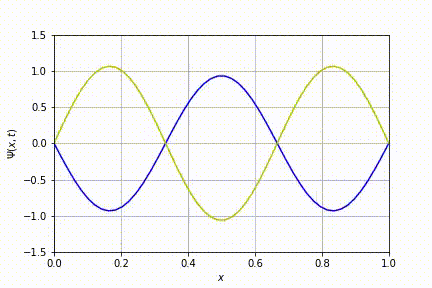
Implementando o algoritmo descrito acima, obteve-se:

Evolução temporal (n=1)

Evolução temporal para o caso n=1. Nesta animação e nas subsequentes, foram sobrepostas as partes real e imaginária da equação de Schrödinger: a linha azul diz respeito à parte real enquanto a amarela, à imaginária.

Evolução temporal (n=2)

Na figura acima, tem-se a evolução do caso n=2.

Evolução temporal (n=3)

Por último, o caso n=3.