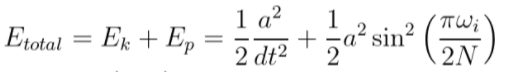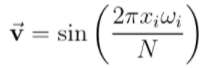Problema de Fermi-Pasta-Ulam: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (27 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 8: | Linha 8: | ||
<center><div><ul> | <center><div><ul> | ||
<li style="display: inline-block;"> [[Arquivo:Springs.png|thumb|437px|Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas.]] </li> | <li style="display: inline-block;"> [[Arquivo:Springs.png|thumb|437px|Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas<ref name= FPU>https://www.respondeai.com.br/conteudo/fisica/mhs-e-mha/oscilacoes-acopladas/951</ref>.]] </li> | ||
</li> | </li> | ||
</ul></div></center> | </ul></div></center> | ||
| Linha 14: | Linha 14: | ||
A lei de forças que rege o comportamento deste sistema é: | A lei de forças que rege o comportamento deste sistema é: | ||
<math> | <math> F_{i} = -k \Delta x - \alpha k \Delta x^2 - \beta k \Delta x^3 </math>. | ||
Onde <math> \Delta x </math> e a deformação a cada 2 massas acopladas (<math> x_{i+1} - x_i </math>), <math> k </math> é a constante elástica da mola, <math> \alpha </math> é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e <math> \beta </math> é o parâmetro que controla a correção cúbica. Importante ressaltar que se <math> \alpha </math> | Onde <math> \Delta x </math> e a deformação a cada 2 massas acopladas (<math> x_{i+1} - x_i </math>), <math> k </math> é a constante elástica da mola (aqui considerado, <math> \alpha </math> é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e <math> \beta </math> é o parâmetro que controla a correção cúbica. Importante ressaltar que se <math> \alpha </math> assumir um valor não nulo, real, <math> \beta </math> é igual a zero no nosso sistema, ou vice-versa. Não estamos analisando correções quadráticas somadas com correções cúbicas neste trabalho. | ||
=== Motivação | === Motivação === | ||
''' | '''O paradoxo Enrico Fermi, John R. Pasta, Stanislaw M. Ulam e Mary Tsingou'''<ref name= FPUT1> https://www.scielo.br/j/rbef/a/SkRCy5fdnGbhfxNjpx5BkRD/?format=pdf&lang=pt - O problema Fermi-Pasta-Ulam-Tsingou: Equiparticão de | ||
energia vista através de simulações computacionais </ref> | |||
A premissa inicial do paradoxo de FPUT consiste no Teorema da Equipartição de Energia. O sistema consistia em uma corrente de partículas, com as extremidades fixas, que interagiam entre seus vizinhos somente com forças elásticas (as forças teriam um termo linear como a Força de Hooke e mais um termo não-linear, podendo ser quadrático ou cúbico). Era esperado que a energia total fosse distribuída igualmente entre as partículas. No caso em questão, a distribuição de energia entre as partículas pode ser descrita através dos seus modos normais de vibração. | |||
A análise do problema gerou um paradoxo que começaria a ser respondido somente 10 anos depois, o que ajudou no desenvolvimento das teorias de sólitons e do caos. Pretendia-se observar a distribuição uniforme de energia entre os diversos modos normais de vibração com o passar do tempo (ao longo das iterações da simulação computacional). Isso significaria que o sistema alcançou um equilíbrio térmico e seria uma exemplificação computacional do Teorema de Equipartição de Energia. Caso as forças entre as partículas fossem estritamente lineares, isso não ocorreria, pois a energia alocada em cada modo não conseguiria acessar outros modos. Imaginava-se que uma componente não-linear na força tornaria acessível qualquer modo de vibração, porém não foi o observado. | |||
A princípio, foi observada a tendência do sistema de distribuir a energia. O primeiro modo de vibração antes estimulado, perdeu energia ao longo do tempo, a qual começou a se alocar nos modos de energia mais baixos. Entretanto, por um descuido, deixaram a simulação decorrer por um tempo maior do que era planejado. Ao retornar ao laboratório para corrigir tal erro, se depararam com um resultado inesperado. A energia, que supostamente deveria estar igualmente partilhada entre os modos de vibração, estava quase completamente alocada no primeiro modo de vibração. De fato, somente 3% da energia não estava presente no primeiro modo. Devido a esta observação, deixaram a simulação correr por ainda mais tempo. Notaram, então, que existia | |||
um ciclo, no qual a energia saía do primeiro modo de vibração, começava a se distribuir nos modos mais baixos, para, por fim, voltar quase que inteiramente para o primeiro modo de vibração. Contudo, em 2015, relatou-se que o sistema FPUT poderia atingir equipartição de energia pelo menos entre modos normais livres (interação entre três fônons). | |||
== Discretização == | == Discretização == | ||
| Linha 29: | Linha 34: | ||
A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso <ref name=wiki>https://en.wikipedia.org/wiki/Fermi%E2%80%93Pasta%E2%80%93Ulam%E2%80%93Tsingou_problem</ref>. Partimos do problema com correção quadrática, ou seja, <math> \beta = 0 </math>. Partindo de: | A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso <ref name=wiki>https://en.wikipedia.org/wiki/Fermi%E2%80%93Pasta%E2%80%93Ulam%E2%80%93Tsingou_problem</ref>. Partimos do problema com correção quadrática, ou seja, <math> \beta = 0 </math>. Partindo de: | ||
<math> | <math> F_{i} = -k \Delta x - \alpha k \Delta x^2 </math>, | ||
substituímos pelas variáveis discretas: | |||
<math> m \ddot{x_j} = -k \left( (x_{j+1} - x_j) - (x_j - x_{j-1}) \right) - \alpha k \left( (x_{j+1} - x_j) - (x_j - x_{j-1}) \right) </math>, | <math> m \ddot{x_j} = -k \left( (x_{j+1} - x_j) - (x_j - x_{j-1}) \right) - \alpha k \left( (x_{j+1} - x_j)^2 - (x_j - x_{j-1})^2 \right) </math>, | ||
Chegamos em: | Sendo que as partículas de índice zero e N estão fixas, Chegamos em: | ||
<math> m \ddot{x_j} = k \left( x_{j+1} - 2x_{j} + x_{j-1} \right) \left[ 1 + \alpha \left( x_{j+1} - x_{j-1} \right) \right] </math> | <math> m \ddot{x_j} = k \left( x_{j+1} - 2x_{j} + x_{j-1} \right) \left[ 1 + \alpha \left( x_{j+1} - x_{j-1} \right) \right] </math>, | ||
Em que <math> \ddot{x_j} </math> é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas. | Em que <math> \ddot{x_j} </math> é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas. | ||
A Energia do sistema é calculada para cada ciclo de oscilação, porém para obtermos os resultados dos modos de oscilação e compararmos com os estudos atuais e o original de de FPUT, calculamos a energia dos primeiros modos de vibração da corda para demonstrar o comportamento visivelmente periódico destas energias. É possível calcular a energia dos modos de vibração através da equação: | |||
[[Arquivo:Eq1.PNG|350px]] | |||
em que <math> a</math> é o vetor das posições projetado num vetor de um seno com a frequência do modo que queremos plotar: | |||
[[Arquivo:Eq2.PNG|120px]] | |||
< | e: | ||
</ | |||
[[Arquivo:Eq3.PNG|150px]] | |||
<math>N</math> é o número de partículas e <math>\omega_i = \sqrt{\frac{k}{m}} </math> | |||
== Resultados == | == Resultados == | ||
O sistema foi iniciado com o modo normal de oscilação 1 (seno com frequência <math>\omega = \sqrt{\frac{k}{m}}</math>), com velocidades iniciais igual a zero de cada partícula. O movimento começa apenas pelas forças já presentes entre cada partículas, pelas equações apresentadas acima. | |||
[[Arquivo:Estado inicial das particulas.png|center|thumb|500px|legenda.]] | [[Arquivo:Estado inicial das particulas.png|center|thumb|500px|legenda.]] | ||
Segue abaixo a evolução do sistema ao longo do tempo, apenas para gerar o .gif considerando: | |||
<math> | <math> | ||
\begin{cases} | \begin{cases} | ||
\alpha = 1,2 \\ | |||
k = 0,95 \\ | |||
m = 1,05 \\ | |||
N = 30 \\ | |||
t_{max} = 4000 \\ | |||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
[[Arquivo:Corda final.gif|center|thumb|500px|Simulação FPU para o problema proposto.]] | |||
Já os resultados das energias, consideramos todas constantes iguais à 1, mais de 100 partículas e o número de iterações está em cada imagem. Procedemos de duas formas: calculamos a porcentagem de cada modo normal de oscilação pela Transformada de Fourier (para selecionar as frequências que estavam presentes na oscilação, sem calcular as energias), o que apresentou um comportamento muito similar às energias calculadas pela soma de energias cinética e potencial: | |||
[[Arquivo:Energias fft.jpeg|thumb|700px|center|Porcentagem de cada modo vibracional ao longo do tempo. A escala do tempo foi reduzida em 20 vezes para melhor apresentação do gráfico.]] | |||
E também calculamos pela equação de energia citada acima, obtivemos os seguintes comportamentos: | |||
<center><div><ul> | |||
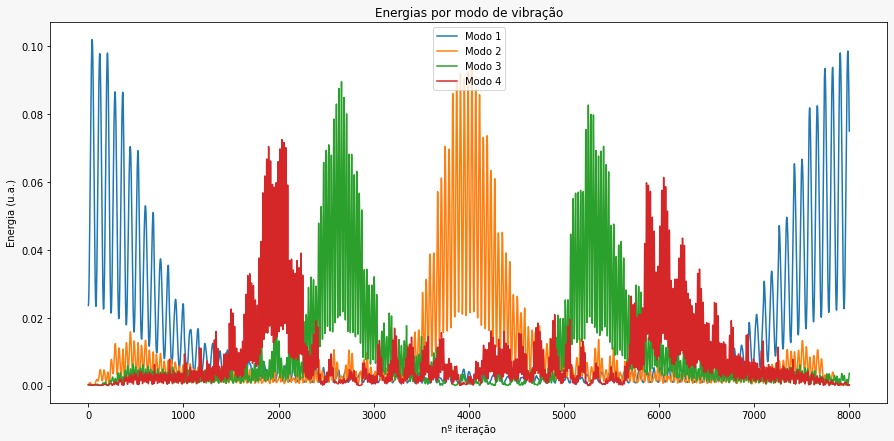
<li style="display: inline-block;"> [[Arquivo:Energias certo1.jpeg|500px|thumb|Energias por modo de oscilação. A escala do tempo está aumentada em 2 vezes.]]</li> | |||
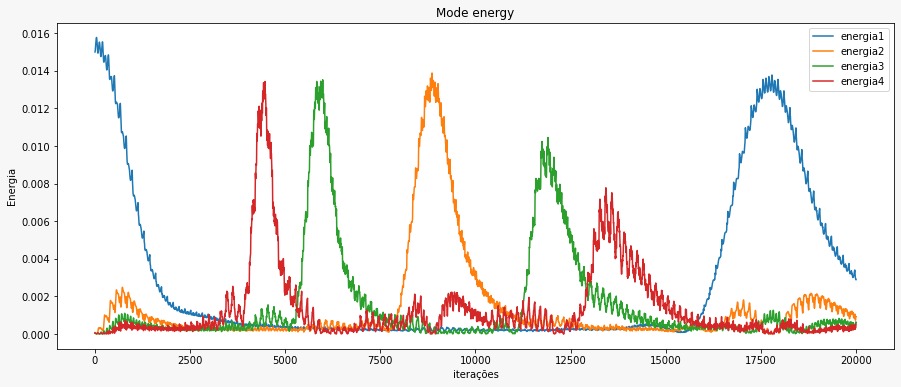
<li style="display: inline-block;"> [[Arquivo:Energias certo2.jpg|520px|thumb|Energias por modo de oscilação com fft. A escala do tempo está aumentada em 5 vezes.]]</li> | |||
</ul></div></center> | |||
A expressão utilizada para calcular estas energias foi a memsa citada anteriormente: | |||
[[Arquivo:Eq1.PNG|center|350px]] | |||
== Discussões == | == Discussões == | ||
Como o intuito era replicar os resultados através da simulação com dinâmica molecular obtivemos resultados muito parecidos comparando estudos já realizados sobre este problema | Como o intuito era replicar os resultados e o comportamento das energias através da simulação com dinâmica molecular, obtivemos resultados muito parecidos comparando estudos já realizados sobre este problema <ref name=FPUT1></ref>. | ||
A questão de simular a energia usando a porcentagens dos senos também faz sentido pensando ''quanta contribuição'' o modo normal de oscilação tem no movimento atual, como pudemos ver que o comportamento foi bem similar ao das energias calculadas. | |||
== Implementação == | == Implementação == | ||
Implementamos a iteração do movimento das partículas por Velocity-Verlet. | |||
A questão de variar os parâmetros do problema, como já mencionado previamente nesta wiki, e também apresentado nos gráficos e no gif, vimos que não interferia muito no caráter dos resultados (e o quanto isso poderia influenciar no paradoxo de equipartição de energia), porém o fizemos para gerar imagens melhores e o gif com menos de 2 MB. | |||
<source lang="haskell" line='line'> | <source lang="haskell" line='line'> | ||
| Linha 98: | Linha 128: | ||
def posicao(pos, velo, dt): | def posicao(pos, velo, dt): | ||
size = len( | size = len(pos) | ||
new_posY = [0.0 for i in range(size)] | new_posY = [0.0 for i in range(size)] | ||
for i in range(size): | for i in range(size): | ||
new_pos[i] = pos[i] + new_velo[i]*dt | |||
return | return new_pos | ||
N = número de partículas | N = número de partículas | ||
| Linha 115: | Linha 145: | ||
velo = velocidade(veloY, new_aceY,dt) | velo = velocidade(veloY, new_aceY,dt) | ||
pos = posicao(posY_old, veloY, dt) | pos = posicao(posY_old, veloY, dt) | ||
calcula_energias(pos) | |||
pos_old = pos.copy() #sem ".copy()" o python usa o mesmo endereço de memória para 2 variáveis | pos_old = pos.copy() #sem ".copy()" o python usa o mesmo endereço de memória para 2 variáveis | ||
| Linha 121: | Linha 152: | ||
gera_gif() | gera_gif() | ||
</source> | </source> | ||
== Link para Códigos == | == Link para Códigos == | ||
Fizemos no ambiente Colab em ''.ipynb'', segue link do github:[https://github.com/padovanih/ | Fizemos no ambiente Colab em ''.ipynb'', segue link do github:[https://github.com/padovanih/Fermi-Pasta-Ulam] | ||
== Referências == | == Referências == | ||
<references/> | <references/> | ||
Edição atual tal como às 23h27min de 28 de maio de 2021
Grupo: Augusto M Giani e Henrique Padovani
O objetivo deste trabalho é replicar os resultados do problema proposto por Fermi-Pasta-Ulam em 1953 [1] sobre sistemas dinâmicos não lineares. As análises serão sobre a solução dos modos de vibração comparados à solução analítica para poucas massas e também sobre a energia do sistema para os modos de oscilação, enquanto o sistema evolui no tempo.
O Problema
O Problema proposto constitui-se de simulações em uma rede de partículas ligadas entre si através de molas que obedecem a Lei de Hooke com uma correção não-linear quadrática ou cúbica [2]
-
 Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas[2].
Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas[2].
A lei de forças que rege o comportamento deste sistema é:
.
Onde e a deformação a cada 2 massas acopladas (), é a constante elástica da mola (aqui considerado, é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e é o parâmetro que controla a correção cúbica. Importante ressaltar que se assumir um valor não nulo, real, é igual a zero no nosso sistema, ou vice-versa. Não estamos analisando correções quadráticas somadas com correções cúbicas neste trabalho.
Motivação
O paradoxo Enrico Fermi, John R. Pasta, Stanislaw M. Ulam e Mary Tsingou[3]
A premissa inicial do paradoxo de FPUT consiste no Teorema da Equipartição de Energia. O sistema consistia em uma corrente de partículas, com as extremidades fixas, que interagiam entre seus vizinhos somente com forças elásticas (as forças teriam um termo linear como a Força de Hooke e mais um termo não-linear, podendo ser quadrático ou cúbico). Era esperado que a energia total fosse distribuída igualmente entre as partículas. No caso em questão, a distribuição de energia entre as partículas pode ser descrita através dos seus modos normais de vibração.
A análise do problema gerou um paradoxo que começaria a ser respondido somente 10 anos depois, o que ajudou no desenvolvimento das teorias de sólitons e do caos. Pretendia-se observar a distribuição uniforme de energia entre os diversos modos normais de vibração com o passar do tempo (ao longo das iterações da simulação computacional). Isso significaria que o sistema alcançou um equilíbrio térmico e seria uma exemplificação computacional do Teorema de Equipartição de Energia. Caso as forças entre as partículas fossem estritamente lineares, isso não ocorreria, pois a energia alocada em cada modo não conseguiria acessar outros modos. Imaginava-se que uma componente não-linear na força tornaria acessível qualquer modo de vibração, porém não foi o observado.
A princípio, foi observada a tendência do sistema de distribuir a energia. O primeiro modo de vibração antes estimulado, perdeu energia ao longo do tempo, a qual começou a se alocar nos modos de energia mais baixos. Entretanto, por um descuido, deixaram a simulação decorrer por um tempo maior do que era planejado. Ao retornar ao laboratório para corrigir tal erro, se depararam com um resultado inesperado. A energia, que supostamente deveria estar igualmente partilhada entre os modos de vibração, estava quase completamente alocada no primeiro modo de vibração. De fato, somente 3% da energia não estava presente no primeiro modo. Devido a esta observação, deixaram a simulação correr por ainda mais tempo. Notaram, então, que existia um ciclo, no qual a energia saía do primeiro modo de vibração, começava a se distribuir nos modos mais baixos, para, por fim, voltar quase que inteiramente para o primeiro modo de vibração. Contudo, em 2015, relatou-se que o sistema FPUT poderia atingir equipartição de energia pelo menos entre modos normais livres (interação entre três fônons).
Discretização
A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso [4]. Partimos do problema com correção quadrática, ou seja, . Partindo de:
,
substituímos pelas variáveis discretas:
,
Sendo que as partículas de índice zero e N estão fixas, Chegamos em:
,
Em que é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas.
A Energia do sistema é calculada para cada ciclo de oscilação, porém para obtermos os resultados dos modos de oscilação e compararmos com os estudos atuais e o original de de FPUT, calculamos a energia dos primeiros modos de vibração da corda para demonstrar o comportamento visivelmente periódico destas energias. É possível calcular a energia dos modos de vibração através da equação:
em que é o vetor das posições projetado num vetor de um seno com a frequência do modo que queremos plotar:
e:
é o número de partículas e
Resultados
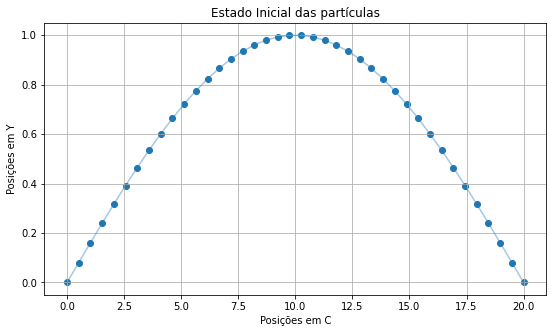
O sistema foi iniciado com o modo normal de oscilação 1 (seno com frequência ), com velocidades iniciais igual a zero de cada partícula. O movimento começa apenas pelas forças já presentes entre cada partículas, pelas equações apresentadas acima.
Segue abaixo a evolução do sistema ao longo do tempo, apenas para gerar o .gif considerando:
Já os resultados das energias, consideramos todas constantes iguais à 1, mais de 100 partículas e o número de iterações está em cada imagem. Procedemos de duas formas: calculamos a porcentagem de cada modo normal de oscilação pela Transformada de Fourier (para selecionar as frequências que estavam presentes na oscilação, sem calcular as energias), o que apresentou um comportamento muito similar às energias calculadas pela soma de energias cinética e potencial:
E também calculamos pela equação de energia citada acima, obtivemos os seguintes comportamentos:
A expressão utilizada para calcular estas energias foi a memsa citada anteriormente:
Discussões
Como o intuito era replicar os resultados e o comportamento das energias através da simulação com dinâmica molecular, obtivemos resultados muito parecidos comparando estudos já realizados sobre este problema [3].
A questão de simular a energia usando a porcentagens dos senos também faz sentido pensando quanta contribuição o modo normal de oscilação tem no movimento atual, como pudemos ver que o comportamento foi bem similar ao das energias calculadas.
Implementação
Implementamos a iteração do movimento das partículas por Velocity-Verlet.
A questão de variar os parâmetros do problema, como já mencionado previamente nesta wiki, e também apresentado nos gráficos e no gif, vimos que não interferia muito no caráter dos resultados (e o quanto isso poderia influenciar no paradoxo de equipartição de energia), porém o fizemos para gerar imagens melhores e o gif com menos de 2 MB.
### Exemplo da iteração do movimento utilizando forcacom correção quadrática ###
### código em python
def aceleracao(pos,alpha,k,massa):
size = len(pos)
acel = [0.0 for i in range(size)]
for i in range(1,size-1):
acel[i] = (k/massa) * ((pos[i+1] + pos[i-1] - 2*pos[i]) * ( 1.0 + alpha*(pos[i+1]-pos[i-1]) ) )
return acel
def velocidade(velo, acel, dt):
size = len(velo)
new_velo = [0.0 for i in range(size)]
for i in range(size):
new_velo[i] = velo[i] + 0.5*acel[i]*dt
return new_velo
def posicao(pos, velo, dt):
size = len(pos)
new_posY = [0.0 for i in range(size)]
for i in range(size):
new_pos[i] = pos[i] + new_velo[i]*dt
return new_pos
N = número de partículas
dt = 0.2
x = np.linspace(0, x_final, dt)
pos = np.sin( 2*x*pi / (N*dt))
while t < tmax: # Loop temporal
plt.scatter(x,pos) # plotagem dos gráficos
acel = aceleracao(pos_old,alpha,k,massa)
velo = velocidade(veloY, new_aceY,dt)
pos = posicao(posY_old, veloY, dt)
calcula_energias(pos)
pos_old = pos.copy() #sem ".copy()" o python usa o mesmo endereço de memória para 2 variáveis
t = t + td
gera_gif()
Link para Códigos
Fizemos no ambiente Colab em .ipynb, segue link do github:[1]
Referências
- ↑ ANDRADE, D. X.; ANJOS, P. H. R.; ASSIS, P. E. G.. Sobre a conexão entre alguns modelos físicos não-lineares. Rev. Bras. Ensino Fís., São Paulo , v. 39, n. 1, e1307, 2017 . Disponível em <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172017000100407&lng=pt&nrm=iso>. http://dx.doi.org/10.1590/1806-9126-rbef-2016-0083.
- ↑ 2,0 2,1 http://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf - Fermi, Pasta, Ulam, Studies of non linear problems Erro de citação: Etiqueta inválida
<ref>; Nome "FPU" definido várias vezes com conteúdo diferente - ↑ 3,0 3,1 https://www.scielo.br/j/rbef/a/SkRCy5fdnGbhfxNjpx5BkRD/?format=pdf&lang=pt - O problema Fermi-Pasta-Ulam-Tsingou: Equiparticão de energia vista através de simulações computacionais
- ↑ https://en.wikipedia.org/wiki/Fermi%E2%80%93Pasta%E2%80%93Ulam%E2%80%93Tsingou_problem









![{\displaystyle m{\ddot {x_{j}}}=k\left(x_{j+1}-2x_{j}+x_{j-1}\right)\left[1+\alpha \left(x_{j+1}-x_{j-1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3059ec0ad9ff614c3283f6a55b74997ffd2a83de)