Motility-Induced Phase Separation(MIPS): mudanças entre as edições
Sem resumo de edição |
|||
| Linha 53: | Linha 53: | ||
</center> | </center> | ||
Onde <math> N_\mathbf{R} = \sum_j A_{\mathbf{R}}^{\theta_i}</math>. A equação (2b), diz respeito ao termo de transição entre uma posição <math> \mathbf{R} </math> e uma posição <math> \mathbf{R}+\mathbf{e}_{\theta_i} </math> na rede hexagonal | |||
==Implementação== | ==Implementação== | ||
Edição das 22h14min de 30 de novembro de 2021
Grupo: Bernardo Boatini e Murilo Kessler Azambuja
Introdução
A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas (Como bio-polímeros que se auto organizam, tipo os microtúbulos que são parte do citoesqueleto celular, ou cardumes de peixe, por exemplo), ou os chamados MIPS (Motility-Induced Phase Separation) que são sistemas que apresentam uma mudança de fase física devido à interações que proíbem a ocupação simultânea de um volume do espaço por duas partículas simultâneas. Nestes sistemas, os agentes possuem a capacidede de auto-propulsão, de forma que a condição de balanço detalhado é quebrada no nível microscópico, uma vez que as partículas possuem uma direção preferencial de movimento.Estes tipos de sistema muitas vezes podem ser tratados a partir de uma abordagem hidrodinâmica, na qual são chamados de fluidos ativos, e divergem do comportamento usual de fluidos compostos de matéria usual inativa, os quais são descritos pela equação de Navier-Stokes.
Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles de de sistemas em equilíbrio. A investigação de comportamentos universais nestes tipos de sistema, além de ser um interece central na física, também pode nos permitir utilizar conhecimentos já bem conhecidos (como a transição de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever sistemas novos. Neste trabalho foi reproduzido o artigo [1] onde foi investigada o comportamento crítico de um sistema com MIPS e se viu que este tipo de sistema pertence à classe de universalidade de sistemas em equilíbrio como o modelo de Ising para spin. Para tal, foi utilizada três abordagens diferentes: um modelo hidrodinâmico, uma descrição baseada em teoria de campos e a simulação de um modelo de rede hexagonal.
Modelo
O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio (FIG. 1).
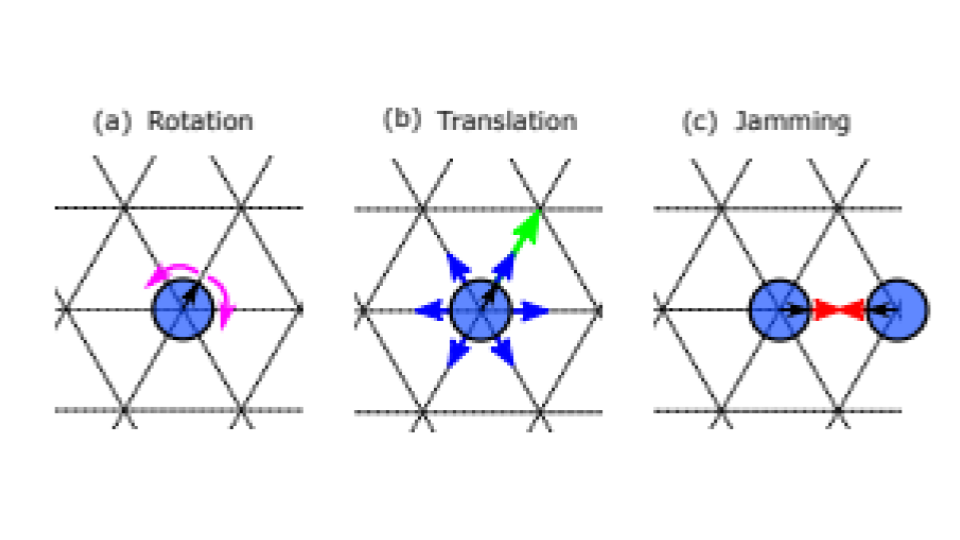
Uma forma de modelar este sistema é considerá-lo um fluido ativo polar e compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. Tal sistema é descrito de forma contínua pela chamada equação de Toner-Tu.
De um ponto de vista microscópico, podemos usar uma formulação discreta baseada na teoria de campos. Neste caso, consideramos uma rede hexagonal bidimensional, com o numero de ocupação de cada sítio da rede restringido por uma constante (futuramente diremos que , de forma que apenas uma partícula pode ocupar cada sítio).
Modelo no Continuo
As equações de Tuner-Tu são dadas por [1]
Onde é o campo de densidade de massa e é o campo de densidade de momentum. A equação (1a) diz respeito à conservação de massa do sistema como um todo. A equação (1b) se assemelha muito à equação de Navier-Stokes, assim podemos ver que o primeiro termo da equação caracteriza a compressibilidade do fluido, o segundo termo representa uma difusão do campo de momentum (o sinal negativo indica que o campo de momentum diminui com o passar do tempo), o terceiro termo representa a viscosidade do fluido e é um ruído Gaussiano com estatísticas espaço-temporais dadas por
onde é a intensidade do ruído.
Modelo no Discreto
Como já foi dito antes, no modelo discreto é utilizado uma rede bidimensional hexagonal com número de ocupação máximo para cada sítio da rede. Os agentes são divididos em seis tipos distintos de partículas ativas, cada uma se move em uma direção (as diagonais do hexágono) e somente vai saltar para o sítio adjacente ao longo desta direção, com uma taxa que depende da ocupação do sítio em questão. Além disso, é possível que uma partícula se transforme em outra, com uma taxa , correspondendo assim a um ruído rotacional de cada partícula. Utilizando a notação utilizada em [1], temos que a rede hexagonal é caracterizado pelo conjunto de vetores e a orientação ou tipo da partícula ativa pelo índice . Desta forma o número de partículas do tipo ocupando o sítio da rede é denotado por . Com o formalismo desenvolvido em [2], temos que a teoria de campos nos fornece para o modelo uma ação dada por
Onde . A equação (2b), diz respeito ao termo de transição entre uma posição e uma posição na rede hexagonal
Implementação
Nessa secção serão colocados alguns detalhes da implementação da rede, das medidas e da dinâmica de Monte Carlo.
Algoritmo
A dinâmica de Monte Carlo foi implementada de forma que a cada MCS, N partículas do sistema são selecionadas aleatoriamente:
- Primeiramente a partícula decide se vai mudar seu sentido() sorteando um valor através de uma distribuição gaussiana centrada em 0, com variância igula a intencidade do ruído ;
- A nova direção é dada por Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \theta + d.60°} ;
- Depois disso a partícula tem probabilidade de andar para o sitio vizinho naquela direção(se ele estiver vazio);
- Caso a partícula não decida andar naquela direção, ela se desloca na direção de outro sitio vizinho(se ele estiver vazio) sorteado aleatoriamente(emulando o comportamento difusivo).
Redes Hexagonais
Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade ao invés de quatro.
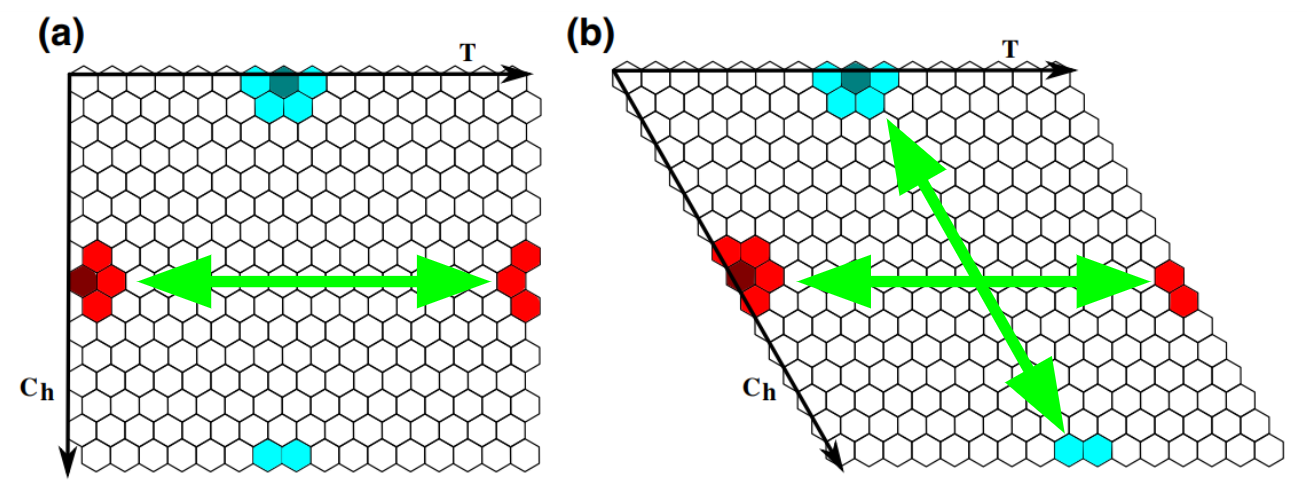
Existem duas topologias possíveis em uma rede hexagonal: "zigzag" e "armchair"[3], e a diferença das duas está principalmente na implementação das condições de contorno periódicas. No caso da topologia em "zigzag"(FIG.2a), o espaço é representado em um paralelogramo, e existem 4 sentidos em que cruzando uma parede a partícula fecha sua trajetória sem ter que cruzar nova mente outra parede do sistema. Na topologia "armchair"(FIG.2b) por outro lado só existem 2 sentidos em que isso acontece.
Sub-Box Sampling Method
O método das subcaixas consiste em dividir o sistema em uma certa quantidade de subsistemas de interesse, permitindo observar a flutuação de densidades apenas nessas regiões.
Nesse trabalho o sistema foi dividido em 4 caixas de tamanho : 2 centradas no centro de massa horizontal do sistema e duas centradas na região horizontal "mais rarefeita", que consequentemente esta a uma distancia de do centro de massa.
Quando os parâmetros permitem que haja separação de fase, duas subcaixas ficam posicionadas exatamente sobre o centro da fase liquida e a mesma coisa para a fase gasosa, permitindo uma medição mais precisa das flutuações de densidade sem considerar as regiões de fronteira.
Porém, essas flutuações se tornam especialmente relevantes no ponto crítico, onde o uso de subcaixas se torna especialmente importante na extração medidas para classificar a transição de fase do modelo em analise.
Medida 1
A primeira medida utilizada para comparar o MIPS com o Ising foi a incompressibilidade isotérmica dos subsistemas definida da seguinte forma
onde denota a média do número de partículas contidas em um subsistema de tamanho L.
(explicar com qual expoente se relaciona e como calcular o erro)
Medida 2
Explicar a medida 2
Resultados
Mostrar e explicar os Resultados
Referência
- ↑ 1,0 1,1 1,2 1,3 https://arxiv.org/pdf/1810.06112.pdf Benjamin Partridge, Chiu Fan Lee, "CRITICAL MOTILITY-INDUCED PHASE SEPARATION BELONGS TO THE ISING UNIVERSALITY CLASS"
- ↑ Disponível em: https://arxiv.org/pdf/0709.1325.pdf Alexandre Lefèvre, Giulio Biroli, "DYNAMICS OF INTERACTING PARTICLE SYSTEMS: STOCHASTIC PROCESS AND FIELD THEORY"
- ↑ 3,0 3,1 HATZIKIROU, Haralambos et al. Extracting cellular automaton rules from physical Langevin equation models for single and collective cell migration. Journal of Mathematical Biology, [s. l.], 2017.















![{\displaystyle -\gamma {\Big (}M-N_{\mathbf {R} +\mathbf {e} _{\theta _{i}}}{\Big )}A_{\mathbf {R} }^{\theta _{i}}{\Big (}e^{{\hat {A}}_{\mathbf {R} +\mathbf {e} _{\theta _{i}}}^{\theta _{i}}-{\hat {A}}_{\mathbf {R} }^{\theta _{i}}}-1{\Big )}{\Bigg ]}\qquad (2b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a905f0ff5b60800cd05104bac165ba402afd46bf)










