Motility-Induced Phase Separation(MIPS): mudanças entre as edições
(→Modelo) |
|||
| Linha 9: | Linha 9: | ||
==Modelo== | ==Modelo== | ||
O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio ( | O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio (FIG. 1). | ||
[[Arquivo: foto.png|thumb|upright=4|none|alt=Alt text|Imagem retirada de (COLOCAR A REFERÊNCIA). Em (a) vemos a difusão devido à rotação da direção de movimento preferencial da partícula, em (b) temos o "movimento balístico" (seta verde) e a difusão devido à translação da partícula (setas azuis) e, em (c), vemos a interação entre partículas em sítios vizinhos, impedindo a ocupação simultânea do mesmo sítio por duas partículas.]] | [[Arquivo: foto.png|thumb|upright=4|none|alt=Alt text|FIGURA 1: Imagem retirada de (COLOCAR A REFERÊNCIA). Em (a) vemos a difusão devido à rotação da direção de movimento preferencial da partícula, em (b) temos o "movimento balístico" (seta verde) e a difusão devido à translação da partícula (setas azuis) e, em (c), vemos a interação entre partículas em sítios vizinhos, impedindo a ocupação simultânea do mesmo sítio por duas partículas.]] | ||
Uma forma de modelar este sistema é considerá-lo um fluido ativo compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. | |||
Explicar as propriedades do tipo de fluido que se espera | Explicar as propriedades do tipo de fluido que se espera | ||
Edição das 16h52min de 28 de novembro de 2021
Grupo: Bernardo Boatini e Murilo Kessler Azambuja
Introdução
A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas (Como bio-polímeros que se auto organizam, tipo os microtúbulos que são parte do citoesqueleto celular, ou cardumes de peixe, por exemplo), ou os chamados MIPS (Motility-Induced Phase Separation) que são sistemas que apresentam uma mudança de fase física devido à interações que proíbem a ocupação simultânea de um volume do espaço por duas partículas simultâneas. Nestes sistemas, os agentes possuem a capacidede de auto-propulsão, de forma que a condição de balnço detalhado é quebrada no nível microscópico, uma vez que as partículas possuem uma direção preferencial de movimento.Estes tipos de sistema muitas vezes podem ser tratados a partir de uma abordagem hidrodinâmica, na qual são chamados de fluidos ativos, e divergem do comportamento usual de fluidos compostos de matéria usual inativa, os quais são descritos pela equação de Navier-Stokes.
Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles de de sistemas em equilíbrio. A investigação de comportamentos universais nestes tipos de sistema, além de ser um interece central na física, também pode nos permitir utilizar conhecimentos já bem conhecidos (como a transição de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever sistemas novos. Neste trabalho foi reproduzido o artigo (COLOCAR A REFERÊNCIA) onde foi investigada o comportamento crítico de um sistema com MIPS e se viu que este tipo de sistema pertence à classe de universalidade de sistemas em equilíbrio como o modelo de Ising para spin. Para tal, foi utilizada três abordagens diferentes: um modelo hidrodinâmico, uma descrição baseada em teoria de campos e a simulação de um modelo de rede hexagonal.
Modelo
O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio (FIG. 1).
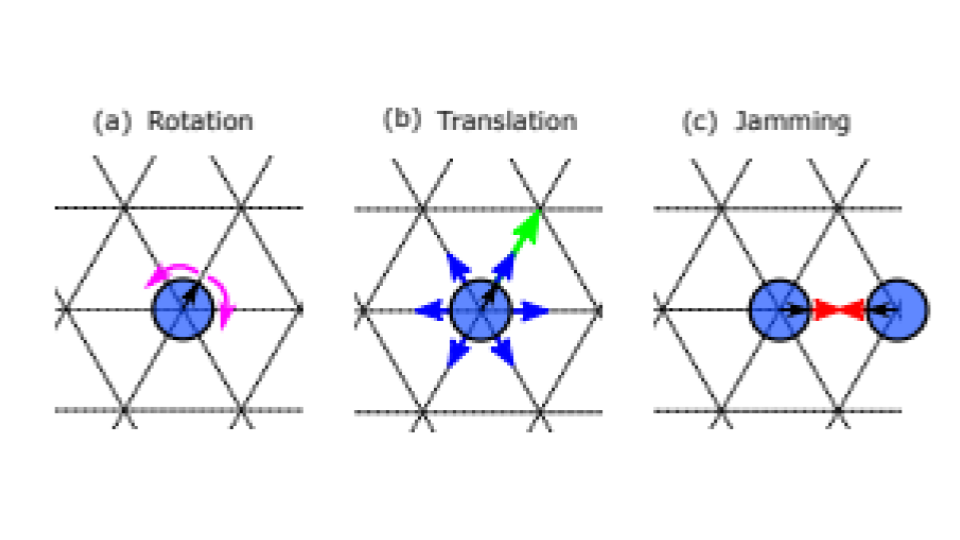
Uma forma de modelar este sistema é considerá-lo um fluido ativo compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos.
Explicar as propriedades do tipo de fluido que se espera
Modelo no Continuo
Mostrar e explicar a equação de Toner-Tu
Modelo no Discreto
Mostrar e explicar(ou falar por cima) da abordagem de campo discreto
Implementação
Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade.
Sub-Box Sampling Method
Explicar o método das sub caixas
Medida 1
Explicar a medida 1
Medida 2
Explicar a medida 2
Resultados
Mostrar e explicar os Resultados