Modelos Epidemiológicos: mudanças entre as edições
| Linha 94: | Linha 94: | ||
'''Modelo 1''' | '''Modelo 1''' | ||
<source lang='c'> | |||
void jogo(int t){ | |||
/* | |||
Dinâmica da escolha voluntária do quarentenado ou não | |||
*/ | |||
int sitio, i, j, k; | |||
double prob; | |||
double sums, sumv; | |||
int vizinho, dir; | |||
for (i=0;i<L2;i++){ | |||
sitio = FRANDOM * L2; | |||
dir = FRANDOM * 4 + 1; | |||
vizinho = viz[sitio][dir]; | |||
sums = 0; | |||
sumv = 0; | |||
for(j=1 ; j < 5 ; j++) { | |||
sums += payoff[dmc_quarentena[sitio]][dmc_quarentena[viz[sitio][j]]]; | |||
sumv += payoff[dmc_quarentena[vizinho]][dmc_quarentena[viz[vizinho][j]]]; | |||
} | |||
prob = 1.0 / (1.0 + exp(-(sumv - sums) / TEMP )); | |||
if(FRANDOM > prob) { | |||
dmc_quarentena[sitio] = dmc_quarentena[vizinho]; | |||
} | |||
} | |||
// Escreve no arquivo o estado de cada um, linha = tempo | |||
FILE *dmcfile; | |||
char output2[10000]; | |||
sprintf(output2, "output_dinamica_loc.txt"); | |||
dmcfile = fopen(output2,"a"); | |||
for(k=0; k<L2; k++){ | |||
fprintf(dmcfile," %d ", dmc_quarentena[k]); | |||
} | |||
fprintf(dmcfile," \n "); | |||
fclose(dmcfile); | |||
return; | |||
} | |||
</source> | |||
Edição das 17h05min de 22 de novembro de 2021
Em construção
Grupo: Gabriel Schmökel, Julia Remus e Luis Gustavo Lang Gaiato
O objetivo do trabalho é realizar a implementação do modelo SIR e de dois modelos simplificados do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" [1] utilizando Monte Carlo.
Será apresentada uma breve introdução sobre o tema e as equações que envolvem o desenvolvimento dos cálculos, as implementações e seus respectivos resultados. Os códigos foram realizados na linguagem C.
Introdução
O objetivo do trabalho é realizar a implementação do modelo SIR e de dois modelos simplificados do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" [1] utilizando Monte Carlo e linguagem C.
Os dois modelos simplificados propostos são:
- Modelo 1: cada indivíduo escolha a quarentena ou não dependendo somente se os seus vizinhos estão quarentenados
- Modelo 2: o indivíduo escolhe se quarentenar se os seus vizinhos estão infectados, ainda não consegue diferenciar os indivíduos recuperados e suscetíveis
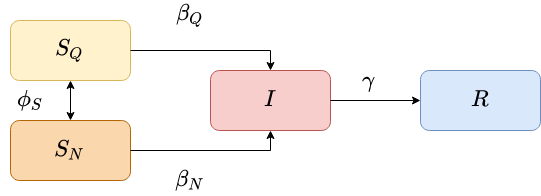
O esquemático do modelo SIR com a escolha da quarentena pode ser visto na seção Modelo SIR com quarentena voluntária.
Modelo SIR
Esse modelo propõe dividir a população em três categorias:
- Susceptível (S): um componente susceptível é aquele que ainda não passou e não possui a doença, mas poderá ser infectado em contato com I
- Infectado (I): um componente infectado com a doença
- Recuperado ou Removido (R): aquele que já passou pela doença e já está recuperado dela com imunidade (não pegará novamente); pode ser utilizado o compartimento como sendo de removidos, com o cuidado de retirá-los do modelo
Modelo SIR com quarentena voluntária
No esquemático pode-se ver o modelo utilizado no trabalho, ele é uma simplificação do artigo escrito por Amaral, et al [1]. Nele temos:
- Componentes suscetíveis podem estar ou não em quarentena. A probabilidade para a escolha da quarentena ocorrer depende de quantos infectados há nos vizinhos.
- Ao escolher estar ou não em quarentena, esses componentes tem probabilidades diferentes de adquirir a doença ( e ) e se tornar infectados.
- Infectados possuem a mesma probabilidade de se tornarem recuperados.
- Após recuperados da doença, as pessoas não conseguem adquiri-lá novamente.
Para simular a quarentena voluntária é utilizado o jogo definido pelo Dilema do Prisioneiro. Esse dilema descreve a situação onde dois condenados (A e B) precisam decidir se colaboram ou não sem saber a decisão do seu par. Para isso temos 4 possibilidades: A e B colaboram (ambos saem com uma recompensa R), A colabora mas B não colabora (B ficaria com o valor da tentação T e A com o custo do sonso S), o caso contrário onde A não colabora e B colabora e A e B não colaboram (ambos ganham com uma penalidade P). [2]
Essas possibilidades podem ser resumidas em uma matriz de perdas e ganhos (matriz de payoff):
| A coopera | A não coopera | |
|---|---|---|
| B coopera | R / R | S / T |
| B não coopera | T / S | P / P |
Os valores da matriz payoff devem obedecer a ordem T > R > P > S. Além disso, para simulações com várias iterações deve ser obedecido que 2R > T + S. [2]
A proposta de observar a evolução da infecção dependendo da quarentena precisa utilizar mais de um par de interagentes, por isso é definido uma rede onde cada componente possui um ponto fixo. A partir disso, cada um desses componentes interagem com seus quatro vizinhos mais próximos (para os pontos do contorno é utilizado que as bordas são unidas por condições de contorno periódicas). [2]
Segundo Hauert e Szabó [2], os colaboradores tendem a ser extintos em jogos que consideram a interação aleatória, independente da sua concentração inicial, ou seja, todos tendem a não ganhar nada (não colaborar mutuamente) a fim de reduzir custos. Enquanto isso, se for proposto que um componente só escolhe uma estratégia conforme seus vizinhos, é visto é a formação de clusters de cooperadores e de não cooperadores; com isso, os componentes que estão na borda desses espaços, ganham na interação com os vizinhos colaboradores e perdem com a outra interação.
Esse jogo de quarentena é acoplado ao sistema SIR anteriormente descrito. A única diferença para o SIR sem o jogo é que as probabilidades de um componente S se tornar infectado mudam a partir do seu estado de quarentena.
No segundo modelo é feita uma simplificação considerando suscetíveis e recuperados como o mesmo estado, desta forma, ambos modelos podem utilizar a matriz de payoff como apresentada.
Implementação modelo SIR
Talvezzzz: Usar essa Analytical solution of SIR-model [3] pra verificar se o código funciona
Implementação modelo SIR com quarentena voluntária
Algumas modificações são realizadas no código anterior: a probabilidade do indivíduo passar de suscetível a infectado depende da escolha pela quarentena e é adicionada a parte da escolha individual.
Modelo 1
void jogo(int t){
/*
Dinâmica da escolha voluntária do quarentenado ou não
*/
int sitio, i, j, k;
double prob;
double sums, sumv;
int vizinho, dir;
for (i=0;i<L2;i++){
sitio = FRANDOM * L2;
dir = FRANDOM * 4 + 1;
vizinho = viz[sitio][dir];
sums = 0;
sumv = 0;
for(j=1 ; j < 5 ; j++) {
sums += payoff[dmc_quarentena[sitio]][dmc_quarentena[viz[sitio][j]]];
sumv += payoff[dmc_quarentena[vizinho]][dmc_quarentena[viz[vizinho][j]]];
}
prob = 1.0 / (1.0 + exp(-(sumv - sums) / TEMP ));
if(FRANDOM > prob) {
dmc_quarentena[sitio] = dmc_quarentena[vizinho];
}
}
// Escreve no arquivo o estado de cada um, linha = tempo
FILE *dmcfile;
char output2[10000];
sprintf(output2, "output_dinamica_loc.txt");
dmcfile = fopen(output2,"a");
for(k=0; k<L2; k++){
fprintf(dmcfile," %d ", dmc_quarentena[k]);
}
fprintf(dmcfile," \n ");
fclose(dmcfile);
return;
}
Modelo 2
Resultados
Referências
- ↑ 1,0 1,1 1,2 AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. arXiv:2008.05979v2 [physics.soc-ph] .
- ↑ 2,0 2,1 2,2 2,3 HAUERT, Christoph; SZABÓ, György. Game theory and physics. DOI: 10.1119/1.18485144 .
- ↑ Analytical solution of SIR-model