Modelo de Levins aprimorado para 2 espécies II: mudanças entre as edições
(Criou página com '{{Ecologia| Modelo de Levins aprimorado para 2 espécies I |Modelo espacialmente explícito para 2 espécies}} {{Ecolog...') |
Sem resumo de edição |
||
| (Uma revisão intermediária pelo mesmo usuário não está sendo mostrada) | |||
| Linha 1: | Linha 1: | ||
{{Ecologia| [[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]] |[[Modelo espacialmente explícito para 2 espécies]]}} | {{Ecologia| [[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]] |[[Modelo espacialmente explícito para 2 espécies]]}} | ||
===Original=== | |||
O artigo ''Waves of desertification in a competitive ecosystem'' propõe o seguinte modelo de campo médio para representar o mesmo contexto ecológico discutido no [[Modelo espacialmente explícito para 2 espécies]]:<math display="block">\begin{align} | |||
\dot{x}_{1} & =c_{1}\left(h-x_{1}\right)x_{1}-e_{1}x_{1}\end{align}</math><math display="block">\begin{align} | |||
\dot{x}_{2} & =c_{2}\left(h-x_{1}-x_{2}\right)x_{2}-e_{2}x_{2}\end{align}</math><math display="block">\dot{h}=-\gamma x_{2}\left(t-\tau_{0}\right)h\left(t-\tau_{0}\right)+\gamma x_{2}\left(t-\tau_{0}-\tau_{r}\right)h\left(t-\tau_{0}-\tau_{r}\right)</math> | |||
Denotando a equação com atraso <math display="inline">f_{\tau}\left(t-\tau\right)</math> e sendo <math display="inline">\tau=\tau_{0}+\tau_{r}</math> então ainda podemos reescrever a última equação como: | |||
<math display="block">\dot{h}=-\gamma x_{2\tau_{0}}h_{\tau_{0}}+\gamma x_{2\tau}h_{\tau}</math> | |||
Podemos ver que há 2 termos para a dinâmica dos fragmentos disponíveis. Onde <math display="inline">\tau_{0}</math> é o tempo que um fragmento ocupado leva para ser deteriorado, por isso o primeiro termo busca quantificar os fragmentos <math display="inline">h\left(t\right)</math> que estavam ocupados pela espécie <math display="inline">x\left(t\right)</math> em um tempo <math display="inline">\tau_{0}</math> anterior, deste modo, no instante <math display="inline">t</math> estes fragmentos se deterioram representando uma decréscimo nos fragmentos disponíveis. De maneira análoga, o segundo termo busca os fragmentos que estavam ocupados em um instante <math display="inline">\tau=\tau_{0}+\tau_{r}</math> anterior, pois passado <math display="inline">\tau_{r}</math> após a deterioração, o fragmento se recupera e representa um aumento nos fragmentos disponíveis. | |||
Considerando que no ponto de equilíbrio temos <math display="inline">f=f_{\tau}=f_{\tau_{0}}</math> , logo obtém-se <math display="inline">\dot{h}=0</math>. Pois o mesmo fragmento que é deteriorado em um instante <math display="inline">t+\tau_{0}</math> é recuperado em um instante posterior <math display="inline">t+\tau_{0}+\tau_{r}</math>. Sendo assim, o ponto de equilíbrio final irá depender da fração <math display="inline">h\left(t\right)=h_{c}</math> no momento em que o equilíbrio é atingido. Porém qual é exatamente este valor <math display="inline">h\left(t\right)=h_{c}</math> não parece ser possível de ser obtido de maneira analítica. Considerando um termo constante arbitrário <math display="inline">h_{c}=h</math> no equilíbrio tem-se <math>\dot{x}=0 | |||
</math>, então o sistema reduz-se a: | |||
<math display="block">\begin{align} | |||
0= & c_{1}\left(h-x_{1}\right)x_{1}-e_{1}x_{1}\\ | |||
0= & c_{2}\left(h-x_{1}-x_{2}\right)x_{2}-e_{2}x_{2}\end{align}</math> | |||
Esse sistema possui 4 soluções possíveis: | |||
*<math display="inline">\left(0,0\right)\rightarrow</math> Nenhum animal sobrevive | |||
*<math display="inline">\left(h-\frac{e_{1}}{c_{1}},0\right)\rightarrow</math>Apenas guanacos sobrevivem | |||
*<math display="inline">\left(0,h-\frac{e_{2}}{c_{2}}\right)\rightarrow</math> Apenas ovelhas sobrevivem | |||
*<math display="inline">\left(h-\frac{e_{1}}{c_{1}},\frac{e_{1}}{c_{1}}-\frac{e_{2}}{c_{2}}\right)\rightarrow</math> Ambos sobrevivem | |||
Continuando a análise deste conjunto de equações, mas lembrando que <math display="inline">h</math> é um valor que vai ser definido pela evolução do sistema e que não temos ferramentas aqui para prever qual será exatamente o ponto de equilíbrio. Linearizando através da matriz jacobiana, onde denotamos um ponto de equilíbrio qualquer por <math display="inline">\left(x_{1}^{*},x_{2}^{*}\right)</math>: | |||
<math display="block">\left(\begin{array}{c} | |||
\dot{x}_{1}\\ | |||
\dot{x}_{2} | |||
\end{array}\right)=\left.\left(\begin{array}{cc} | |||
-e_{1}+c_{1}\left(h-x_{1}\right)-c_{1}x_{1} & 0\\ | |||
-c_{2}x_{2} & -e_{2}+c_{2}\left(h-x_{1}-x_{2}\right)-c_{2}x_{2} | |||
\end{array}\right)\right|_{\left(x_{1}^{*},x_{2}^{*}\right)}\left(\begin{array}{c} | |||
x_{1}\\ | |||
x_{2} | |||
\end{array}\right)</math> | |||
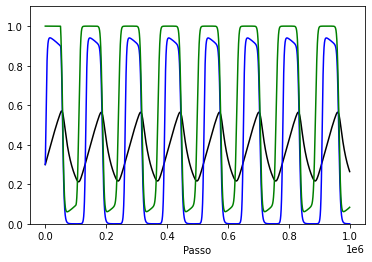
[[Ficheiro:2h1.png|miniaturadaimagem|Solução do sistema de equações diferenciais originalmente proposto para a seguinte condição inicial <math>\left(x_{10},x_{20},h_{0}\right)=\left(0.3,0.3,1.\right)</math>.]] | |||
Com o auxílio do Mathematica e considerando o conjunto de parâmetros definidos originalmente no artigo, temos as seguintes equações características dependendo de <math display="inline">h</math> para cada ponto de equilíbrio: | |||
#<math display="inline">l^{2}+\left(0.066h\right)l+\left(-0.028h^{2}+0.0074h-0.0001\right)=0</math> | |||
#<math display="inline">l^{2}+\left(0.155+0.04h \right)l+\left(0.0066h-0.00165\right)=0</math> | |||
#<math display="inline">l^{2}+\left(0.02-0.74h\right)l+\left(0.028h^{2}-0.0074h+0.0001\right)=0</math> | |||
#<math display="inline">l^{2}+\left(0.04h-0.175\right)l+\left(-0.0066h+0.00165\right)=0</math> | |||
Podemos ver que são polinômios do segundo grau, e lembrando que <math display="inline">h\in\left[0,1\right]</math> é um número real, temos os seguintes autovalores (ou raízes): | |||
#<math display="inline">l=-0.5\left(\sqrt{0.5476h^{2}+0.0004-0.0296h}+0.66h\right)</math> e <math display="inline">l=0.5\left(\sqrt{0.5476h^{2}+0.0004-0.0296h}-0.66h\right)</math> | |||
#<math display="inline">l=-0.5\left(\sqrt{0.0016h^{2}-0.014h+0.030625}+0.04h+0.155\right)</math> e <math display="inline">l=0.5\left(\sqrt{0.0016h^{2}-0.014h+0.030625}-0.04h-0.155\right)</math> | |||
#<math display="inline">l\approx0.04h-0.01</math> e <math display="inline">l\approx0.7-0.01</math> | |||
#<math display="inline">l=0.5\left(0.175-\sqrt{0.0016h^{2}+0.0124h+0.024025}-0.04h\right)</math> e <math display="inline">l=0.5\left(\sqrt{0.0016h^{2}+0.0124h+0.024025}+0.175-0.04h\right)</math> | |||
É importante perceber que as raízes são sempre reais. Então variando <math>h</math>, obtém-se as seguintes situações: | |||
* <math display="inline">h<0.125</math>: Nenhum animal sobrevive | |||
*<math display="inline">0.125<h<0.25</math>: Apenas ovelha sobrevive | |||
*<math display="inline">h>0.25</math>: guanacos e ovelha sobrevivem | |||
Podemos perceber que a condição que apenas o guanaco sobrevive nunca é um ponto de equilíbrio estável. No máximo um ponto de cela, e concordando com os outros modelos discutidos anteriormente, os guanacos são mais sensíveis a destruição do meio ambiente. | |||
*'''Observação''': de certa forma todas essas análise sobre o comportamento do sistema entorno dos pontos de equilíbrio é“inútil”. Pois ela parte do pressuposto de que <math display="inline">h\left(t\right)=h</math> é constante, o que não temos meios de confirmar que corresponde a realidade e nem de identificar qual é o valor, mesmo que seja. | |||
===Modificado=== | |||
Inserindo um termo <math display="inline">x_{1}x_{2}</math> na equação de <math display="inline">\dot{x}_{2}</math> com o mesmo argumento utilizado no [[Modelo de Levins aprimorado para 3 espécies]] baseado em conceitos de probabilidade e teoria dos conjuntos, ficamos com o seguinte sistema: | |||
<math display="block">\begin{align} | |||
\dot{x}_{1} & =c_{1}\left(h-x_{1}\right)x_{1}-e_{1}x_{1}\end{align}</math><math display="block">\begin{align} | |||
\dot{x}_{2} & =c_{2}\left(h-x_{1}-x_{2}+x_{1}x_{2}\right)x_{2}-e_{2}x_{2}\end{align}</math><math display="block">\dot{h}=-\gamma x_{2\tau_{0}}h_{\tau_{0}}+\gamma x_{2\tau}h_{\tau}</math> | |||
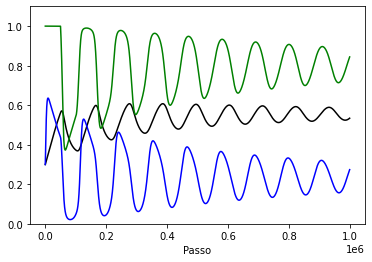
[[Ficheiro:2h2.png|esquerda|miniaturadaimagem|Solução do sistema de equações diferenciais modificadas para a seguinte condição inicial <math>\left(x_{10},x_{20},h_{0}\right)=\left(0.3,0.3,1.\right)</math>.]] | |||
A solução numérica deste sistema considerando as condições iniciais de forma semelhante com o que foi feito no [[Sistemas de equações diferenciais com atrasos fixos - SIRS|SIRS]] revela uma solução oscilatória conforme foi encontrado no [[Modelo espacialmente explícito para 2 espécies|modelo espacialmente]] equivalente. Poderíamos repetir a análise feita para o sistema anterior acerca dos pontos de equilíbrio ou até tentar se aprofundar mais, mas a verdade é que as equações diferenciais com atraso são significativamente mais complexas de serem analisadas que equações diferenciais sem atraso. E não parece que essa camada de complexidade adicional melhore os resultados o suficiente para ser justificado no momento. Conforme destacado não só no artigo no qual este trabalho se baseou, os modelos espacialmente explícitos são ferramentas mais valiosas que o sistemas de equações<ref>[https://arxiv.org/pdf/1409.0024.pdf Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances] (Fabiana Laguna e outros, Ecological Modelling)</ref>, pois se aproximam melhor das situações reais. Sendo assim, não me aprofundarei na análise deste sistema. | |||
=== Códigos === | |||
O código utilizado para a solução dos sistemas de equações diferenciais foi feito em [https://www.python.org/ Python] utilizando o método numérico de Euler: | |||
# Solução do sistema de equações diferenciais com atraso para 2 espécies com dinâmica dos fragmentos disponíveis | |||
# Jhordan Silveira de Borba | |||
# sbjhordan@gmail.com | |||
import numpy as np # Biblioteca para o cálculo científico | |||
#Parâmetros da dinâmica | |||
c1=0.04 | |||
c2=0.7 | |||
e1=0.01 | |||
e2=0.01 | |||
g=0.1 | |||
tr=10 | |||
to=50 | |||
t=tr+to | |||
# Listas para guardar a evolução do sistema | |||
x1=[] | |||
x2=[] | |||
h=[] | |||
d=0.001 #Passo para o método de Euler | |||
#Primeira parte: | |||
N1=int(to/d) #Quantidade de passos | |||
x1.append(0.3) #Condição inicial de guanacos | |||
x2.append(0.3) #Condição inicial de pumas | |||
h.append(1.) #Condição inicial de fragmentos disponíveis | |||
#Resolve o sistema Usando o método de Euler | |||
for k in range(N1): | |||
x1.append(x1[k]+d*(c1*(h[0]-x1[k] )*x1[k]-e1*x1[k])) | |||
x2.append(x2[k]+d*(c2*(h[0]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1)) | |||
h.append(h[0]) | |||
#Segunda parte | |||
N2=int(t/d) | |||
for k in range(N1,N2): | |||
x1.append(x1[k]+d*(c1*(h[k]-x1[k] )*x1[k]-e1*x1[k])) | |||
x2.append(x2[k]+d*(c2*(h[k]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1)) | |||
h.append(h[k]+d*(-g*x2[k-int(to/d)]*h[k-int(to/d)])) | |||
#Terceira parte | |||
N3=int(1000/d) | |||
for k in range(N2,N3): | |||
x1.append(x1[k]+d*(c1*(h[k]-x1[k] )*x1[k]-e1*x1[k])) | |||
x2.append(x2[k]+d*(c2*(h[k]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1)) | |||
h.append(h[k]+d*(-g*x2[k-int(to/d)]*h[k-int(to/d)]+g*x2[k-int(t/d)]*h[k-int(t/d)])) | |||
E o sistema de equações pode ser analisado via [https://www.wolfram.com/mathematica/index.html.pt-br?footer=lang Mathematica] utilizando:<pre> | |||
parametros = {c1 -> 0.04, c2 -> 0.7, e1 -> 0.01, e2 -> 0.01, tr -> 10, | |||
to -> 50, g -> 0.1}; | |||
dx1 = (c1* x1 (h - x1) - e1 x1); | |||
dx2 = (c2 x2 (h - x1 - x2) - e2 x2); | |||
sol = Solve[dx1 == 0 && dx2 == 0, {x1, x2}]; | |||
M = {{D[dx1, x1], D[dx1, x2]}, {D[dx2, x1], D[dx2, x2]}}; | |||
</pre>Onde a análise do ponto de equilíbrio <math>n</math> pode ser obtida por:<pre> | |||
n = 2; | |||
MA = M /. sol[[n]] /. parametros; | |||
P = CharacteristicPolynomial[MA, l] | |||
Roots[P == 0, l] | |||
</pre> | |||
====Principal material utilizado==== | |||
#[https://fisica.cab.cnea.gov.ar/estadistica/abramson/papers/ecological/desertification.pdf Waves of desertification in a competitive ecosystem] (Y. C. Daza C. e outros, Ecological Modelling) | |||
==== Referências==== | |||
<references /> | |||
{{Ecologia| [[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]] |[[Modelo espacialmente explícito para 2 espécies]]}} | {{Ecologia| [[Modelo de Levins aprimorado para 2 espécies | Modelo de Levins aprimorado para 2 espécies I]] |[[Modelo espacialmente explícito para 2 espécies]]}} | ||
Edição atual tal como às 20h37min de 26 de junho de 2021
Anterior: Modelo de Levins aprimorado para 2 espécies I | Índice: Ecologia | Próximo: Modelo espacialmente explícito para 2 espécies
Original
O artigo Waves of desertification in a competitive ecosystem propõe o seguinte modelo de campo médio para representar o mesmo contexto ecológico discutido no Modelo espacialmente explícito para 2 espécies:
Denotando a equação com atraso e sendo então ainda podemos reescrever a última equação como:
Podemos ver que há 2 termos para a dinâmica dos fragmentos disponíveis. Onde é o tempo que um fragmento ocupado leva para ser deteriorado, por isso o primeiro termo busca quantificar os fragmentos que estavam ocupados pela espécie em um tempo anterior, deste modo, no instante estes fragmentos se deterioram representando uma decréscimo nos fragmentos disponíveis. De maneira análoga, o segundo termo busca os fragmentos que estavam ocupados em um instante anterior, pois passado após a deterioração, o fragmento se recupera e representa um aumento nos fragmentos disponíveis.
Considerando que no ponto de equilíbrio temos , logo obtém-se . Pois o mesmo fragmento que é deteriorado em um instante é recuperado em um instante posterior . Sendo assim, o ponto de equilíbrio final irá depender da fração no momento em que o equilíbrio é atingido. Porém qual é exatamente este valor não parece ser possível de ser obtido de maneira analítica. Considerando um termo constante arbitrário no equilíbrio tem-se , então o sistema reduz-se a:
Esse sistema possui 4 soluções possíveis:
- Nenhum animal sobrevive
- Apenas guanacos sobrevivem
- Apenas ovelhas sobrevivem
- Ambos sobrevivem
Continuando a análise deste conjunto de equações, mas lembrando que é um valor que vai ser definido pela evolução do sistema e que não temos ferramentas aqui para prever qual será exatamente o ponto de equilíbrio. Linearizando através da matriz jacobiana, onde denotamos um ponto de equilíbrio qualquer por :
Com o auxílio do Mathematica e considerando o conjunto de parâmetros definidos originalmente no artigo, temos as seguintes equações características dependendo de para cada ponto de equilíbrio:
Podemos ver que são polinômios do segundo grau, e lembrando que é um número real, temos os seguintes autovalores (ou raízes):
- e
- e
- e
- e
É importante perceber que as raízes são sempre reais. Então variando , obtém-se as seguintes situações:
- : Nenhum animal sobrevive
- : Apenas ovelha sobrevive
- : guanacos e ovelha sobrevivem
Podemos perceber que a condição que apenas o guanaco sobrevive nunca é um ponto de equilíbrio estável. No máximo um ponto de cela, e concordando com os outros modelos discutidos anteriormente, os guanacos são mais sensíveis a destruição do meio ambiente.
- Observação: de certa forma todas essas análise sobre o comportamento do sistema entorno dos pontos de equilíbrio é“inútil”. Pois ela parte do pressuposto de que é constante, o que não temos meios de confirmar que corresponde a realidade e nem de identificar qual é o valor, mesmo que seja.
Modificado
Inserindo um termo na equação de com o mesmo argumento utilizado no Modelo de Levins aprimorado para 3 espécies baseado em conceitos de probabilidade e teoria dos conjuntos, ficamos com o seguinte sistema:
A solução numérica deste sistema considerando as condições iniciais de forma semelhante com o que foi feito no SIRS revela uma solução oscilatória conforme foi encontrado no modelo espacialmente equivalente. Poderíamos repetir a análise feita para o sistema anterior acerca dos pontos de equilíbrio ou até tentar se aprofundar mais, mas a verdade é que as equações diferenciais com atraso são significativamente mais complexas de serem analisadas que equações diferenciais sem atraso. E não parece que essa camada de complexidade adicional melhore os resultados o suficiente para ser justificado no momento. Conforme destacado não só no artigo no qual este trabalho se baseou, os modelos espacialmente explícitos são ferramentas mais valiosas que o sistemas de equações[1], pois se aproximam melhor das situações reais. Sendo assim, não me aprofundarei na análise deste sistema.
Códigos
O código utilizado para a solução dos sistemas de equações diferenciais foi feito em Python utilizando o método numérico de Euler:
# Solução do sistema de equações diferenciais com atraso para 2 espécies com dinâmica dos fragmentos disponíveis
# Jhordan Silveira de Borba
# sbjhordan@gmail.com
import numpy as np # Biblioteca para o cálculo científico
#Parâmetros da dinâmica
c1=0.04
c2=0.7
e1=0.01
e2=0.01
g=0.1
tr=10
to=50
t=tr+to
# Listas para guardar a evolução do sistema
x1=[]
x2=[]
h=[]
d=0.001 #Passo para o método de Euler
#Primeira parte:
N1=int(to/d) #Quantidade de passos
x1.append(0.3) #Condição inicial de guanacos
x2.append(0.3) #Condição inicial de pumas
h.append(1.) #Condição inicial de fragmentos disponíveis
#Resolve o sistema Usando o método de Euler
for k in range(N1):
x1.append(x1[k]+d*(c1*(h[0]-x1[k] )*x1[k]-e1*x1[k]))
x2.append(x2[k]+d*(c2*(h[0]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1))
h.append(h[0])
#Segunda parte
N2=int(t/d)
for k in range(N1,N2):
x1.append(x1[k]+d*(c1*(h[k]-x1[k] )*x1[k]-e1*x1[k]))
x2.append(x2[k]+d*(c2*(h[k]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1))
h.append(h[k]+d*(-g*x2[k-int(to/d)]*h[k-int(to/d)]))
#Terceira parte
N3=int(1000/d)
for k in range(N2,N3):
x1.append(x1[k]+d*(c1*(h[k]-x1[k] )*x1[k]-e1*x1[k]))
x2.append(x2[k]+d*(c2*(h[k]-x1[k]-x2[k]+x1[k]*x2[k])*x2[k]-e2*x2[k]-x1[k]*x2[k]*c1))
h.append(h[k]+d*(-g*x2[k-int(to/d)]*h[k-int(to/d)]+g*x2[k-int(t/d)]*h[k-int(t/d)]))
E o sistema de equações pode ser analisado via Mathematica utilizando:
parametros = {c1 -> 0.04, c2 -> 0.7, e1 -> 0.01, e2 -> 0.01, tr -> 10,
to -> 50, g -> 0.1};
dx1 = (c1* x1 (h - x1) - e1 x1);
dx2 = (c2 x2 (h - x1 - x2) - e2 x2);
sol = Solve[dx1 == 0 && dx2 == 0, {x1, x2}];
M = {{D[dx1, x1], D[dx1, x2]}, {D[dx2, x1], D[dx2, x2]}};
Onde a análise do ponto de equilíbrio pode ser obtida por:
n = 2; MA = M /. sol[[n]] /. parametros; P = CharacteristicPolynomial[MA, l] Roots[P == 0, l]
Principal material utilizado
- Waves of desertification in a competitive ecosystem (Y. C. Daza C. e outros, Ecological Modelling)
Referências
- ↑ Mathematical model of livestock and wildlife: Predationand competition under environmental disturbances (Fabiana Laguna e outros, Ecological Modelling)
Anterior: Modelo de Levins aprimorado para 2 espécies I | Índice: Ecologia | Próximo: Modelo espacialmente explícito para 2 espécies































![{\textstyle h\in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58749d78ea4a06f198258d35c84e908ffb9a35dc)