Modelo de Fitzhugh-Nagumo para o potencial de ação em neurônios: mudanças entre as edições
| Linha 365: | Linha 365: | ||
<math>\frac{\partial w}{\partial t} = \epsilon\left(v - \gamma w\right) </math> | <math>\frac{\partial w}{\partial t} = \epsilon\left(v - \gamma w\right) </math> | ||
Lembrando que nesse formato assumimos <math>I = 0</math> pois os estímulos não serão constantes no tempo, serão dados na condição inicial. | |||
Como a equação de recuperação já foi discretizada, e não depende da dimensão do problema, precisamos apenas aplicar o FTCS na equação de Nagumo em 2D. Assumindo <math>\Delta x = \Delta y</math>, temos | Como a equação de recuperação já foi discretizada, e não depende da dimensão do problema, precisamos apenas aplicar o FTCS na equação de Nagumo em 2D. Assumindo <math>\Delta x = \Delta y</math>, temos | ||
Edição das 10h42min de 7 de abril de 2021
Grupo: Bernardo Boatini, Murilo Kessler Azambuja e Natália Ferrazzo
O objetivo deste trabalho é implementar e estudar a dinâmica do modelo Fitzhugh-Nagumo para potenciais de ação em células e tecidos excitáveis. O método computacional utilizado para resolver os problemas e implementar o modelo foi o FTCS (Forward Time Centered Space) e o método de Crank-Nicolson.
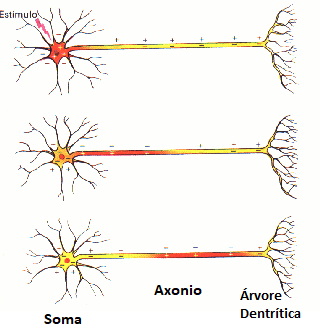
Potencial de Ação em Neurônios
A células vivas são sistemas eletricamente sensíveis, ou seja, podem reagir a estímulos elétricos. Isso se dá devido ao fato de que substâncias carregadas estão naturalmente vinculadas a seus processos internos de interação com o ambiente, principalmente por intermédio de canais iônicos e proteínas transmebrana como, por exemplo, a Bomba de Sódio e Potássio (Bomba Na⁺/K⁺ ATPase)[1].
Naturalmente todas as células vivas possuem um potencial de repouso (PR) elétrico, ou seja, uma diferença de potencial elétrico, em relação ao meio (cerca de -0,1V); mantida por um equilíbrio químico de concentração de íons dentro e fora da membrana plasmática.
Existem células que reagem estímulos elétricos apenas reestabelecendo o PR original por transporte passivo (sem gasto de energia) através da membrana, e estas são ditas células não-excitáveis.
Por outro lado, existem células que sob a ação do mesmo estímulo produzem um tipo de resposta bem característica: potencial de ação (PA); um pulso elétrico intenso (capaz de inverter a polarização do Potencial de Membrana) que se propaga ao longo da membrana da célula, sustentado por uma cadeia de transportes ativos (com gasto de energia) e que não decai ao longo do tempo e espaço; a esse tipo de células damos o nome de excitáveis[1].
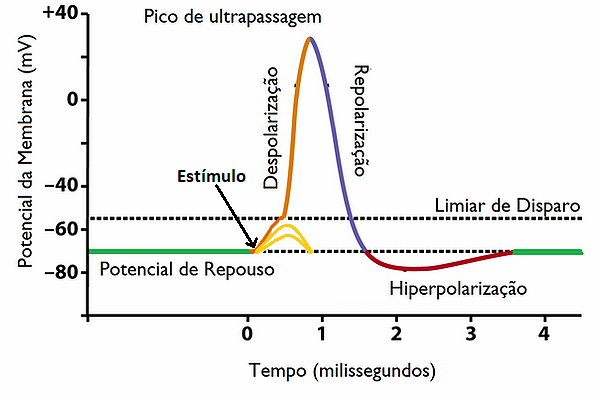
Os Neurônios são as células excitáveis do tecido nervoso (que constituem o encéfalo e medula espinhal, gânglios e nervos do reino animal) e com já vimos são capazes de gerar PA. Um potencial de ação pode assumir diversos formatos, mas ao longo do axônio (Figura 1) de um neurônio eles tendem a uma curva como a da Figura 2.
Olhando para Figura 2 vemos alguns aspectos importantes:
- O potencial de ação necessita de um estímulo mínimo (limiar) para ser ativado, abaixo desse valor o estímulo decai como em uma célula não excitável;
- Acima desse limiar a célula segue o principio de "Tudo ou Nada", ou seja, assume o valor máximo possivel dentro de sua capacidade, independente do estímulo aplicado;
- A etapa de despolarização (crescimento) é brusca e varia mais rapidamente que a repolarização (decaimento);
- O período que contém a repolarização e hiperpolarização da membrana é chamado período refratário, e se caracteriza por não permitir que ocorra nenhum disparo até que a membrana atinja o potencial de repouso.
Modelo
Premissa do modelo
Para iniciar a modelagem do sistema, devemos antes enfatizar três condições básicas que o potencial deve obedecer para que seja um PA [2]:
- Deve existir um limiar de voltagem para que um estímulo desencadeie o PA;
- Uma vez atingido o limiar, a voltagem deve aumentar até o máximo possível;
- Caso o estímulo não atinja o limiar, ele deve desaparecer rapidamente.
Podemos então definir como a variável normalizada que fará o papel da diferença de potencial elétrico no axônio, sendo que é definido como o potencial de repouso, é a diferença de potencial máxima suportada pela célula excitável e é o limiar de voltagem . Desta forma podemos escrever as condições acima como
Pode-se dizer que estas condições impõem que e sejam pontos de equilíbrio estável, enquanto seja um ponto de equilíbrio instável.
Assim, a variação temporal do potencial elétrico na célula pode ser dada por
Onde é alguma função que faz satisfazer as condições .
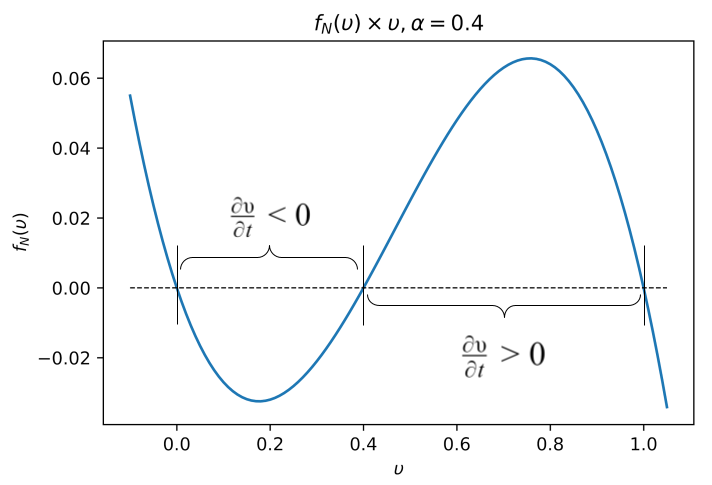
No modelo de Nagumo, utiliza-se o polinômio de terceiro grau .
Substituindo em é fácil notar que e são pontos de equilíbrio de . Por outro lado, como podemos ver na Figura 3, se , temos que logo o valor de diminui até atingir o ponto de equilíbrio em . Se fazendo o potencial crescer até atingir o valor máximo em . Desta forma, temos que e são pontos de equilíbrio estável —representando os pontos de potencial máximo e mínimo, respectivamente—, enquanto que é um ponto de equilíbrio instável, funcionando como o limiar de voltagem para desencadear o PA.
Em outras palavras, vemos o caráter "tudo ou nada" do potencial deste modelo. Se o valor do estímulo inicial se encontrar entre e , o estímulo desaparece, porém se o estímulo inicial estiver entre e , o estímulo é amplificado até o valor máximo. Entretanto, modelando o sistema apenas com a equação , vemos que o PA não é propagado por todo axônio, ele atua apenas localmente, onde ocorreu o estímulo. Além disso, uma vez estimulado, o neurônio nunca volta para o seu estado de repouso, permanecendo permanentemente no valor máximo de potencial.
Equação de Nagumo
A equação de Nagumo complementa o modelo acima adicionando um termo difusivo à equação . Assim temos que a equação de Nagumo é dada por[3][4]
Onde e .
Desta forma o PA não é mais restrito à região onde ocorre o estímulo e se difunde ao longo de todo axônio.
Modelo de Fitzhugh-Nagumo
O modelo de Fitzhugh-Nagumo (FN) complementa a equação de Nagumo introduzindo uma nova variável, transformando a equação original em um sistema de equações. A variável , chamada de "variável rápida", representa a variação do potencial na membrana da célula, enquanto que a nova variável , chamada de "variável lenta" ou variável de recuperação, representa a capacidade da célula retornar ao seu PR após ser excitada por um estímulo externo. o modelo de FN é dado pelo sistema de equações [3] [4] [5]
Onde é o limiar de potencial, é uma constante de difusão, e são parâmetros positivos a serem ajustados —relacionados à velocidade de atuação da variável de recuperação— e é a magnitude do estímulo externo [4] [5]
Método Crank-Nicolson
Uma equação diferencial parcial da forma
onde A, B e C são constantes, é chamada de equação quasilinear. Um método implícito no tempo e estável numericamente de solucionar este tipo de equação foi proposto na metade do século XX por John Crank e Phyllis Nicolson. O método de Crank-Nicolson é de segunda ordem no tempo e no espaço e é baseado em diferenças centradas no espaço e regra trapezoidal no tempo. Como provaremos mais adiante, este método é incondicionalmente estável.
A equação diferencial finita de Nagumo é dada pela segunda derivada espacial obtida a partir de uma combinação da derivada temporal no passo e :
A partir da equação (3.2), podemos obter os diferentes métodos de diferenciação da equação de Nagumo ajustando o valor de .
- é o método explícito.
- é o método implícito.
- é o método Crank-Nicolson.
Substituindo o valor de na equação (3.2), temos:
Para nosso problema, usaremos o método pseudo Crank-Nicolson, devido ao termo não-linear presente em (3.5).
Análise de Estabilidade de Von Neumann
Baseada nas deduções de G. Garcia [3].
Ao analisar a estabilidade do método, precisamos verificar se o erro gerado no procedimento não aumenta quando testamos os extremos da solução. Para realizar esta verificação, vamos utilizar o método de Von Neumann. A primeira coisa a se fazer é linearizar o termo não linear da equação (3.5):
Se substituírmos no tempo , onde e o método se mostra estável pelo seguinte:
Substituindo na equação (3.6), temos:
Substituindo em (3.7), temos:
Podemos notar que há em todos os termos. Simplificando-os e movendo todos os termos com para o lado esquerdo e todos com para a direita, a equação (3.8) toma a forma:
Fatorando os termos, ficamos com:
Utilizando a identidade trigonométrica , ficamos com:
Aplicando , temos:
Pode-se demonstrar que, a partir da equação (3.12), tem-se:
Como:
prova-se que o método Crank-Nicolson é estável para suficientemente pequenos.
Implementação para a equação de FitzHung-Nagumo
Para a implementação na equação de FitzHung-Nagumo, as seguintes derivadas parciais são utilizadas:
Neste ponto, utilizamos uma aproximação para a derivada temporal e a derivada espacial de segunda ordem e substituímos as equações (3.14), (3.15) e (3.16) na equação (2).
Multiplicando por , temos:
Fazendo a substituição:
e rearranjando, temos:
Podemos, então representar a equação (3.19) em forma matricial:
Onde o lado esquerdo da equação é a matriz tridimensional a seguir
e o lado direito:
Com isso, podemos encontrar as soluções da equação resolvendo:
FTCS Explícito
No método explícito, a discretização é
Substituindo na EDU e utilizando a notação de índices ( é índice temporal e é o índice temporal), temos
Agrupando em uma constante e deixando o passo temporal futuro em função do passo anterior explicitamente, temos
Utilizando esta equação é possível calcular o valor de iterativamente para todo intervalo de tempo.
FTCS Implícito
No método implícito, também chamado de BTCS (para trás no tempo centrado no espaço, do inglês: Backwards Time Centered Space), pois o passo temporal é dado para trás, assim a derivada temporal é
Resultando na seguinte EDU
Reescrevendo os índices temos
Onde está escrita implicitamente, e pode ser calculada utilizando o Algoritmo de Thomas [1].
Equação de Recuperação 1D
No modelo de Fitzhugh-Nagumo, utilizou-se o mesmo algoritmo de Crank-Nicolson utilizado na Equação de Nagumo, na seção 3.1. Entretanto, ainda é necessário resolver a equação diferencial de , dada por
Para isso utilizou-se o método FTCS explícito. Discretizando a derivada, temos
Utilizando a notação de índices e aplicando na equação da recuperação, temos
Assim, uma vez conhecido , é possível calcular para qualquer intervalo de tempo.
Vamos verificar as condições de estabilidade do método utilizando o os modos de Fourier:
- substituindo onde é a unidade imaginária;
- desconsiderando ,
temos
Dividindo ambos os lados por temos
Para que o método seja estável, temos que logo
Assim, temos que a condição de estabilidade sobre o método é tal que
Modelo FitzHung-Nagumo 2D
O sistema de EDP's em 2 dimensões, assumindo uma difusão isotrópica, é dado por
Lembrando que nesse formato assumimos pois os estímulos não serão constantes no tempo, serão dados na condição inicial.
Como a equação de recuperação já foi discretizada, e não depende da dimensão do problema, precisamos apenas aplicar o FTCS na equação de Nagumo em 2D. Assumindo , temos
onde os índices e se referem às coordenadas e , respectivamente, e o índice refere-se ao tempo.
Vamos verificar as condições de estabilidade do método utilizando os modos de Fourier:
- substituindo
- usando
- por simplicidade, como fizemos na seção 3.1, vamos linearizar
- por fim, desconsiderando , temos
Dividindo os dois lados da equação por temos
Sabendo as seguintes identidades trigonométricas:
e aplicando à equação, obtemos
Sabemos que a condição de estabilidade por modos de Fourier é obtida quando , portanto
.
Como e , no pior dos casos os termos de senos ao quadrado são 1, e a condição de estabilidade fica
.
Resultados
Equação de Nagumo 1D
Para as simulações numéricas foram utilizados os seguintes parâmetros:
Com isso, dividimos as simulações em dois casos.
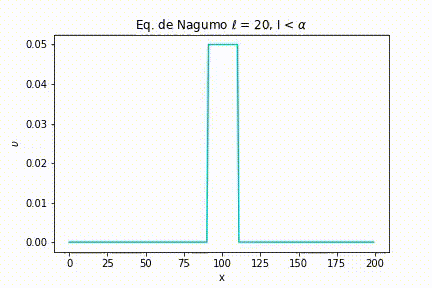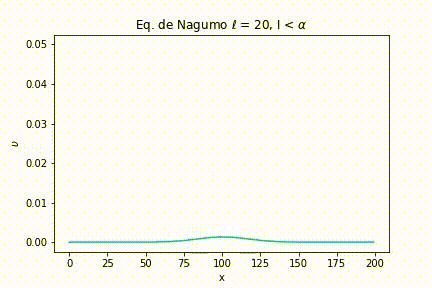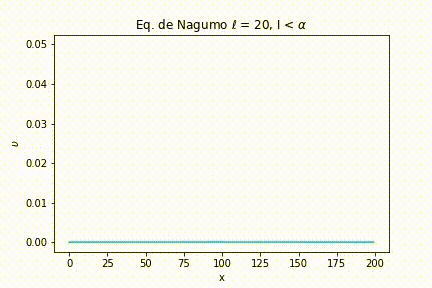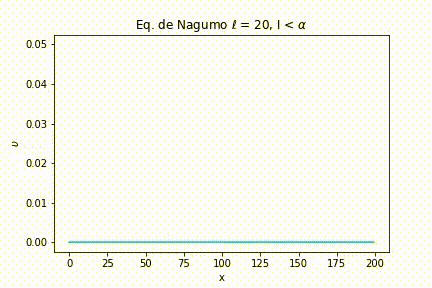
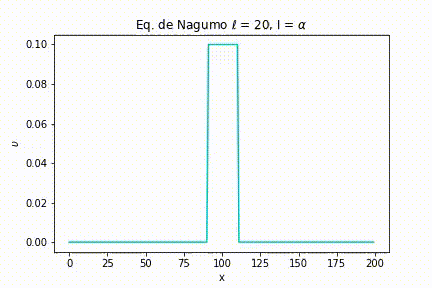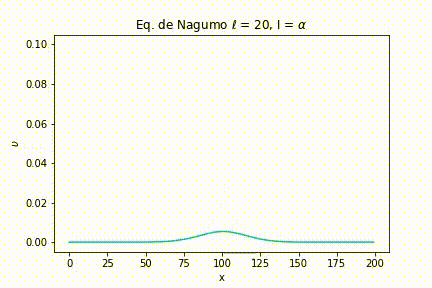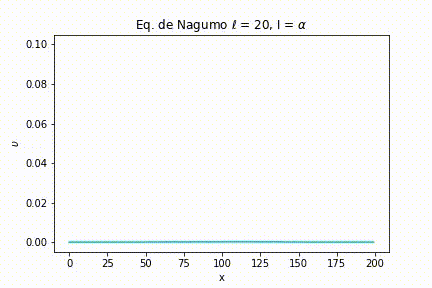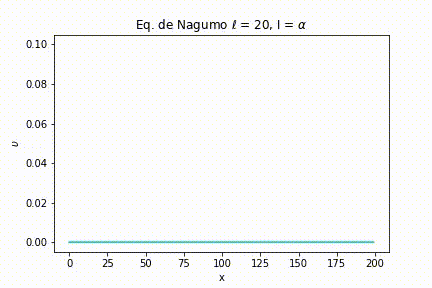
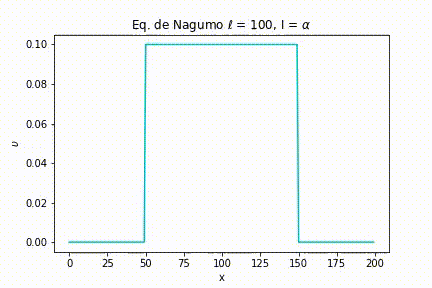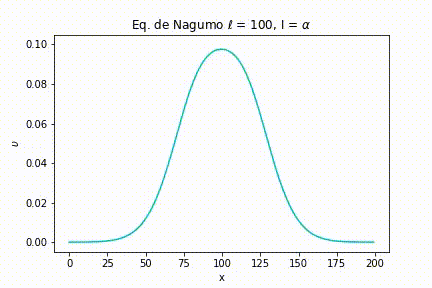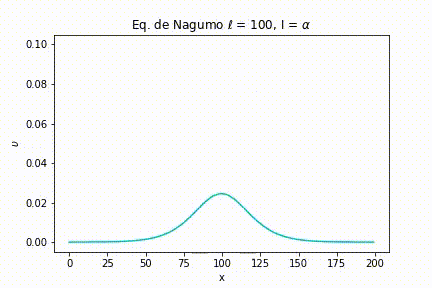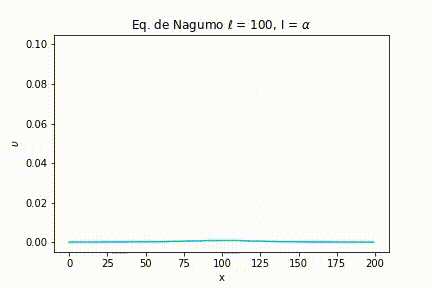
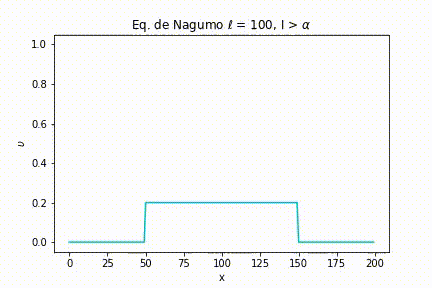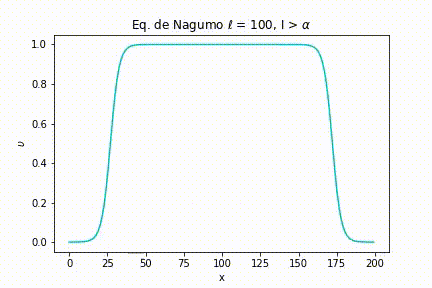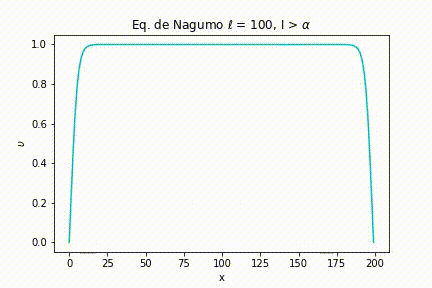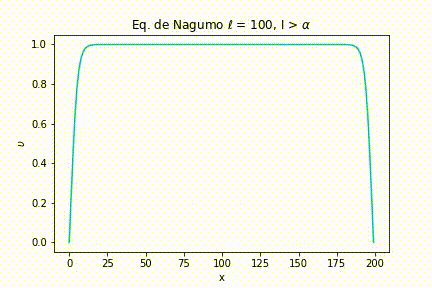
Caso I: As simulações foram geradas a partir da definição de uma largura de estímulo estreita . Com isso, variamos a intensidade do estímulo. Nas seguintes figuras, podemos ver as simulações para uma intensidade menor do que o limiar, igual ao limiar e maior que o limiar, respectivamente, , e .
Como pode ser visto na Figura 4, quando , ou seja, menor que o limiar, o sinal rapidamente se esvai.
Para uma intensidade igual ao limiar, o sinal também se extingue, porém com um intervalo de tempo maior do que anteriormente.
E, finalmente, quando a intensidade é maior que o limiar, não importa quão maior seja, o sinal é passado ao máximo da função.
Caso II: As seguintes simulações foram geradas a partir da definição de uma largura de estímulo larga .
Com isso, novamente a intensidade do estímulo é variada.
Para uma intensidade menor que o limiar, novamente o sinal se esvai.
O mesmo acontece quando a intensidade é igual ao limiar. Podemos notar que quando a largura é maior, o sinal se esvai mais lentamente se comparado a uma largura de sinal mais estreita.
Já quando a intensidade é maior que o limiar, o comportamento “tudo ou nada” novamente se mostra presente.
Modelo FitzHung-Nagumo 1D
Para a implementação da simulação do modelo FN em 1D utilizou-se (com ), (com ) e os demais parâmetros foram idênticos àqueles encontrados na ref.[1] [4]. Eles são
Foram aplicadas condições de contorno nulas nas bordas do intervalo de .
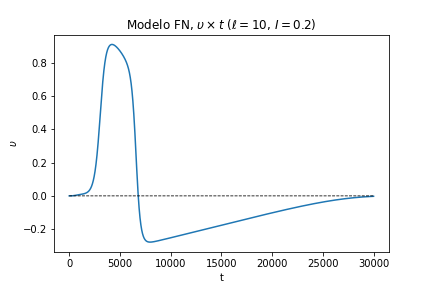
Na figura 10 vemos a evolução temporal do potencial elétrico em um ponto da membrana do axônio () quando excitado acima do limiar de potencial. Note que a curva do PA é muito semelhante àquela da na Figura 2, apresentando vários dos aspectos característicos, como a assimetria entre os períodos de polarização (ascensão rápida) e repolarização (decaimento mais lento) e um período refratário, onde o potencial lentamente se recupera em direção do PR. Podemos assim entender a escolha dos valores dos parâmetros e , que controlam a velocidade de crescimento da variável de recuperação (assim como se pode ver na equação (3)). Experimentalmente, sabemos que o período refratário é muito mais longo do que o período de despolarização [1] , logo precisamos que a intensidade da variável aumente muito lentamente. Para isso, escolhe-se valores pequenos de e , pois caso contrário o potencial da membrana celular não teria tempo de atingir o pico do PA.
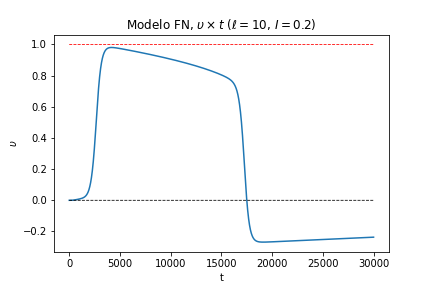
A velocidade de crescimento da variável de recuperação também explica a ausência do "tudo ou nada" no PA da figura 10. Na figura 11, vê-se a evolução temporal de um PA com (5 vezes menor do que aquele da figura 10).
Na figura 11, como a variável de recuperação cresce muito mais lentamente, além de demorar mais tempo para a membrana celular sair do período refratário, vemos que o pico do PA de ação é muito mais próximo do valor máximo. Isso ocorre porque a variável de recuperação cresce mais lentamente, possibilitando que a variável rápida atinja um valor maior antes de começar a diminuir devido à ação de .
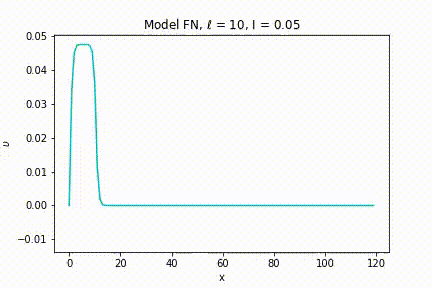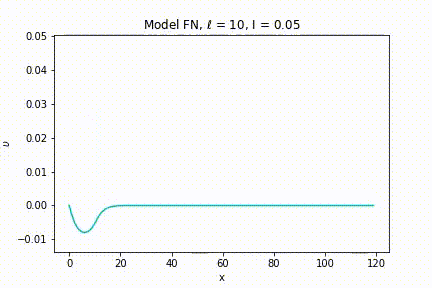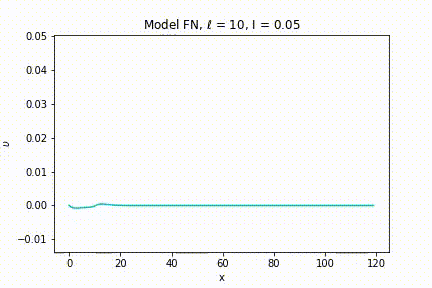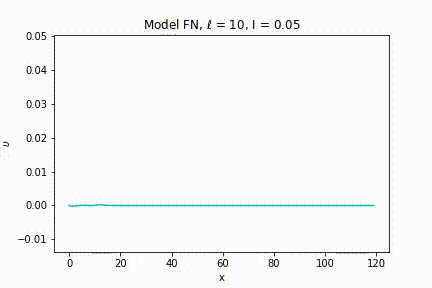
Nas animações das figuras 12 e 13 vemos a evolução espacial do potencial elétrico com o decorrer do tempo. Na figura 12, o estímulo inicial está abaixo do limiar de voltagem, desta forma ele não gera um PA e a célula volta rapidamente para o seu PR. Na figura 13 o estímulo inicial está acima do limiar, logo um PA é gerado e o pulso elétrico é propagado ao longo do axônio.
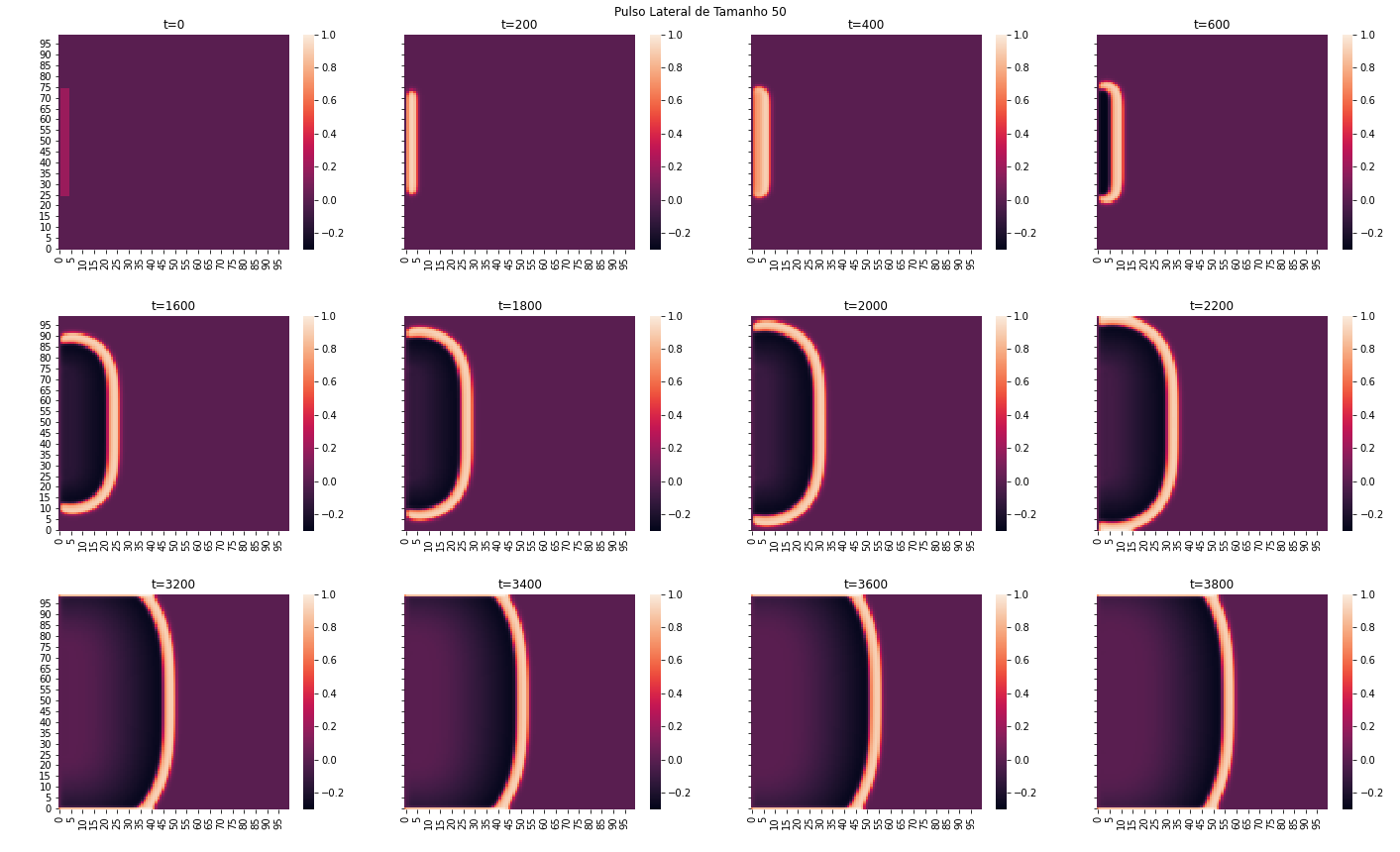
Modelo FitzHung-Nagumo 2D
As simulação 2D tinham por objetivo simular a propagação de um estimulo inicial de de espessura. Para se aproximar da simetria do problema(axônio como um cilindro por onde o PA se propaga) aplicamos condições periódicas na vertical, e mantivemos as bordas nulas na horizontal.
Os parâmetros adotados para e foram os mesmos da secção 5.2. O foi tomado como para uma maior velocidade de processamento.
Como podemos ver o PA se propaga assumindo um front de alta voltagem(despolarização e repolarização) estreito, e logo após uma região mais esparsa(de roxo mais escuro) indicando a repolarização da membrana da célula.
Discussão
Os resultados obtidos pela implementação da equação difusiva de Nagumo são análogos ao comportamento "tudo ou nada" de resposta em uma célula excitável, já que um estimulo acima do limiar levar ao aumento do potencial até um valor fixo. Embora esse valor não atinja o pico de ultrapassagem para todo estimulo inicial que esteja entre o limiar e a despolarização máxima da célula, essa peculiaridade é prevista pelo modelo [5]
Mas outra questão importante de se observar é a forma como diferentes larguras de estimulo inicial interferem na difusão do potencial elétrico na membrana. Um fenômeno que é verificável é que pulsos maiores difundem mais rápido sobre o axônio, já que os efeitos de inversão de campo elétrico na região do estímulo podem ser percebidos nas proximidades mesmo antes do estímulo chegar ali [1].
Quanto a implementação do Sistema FitzHung-Nagumo com potencial difusivo sobre a membrana, vemos que o potencial(nos gráficos de v por t) de ação é gerado com um perfil bem semelhante a um PA convencional de axônio. Para manter o sentido fisiológico escolhemos fazer as simulações para um [1],que como mencionado na seção 2.3 não consegue reagir a estímulos contínuos, nem após o período refratário, ainda é muito confiável para simular estímulos únicos.
A maioria dos estudos no modelo FitzHung-Nagumo utiliza as soluções oscilatórias decorrentes , mas embora essa abordagem leve a uma gama maior de resultados para estímulo contínuo [5] [4] o sentido fisiológico é prejudicado, principalmente pelo fato de não possuir um limiar [5].
Programas
Cranck Nicolson e FTCS Modelo FitzHung-Nagumo 1D
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from matplotlib.animation import ArtistAnimation
#Definindo Polinômio de Nagumo
def Pol(u):
a = 0.1
return u*(1 - u)*(u - a)
#Declarando Constantes
L = 100
D = 0.1
dt = 1
dx = 1
r = (D*dt)/(dx**2)
#Definindo função que calcula a equação de recuperação 1D
def FitzHung_FTCS(v, w):
D = 0.1
dx = 1
r = (D*dt)/(dx**2)
L = len(v)
aux = w[:]
for i in range(1, L-1):
aux[i] = w[i] + (r/(D*2))*0.005*(v[i] - 0.0001*w[i])
for j in range(1, L-1):
w[j] = aux[j]
return (w)
#Criando matriz tridiagonal para o método de Thomas
for i in range(L):
for j in range(L):
if i == j:
A[i,j] = 1 - 2*r
if j == i+1:
A[i,j] = r
if j == i-1:
A[i,j] = r
#Definindo função que calcula Equação de Nagumo 1D por método de Thomas
def Nagumo_CN(d,w,A):
L = len(d)
d = np.array(d)
D = 0.1
dt = 1
dx = 1
r = (D*dt)/(dx**2)
aux = np.dot(A, d)
aux[0] = d[0]
aux[L-1] = d[L-1]
for i in range(L):
d[i] = aux[i] + (r*Pol(aux[i]))/(D*2) - (r*w[i])/(2*D) + (r/(2*D))*I[i]
a = (-1*r)*(np.ones(L, dtype = np.float32))
b = (2*r + 1)*(np.ones(L, dtype = np.float32))
c = (-1*r)*(np.ones(L, dtype = np.float32))
c[L-1] = 0
g = [x for x in d]
c[0] = c[0]/b[0]
for i in range(1,L-1) :
c[i] = c[i]/(b[i] - (c[i-1]*a[i]))
for i in range(1,L-1) :
d[i] = (d[i] - (d[i-1]*a[i]))/(b[i] - (c[i-1]*a[i]))
g[L-1] = d[L-1]
for i in range(L-2,0,-1) :
g[i] = (d[i] - c[i]*g[i+1])
return (g)
#calculando o modelo FN
f = np.zeros(L, dtype = np.float32)
w = np.zeros(L, dtype = np.float32)
f[1:11] = 0.2
h = np.zeros(30000, dtype = np.float32)
T = np.arange(30000, dtype = np.float32)
x = np.arange(L, dtype = np.float32)
t = 0
h[0] = f[15]
for m in range(1, 30000):
aux = f[:]
f = Nagumo_CN(f, w, A)
w = FitzHung_FTCS(aux , w)
h[m] = f[15]
t = m*dt
#plot das figuras 10 e 11
ones = np.ones(30000)
zeros = np.zeros(30000)
plt.title('Modelo FN, $\\upsilon \\times t$ ($\ell = 10$, $I = 0.2$)')
plt.xlabel('t')
plt.ylabel('$\\upsilon$')
plt.plot(T, h)
plt.plot(T, ones,'r--', linewidth=0.8)
plt.plot(T, zeros, 'k--', linewidth = 0.8)
plt.savefig('nomedoarquivo.png')
#plot das animações
f = np.zeros(L, dtype = np.float32)
w = np.zeros(L, dtype = np.float32)
f[1:11] = 0.2
x = np.arange(L, dtype = np.float32)
t = 0
n = 1
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
frames = []
plt.title('Model FN, $\\ell$ = 10, I = 0.2')
plt.ylabel('$\\upsilon$')
plt.xlabel('x')
for m in range(1, 10000):
if (t == n):
curve = ax.plot(x, f, 'c')
frames.append(curve)
n = n + 1
aux = f[:]
f = Nagumo_CN(f, w, A)
w = FitzHung_FTCS(aux , w)
t = m*dt
animacao = ArtistAnimation(fig, frames, interval=50, blit=True)
animacao.save('nomedoarquivo.mp4')
FTCS Modelo FitzHung-Nagumo 2D
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
import seaborn as sb
#Definindo Polinômio de Nagumo
def Pol(u):
a = 0.1
return u*(1 - u)*(u - a)
#Declarando Constantes
L = 100
D = 0.1
dt = 1
dx = 1
r = (D*dt)/(dx**2)
#Definindo função que calcula a equação de recuperação 2D
def FitzHung2D_FTCS(v, w):
D = 0.1
dt = 1
dx = 1
r = (D*dt)/(dx**2)
L = len(v)
aux = w[:]
for i in range(1, L-1):
for j in range(1, L-1):
aux[i,j] = w[i,j] + dt*0.005*(v[i,j] - 0.0001*w[i,j])
for i in range(1, L-1):
for j in range(1, L-1):
w[i,j] = aux[i,j]
return (w)
#Definindo função que calcula a equação de Nagumo em 2D como condições periódicas em y
def Nagumo2D_FTCS(v, w):
D = 0.1
dt = 1
dx = 1
r = (D*dt)/(dx**2)
L = len(v)
aux = v[:,:]
for j in range(1,L-1):
aux[0,j] = v[0,j] + r*(v[ L-1 ,j] + v[1,j] + v[0,j-1] + v[0,j+1] -4*v[0,j]) + dt*Pol(v[0,j]) - dt*w[0,j]
aux[0,L-1] = v[0,L-1] + r*(v[ L-1 ,L-1] + v[1,L-1] + v[0,L-2] + 0 -4*v[0,L-1]) + dt*Pol(v[0,L-1]) - dt*w[0,L-1]
for i in range(1, L-1):
for j in range(1, L-1):
aux[i,j] = v[i,j] + r*(v[i-1,j] + v[i+1,j] + v[i,j-1] + v[i,j+1] -4*v[i,j]) + dt*Pol(v[i,j]) - dt*w[i,j]
for j in range(1,L-1):
aux[L-1,j] = v[L-1,j] + r*(v[L-2,j] + v[0,j] + v[L-1,j-1] + v[L-1,j+1] -4*v[L-1,j]) + dt*Pol(v[L-1,j]) - dt*w[L-1,j]
aux[L-1,L-1] = v[L-1,L-1] + r*(v[L-2,L-1] + v[0,L-1] + v[L-1,L-2] + 0 -4*v[L-1,L-1]) + dt*Pol(v[L-1,L-1]) - dt*w[L-1,L-1]
for i in range(1, L):
for j in range(1, L-1):
v[i,j] = aux[i,j]
return (v)
#Função criada para evitar o uso de estruturas booleanas dentro do loop, que torna a simulação mais demorada
def Para_Evitar_Ifs(g):
intervalo = 20
T = g[0]
v = g[1]
w = g[2]
for t in range(T,T + intervalo):
aux = v[:,:]
v = Nagumo2D_FTCS(v, w)
w = FitzHung2D_FTCS(aux , w)
return ([T+intervalo,v,w])
#Criando os espaço e o grid de fotos
x = np.arange(L, dtype = np.float32)
y = np.arange(L, dtype = np.float32)
T = 0
dl = 4
p1 = (dl/2) - 1
p2 = (dl/2) + 1
tamanho = 2*L/dl
x,y = np.meshgrid(x,y)
f, (ax1,ax2,ax3,ax4) = plt.subplots(1,4,sharey=True, figsize=(24,4))
f.suptitle('Pulso Lateral de Tamanho '+str(int(tamanho))+'')
#Declarando condições iniciais e condições de contorno não periódicas
v = np.zeros((L,L))
v[int(p1*tamanho/2)-6:int(p2*tamanho/2),1:5] = 0.2
w = np.zeros((L,L))
#Plotando os 4 primeiros mapas de calor
g = [T,v,w]
graph1 = sb.heatmap(g[1],cbar=True,vmin = -0.3, vmax = 1,ax=ax1)
graph1.set_title('t='+str(g[0])+'')
graph1.invert_yaxis()
g = Para_Evitar_Ifs(g)
graph2 = sb.heatmap(g[1],cbar=True,vmin = -0.3, vmax = 1,ax=ax2)
graph2.set_title('t='+str(g[0])+'')
graph2.invert_yaxis()
g = Para_Evitar_Ifs(g)
graph3 = sb.heatmap(g[1],cbar=True,vmin = -0.3, vmax = 1,ax=ax3)
graph3.set_title('t='+str(g[0])+'')
graph3.invert_yaxis()
g = Para_Evitar_Ifs(g)
graph4 = sb.heatmap(g[1],cbar=True,vmin = -0.3, vmax = 1,ax=ax4)
graph4.set_title('t='+str(g[0])+'')
graph4.invert_yaxis()
plt.savefig('Lateral_1.png')
plt.show()
Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 https://www.ufrgs.br/mnemoforos/arquivos/potenciais2005.pdf Jorge A. Quillfeldt,"ORIGEM DOS POTENCIAIS ELÉTRICOS DAS CÉLULAS NERVOSAS"
- ↑ https://youtu.be/H9yxE9yrH5w%7C A simple spiking neuron model: sodium channels alone
- ↑ 3,0 3,1 3,2 https://tamiu-ir.tdl.org/bitstream/handle/2152.4/60/GARCIA-THESIS-2015.pdf?sequence=1&isAllowed=y Gabriel Perry Natanni Garcia, "NUMERICAL SIMULATION OF THE NAGUMO EQUATION BY FINITE DIFFERENCEMETHOD"
- ↑ 4,0 4,1 4,2 4,3 4,4 https://hal.inria.fr/hal-00998828/document Binbin Xu, Stéphane Binczak, Sabir Jacquir, Oriol Pont, Hussein Yahia. Parameters Analysis of
FitzHugh-Nagumo Model for a Reliable Simulation. 36th Annual International Conference of the
IEEE Engineering in Medicine and Biology Society (EMBC’14), IEEE Engineering in Medicine and
Biology Society, Aug 2014, Chicago, United States. ffhal-00998828 Erro de citação: Etiqueta inválida
<ref>; Nome "PARAMETERS" definido várias vezes com conteúdo diferente - ↑ 5,0 5,1 5,2 5,3 5,4 http://www.scholarpedia.org/article/FitzHugh-Nagumo_model Eugene M. Izhikevich and Richard FitzHugh (2006), Scholarpedia, 1(9):1349., "FITZHUGH-NAGUMO MODEL"













































































































![{\displaystyle {\frac {v_{l,j}^{n+1}-v_{l,j}^{n}}{\Delta t}}={\frac {D}{(\Delta x)^{2}}}\left[(v_{l-1,j}^{n}-2v_{l,j}^{n}+v_{l+1,j}^{n})+(v_{l,j-1}^{n}-2v_{l,j}^{n}+v_{l,j+1}^{n})\right]+f_{Nl,j}^{n}-w_{l,j}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0154fe744bd0239162db63ca72deb69d734c2ec4)
![{\displaystyle v_{l,j}^{n+1}=v_{l,j}^{n}+{\frac {D\Delta t}{(\Delta x)^{2}}}\left[(v_{l-1,j}^{n}-2v_{l,j}^{n}+v_{l+1,j}^{n})+(v_{l,j-1}^{n}-2v_{l,j}^{n}+v_{l,j+1}^{n})\right]+\Delta tf_{Nl,j}^{n}-\Delta tw_{l,j}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e89e1856a9a6e36fec7eeb0b33e198e36c2c4408)
![{\displaystyle v_{l,j}^{n+1}=v_{l,j}^{n}+{\frac {D\Delta t}{(\Delta x)^{2}}}\left[v_{l-1,j}^{n}+v_{l+1,j}^{n}+v_{l,j-1}^{n}+v_{l,j+1}^{n}-4v_{l,j}^{n}\right]+\Delta tf_{Nl,j}^{n}-\Delta tw_{l,j}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18472d58e1b91f412aadfba21b806d85bcdf4070)







![{\displaystyle A^{n+1}e^{i\beta }=A^{n}e^{i\beta }+rA^{n}\left[e^{i((x-\Delta x)q_{x}+yq_{y})}+e^{i((x+\Delta x)q_{x}+yq_{y})}+e^{i(xq_{x}+(y-\Delta y)q_{y})}+e^{i(xq_{x}+(y+\Delta y)q_{y})}-4e^{i\beta }\right]-\Delta t\alpha A^{n}e^{i\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45d4d9ba03f6178631a93c65e0d5503a819b13b)
![{\displaystyle A^{n+1}e^{i\beta }=A^{n}e^{i\beta }+rA^{n}e^{i\beta }\left[e^{-i\Delta xq_{x}}+e^{i\Delta xq_{x}}+e^{-i\Delta yq_{y}}+e^{i\Delta yq_{y}}-4\right]-\Delta t\alpha A^{n}e^{i\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec31c3c64c807fa1a854fca0e700c03a35710920)

![{\displaystyle {\frac {A^{n+1}}{A^{n}}}=1+r\left[e^{-i\Delta xq_{x}}+e^{i\Delta xq_{x}}+e^{-i\Delta yq_{y}}+e^{i\Delta yq_{y}}-4\right]-\Delta t\alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/82fb835e20cc55eb01f15f6737448a123571c89b)


![{\displaystyle {\frac {A^{n+1}}{A^{n}}}=1+2r\left[\cos(\Delta xq_{x})+\cos(\Delta yq_{y})-2\right]-\Delta t\alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e34ca22db3e0e394e488b1919cf19535c08beb87)
![{\displaystyle {\frac {A^{n+1}}{A^{n}}}=1+2r\left[(1-2\sin ^{2}(\Delta xq_{x}/2))+(1-2\sin ^{2}(\Delta yq_{y}/2))-2\right]-\Delta t\alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/28a4f020eb999eac841b1a75c613278ca0b5e199)
![{\displaystyle {\frac {A^{n+1}}{A^{n}}}=1+4r\left[\sin ^{2}(\Delta xq_{x}/2)+\sin ^{2}(\Delta yq_{y}/2)\right]-\Delta t\alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de23ed920067151d5863fe7034eac8e341e2979)

![{\displaystyle \left|1-\Delta t\alpha +4r\left[\sin ^{2}(\Delta xq_{x}/2)+\sin ^{2}(\Delta yq_{y}/2)\right]\right|<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdebb663c886b4f9b81112d8c2474065bc61e46)