Mudanças entre as edições de "Modelo de Fitzhugh-Nagumo para o potencial de ação de neurônios"

Edição das 23h39min de 1 de abril de 2021

Grupo: Bernardo Boatini, Murilo Kessler Azambuja e Natália Ferrazzo

O objetivo deste trabalho é implementar e estudar a dinâmica do modelo FitzHungh-Nagumo, e das equações que o compõem, para potenciais de ação em células e tecidos excitáveis. O método computacional utilizado para resolver os problemas e implementar o modelo foi o FTCS (Forward Time Centered Space) e o método de Crank-Nicolson.

Potencial de Ação em Neurônios

A células vivas são sistemas eletricamente sensíveis, ou seja, podem reagir a estímulos elétricos. Isso se dá devido ao fato de que substâncias carregadas estão naturalmente vinculadas a seus processos internos de interação com o ambiente, principalmente por intermédio de canais iônicos e proteínas transmebrana como, por exemplo, a Bomba de Sódio e Potássio(Bomba Na⁺/K⁺ ATPase)^[1].

Naturalmente todas as células vivas possuem um potencial de repouso(PR) elétrico, ou seja, uma diferença de potencial elétrico, em relação ao meio(cerca de 0,1); mantida por um equilíbrio químico de concentração de íons dentro e fora da membrana plasmática.

Existem células que reagem estímulos elétricos apenas reestabelecendo o PR original por transporte passivo(sem gasto de energia) através da membrana, e estas são ditas células não-excitáveis.

Por outro lado, existem células que sob a ação do mesmo estímulo produzem um tipo de resposta bem característica: potencial de ação(PA); um pulso elétrico intenso(capaz de inverter a polarização do Potencial de Membrana) que se propaga ao longo da membrana da célula, sustentado por uma cadeia de transportes ativos(com gasto de energia) e que não decai ao longo do tempo e espaço; a esse tipo de células damos o nome de excitáveis^[1].

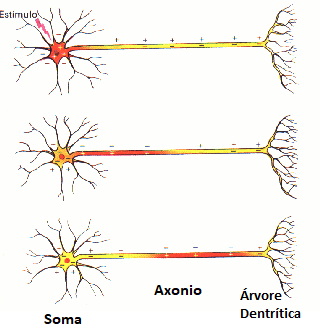
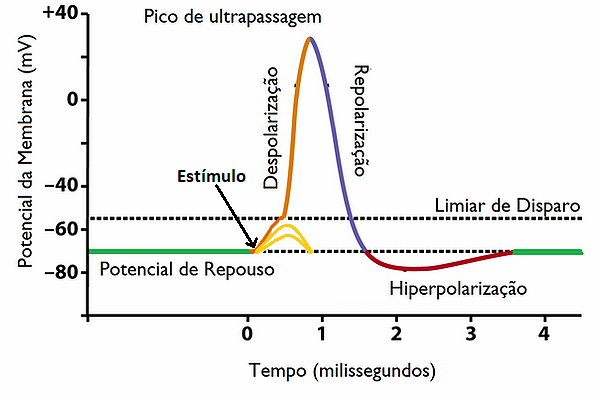
Os Neurônios são as células excitáveis do tecido nervoso(que constituem o encéfalo e medula espinhal, gânglios e nervos do reino animal) e com já vimos são capazes de gerar PA. Um potencial de ação pode assumir diversos formatos, mas ao longo do axônio(Figura 1) de um neurônio eles tendem a uma curva como a da Figura 2.

Figura 1 -Representação de um potencial de ação(vermelho) ao longo de um axônio de neurônio, partindo do soma neural em direção a arvore dentrítica.

Figura 2 -Curva de um Potencial de Ação genérico no tempo, em um ponto do axônio de um neurônio.

Olhando para Figura 2 vemos alguns aspectos importantes:

• O potencial de ação necessita de um estímulo mínimo(limiar) para ser ativado, abaixo desse valor o estímulo decai como em uma célula não excitável;
• Acima desse limiar a célula segue o principio de "Tudo ou Nada", ou seja, assume o valor máximo possivel dentro de sua capacidade, independente do estímulo aplicado;
• A etapa de despolarização(crescimento) é brusca e varia mais rapidamente que a repolarização(decaimento);
• O período que contém a repolarização e hiperpolarização da membrana é chamado período refratário, e se caracteriza por não permitir que ocorra nenhum disparo até que a membrana atinja o potencial de repouso.

Modelo

Premissa do modelo

Para iniciar a modelagem do sistema, devemos antes enfatizar três condições básicas que o potencial deve obedecer para que seja um PA ^[2]:

• Deve existir um limiar de voltagem para que um estímulo desencadeie o PA;
• Uma vez atingido o limiar, a voltagem deve aumentar até o máximo possível;
• Caso o estímulo não atinja o limiar, ele deve desaparecer rapidamente.

Podemos então definir como a variável normalizada que fará o papel da diferença de potencial elétrico no axônio, sendo que é definido como o potencial de repouso, é a diferença de potencial máxima suportada pela célula excitável e é o limiar de voltagem . Desta forma podemos escrever as condições acima como

Pode-se dizer que estas condições impõem que e sejam pontos de equilíbrio estável, enquanto seja um ponto de equilíbrio instável.

Assim, a variação temporal do potencial elétrico na célula pode ser dada por

Onde é alguma função que faz satisfazer as condições .

No modelo de Nagumo, utiliza-se o polinômio de terceiro grau .

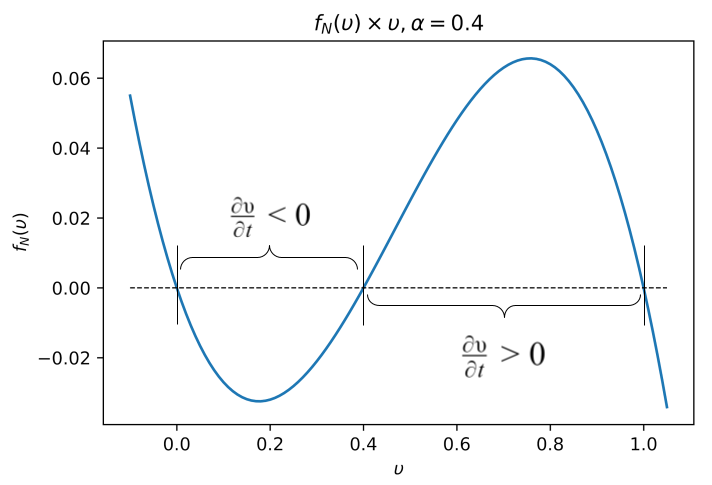
Substituindo em é fácil notar que e são pontos de equilíbrio de . Por outro lado, como podemos ver na Figura 3, se , temos que logo o valor de diminui até atingir o ponto de equilíbrio em . Se fazendo o potencial crescer até atingir o valor máximo em . Desta forma, temos que e são pontos de equilíbrio estável —representando os pontos de potencial máximo e mínimo, respectivamente—, enquanto que é um ponto de equilíbrio instável, funcionando como o limiar de voltagem para desencadear o PA.

Figura 3 — Curva de com

Em outras palavras, vemos o caráter "tudo ou nada" do potencial deste modelo. Se o valor do estímulo inicial se encontrar entre e , o estímulo desaparece, porém se o estímulo inicial estiver entre e , o estímulo é amplificado até o valor máximo. Entretanto, modelando o sistema apenas com a equação , vemos que o PA não é propagado por todo axônio, ele atua apenas localmente, onde ocorreu o estímulo. Além disso, uma vez estimulado, o neurônio nunca volta para o seu estado de repouso, permanecendo permanentemente no valor máximo de potencial.

Equação de Nagumo

A equação de Nagumo complementa o modelo acima adicionando um termo difusivo à equação . Assim temos que a equação de Nagumo é dada por^[3][4]

Onde e .

Desta forma o PA não é mais restrito à região onde ocorre o estímulo e se difunde ao longo de todo axônio.

Modelo de Fitzhugh-Nagumo

O modelo de Fitzhugh-Nagumo (FN) complementa a equação de Nagumo introduzindo uma nova variável, transformando a equação original em um sistema de equações. A variável , chamada de "variável rápida", representa a variação do potencial na membrana da célula, enquanto que a nova variável , chamada de "variável lenta" ou variável de recuperação, representa a capacidade da célula retornar ao seu PR após ser excitada por um estímulo externo. o modelo de FN é dado pelo sistema de equações ^[3]

Método de Crank-Nicolson

(explicar o método --> Natália)

Equação de Nagumo 1D

(aplicar o método na equação e testar estabilidade --> Natália)

Método FTCS

(explicar o método --> Murilo)

Equação de Recuperação 1D

(aplicar o método na equação e testar estabilidade --> Murilo))

Modelo FitzHung-Nagumo 2D

(aplicar o método na equação e testar estabilidade --> Bernardo)

O sistema de EDP's em 2 dimensões, assumindo uma difusão isotrópica, é dado por

Como a equação de recuperação já foi discretizada, e não depende da dimensão do problema, precisamos apenas aplicar o FTCS na equação difusiva de naumo em 2D, assumindo , temos

na qual os índices e se referem às coordenadas e respectivamente; e o índice referente ao tempo.

Vamos verificar as condições de estabilidade do problema por modos de Fourier, ou seja, substituindo

Resultados

Equação de Nagumo 1D

(explicar os testes e os gráficos/animações --> Natália)

Modelo FitzHung-Nagumo 1D

(explicar os testes e os gráficos/animações --> Murilo)

Modelo FitzHung-Nagumo 2D

(explicar os testes e os gráficos/animações --> Bernardo)

Discussão

(Contextualizar resultados --> Bernardo)

Programas

Referências

1. ↑ ^{1,0 1,1} https://www.ufrgs.br/mnemoforos/arquivos/potenciais2005.pdf Jorge A. Quillfeldt,"ORIGEM DOS POTENCIAIS ELÉTRICOS DAS CÉLULAS NERVOSAS"
2. ↑ https://youtu.be/H9yxE9yrH5w
3. ↑ ^{3,0 3,1} https://tamiu-ir.tdl.org/bitstream/handle/2152.4/60/GARCIA-THESIS-2015.pdf?sequence=1&isAllowed=y Gabriel Perry Natanni Garcia, "NUMERICAL SIMULATION OF THE NAGUMO EQUATION BY FINITE DIFFERENCEMETHOD"
4. ↑ https://hal.inria.fr/hal-00998828/document

• 5. Eugene M. Izhikevich and Richard FitzHugh, "FitzHugh-Nagumo model"