Modelo de Bornholdt para simulação de mercados financeiros artificiais: mudanças entre as edições
| Linha 7: | Linha 7: | ||
Podemos fazer um paralelo interessante entre os spins e a sua interação com seus vizinhos com ''traders'' em mercados finaceiros e a suas interações com outros ''traders''. No caso do Modelo de Ising, podemos interpretar cada spin como um ''trader'', ou agente, em um mercado financeiro e a direção da componente Z desse spin como a sua estratégia de compra ou venda. Então neste caso mais simples, para <math>J_{ij} > 0</math>, os agentes tenderão a adotar a mesma estratégia de mercado, e isso não descreve bem a realidade dos mercados. | Podemos fazer um paralelo interessante entre os spins e a sua interação com seus vizinhos com ''traders'' em mercados finaceiros e a suas interações com outros ''traders''. No caso do Modelo de Ising, podemos interpretar cada spin como um ''trader'', ou agente, em um mercado financeiro e a direção da componente Z desse spin como a sua estratégia de compra ou venda. Então neste caso mais simples, para <math>J_{ij} > 0</math>, os agentes tenderão a adotar a mesma estratégia de mercado, e isso não descreve bem a realidade dos mercados. | ||
O Modelo de Bornholdt, se incluid {coisas do artigo}. Assim, o hamiltoniano do sistema fica complementado: | |||
<math>\mathcal{H} = \sum_{\langle i, j \rangle} J_{ij} S_i S_j - \sum_{i} \alpha C_i(t) \frac{1}{N} \sum_{j} S_j(t)</math> | |||
onde <math>\alpha</math> é o termo de acomplamento do spin com a rede toda <math>(\alpha > 0)</math> | |||
==Alguns conceitos importantes== | ==Alguns conceitos importantes== | ||
Edição das 15h50min de 22 de maio de 2021
Grupo: Leonardo Barcelos, Luana Bianchi e Rubens Borrasca
Modelo de Bornholdt
Para estudar os fenômenos físicos que nos rodeiam, usamos modelos matemáticos para entender como sistemas evoluem com o tempo. No entanto, esses modelos muitas vezes podem ser base para estudos além do sistema físico de interesse. Para um sistema de spins, um dos modelos mais simples, que leva em conta apenas a interação de cada spin com seus primeiros vizinhos, é o Modelo de Ising. O hamiltoniano que o descreve é defindo pela segunte expressão:
onde é o termo que define a força de interação entre os spins i e j e a componente Z do spin. Além disso denota que estamos somando somente sobre os primeiros vizinhos. Para um valor de , a interação ferromagnética é favorecida, e os spins vizinhos tendem a se alinhar conjuntamente, formando domínios magnéticos. No entanto, para a interação antiferromagnética é favorecida, e os spins tende a se "anti-alinhar".
Podemos fazer um paralelo interessante entre os spins e a sua interação com seus vizinhos com traders em mercados finaceiros e a suas interações com outros traders. No caso do Modelo de Ising, podemos interpretar cada spin como um trader, ou agente, em um mercado financeiro e a direção da componente Z desse spin como a sua estratégia de compra ou venda. Então neste caso mais simples, para , os agentes tenderão a adotar a mesma estratégia de mercado, e isso não descreve bem a realidade dos mercados.
O Modelo de Bornholdt, se incluid {coisas do artigo}. Assim, o hamiltoniano do sistema fica complementado:
onde é o termo de acomplamento do spin com a rede toda
Alguns conceitos importantes
Retornos
Quando se trata de sistemas financeiros, os estudos se concentram mais no retorno dos ativos do que no preço em si, pois a série temporal dos retornos tem propriedades estatísticas mais interessantes que a série dos preços.
Sendo P(t) o preço de um ativo financeiro no instante t, e P(t-1) o preço do ativo no instante (t-1), o retorno linear do ativo é:
Reescrevendo esta equação, obtemos que:
Aplicando a função logarítmica em ambos os lados da equação, e considerando que:
obtêm-se o retorno logarítmico, que é mais indicado quando se têm ativos voláteis, que possuem uma variação muito alta:
Considerando que neste estudo serão comparados retornos de diferentes índices, e também os retornos obtidos através das simulações com o modelo de Bornholdt, é importante normalizar os retornos:
em que é o desvio padrão da serie de retornos e a média.
Distribuição dos Retornos
Quando se tem um volume considerável de dados é possível obter a distribuição probabilística deles. Para isso pode-se utilizar a estimação de densidade de Kernel (KDE). Ao observar uma pequena janela de tamanho h em torno de um ponto em análise, pode-se dizer que:
sendo uma função kernel e uma variável tal que:
Para este estudo utilizou-se um kernel gaussiano:
Este método foi aplicado para as séries de retorno para obter a distribuição deles, utilizando .
Volatilidade
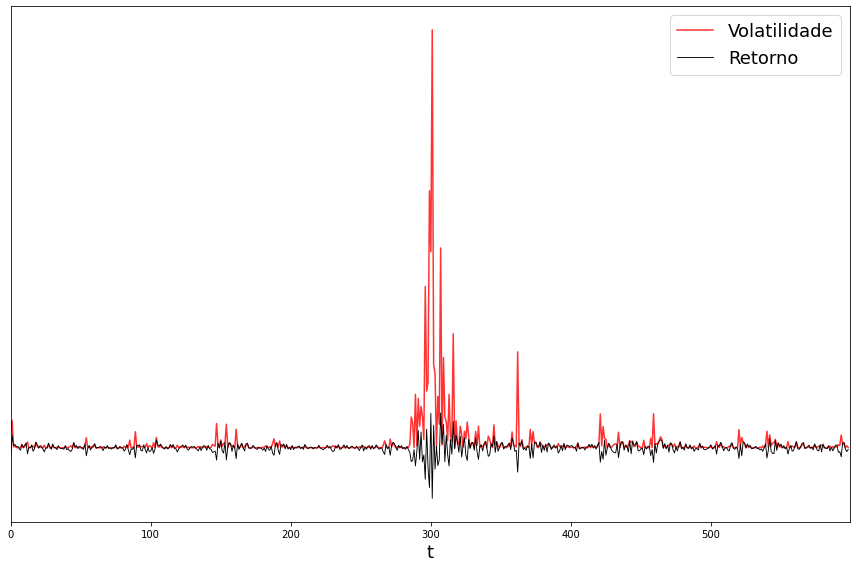
Uma forma de calcular a volatilidade da série temporal de retornos ao longo do tempo é elevar ao quadrado os valores da série. Deste modo pode-se obter uma variável como a que está ilustrada na figura abaixo:
O interessante em estudar volatilidade de retornos financeiros é que essa variável reflete o quão imprevisível é um determinado ativo. Uma ação com alta volatilidade tende a ter um risco maior de investimento, ao passo que ações com baixa volatilidade geralmente retornam riscos menores, pois seu comportamento acaba sendo mais previsível.
Um fato estilizado financeiro é que a volatilidade das séries temporais de retorno apresentam comportamento sazonal por natureza. Há períodos de alta volatilidade, seguidos por períodos com baixa volatilidade, que então são novamente seguidos por alta volatilidade, e assim adiante. E uma forma de mensurar isto é verificando a presença de clusters de autocorrelação na volatilidade de retornos. Isto é, através da análise da autocorrelação da volatilidade, encontrar bolhas que indiquem as fases destes comportamentos.
Para obter a auto correlação o Teorema de Wiener-Khinchin foi utilizado, de forma que:
onde é a transformada de Fourier do quadrado dos retornos.
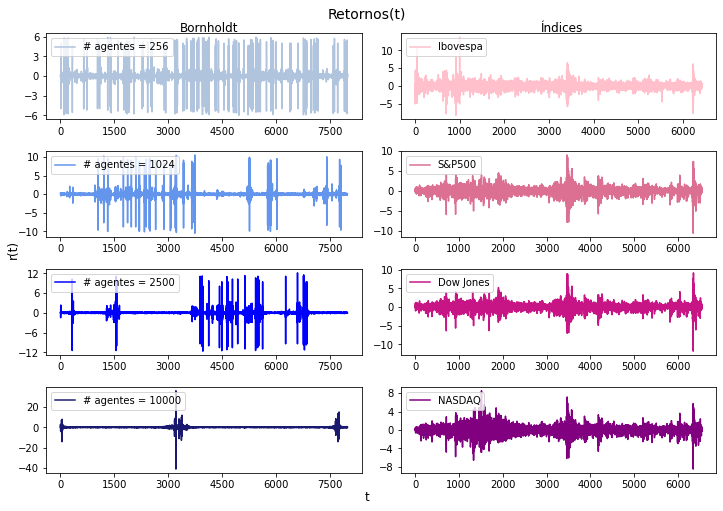
Simulações
Variação do tamanho da grade
Em Julia, 8000 passos de MC 16x16: 0.512 s 32x32: 2.332 s 50x50: 10.674 s 100x100: 154.134 s