Mudanças entre as edições de "Grupo2 - Ondas1"

De Física Computacional
Ir para: navegação, pesquisa
(→‎Programas)
(→‎Programas)
Linha 259: Linha 259:
  
 
Cálculo da onda em um tempo <math>t=t_f</math>:
 
Cálculo da onda em um tempo <math>t=t_f</math>:
 +
Lax-Friedrichs:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
  
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("lax.txt", "w+");
 +
 +
    int tmax, i, j, jmax;
 +
 +
//tamanho da corda: jmax-1
 +
    jmax = 50;
 +
 +
//u: posicao da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
 +
    //k = dt/dx
 +
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro;
 +
 +
//tmax: tempo final
 +
    tmax = 100;
 +
    k = 0.2;
 +
 +
 +
    //condicao inicial
 +
    for (j = 0 ; j < jmax ; j++)
 +
    {
 +
        u_now[j] = sin(M_PI*j/(jmax - 1));
 +
    }
 +
 +
    //condicao de contorno
 +
    u_old[0]=0;
 +
    u_old[jmax-1]=0;
 +
 +
    u_new[0] = 0;
 +
    u_new[jmax-1] = 0;
 +
 +
//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
    for (j = 1; j< jmax-1 ; j++)
 +
    {
 +
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
    }
 +
 +
//atualizacao da onda
 +
    for(t = 0 ; t < tmax ; t+=k)
 +
    {
 +
 +
        atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
        memcpy(u_old,u_now, sizeof(double)*jmax);
 +
        memcpy(u_now,u_new, sizeof(double)*jmax);
 +
    }
 +
 +
//onda no tempo t=tmax
 +
    for(j=0; j<jmax; j++)
 +
    {
 +
        fprintf(arq,"%d %lf\n", j, u_new[j]);
 +
    }
 +
 +
 +
    fclose(arq);
 +
}
 +
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
    //para j=1 e j=jmax-2 (penultimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posicoes ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
 +
    j=1;
 +
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] - u_old_[j]);
 +
 +
    for(j = 2 ; j < jmax-2 ; j++)
 +
    {
 +
        u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] + u_old_[j-2]);
 +
    }
 +
 +
    j=jmax-2;
 +
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (-u_old_[j] - 2 * u_old_[j] + u_old_[j-2]);
 +
 +
 +
 +
}
 +
 +
<source>
 +
 +
Lax-Wendroff:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("laxw.txt", "w+");
 +
 +
    int tmax,i,j,jmax;
 +
 +
//tamanho da corda: jmax-1
 +
    jmax = 50;
 +
 +
//u: posicao da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
    //k = dt/dx
 +
    double u_new[jmax],t,u_old[jmax],u_now[jmax],k,erro;
 +
 +
//tmax: tempo final
 +
    tmax = 100;
 +
    k = 0.2;
 +
 +
 +
    //condição inicial
 +
    for (j = 0 ; j < jmax ; j++)
 +
    {
 +
        u_now[j] = sin(M_PI*j/(jmax - 1));
 +
    }
 +
 +
    //condição de contorno
 +
    u_old[0] = 0;
 +
    u_old[jmax-1] = 0;
 +
 +
 +
    u_new[0] = 0;
 +
    u_new[jmax-1] = 0;
 +
 +
//cálculo de u para t=-dt, utilizando o método de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
    for (j = 1; j< jmax-1 ; j++)
 +
    {
 +
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
 +
    }
 +
 +
 +
//atualização da onda
 +
    for(t = 0 ; t < tmax ; t+=k)
 +
    {
 +
 +
        atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
        memcpy(u_old,u_now, sizeof(double)*jmax);
 +
        memcpy(u_now,u_new, sizeof(double)*jmax);
 +
    }
 +
 +
//onda no tempo t=tmax
 +
    for(j=0; j<jmax; j++)
 +
    {
 +
        fprintf(arq,"%d %lf\n", j, u_new[j]);
 +
    }
 +
 +
 +
    fclose(arq);
 +
 +
}
 +
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
    //para j=1 e j=jmax-2 (penúltimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posições ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
 +
    j=1;
 +
 +
    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] - 0.5 * u_old_[j] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
 +
    for(j = 2 ; j < jmax-2 ; j++)
 +
    {
 +
        u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
    }
 +
 +
    j=jmax-2;
 +
    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (-0.5 * u_old_[j] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
 +
 +
 +
}
 +
 +
<source>
 +
 +
Leapfrog:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("leapfrog.txt", "w+");
 +
 +
    int i, j, jmax;
 +
 +
    //tamanho da corda: jmax-1
 +
    jmax = 50;
 +
 +
    //u: posicao da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
    //k = dt/dx
 +
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro, tmax;
 +
 +
    //tmax: tempo final
 +
    tmax = 100;
 +
    k = 0.2;
 +
 +
    //condicao inicial
 +
    for (j = 0 ; j < jmax ; j++)
 +
    {
 +
        u_now[j] = sin(M_PI*j/(jmax - 1));
 +
    }
 +
 +
    //condicao de contorno
 +
    u_new[0] = 0;
 +
    u_new[jmax-1] = 0;
 +
 +
    u_old[0] = 0;
 +
    u_old[jmax-1] = 0;
 +
 +
    //calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
    for (j = 1; j< jmax-1 ; j++)
 +
    {
 +
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
    }
 +
 +
    //atualizacao da onda
 +
    for(t = 0 ; t < tmax ; t+=k)
 +
    {
 +
 +
 +
        atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
        memcpy(u_old,u_now, sizeof(double)*jmax);
 +
        memcpy(u_now,u_new, sizeof(double)*jmax);
 +
    }
 +
 +
    for(j=0; j<jmax; j++)
 +
    {
 +
        fprintf(arq,"%d %lf\n", j, u_new[j]);
 +
    }
 +
 +
 +
    fclose(arq);
 +
 +
}
 +
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
 +
    for(j = 1 ; j < jmax-1 ; j++)
 +
    {
 +
        u_new_[j] =  2 * u_now_[j] - u_old_[j] + pow(k,2) *( u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1] );
 +
    }
 +
 +
 +
}
 +
 +
<source>
  
 
Cálculo do erro:
 
Cálculo do erro:
  
 +
Lax-Friedrichs:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("erro_lax.dat", "w");
 +
 +
    int tmax, i, j, jmax;
 +
   
 +
    //tamanho da corda: jmax-1
 +
    jmax = 50;
 +
   
 +
    //u: posicao da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
    //k = dt/dx (aqui, dx = 1, k=dt)
 +
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro;
 +
   
 +
    //tmax: tempo final
 +
    tmax = 100;
 +
 +
//variamos o dt para fazer um grafico do erro em função de dt
 +
    int n=1;
 +
    while( n < 1200)
 +
    {
 +
        k = 0.001*n;
 +
 +
//condicao inicial
 +
        for (j = 0 ; j < jmax ; j++)
 +
        {
 +
            u_now[j] = sin(M_PI*j/(jmax - 1));
 +
        }
 +
       
 +
        //condicao de contorno
 +
        u_old[0]=0;
 +
        u_old[jmax-1]=0;
 +
       
 +
        u_new[0] = 0;
 +
u_new[jmax-1] = 0;
 +
       
 +
//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
        for (j = 1; j< jmax-1 ; j++)
 +
        {
 +
            u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
        }
 +
 +
//atualizacao da onda
 +
        for(t = 0 ; t < tmax ; t+=k)
 +
        {
 +
        //para que o ultimo tempo em que se calcula a posicao seja tmax, independentemente do valor de dt
 +
            if(t+k >tmax)
 +
            {
 +
                k = tmax -t;
 +
            }
 +
 +
            atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
            memcpy(u_old,u_now, sizeof(double)*jmax);
 +
            memcpy(u_now,u_new, sizeof(double)*jmax);
 +
        }
 +
 +
//calculo do erro
 +
        erro = 0;
 +
        for(j = 0 ; j < jmax ; j++)
 +
        {
 +
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
 +
            erro += fabs(analitica - u_now[j]);
 +
        }
 +
        erro = erro/jmax;
 +
       
 +
        fprintf(arq,"%.12lf %.12lf\n", n*0.001, erro);
 +
 +
 +
        n++;
 +
 +
    }
 +
 +
    fclose(arq);
 +
 +
}
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
//para j=1 e j=jmax-2 (penultimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posicoes ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
 +
j=1;
 +
u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] - u_old_[j]);
 +
 +
    for(j = 2 ; j < jmax-2 ; j++)
 +
    {
 +
        u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] + u_old_[j-2]);
 +
    }
 +
   
 +
    j=jmax-2;
 +
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (-u_old_[j] - 2 * u_old_[j] + u_old_[j-2]);
 +
 +
 +
 +
}
 +
 +
<source>
 +
 +
Lax-Wendroff:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("erro_laxw.dat", "w");
 +
 +
    int tmax,i,j,jmax;
 +
   
 +
    //tamanho da corda: jmax-1
 +
    jmax = 50;
 +
   
 +
    //u: posição da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
    //k = dt/dx (aqui, dx = 1, k=dt)
 +
    double u_new[jmax],t,u_old[jmax],u_now[jmax],k,erro;
 +
 +
//tmax: tempo final
 +
    tmax = 100;
 +
 +
 +
//variamos o dt para fazer um gráfico do erro em função de dt
 +
    int n=1;
 +
    while( n < 1200)
 +
    {
 +
        k = 0.001*n;
 +
 +
//condição inicial
 +
        for (j = 0 ; j < jmax ; j++)
 +
        {
 +
            u_now[j] = sin(M_PI*j/(jmax - 1));
 +
        }
 +
 +
//condição de contorno
 +
u_old[0] = 0;
 +
u_old[jmax-1] = 0;
 +
 +
u_new[0] = 0;
 +
u_new[jmax-1] = 0;
 +
 +
//cálculo de u para t=-dt, utilizando o método de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
        for (j = 1; j< jmax-1 ; j++)
 +
        {
 +
u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
 +
        }
 +
 +
 +
//atualização da onda
 +
        for(t = 0 ; t < tmax ; t+=k)
 +
        {
 +
        //para que o último tempo em que se calcula a posição seja tmax, independentemente do valor de dt
 +
            if(t+k >tmax)
 +
            {
 +
                k = tmax -t;
 +
            }
 +
 +
            atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
            memcpy(u_old,u_now, sizeof(double)*jmax);
 +
            memcpy(u_now,u_new, sizeof(double)*jmax);
 +
        }
 +
 +
//cálculo do erro
 +
        erro = 0;
 +
        for(j = 0 ; j < jmax ; j++)
 +
        {
 +
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
 +
            erro += fabs(analitica - u_now[j]);
 +
        }
 +
        erro = erro/jmax;
 +
     
 +
        fprintf(arq,"%.12lf %.12lf\n", n*0.001, erro);
 +
 +
 +
        n++;
 +
 +
    }
 +
 +
    fclose(arq);
 +
 +
}
 +
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
//para j=1 e j=jmax-2 (penúltimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posições ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
 +
j=1;
 +
 +
u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] - 0.5 * u_old_[j] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
 +
    for(j = 2 ; j < jmax-2 ; j++)
 +
    {
 +
        u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
    }
 +
   
 +
    j=jmax-2;
 +
    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (-0.5 * u_old_[j] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
 +
 +
 +
 +
}
 +
 +
 +
 +
<source>
 +
 +
Leapfrog:
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
 +
 +
void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("erro_leapfrog.dat", "w");
 +
 +
    int i, j, jmax;
 +
   
 +
    //tamanho da corda: jmax-1
 +
    jmax = 50;
 +
   
 +
    //u: posicao da corda
 +
/*    u_old em t-1    */
 +
/*    u_now em t      */
 +
/*    u_new em t+1    */
 +
    //k = dt/dx (aqui, dx = 1, k=dt)
 +
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro, tmax;
 +
 +
//tmax: tempo final
 +
    tmax = 100;
 +
 +
//variamos o dt para fazer um grafico do erro em função de dt
 +
    int n=1;
 +
    while( n < 1200)
 +
    {
 +
        k = 0.001*n;
 +
 +
//condicao inicial
 +
        for (j = 0 ; j < jmax ; j++)
 +
        {
 +
            u_now[j] = sin(M_PI*j/(jmax - 1));
 +
        }
 +
       
 +
//condicao de contorno
 +
u_new[0] = 0;
 +
u_new[jmax-1] = 0;
 +
 +
u_old[0] = 0;
 +
u_old[jmax-1] = 0;
 +
 +
//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
 +
        for (j = 1; j< jmax-1 ; j++)
 +
        {
 +
            u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
 +
        }
 +
 +
//atualizacao da onda
 +
        for(t = 0 ; t < tmax ; t+=k)
 +
        {
 +
        //para que o ultimo tempo em que se calcula a posicao seja tmax, independentemente do valor de dt
 +
            if(t+k >tmax)
 +
            {
 +
                k = tmax - t;
 +
            }
 +
           
 +
            atualizar_onda(u_new,u_now,u_old,jmax,k);
 +
 +
            memcpy(u_old,u_now, sizeof(double)*jmax);
 +
            memcpy(u_now,u_new, sizeof(double)*jmax);
 +
        }
 +
 +
//calculo do erro
 +
        erro = 0;
 +
        for(j = 0 ; j < jmax ; j++)
 +
        {
 +
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
 +
            erro += fabs(analitica - u_now[j]);
 +
        }
 +
        erro = erro/jmax;
 +
        fprintf(arq,"%.12lf %.12lf\n", n*0.001,erro);
 +
 +
 +
        n++;
 +
 +
    }
 +
 +
    fclose(arq);
 +
 +
}
 +
 +
 +
void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
 +
{
 +
    int j;
 +
 +
 +
    for(j = 1 ; j < jmax-1 ; j++)
 +
    {
 +
        u_new_[j] =  2 * u_now_[j] - u_old_[j] + pow(k,2) *( u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1] );
 +
    }
 +
 +
 +
}
 +
 +
<source>
  
 
'''Equação da onda em duas dimensões:'''
 
'''Equação da onda em duas dimensões:'''
 +
<source lang="c">
 +
#include<stdio.h>
 +
#include<math.h>
 +
#include<string.h>
 +
#include<stdlib.h>
 +
#define nx_ 71
 +
#define ny_ 71
 +
 +
double gauss( int x, int y, int tam);
 +
 +
double    H( int x, int y, int tam);
 +
 +
void atualizar_onda(double u_new[][ny_], double u_now[][ny_], double u_old[][ny_], double lambda[][ny_], double a,  double b,  double c, int nx, int ny, double rx, double ry);
 +
 +
double delta_u( double rx, double ry, double lambda[][ny_],  double u_now[][ny_], int i,  int j, int  im1, int ip1, int jm1, int jp1);
 +
 +
 +
 +
/*        META DADOS  */
 +
//
 +
/*    nx_ e ny_ , definidos acima por praticidade,    */
 +
/*    setam o tamanho dos vetores.                    */
 +
/*                                                    */
 +
/*    tmax  , tempo total da simulacao              */
 +
/*    rx e ry, dt/dx e dy/dt respectivamente          */
 +
/*    lambda , mapa do solo (profundidade em (x,y))  */
 +
//
 +
//
 +
/*    u representa a altura do mar em (x,y), sendo:  */
 +
//
 +
/*    u_old[x][y] em t = t-1    */
 +
/*    u_now[x][y] em t = t      */
 +
/*    u_new[x][y] em t = t+1    */
 +
//
 +
 +
 +
 +
void main()
 +
{
 +
 +
    FILE *arq;
 +
    arq = fopen("onda.txt", "w+");
 +
 +
 +
    int tmax, i, j, t, nx, ny;
 +
 +
    nx = nx_;
 +
    ny = ny_;
 +
    tmax = 300;
 +
 +
    double u_new[nx][ny], u_old[nx][ny], u_now[nx][ny], lambda[nx][ny], rx, ry;
 +
 +
    rx = 0.25;
 +
    ry = 0.25;
 +
 +
    //  incio loop da condição inicial,
 +
    //  laco duplo e usado para percorrer matriz nx*ny
 +
 +
    for(j = 0 ; j < ny  ; j++)
 +
    {
 +
        for(i = 0 ; i < nx ; i++)
 +
        {
 +
            /* u_now inicial em forma de sino */
 +
            u_now[i][j] = gauss(i,j,nx);
 +
            /* lambda inicial em forma de H() */
 +
            lambda[i][j] = H(i,j,nx);
 +
 +
        }
 +
    }
 +
 +
    //  fim loop da condição inicial
 +
 +
 +
    /*  calculo "sintetico" de u_old, pois a atualizacao nao e auto-iniciavel  */
 +
 +
    atualizar_onda(u_old, u_now, u_old, lambda, 0.5, 0, 0.5, nx, ny, rx, ry);
 +
 +
 +
    //inicio do laço temporal
 +
 +
    for(t = 0 ; t < tmax ; t++)
 +
    {
 +
 +
        //imprimindo no arquivo com laco duplo
 +
 +
 +
        /* calculam-se novos valores */
 +
 +
        atualizar_onda( u_new, u_now, u_old, lambda, 1, 1, 1, nx, ny, rx, ry);
 +
 +
 +
        /* matrizes antes novas se tornam antigas */
 +
        /*  u_old = u_now, u_now = u_new  */
 +
 +
 +
        memcpy(u_old,u_now, sizeof(double)*nx*ny);
 +
        memcpy(u_now,u_new, sizeof(double)*nx*ny);
 +
 +
 +
        /* OBS: Double tem o valor de 8 bytes na memoria. Como temos uma matriz de nx*ny, pegamos o tamanho*/
 +
        /* de um double e multiplicamos pela dimensao da matriz */
 +
        /* sintaxe memcpy(matriz a ser atualizada, matriz que passa o valor, tamanho em bytes da matriz)  */
 +
 +
    }
 +
 +
            for(j = 0 ; j < ny ; j++)
 +
        {
 +
            for(i = 0 ; i < nx  ; i++)
 +
            {
 +
                if(i == j){
 +
                fprintf(arq, "%d %d %lf\n", i, j, u_now[i][j]);
 +
                }
 +
            }
 +
        }
 +
 +
        /* Linhas em branco ao final de cada tempo para index do gnuplot */
 +
        fprintf(arq,"\n\n");
 +
 +
    fclose(arq);
 +
}
 +
 +
 +
 +
 +
 +
 +
double gauss(int x, int y,int tam)
 +
{
 +
    /* curva inicial em forma de sino*/
 +
 +
    double A, xc, yc, gauss, sigmax, sigmay;
 +
    //xc = (tam-1) / 2.;
 +
    //yc = (tam-1) / 2.;
 +
    xc = 0;
 +
    yc = 0;
 +
 +
    A = 1;
 +
    sigmax = 1;
 +
    sigmay = 1;
 +
 +
    gauss = A * exp(-0.5*pow(((x-xc)/sigmax),2) -0.5*pow(((y-yc)/sigmay),2));
 +
 +
    return gauss;
 +
}
 +
 +
 +
 +
 +
/* a funcao H corresponde ao formato do terreno, retorna a profundidade em relação a aguas calmas */
 +
 +
double H(int x, int y,int tam)
 +
{
 +
    /* curva para o formato do terreno em forma de sino virado*/
 +
    double A,xc,yc,h,sigmax,sigmay;
 +
    //xc = (tam-1) / 2.;
 +
    //yc = (tam-1) / 2.;
 +
 +
    A = 1;
 +
    sigmax = 1;
 +
    sigmay = 1;
 +
    xc = 0;
 +
    yc = 0;
 +
 +
    h = 1 - A * exp(-0.5*pow(((x-xc)/sigmax),2) -0.5*pow(((y-yc)/sigmay),2));
 +
 +
    return h;
 +
}
 +
 +
void atualizar_onda(double u_new[][ny_], double u_now[][ny_], double u_old[][ny_], double lambda[][ny_], double a,  double b,  double c, int nx, int ny, double rx, double ry)
 +
{
 +
// DOUBLE U_NEW[][NY_)] SINALIZA PARA O C QUE A FUNÇÃO RECEBERA UMA MATRIZ( TECNICAMENTE RECEBERA O ENDEREÇO NA MEMORIA DA MATRIZ) POR ISSO NÃO É NECESSARIO RETORNAR NENHUM VALOR
 +
// ESTA "TECNICA" É POSSIVEL POIS O NOME DA MATRIZ, NO CASO U_NEW, É NA VERDADE O ENDEREÇO DESSA MATRIZ NA MEMORIA. COMO ESTAMOS PASSANDO O ENDEREÇO NA MEMORIA, A FUNÇÃO CONSEGUE ALTERAR OS VALORES SEM NECESSIDADE DE RETORNO
 +
// PRECISAMOS DECLARAR O [NY_] NA FUNÇÃO POR QUESTÕES TECNICAS. MAS PENSEM NESSA SINTAXE COMO: PASSANDO O ENDEREÇO DA MATRIX PARA A FUNÇÃO, SEM NECESSIDADE DE RETORNO. A FUNÇÃO É LIVRE PARA EDITAR A PROPRIA MATRIZ
 +
 +
    int i,j;
 +
 +
    // LOOP DUPLO PARA ATUALIZAR AS PARTES INTERNAS DA MATRIZ
 +
    for(j = 1 ; j < ny - 1 ; j++)
 +
    {
 +
        for(i = 1 ; i < nx - 1  ; i++)
 +
 +
            // SEPAREI PARTE DA EQUAÇAO EM OUTRA FUNÇÃO PARA SIMPLIFICAR A VIDA. DELTA_U É SIMPLESMENTE UMA PARTE DA EQUAÇÃO ORIGINAL
 +
 +
            u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j-1,j+1);
 +
    }
 +
 +
    //PRECISAMOS AGORA ATUALIZAR AS LINHAS E COLUNAS EXTERNAS DA MATRIZ, POIS ESTAS NÃO FORAM INCLUIDAS NO LOOP ANTERIOR. ESTA AÇÃO NÃO ATUALIZA AS PONTAS, OU QUINAS, DA MATRIZ
 +
 +
 +
    i = 0; // ATUALiZANDO A PRIMEIRA COLUNA DA MATRIZ
 +
    for( j = 1; j < ny - 1  ; j++)
 +
    {
 +
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j-1,j+1);
 +
    }
 +
 +
    i = nx - 1;// ATUALZANDO A ULTIMA COLUNA DA MATRIZ
 +
    for( j = 1; j < ny - 1  ; j++)
 +
    {
 +
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j-1,j+1);
 +
    }
 +
 +
    // ---------------------- //
 +
 +
 +
    j = 0; // ATUALZANDO A PRIMEIRA LINHA DA MATRIZ
 +
    for( i = 1; i < nx - 1 ; i++)
 +
    {
 +
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j+1,j+1);
 +
 +
    }
 +
 +
 +
    j = ny - 1; // ATUALZANDO A ULTIMA LINHA DA MATRIZ
 +
    for( i = 1; i < nx - 1 ; i++)
 +
    {
 +
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j-1,j-1);
 +
 +
    }
 +
 +
 +
    // AGORA VAMOS ATUALIZAR as PONTAS DA MATRIZ. OU CANTOS, SE PREFERIR CHAMAR ASSIM
 +
 +
 +
    // PONTA [0][0]
 +
    i = 0;
 +
    j = 0;
 +
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j+1,j+1);
 +
 +
 +
    // PONTA [nx - 1][0]
 +
    i= nx - 1;
 +
    j= 0;
 +
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j+1,j+1);
 +
 +
 +
    // PONTA [0][ny -1]
 +
    i= 0;
 +
    j= ny - 1;
 +
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j-1,j-1);
 +
 +
 +
    // PONTA [NX-1][ny -1]
 +
    i= nx - 1;
 +
    j= ny - 1;
 +
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j-1,j-1);
 +
 +
 +
}
 +
 +
double delta_u( double rx, double ry, double lambda[][ny_],  double u_now[][ny_], int i,  int j, int  im1, int ip1, int jm1, int jp1)
 +
{
 +
    //CALCULAMOS AQUI  SEPARADO UMA PARTE DA EQUAÇÃO, POIS ELA MUDA DEPENDENDO DO QUE ESTAMOS CALCULANDO. SEJA UMA COLUNA INICIAL OU FINAL OU UM CANTO DA MATRIZ
 +
    //PARA ISSO COLOQUEI VALORES AUXILIARES DE IM1, IP1, JM1, JP1 . P DE PLUS E M DE MINUS.POIS ESTES VALORES SAO TROCADOS EM VARIAS PARTES
 +
 +
    return (
 +
              pow(rx,2) * ( ((0.5 * (lambda[ip1][j] + lambda[i][j])) * (u_now[ip1][j] - u_now[i][j]))
 +
                            -  ((0.5 * (lambda[i][j] + lambda[im1][j])) * (u_now[i][j] - u_now[im1][j])))
 +
 +
 +
              + pow(ry,2) * ( ((0.5 * (lambda[i][jp1] + lambda[i][j])) * (u_now[i][jp1] - u_now[i][j]))
 +
                              -  ((0.5 * (lambda[i][j] + lambda[i][jm1])) * (u_now[i][j] - u_now[i][jm1]))));
 +
 +
}
 +
 +
<source>
  
 
==Bibliografia==
 
==Bibliografia==
 
<references/>
 
<references/>

Edição das 22h00min de 26 de novembro de 2017

Integrantes do grupo: Rodrigo Zamin Ferreira (262692), Leonardo Xavier Rodrigues (262696), Maurício Gomes de Queiroz (264889) e Rodrigo Lopes de Sousa Silva (262705)

Introdução

A modelagem numérica vem se tornando cada vez mais uma ferramenta indispensável para um engenheiro. Tal modelagem pode trazer informações importantes para entender como melhor abordar o desenvolvimento de um projeto, neste caso, um que envolva ondas. Nós, como futuros engenheiros físicos, pensamos em trazer um problema mais "concreto", de engenharia costeira e portuária, que pode ou não surgir em nossas vidas profissionais mas cujo método de solução certamente estará presente. Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda.

Inicialmente, para testarmos os diferentes métodos, utilizaremos a equação da onda em uma dimensão, que é uma equação diferencial parcial de segunda ordem, para modelarmos uma corda:

em que é o deslocamento vertical da corda, é a velocidade de propagação da onda e , com o comprimento da corda.

Podemos reescrever a equação da seguinte forma:

.

Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição e , de forma que:

Aqui usaremos , sem perda de generalidade. As condições de contorno utilizadas aqui são (pontas fixas), e as condições iniciais são e

Algoritmos

Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, corresponde à posição, e representa o tempo.

Método de Lax-Friedrichs

Esse método de ordem [1] consiste em inicialmente discretizar as equações no esquema FTCS (Forward Time Centered Space), ou seja, discretizando a derivada temporal utilizando os tempos e e a derivada espacial através das posições e :

,


.

Resultando em

,


.

Entretanto, ao se realizar uma análise de estabilidade de Von Neumann, conclui-se que esse método é instável[1] . Para torná-lo estável, é necessário trocarmos os termos e por suas médias espaciais, chegando, assim, na expressão do esquema de Lax-Friedrichs:


,


.

Para obtermos o valor de , que é o nosso objetivo, discretizamos a equação

,

Embora as médias espaciais sejam necessárias para a estabilidade do método, elas introduzem um problema: surge um efeito chamado de dissipação numérica, ou seja, a amplitude da solução diminui com o tempo. Isso pode ser observado através da análise de Von Neumann ou de uma investigação da equação do esquema Lax-Friedrichs [1] . Por este método, observa-se que ao inserirmos as médias, mudamos a equação original do problema, pois agora há também um termo do tipo difusivo (uma derivada segunda), com constante de difusão [1].

Agora vamos unir todas as equações, utilizando, além da equação para obtida acima, as discretizações de e

,


.

Assim, obtemos

.

Método de Leapfrog

Neste método , de ordem [1], utilizamos os pontos intermediários na discretização das equações.

Para temos

,


Para temos

,


Para temos

,


Utilizando o fato de que

,


,

chegamos na equação para


,

o que é equivalente a discretizarmos a equação da onda diretamente, utilizando que, para uma função ,

,

sendo a discretização em .

Método de Lax-Wendroff de Dois Passos

Para este método, de ordem , o primeiro passo consiste em calcular o valor de e utilizando o método de Lax-Friedrichs, para posterior cálculo de e :

,


,


,


,


Agora, no tempo :

,


,


Agrupando as equações,

,


,

E finalmente temos a equação unificada em u, utilizando a expressão para e as discretizações de e , como obtidas na seção sobre o Método de Lax-Friedrichs:

,

Implementação

Ao implementarmos o método, surgem dois problemas: o problema não é auto-inicializável, pois para calcularmos o valor de , necessitamos de (além de ). Entretanto, isto é rapidamente solucionado quando discretizamos a condição inicial de que :

,

ou seja, para o cálculo de , utilizamos que . Através do método de Leapfrog, dessa forma conseguimos isolar :


,


.

Porém, isso não ocorre com os outros dois métodos, pois surgem termos em diferentes posições para o tempo (de , , até ), sendo necessário resolvermos o sistema como um todo simultaneamente, ou seja, teríamos que inverter uma matriz. Por isso, foi utilizado o método de Leapfrog para o cálculo de em todos os métodos, devido a sua simplicidade.

Além disso, são necessários valores de e de , com correspondendo a , para calcularmos e , para qualquer tempo, utilizando os métodos de Lax-Wendroff de dois passos e Lax-Friedrichs. A solução a este problema foi utilizarmos

.

Pensando na condição inicial , e estendendo para além da corda (pensando no seno de ), observamos que ela respeita as equações acima.

Solução e Análise de erros

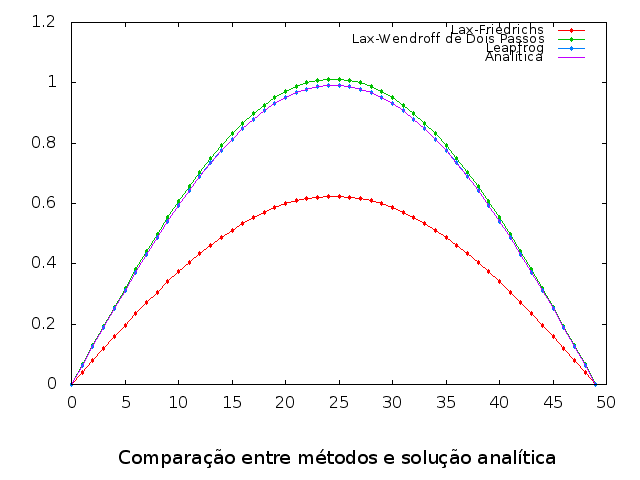
Primeiramente, apresentamos abaixo as soluções geradas pelos programas, em comparação com a solução analítica.

Comparação da solução analítica com as soluções numéricas

Aqui já podemos observar o que foi comentado na seção sobre o método de Lax-Friedrichs: devido à dissipação numérica inerente ao método, há uma diminuição da amplitude da onda ao longo do tempo, embora ela mantenha sua forma. Isso interferirá na análise do erro deste método, o que será apresentado na sequência.


A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração. Nesse caso, a solução é [2].A análise de erros se torna mais evidente durante a escolha do parâmetro , onde . Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro).

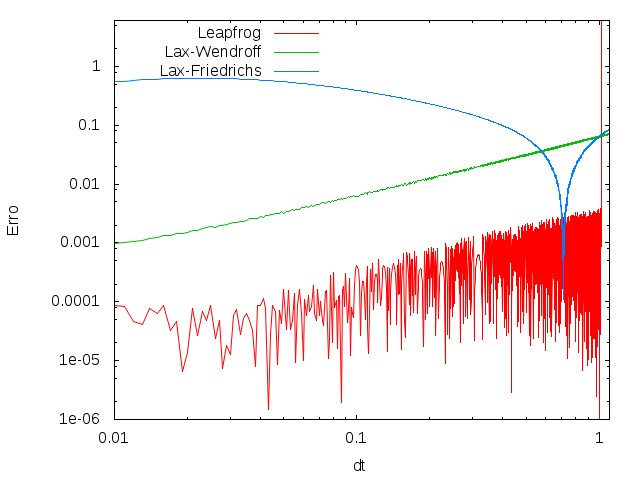
O erro foi obtido efetuando uma média espacial, ou seja, o programa foi evoluindo até um tempo final , e, em , foi feita uma média sobre o valor absoluto da diferença entre a solução analítica e a numérica. Aqui variamos o valor de , fixando , de forma que .

Comparação do erro global entre os três métodos estudados com escala logarítimica em ambos os eixos

Podemos observar que os erros crescem à medida que o parâmetro k se torna maior, como seria de se esperar.

Além disso, sabendo a ordem do erro dos métodos, podemos determinar a inclinação da reta que melhor se ajusta aos pontos. Se um método tem erro de ordem ,

em que é o erro local, ou seja, o erro de um passo do método, e é uma constante. Assim, o erro global , ou seja, o erro após N passos, é dado por

Como , . Logo, se o erro local é de ordem , o erro global (que é o que calculamos aqui) é de ordem . Além disso, como utilizamos escala logarítmica para representar os resultados, a função do erro global se torna

Ou seja, a inclinação do gráfico do erro global é .

Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação aproximada de 1, já que os métodos são de ordem . Com relação ao gráfico do erro do método de Lax-Friedrichs, é mais complicado de fazer sua análise, uma vez que há o efeito de dissipação numérica, que se intensifica para valores menores de . Podemos observar nos dados que o ponto de máximo na parte esquerda do gráfico corresponde a um erro de aproximadamente , que é a média da solução analítica no tempo (conforme solução analítica, a amplitude no tempo é , e a média de vale ). Isso significa que, devido à dissipação, a solução numérica é praticamente 0 frente à solução analítica na parte esquerda do gráfico.

Simulação de Propagação de Onda 2D no Mar Dependente de Topografia

O modelo mais simples para a propagação de onda dependente da topografia parte da equação da onda [3] [4], incluindo uma velocidade dependente da posição, da forma .

,


Sendo uma representação da profundidade em águas calmas, a aceleração da gravidade e a elevação da água em relação ao nível de águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar. A dependência em de permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas. Entretanto, utilizaremos aqui , sem dependência no tempo, e mudaremos as condições iniciais para a modelagem do problema, além de usarmos , para simplificarmos as expressões.

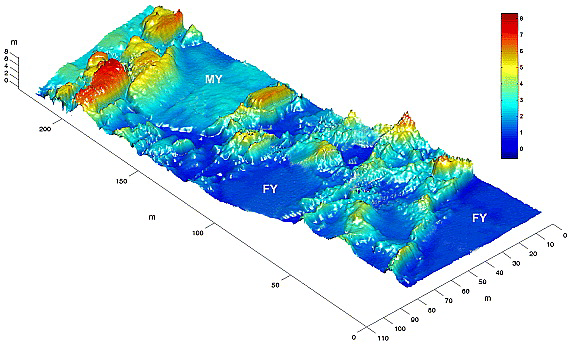
Exemplo de mapeamento de terreno sub - calota polar feito por AUV (autonomous underwater vehicle)[5]

Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Pode ser mostrado que a velocidade da onda pode ser dada por , para o caso em que , o que é razoável para um tsunami, que tem um comprimento de onda da ordem de até centenas de quilômetros, com uma profundidade da ordem de quilômetros[6]. Como o período da onde não se altera [6], quanto menor a profundidade, menor a velocidade, e menor o seu comprimento de onda. Além disso, devido à conservação de energia, e supondo que a extensão da frente de onda não seja alterada, é obtida a chamada Lei de Green[6]:

em que é a amplitude da onda, e os índices representando dois meios. Logo, quanto menos profundo, maior a amplitude da onda. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem. Nos gráficos abaixo podemos observar esses efeitos.

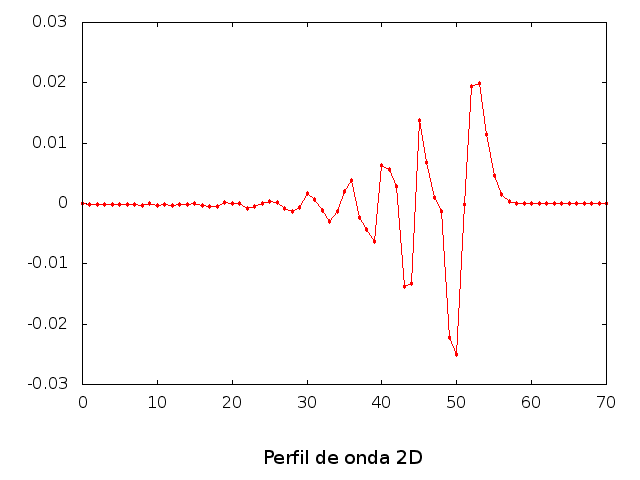
Pontos visitados por simulação em 1D

E no caso em que simulamos uma fina camada de líquido, podemos ver a diminuição de velocidade da onda e o aumento de sua amplitude, especialmente no trecho mais à esquerda:


Simulação em 1D de ondas perto da margem, com camada fina de líquido

É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro.

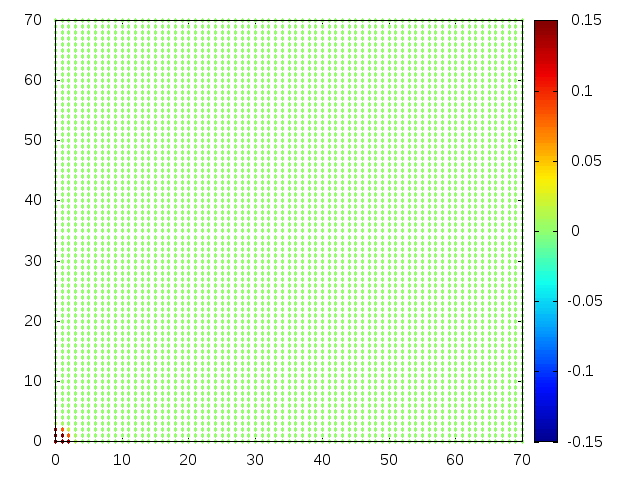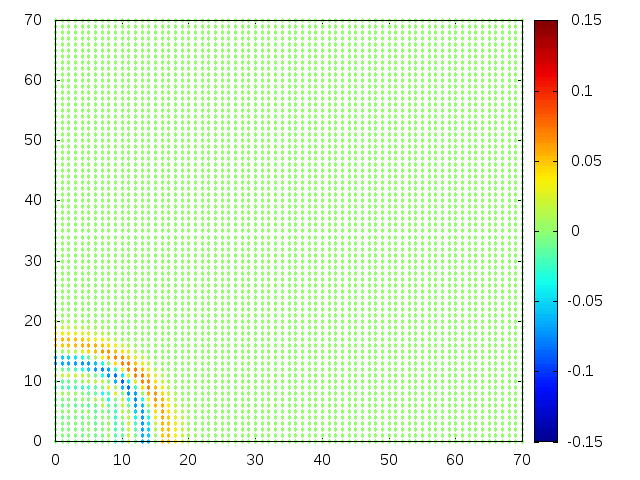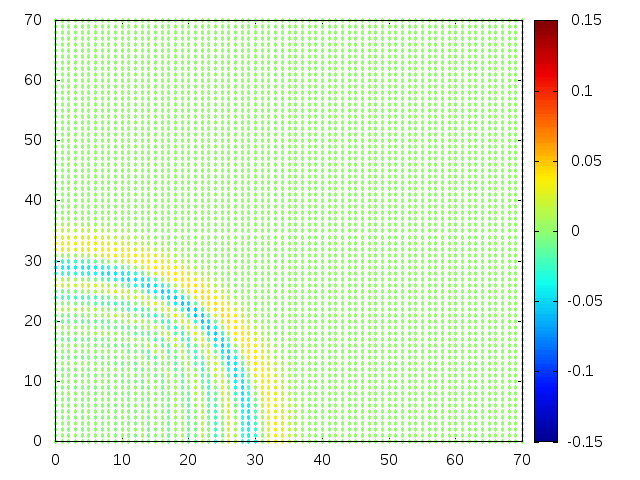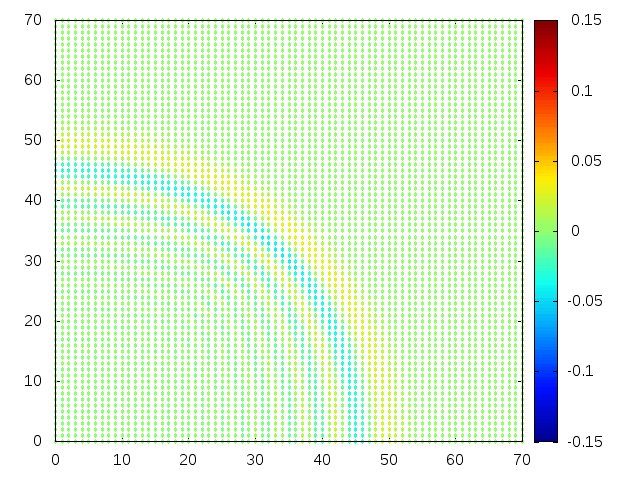
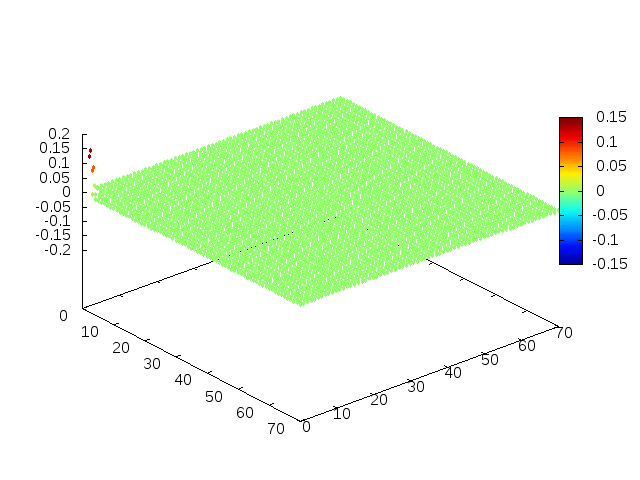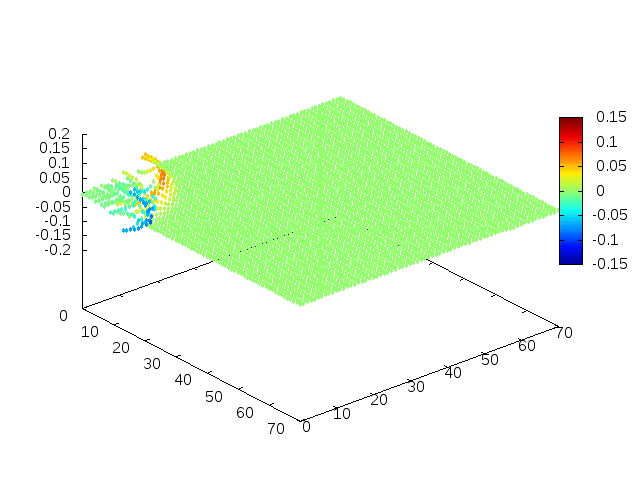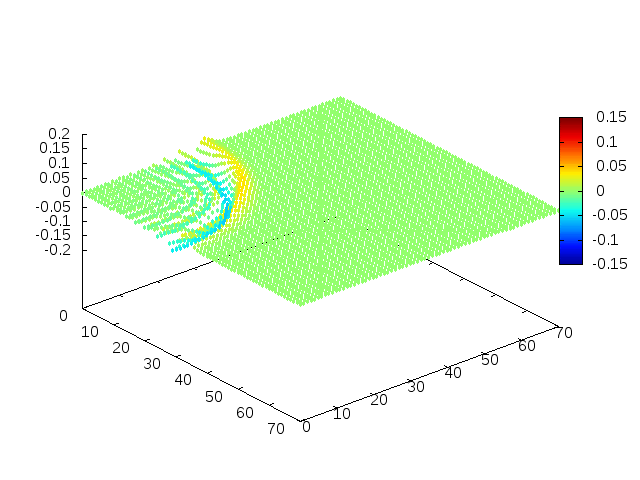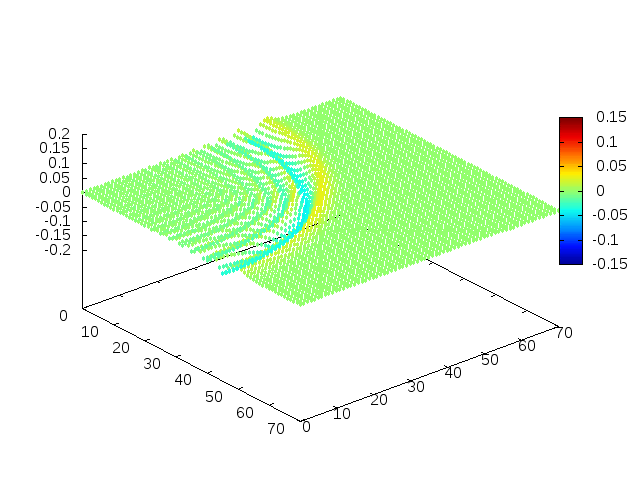
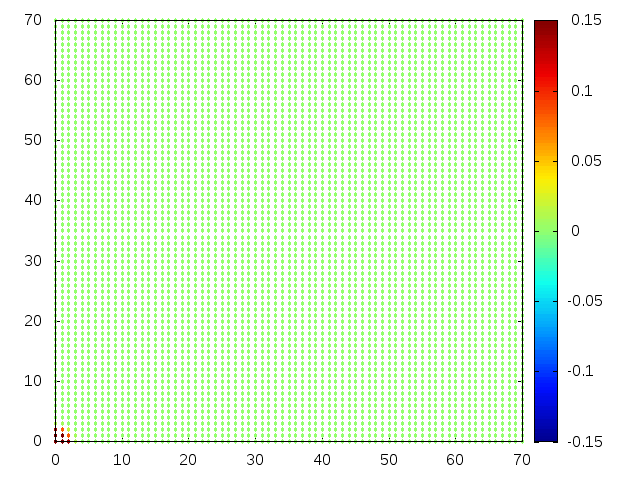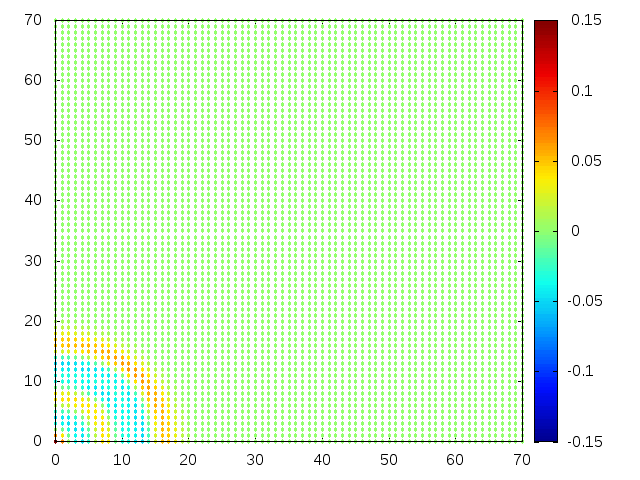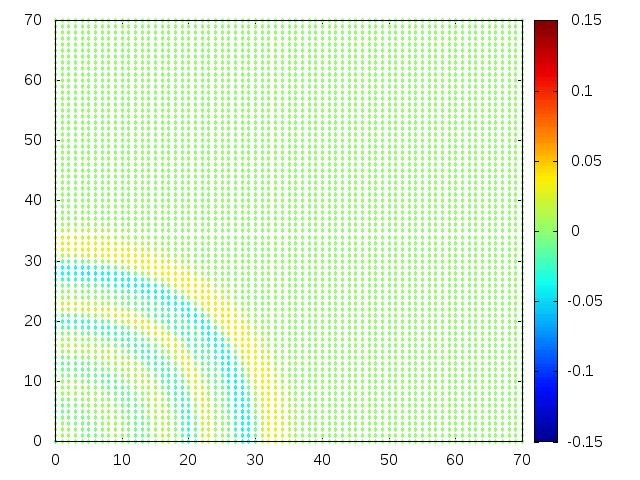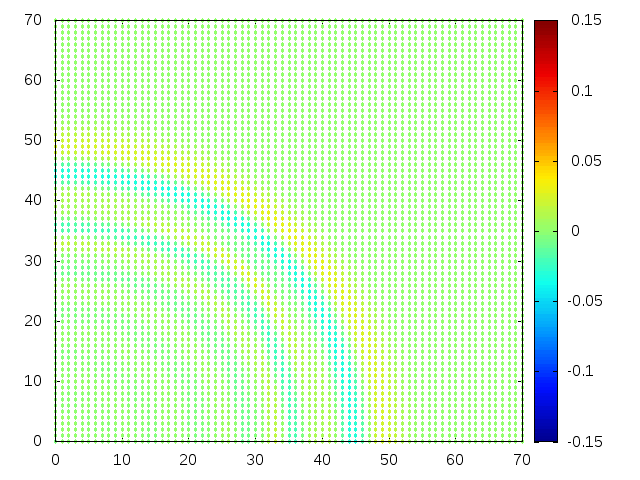
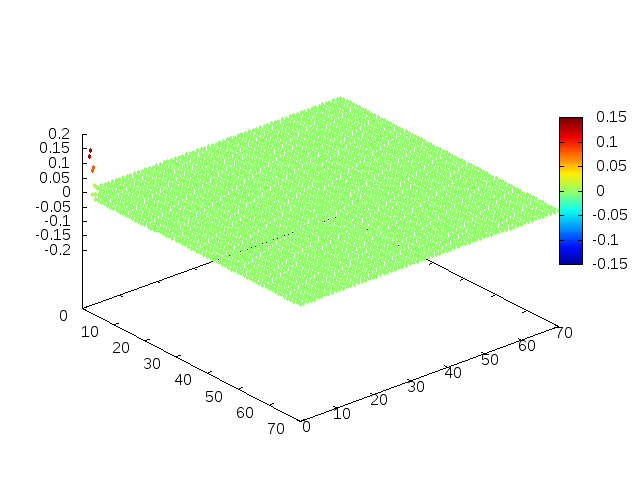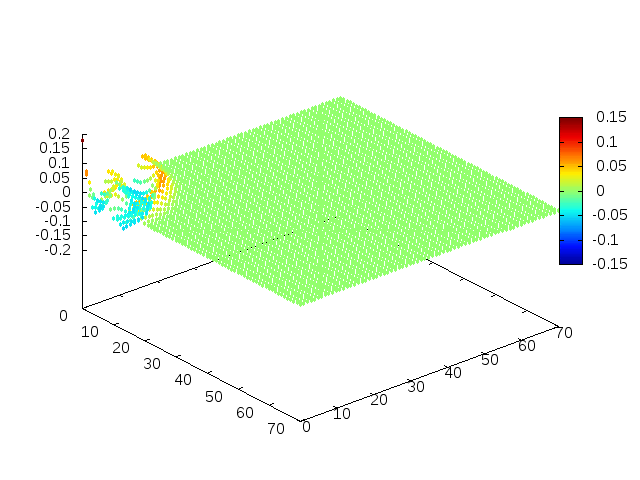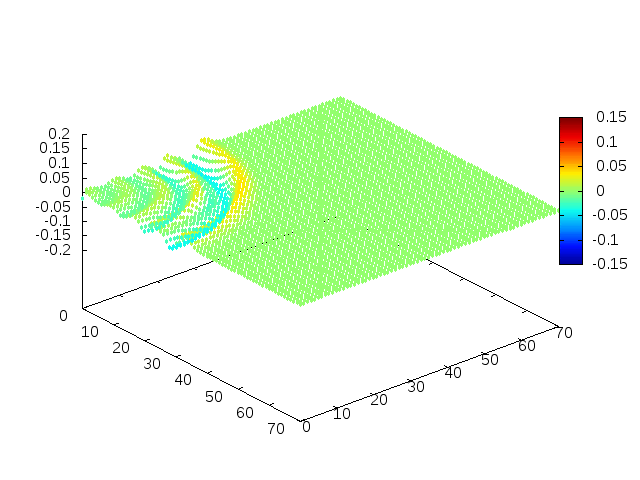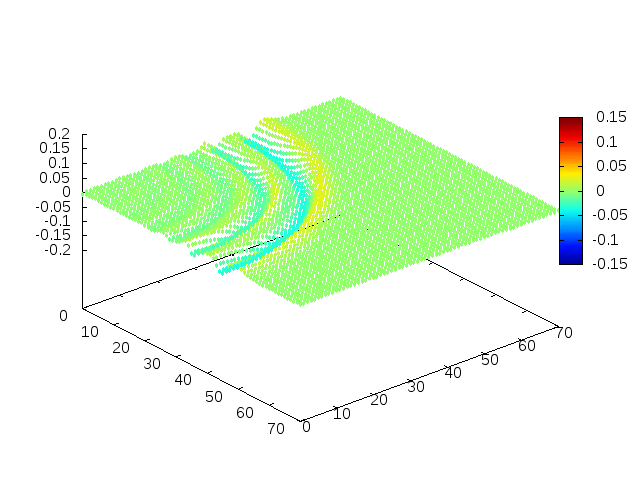
Estendendo o algoritmo de Leapfrog à situação 2D, obtemos, para uma condição inicial de uma gaussiana com média 0 e desvio padrão 1, tanto em quanto em , e :

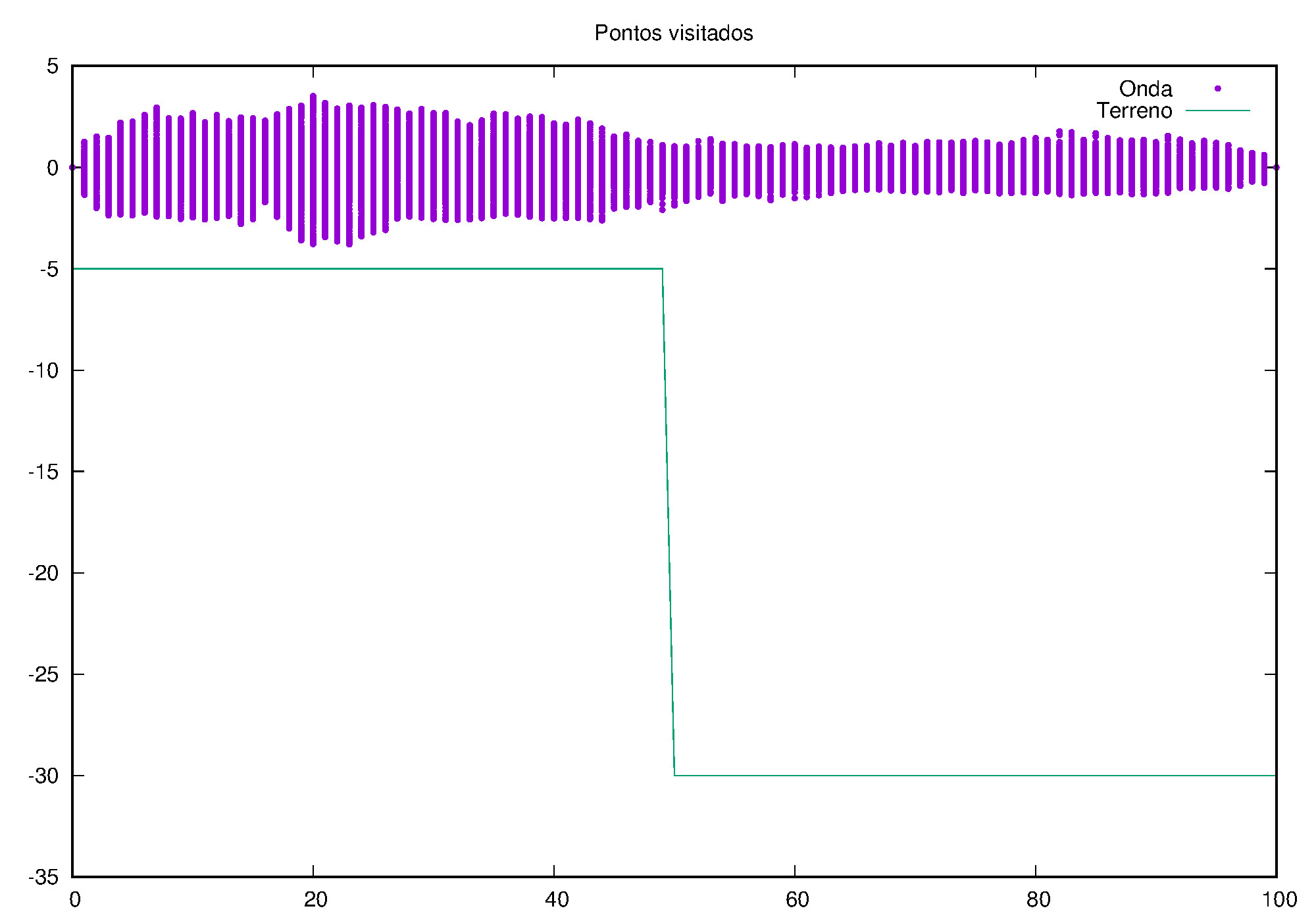
Simulação em 2D de ondas em águas com profundidade constante, visão de cima
Simulação em 2D de onda em águas com profundidade constante, visão em ângulo


Podemos então, analisar como a mesma condição inicial se porta quando , simulando uma elevação de terra:


Simulação em 2D de ondas em águas com gaussiana na origem, visão de cima
Simulação em 2D de onda em águas com gaussiana na origem, visão em ângulo

Perfil da onda em sua diagonal:

Perfil da onda em sua diagonal no tempo de simulação igual a 300

Programas

Equação da onda em uma dimensão:

Cálculo da onda em um tempo : Lax-Friedrichs: 

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("lax.txt", "w+");

    int tmax, i, j, jmax;
	
	//tamanho da corda: jmax-1
    jmax = 50;

	//u: posicao da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */

    //k = dt/dx
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro;

	//tmax: tempo final
    tmax = 100;
    k = 0.2;


    //condicao inicial
    for (j = 0 ; j < jmax ; j++)
    {
        u_now[j] = sin(M_PI*j/(jmax - 1));
    }

    //condicao de contorno
    u_old[0]=0;
    u_old[jmax-1]=0;

    u_new[0] = 0;
    u_new[jmax-1] = 0;

	//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
    for (j = 1; j< jmax-1 ; j++)
    {
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
    }

	//atualizacao da onda
    for(t = 0 ; t < tmax ; t+=k)
    {

        atualizar_onda(u_new,u_now,u_old,jmax,k);

        memcpy(u_old,u_now, sizeof(double)*jmax);
        memcpy(u_now,u_new, sizeof(double)*jmax);
    }

	//onda no tempo t=tmax
    for(j=0; j<jmax; j++)
    {
        fprintf(arq,"%d %lf\n", j, u_new[j]);
    }


    fclose(arq);
}


void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;

    //para j=1 e j=jmax-2 (penultimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posicoes ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
    j=1;
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] - u_old_[j]);

    for(j = 2 ; j < jmax-2 ; j++)
    {
        u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] + u_old_[j-2]);
    }

    j=jmax-2;
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (-u_old_[j] - 2 * u_old_[j] + u_old_[j-2]);



}

<source>

Lax-Wendroff:
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("laxw.txt", "w+");

    int tmax,i,j,jmax;

	//tamanho da corda: jmax-1
    jmax = 50;

	//u: posicao da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */
    //k = dt/dx
    double u_new[jmax],t,u_old[jmax],u_now[jmax],k,erro;

	//tmax: tempo final
    tmax = 100;
    k = 0.2;


    //condição inicial
    for (j = 0 ; j < jmax ; j++)
    {
        u_now[j] = sin(M_PI*j/(jmax - 1));
    }

    //condição de contorno
    u_old[0] = 0;
    u_old[jmax-1] = 0;


    u_new[0] = 0;
    u_new[jmax-1] = 0;

//cálculo de u para t=-dt, utilizando o método de leapfrog - aqui usamos que du/dt = 0 em t=0
    for (j = 1; j< jmax-1 ; j++)
    {
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);

    }


//atualização da onda
    for(t = 0 ; t < tmax ; t+=k)
    {

        atualizar_onda(u_new,u_now,u_old,jmax,k);

        memcpy(u_old,u_now, sizeof(double)*jmax);
        memcpy(u_now,u_new, sizeof(double)*jmax);
    }

	//onda no tempo t=tmax
    for(j=0; j<jmax; j++)
    {
        fprintf(arq,"%d %lf\n", j, u_new[j]);
    }


    fclose(arq);

}


void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;

    //para j=1 e j=jmax-2 (penúltimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posições ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
    j=1;

    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] - 0.5 * u_old_[j] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);

    for(j = 2 ; j < jmax-2 ; j++)
    {
        u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
    }

    j=jmax-2;
    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (-0.5 * u_old_[j] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);



}

<source>

Leapfrog:
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("leapfrog.txt", "w+");

    int i, j, jmax;

    //tamanho da corda: jmax-1
    jmax = 50;

    //u: posicao da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */
    //k = dt/dx
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro, tmax;

    //tmax: tempo final
    tmax = 100;
    k = 0.2;

    //condicao inicial
    for (j = 0 ; j < jmax ; j++)
    {
        u_now[j] = sin(M_PI*j/(jmax - 1));
    }

    //condicao de contorno
    u_new[0] = 0;
    u_new[jmax-1] = 0;

    u_old[0] = 0;
    u_old[jmax-1] = 0;

    //calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
    for (j = 1; j< jmax-1 ; j++)
    {
        u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
    }

    //atualizacao da onda
    for(t = 0 ; t < tmax ; t+=k)
    {


        atualizar_onda(u_new,u_now,u_old,jmax,k);

        memcpy(u_old,u_now, sizeof(double)*jmax);
        memcpy(u_now,u_new, sizeof(double)*jmax);
    }

    for(j=0; j<jmax; j++)
    {
        fprintf(arq,"%d %lf\n", j, u_new[j]);
    }


    fclose(arq);

}


void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;


    for(j = 1 ; j < jmax-1 ; j++)
    {
        u_new_[j] =   2 * u_now_[j] - u_old_[j] + pow(k,2) *( u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1] );
    }


}

<source>

Cálculo do erro:

Lax-Friedrichs:
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("erro_lax.dat", "w");

    int tmax, i, j, jmax;
    
    //tamanho da corda: jmax-1
    jmax = 50; 
    
    //u: posicao da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */
    //k = dt/dx (aqui, dx = 1, k=dt)
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro;
    
    //tmax: tempo final
    tmax = 100;

	//variamos o dt para fazer um grafico do erro em função de dt
    int n=1;
    while( n < 1200)
    {
        k = 0.001*n;

		//condicao inicial
        for (j = 0 ; j < jmax ; j++)
        {
            u_now[j] = sin(M_PI*j/(jmax - 1));
        }
        
        //condicao de contorno
        u_old[0]=0;
        u_old[jmax-1]=0;
        
        u_new[0] = 0;
		u_new[jmax-1] = 0;
        
		//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
        for (j = 1; j< jmax-1 ; j++)
        {
            u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
        }

		//atualizacao da onda	
        for(t = 0 ; t < tmax ; t+=k)
        {
        	//para que o ultimo tempo em que se calcula a posicao seja tmax, independentemente do valor de dt
            if(t+k >tmax)
            {
                k = tmax -t;
            }

            atualizar_onda(u_new,u_now,u_old,jmax,k);

            memcpy(u_old,u_now, sizeof(double)*jmax);
            memcpy(u_now,u_new, sizeof(double)*jmax);
        }

		//calculo do erro
        erro = 0;
        for(j = 0 ; j < jmax ; j++)
        {
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
            erro += fabs(analitica - u_now[j]);
        }
        erro = erro/jmax;
        
        fprintf(arq,"%.12lf %.12lf\n", n*0.001, erro);


        n++;

    }

    fclose(arq);

}

void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;

	//para j=1 e j=jmax-2 (penultimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posicoes ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
	j=1;
	u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] - u_old_[j]);

    for(j = 2 ; j < jmax-2 ; j++)
    {
        u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (u_old_[j+2] - 2 * u_old_[j] + u_old_[j-2]);
    }
    
    j=jmax-2;
    u_new_[j] = u_now_[j] + 0.5 * (u_now_[j-1] + u_now_[j+1]) - 0.5 * (u_old_[j-1] + u_old_[j+1]) + 0.25 * pow(k,2) * (-u_old_[j] - 2 * u_old_[j] + u_old_[j-2]);



}

<source>

Lax-Wendroff:
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("erro_laxw.dat", "w");

    int tmax,i,j,jmax;
    
    //tamanho da corda: jmax-1
    jmax = 50;
    
    //u: posição da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */
    //k = dt/dx (aqui, dx = 1, k=dt)
    double u_new[jmax],t,u_old[jmax],u_now[jmax],k,erro;

	//tmax: tempo final
    tmax = 100;


	//variamos o dt para fazer um gráfico do erro em função de dt
    int n=1;
    while( n < 1200)
    {
        k = 0.001*n;
		
		//condição inicial
        for (j = 0 ; j < jmax ; j++)
        {
            u_now[j] = sin(M_PI*j/(jmax - 1));
        }

		//condição de contorno
		u_old[0] = 0;
		u_old[jmax-1] = 0;
		
		u_new[0] = 0;
		u_new[jmax-1] = 0;
		
		//cálculo de u para t=-dt, utilizando o método de leapfrog - aqui usamos que du/dt = 0 em t=0
        for (j = 1; j< jmax-1 ; j++)
        {
			u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);

        }


		//atualização da onda
        for(t = 0 ; t < tmax ; t+=k)
        {
        	//para que o último tempo em que se calcula a posição seja tmax, independentemente do valor de dt
            if(t+k >tmax)
            {
                k = tmax -t;
            }

            atualizar_onda(u_new,u_now,u_old,jmax,k);

            memcpy(u_old,u_now, sizeof(double)*jmax);
            memcpy(u_now,u_new, sizeof(double)*jmax);
        }

		//cálculo do erro
        erro = 0;
        for(j = 0 ; j < jmax ; j++)
        {
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
            erro += fabs(analitica - u_now[j]);
        }
        erro = erro/jmax;
      
        fprintf(arq,"%.12lf %.12lf\n", n*0.001, erro);


        n++;

    }

    fclose(arq);

}


void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;

	//para j=1 e j=jmax-2 (penúltimas posições), necessitamos de u em x=-1 e x=jmax, respectivamente, sendo que essas posições ficam fora do vetor (vai de 0 a jmax-1). Aqui, foi feito u(x=-1)=-u(x=1) e u(x=jmax)=-u(x=jmax-2)
	j=1;
	
	u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] - 0.5 * u_old_[j] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);

    for(j = 2 ; j < jmax-2 ; j++)
    {
        u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (0.5 * u_old_[j+2] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);
    }
    
    j=jmax-2;
    u_new_[j] = 2 * u_now_[j] - u_old_[j] + 0.5 * pow(k,2) * (-0.5 * u_old_[j] - u_old_[j+1] + u_old_[j] - u_old_[j-1] + 0.5 * u_old_[j-2] + u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1]);



}



<source>

Leapfrog:
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>


void atualizar_onda(double u_new[],double u_now[],double u_old[],int jmax,double k);

void main()
{

    FILE *arq;
    arq = fopen("erro_leapfrog.dat", "w");

    int i, j, jmax;
    
    //tamanho da corda: jmax-1
    jmax = 50;
    
    //u: posicao da corda
	/*    u_old em t-1    */
	/*    u_now em t      */
	/*    u_new em t+1    */
    //k = dt/dx (aqui, dx = 1, k=dt)
    double u_new[jmax], t, u_old[jmax], u_now[jmax], k, erro, tmax;

	//tmax: tempo final
    tmax = 100;

	//variamos o dt para fazer um grafico do erro em função de dt
    int n=1;
    while( n < 1200)
    {
        k = 0.001*n;

		//condicao inicial
        for (j = 0 ; j < jmax ; j++)
        {
            u_now[j] = sin(M_PI*j/(jmax - 1));
        }
        
		//condicao de contorno
		u_new[0] = 0;
		u_new[jmax-1] = 0;
		
		u_old[0] = 0;
		u_old[jmax-1] = 0;
		
		//calculo de u para t=-dt, utilizando o metodo de leapfrog - aqui usamos que du/dt = 0 em t=0
        for (j = 1; j< jmax-1 ; j++)
        {
            u_old[j] = u_now[j] + 0.5 * pow(k,2) * (u_now[j+1] - 2 * u_now[j] + u_now[j-1]);
        }

		//atualizacao da onda
        for(t = 0 ; t < tmax ; t+=k)
        {
        	//para que o ultimo tempo em que se calcula a posicao seja tmax, independentemente do valor de dt
            if(t+k >tmax)
            {
                k = tmax - t;
            }
            
            atualizar_onda(u_new,u_now,u_old,jmax,k);

            memcpy(u_old,u_now, sizeof(double)*jmax);
            memcpy(u_now,u_new, sizeof(double)*jmax);
        }

		//calculo do erro
        erro = 0;
        for(j = 0 ; j < jmax ; j++)
        {
            double analitica = cos((M_PI*t)/(jmax - 1))*sin((M_PI*j)/(jmax - 1));
            erro += fabs(analitica - u_now[j]);
        }
        erro = erro/jmax;
        fprintf(arq,"%.12lf %.12lf\n", n*0.001,erro);


        n++;

    }

    fclose(arq);

}


void atualizar_onda(double u_new_[],double u_now_[],double u_old_[],int jmax,double k)
{
    int j;


    for(j = 1 ; j < jmax-1 ; j++)
    {
        u_new_[j] =   2 * u_now_[j] - u_old_[j] + pow(k,2) *( u_now_[j+1] - 2 * u_now_[j] + u_now_[j-1] );
    }


}

<source>

'''Equação da onda em duas dimensões:'''
<source lang="c">
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#define nx_ 71
#define ny_ 71

double gauss( int x, int y, int tam);

double     H( int x, int y, int tam);

void atualizar_onda(double u_new[][ny_], double u_now[][ny_], double u_old[][ny_], double lambda[][ny_], double a,  double b,  double c, int nx, int ny, double rx, double ry);

double delta_u( double rx, double ry, double lambda[][ny_],  double u_now[][ny_], int i,  int j, int  im1, int ip1, int jm1, int jp1);



/*        META DADOS   */
//
/*    nx_ e ny_ , definidos acima por praticidade,    */
/*    setam o tamanho dos vetores.                    */
/*                                                    */
/*    tmax   , tempo total da simulacao               */
/*    rx e ry, dt/dx e dy/dt respectivamente          */
/*    lambda , mapa do solo (profundidade em (x,y))   */
//
//
/*     u representa a altura do mar em (x,y), sendo:  */
//
/*    u_old[x][y] em t = t-1    */
/*    u_now[x][y] em t = t      */
/*    u_new[x][y] em t = t+1    */
//



void main()
{

    FILE *arq;
    arq = fopen("onda.txt", "w+");


    int tmax, i, j, t, nx, ny;

    nx = nx_;
    ny = ny_;
    tmax = 300;

    double u_new[nx][ny], u_old[nx][ny], u_now[nx][ny], lambda[nx][ny], rx, ry;

    rx = 0.25;
    ry = 0.25;

    //   incio loop da condição inicial,
    //   laco duplo e usado para percorrer matriz nx*ny

    for(j = 0 ; j < ny  ; j++)
    {
        for(i = 0 ; i < nx ; i++)
        {
            /* u_now inicial em forma de sino */
            u_now[i][j] = gauss(i,j,nx);
            /* lambda inicial em forma de H() */
            lambda[i][j] = H(i,j,nx);

        }
    }

    //   fim loop da condição inicial


    /*  calculo "sintetico" de u_old, pois a atualizacao nao e auto-iniciavel  */

    atualizar_onda(u_old, u_now, u_old, lambda, 0.5, 0, 0.5, nx, ny, rx, ry);


    //inicio do laço temporal

    for(t = 0 ; t < tmax ; t++)
    {

        //imprimindo no arquivo com laco duplo


        /* calculam-se novos valores */

        atualizar_onda( u_new, u_now, u_old, lambda, 1, 1, 1, nx, ny, rx, ry);


        /* matrizes antes novas se tornam antigas */
        /*   u_old = u_now, u_now = u_new   */


        memcpy(u_old,u_now, sizeof(double)*nx*ny);
        memcpy(u_now,u_new, sizeof(double)*nx*ny);


        /* OBS: Double tem o valor de 8 bytes na memoria. Como temos uma matriz de nx*ny, pegamos o tamanho*/
        /* de um double e multiplicamos pela dimensao da matriz */
        /* sintaxe memcpy(matriz a ser atualizada, matriz que passa o valor, tamanho em bytes da matriz)  */

    }

            for(j = 0 ; j < ny ; j++)
        {
            for(i = 0 ; i < nx  ; i++)
            {
                if(i == j){
                fprintf(arq, "%d %d %lf\n", i, j, u_now[i][j]);
                }
            }
        }

        /* Linhas em branco ao final de cada tempo para index do gnuplot */
        fprintf(arq,"\n\n");

    fclose(arq);
}






double gauss(int x, int y,int tam)
{
    /* curva inicial em forma de sino*/

    double A, xc, yc, gauss, sigmax, sigmay;
    //xc = (tam-1) / 2.;
    //yc = (tam-1) / 2.;
    xc = 0;
    yc = 0;

    A = 1;
    sigmax = 1;
    sigmay = 1;

    gauss = A * exp(-0.5*pow(((x-xc)/sigmax),2) -0.5*pow(((y-yc)/sigmay),2));

    return gauss;
}




/* a funcao H corresponde ao formato do terreno, retorna a profundidade em relação a aguas calmas */

double H(int x, int y,int tam)
{
    /* curva para o formato do terreno em forma de sino virado*/
    double A,xc,yc,h,sigmax,sigmay;
    //xc = (tam-1) / 2.;
    //yc = (tam-1) / 2.;

    A = 1;
    sigmax = 1;
    sigmay = 1;
    xc = 0;
    yc = 0;

    h = 1 - A * exp(-0.5*pow(((x-xc)/sigmax),2) -0.5*pow(((y-yc)/sigmay),2));

    return h;
}

void atualizar_onda(double u_new[][ny_], double u_now[][ny_], double u_old[][ny_], double lambda[][ny_], double a,  double b,  double c, int nx, int ny, double rx, double ry)
{
// DOUBLE U_NEW[][NY_)] SINALIZA PARA O C QUE A FUNÇÃO RECEBERA UMA MATRIZ( TECNICAMENTE RECEBERA O ENDEREÇO NA MEMORIA DA MATRIZ) POR ISSO NÃO É NECESSARIO RETORNAR NENHUM VALOR
// ESTA "TECNICA" É POSSIVEL POIS O NOME DA MATRIZ, NO CASO U_NEW, É NA VERDADE O ENDEREÇO DESSA MATRIZ NA MEMORIA. COMO ESTAMOS PASSANDO O ENDEREÇO NA MEMORIA, A FUNÇÃO CONSEGUE ALTERAR OS VALORES SEM NECESSIDADE DE RETORNO
// PRECISAMOS DECLARAR O [NY_] NA FUNÇÃO POR QUESTÕES TECNICAS. MAS PENSEM NESSA SINTAXE COMO: PASSANDO O ENDEREÇO DA MATRIX PARA A FUNÇÃO, SEM NECESSIDADE DE RETORNO. A FUNÇÃO É LIVRE PARA EDITAR A PROPRIA MATRIZ

    int i,j;

    // LOOP DUPLO PARA ATUALIZAR AS PARTES INTERNAS DA MATRIZ
    for(j = 1 ; j < ny - 1 ; j++)
    {
        for(i = 1 ; i < nx - 1  ; i++)

            // SEPAREI PARTE DA EQUAÇAO EM OUTRA FUNÇÃO PARA SIMPLIFICAR A VIDA. DELTA_U É SIMPLESMENTE UMA PARTE DA EQUAÇÃO ORIGINAL

            u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j-1,j+1);
    }

    //PRECISAMOS AGORA ATUALIZAR AS LINHAS E COLUNAS EXTERNAS DA MATRIZ, POIS ESTAS NÃO FORAM INCLUIDAS NO LOOP ANTERIOR. ESTA AÇÃO NÃO ATUALIZA AS PONTAS, OU QUINAS, DA MATRIZ


    i = 0; // ATUALiZANDO A PRIMEIRA COLUNA DA MATRIZ
    for( j = 1; j < ny - 1  ; j++)
    {
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j-1,j+1);
    }

    i = nx - 1;// ATUALZANDO A ULTIMA COLUNA DA MATRIZ
    for( j = 1; j < ny - 1  ; j++)
    {
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j-1,j+1);
    }

    // ---------------------- //


    j = 0; // ATUALZANDO A PRIMEIRA LINHA DA MATRIZ
    for( i = 1; i < nx - 1 ; i++)
    {
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j+1,j+1);

    }


    j = ny - 1; // ATUALZANDO A ULTIMA LINHA DA MATRIZ
    for( i = 1; i < nx - 1 ; i++)
    {
        u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i+1,j-1,j-1); 

    }


    // AGORA VAMOS ATUALIZAR as PONTAS DA MATRIZ. OU CANTOS, SE PREFERIR CHAMAR ASSIM


    // PONTA [0][0]
    i = 0;
    j = 0;
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j+1,j+1);


    // PONTA [nx - 1][0]
    i= nx - 1;
    j= 0;
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j+1,j+1);


    // PONTA [0][ny -1]
    i= 0;
    j= ny - 1;
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i+1,i+1,j-1,j-1);


    // PONTA [NX-1][ny -1]
    i= nx - 1;
    j= ny - 1;
    u_new[i][j] = a * 2 * u_now[i][j] - b * u_old[i][j] + c * delta_u(rx,ry,lambda,u_now,i,j,i-1,i-1,j-1,j-1);


}

double delta_u( double rx, double ry, double lambda[][ny_],  double u_now[][ny_], int i,  int j, int  im1, int ip1, int jm1, int jp1)
{
    //CALCULAMOS AQUI  SEPARADO UMA PARTE DA EQUAÇÃO, POIS ELA MUDA DEPENDENDO DO QUE ESTAMOS CALCULANDO. SEJA UMA COLUNA INICIAL OU FINAL OU UM CANTO DA MATRIZ
    //PARA ISSO COLOQUEI VALORES AUXILIARES DE IM1, IP1, JM1, JP1 . P DE PLUS E M DE MINUS.POIS ESTES VALORES SAO TROCADOS EM VARIAS PARTES

    return (
               pow(rx,2) * ( ((0.5 * (lambda[ip1][j] + lambda[i][j])) * (u_now[ip1][j] - u_now[i][j]))
                             -  ((0.5 * (lambda[i][j] + lambda[im1][j])) * (u_now[i][j] - u_now[im1][j])))


               + pow(ry,2) * ( ((0.5 * (lambda[i][jp1] + lambda[i][j])) * (u_now[i][jp1] - u_now[i][j]))
                               -  ((0.5 * (lambda[i][j] + lambda[i][jm1])) * (u_now[i][j] - u_now[i][jm1]))));

}

<source>

==Bibliografia==
<references/>


Erro de citação: existem marcas <ref>, mas nenhuma marca <references/> foi encontrada

Disponível em "http://fiscomp.if.ufrgs.br/index.php?title=Grupo2_-_Ondas1&oldid=1183"