Equação de Ginzburg-Landau complexa: mudanças entre as edições
Sem resumo de edição |
|||
| (48 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
A equação de Ginzburg-Landau complexa (CGLE) surgiu inicialmente em 1969 como um modelo para o inicio de instabilidades em problemas de convecção de fluídos. A partir de então, ela se tornou uma das equações não lineares mais estudadas da física, descrevendo uma variedade enorme de fenômenos como: | A equação de Ginzburg-Landau complexa (CGLE) surgiu inicialmente em 1969 como um modelo para o inicio de instabilidades em problemas de convecção de fluídos. A partir de então, ela se tornou uma das equações não lineares mais estudadas da física, descrevendo uma variedade enorme de fenômenos como: | ||
| Linha 8: | Linha 7: | ||
* Superfluidez; | * Superfluidez; | ||
* Condensado de Bose-Einstein. | * Condensado de Bose-Einstein. | ||
A equação de Ginzburg-Landau complexa, quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo: | A equação de Ginzburg-Landau complexa, quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo: | ||
| Linha 16: | Linha 14: | ||
</math> | </math> | ||
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. | |||
== Dedução == | == Dedução == | ||
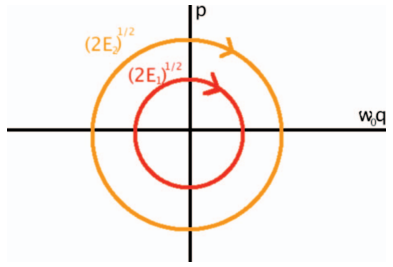
[[File:Phase_space_circle.png|thumb|right|Espaço de fase do oscilador harmônico]] | |||
A energia de um oscilador harmônico é expressa pela equação abaixo, onde <math>E</math> é a energia, <math>q'</math> e <math>p'</math> a coordenada e seu respectivo momento, <math>m</math> é a massa e <math>\omega_0</math> a frequência angular | |||
<math> | |||
E = \frac{p'^2}{2m} + \frac{1}{2} m \omega_0^2 q'^2. | |||
</math> | |||
Ao realizar as seguintes mudanças de variáveis, <math>q'=q/m^{1/2}</math> e <math>p' = p m^{1/2}</math>, a equação da energia produz trajetórias circulares no espaço de fase de <math>\omega_0 q</math> e <math>p</math> | |||
<math> | |||
E = \frac{p^2}{2} + \frac{1}{2}\omega_0^2 q'^2. | |||
</math> | |||
Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde <math>R</math> é a amplitude e <math>\phi</math> a fase | |||
<math> | |||
\dot{R} = 0, \quad \dot{\phi} = \omega_0. | |||
</math> | |||
Definindo a variável complexa <math>A = R e^{i \phi}</math>, a equação acima pode ser reescrita como | |||
<math> | |||
\dot{A} = i \omega_0 A. | |||
</math> | |||
Realizando a transformação de variável <math>A \rightarrow A e^{i \chi}</math>, com <math>\chi \in \mathbb{R}</math>, a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear <math>f(A, A^*)</math> tal que | |||
<math> | |||
\dot{A} = i \omega_0 A + f(A, A^*), | |||
</math> | |||
também seja invariante a rotações. | |||
Então, perante às transformações <math>A \rightarrow A e^{i \chi}</math> e <math>A^* \rightarrow A e^{-i \chi}</math>, a função <math>f(A, A^*)</math> deve satisfazer | |||
<math> | |||
f(A e^{i \chi}, A e^{-i \chi}) = f(A, A^*) e^{i \chi}, | |||
</math> | |||
para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original. | |||
Edição das 15h24min de 27 de abril de 2024
A equação de Ginzburg-Landau complexa (CGLE) surgiu inicialmente em 1969 como um modelo para o inicio de instabilidades em problemas de convecção de fluídos. A partir de então, ela se tornou uma das equações não lineares mais estudadas da física, descrevendo uma variedade enorme de fenômenos como:
- Ondas não lineares;
- Transições de fase de segunda ordem;
- Supercondutividade;
- Superfluidez;
- Condensado de Bose-Einstein.
A equação de Ginzburg-Landau complexa, quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço.
Dedução
A energia de um oscilador harmônico é expressa pela equação abaixo, onde é a energia, e a coordenada e seu respectivo momento, é a massa e a frequência angular
Ao realizar as seguintes mudanças de variáveis, e , a equação da energia produz trajetórias circulares no espaço de fase de e
Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde é a amplitude e a fase
Definindo a variável complexa , a equação acima pode ser reescrita como
Realizando a transformação de variável , com , a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear tal que
também seja invariante a rotações.
Então, perante às transformações e , a função deve satisfazer
para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original.