Equação de Ginzburg-Landau complexa: mudanças entre as edições
| (144 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
A equação de Ginzburg-Landau complexa (CGLE) é uma das equações não lineares mais estudadas da física. Ela oferece uma descrição geral de sistemas com uma fraca dependência não linear. Quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo: | |||
= | <math> | ||
\frac{\partial A}{\partial t} = (1+ib)\nabla^2 A + A - (1+ic) A|A|^2. | |||
</math> | |||
Em especial, para <math>b = 0</math> e <math>c = 0</math>, ela se reduz para a equação de Ginzburg-Landau real. E, para <math>b \rightarrow + \infty </math> e <math>c \rightarrow + \infty</math>, ela se reduz à equação de Schrödinger não linear. Ela descreve uma variedade enorme de fenômenos, como: | |||
:<math>\frac{\partial A}{\partial t} = (1+ | * Ondas não lineares; | ||
* Transições de fase de segunda ordem; | |||
* Supercondutividade; | |||
* Superfluidez; | |||
* Condensado de Bose-Einstein. | |||
== Dedução == | |||
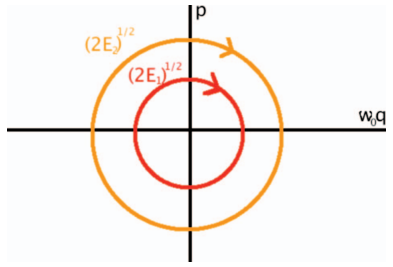
[[File:Phase_space_circle.png|thumb|right|Figura 1 - Espaço de fase do oscilador harmônico. Fonte - Cross, M., & Greenside, H. (2009)]] | |||
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. A energia de um oscilador harmônico é expressa pela equação abaixo, onde <math>E</math> é a energia, <math>q</math> e <math>p</math> a coordenada e seu respectivo momento, <math>m</math> é a massa e <math>\omega_0</math> a frequência angular | |||
<math> | |||
E = \frac{p^2}{2m} + \frac{1}{2} m \omega_0^2 q^2. | |||
</math> | |||
Ao realizar as seguintes mudanças de variáveis, <math>q \rightarrow q/m^{1/2}</math> e <math>p \rightarrow p m^{1/2}</math>, a equação da energia produz trajetórias circulares no espaço de fase de <math>\omega_0 q</math> e <math>p</math> | |||
<math> | |||
E = \frac{p^2}{2} + \frac{1}{2}\omega_0^2 q^2. | |||
</math> | |||
Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde <math>R</math> é a amplitude e <math>\phi</math> a fase | |||
<math> | |||
\dot{R} = 0, \quad \dot{\phi} = \omega_0. | |||
</math> | |||
Define-se, então, a variável complexa <math>A = R e^{i \phi}</math>, portanto a equação acima pode ser reescrita como | |||
<math> | |||
\dot{A} = i \omega_0 A. | |||
</math> | |||
Ao realizar a transformação de variável <math>A \rightarrow A e^{i \chi}</math>, com <math>\chi \in \mathbb{R}</math>, a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear <math>f(A, A^*)</math> tal que | |||
<math> | |||
\dot{A} = i \omega_0 A + f(A, A^*) | |||
</math> | |||
também seja invariante a rotações. | |||
Então, perante às transformações <math>A \rightarrow A e^{i \chi}</math> e <math>A^* \rightarrow A^* e^{-i \chi}</math>, a função <math>f(A, A^*)</math> deve satisfazer | |||
<math> | |||
f(A e^{i \chi}, A^* e^{-i \chi}) = f(A, A^*) e^{i \chi}, | |||
</math> | |||
para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original. | |||
Considerando pequenas oscilações, é possível expandir <math>f(A, A^*)</math> em potências de <math>A</math> e <math>A^*</math> até a menor ordem possível que satisfaça a condição e que introduza uma não linearidade à equação. Com isso, obtém-se | |||
<math> | |||
f(A, A^*) = \alpha_1 A + \alpha_2 |A|^2 A, \quad \alpha_1 = \alpha_{1r} + i \alpha_{1i}, \quad \alpha_2 = \alpha_{2r} + i \alpha_{2i} | |||
</math> | |||
Utilizando o resultado encontrado e expressando em coordenadas polares por meio de <math>A = R e^{i\phi}</math> | |||
<math> | |||
\dot{R} = \alpha_{1r} R + \alpha_{2r} R^3, \quad \dot{\phi} = \omega_0 + \alpha_{1i} + \alpha_{2i} R^2. | |||
</math> | |||
Em seguida, muda-se para o referencial que gira com a mesma frequência do oscilador harmônico por meio da definição de <math>\phi = \varphi + \omega_0 t</math>. As novas equações obtidas são | |||
<math> | |||
\dot{R} = \alpha_{1r} R + \alpha_{2r} R^3, \quad \dot{\varphi} = \alpha_{1i} + \alpha_{2i} R^2. | |||
</math> | |||
Para encontrar a amplitude estacionária, pode-se tomar <math>\dot{R} = 0</math> na equação, o que resulta na solução trivial <math>R^{(est)} = 0</math> e <math>R^{(est)} = \sqrt{-\alpha_{1r}/\alpha_{2r}}</math>. Então, para que exista uma amplitude estacionária não nula, os sinais de <math>\alpha_{1r}</math> e de <math>\alpha_{2r}</math> devem ser opostos. Além disso, por inspeção observa-se que, caso <math>\alpha_{1r} < 0</math> e <math>\alpha_{2r} > 0</math>, pequenos valores de amplitude irão diminuir e grandes valores de amplitude irão aumentar, o que indica que a solução estacionária não trivial será instável. Portanto, define-se <math>\alpha_{1r} = \mu \sigma_1</math> para <math>\sigma_1 > 0</math>, <math>\alpha_{2i} = \mu \omega_1</math>, <math>\alpha_{2r} = -g_r</math> com <math>g_r > 0</math> e <math>\alpha_{2i} = - g_i</math>. Por fim, ao voltar para a representação no plano complexo, chega-se em | |||
<math> | |||
\dot{A} = \mu (\sigma_1 + \omega_1) A - (g_r + ig_i)|A|^2 A | |||
</math> | |||
Esta é a equação de Stuart-Landau. Para obter a equação complexa de Ginzburg-Landau, é necessário considerar um sistema espacialmente extenso, em que cada ponto é um oscilador modelado pela equação acima. Para isso, é adicionado um termo proporcional ao laplaciano de A, <math>(d_r + i d_i)\nabla^2 A</math>, cujo significado fica evidente ao discretizar a função. Ele computa a diferença de <math>A</math> no sítio em questão com relação à média dos sítios vizinhos, resultando em uma tendência de pontos próximos oscilarem com amplitudes e fases semelhantes. Ao adicionar esse novo termo e redefinir as constantes de modo a reduzi-las sem perder as características importantes do sistema, chega-se na equação complexa de Ginzburg-Landau | |||
<math> | |||
\frac{\partial A}{\partial t} = (1+ib)\nabla^2 A + A - (1+ic) A|A|^2. | |||
</math> | |||
== Método FTCS == | |||
Para estudar o comportamento das soluções foi utilizados o método FTCS(Foward-Time Central-Space) explícito que consiste em discretizar o domínio temporal e o espacial da equação, resolvemos as derivadas espaciais por uma aproximação dos pontos vizinhos ao ponto que queremos encontrar, enquanto atualizamos a parte temporal, também por uma aproximação como na parte espacial, porém fazemos por diferenciação entre a taxa de variação (solução futura) e a solução atual. | |||
A partir da CGLE em duas dimensões: | |||
<math> | |||
\frac{\partial A}{\partial t} = \alpha(\frac{\partial^2 A}{\partial x^2}+\frac{\partial^2 A}{\partial y^2}) + A - \beta A|A|^2. | |||
</math> | |||
para | |||
<math> | |||
\alpha = (1+ib); \beta = (1+ic) | |||
</math> | |||
Aplicamos o método da seguinte maneira: | |||
<math> | |||
\frac{A(x,y,t+\Delta t) - A(x,y,t)}{\Delta t} = \alpha(\frac{A(x+\Delta x,y,t) - 2*A(x,y,t) + A(x-\Delta x,y,t)}{\Delta x^2}+\frac{A(x,y+\Delta y,t) - 2*A(x,y,t) + A(x,y-\Delta y,t)}{\Delta y^2}) + A(x,y,t) - \beta A(x,y,t)|A(x,y,t)|^2. | |||
</math> | |||
<math> | |||
\frac{A_{i,j}^{N+1} - A_{i,j}^{N}}{\Delta t} = \alpha(\frac{A_{i+1,j}^{N} - 2*A_{i,j}^{N} + A_{i-1,j}^{N}}{\Delta x^2}+\frac{A_{i,j+1}^{N} - 2*A_{i,j}^{N} + A_{i,j-1}^{N}}{\Delta y^2}) + A_{i,j}^{N} - \beta A_{i,j}^{N}|A_{i,j}^{N}|^2. | |||
</math> | |||
Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y (<math>\Delta y = \Delta x</math>), chegamos em : | |||
<math> | |||
A_{i,j}^{N+1} = A_{i,j}(1+\Delta t(1-\beta|A_{i,j}|^2))+\frac{\Delta t \alpha}{\Delta x^2}(A_{i+1,j}+A_{i-1,j}+A_{i,j+1}+A_{i,j-1} - 4*A_{i,j}) | |||
</math> | |||
[[File:newplot.png|thumb|120px|right|Figura 2 - Condições de contorno periódicas em duas dimensões.]] | |||
Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando | |||
i=L+1 estaremos em i=1. | |||
e para y, da mesma forma, | |||
j=L+1 temos que j=1. | |||
A figura 2 é a representação gráfica dessas condições. | |||
== Soluções == | |||
[[File:diagrama_de_fase.png|thumb|240px|upright|Figura 3 - Diagrama de fase para soluções da CGLE [3].]] | |||
A partir da variação dos parâmetros <math>b</math> e <math>c</math> temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia central foi começar com condição inicial de onda plana, que em teoria tende a se manter como onda plana, e perturbar essa solução, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo as principais: | |||
*Soluções de onda plana estável | |||
*Soluções de onda plana instável | |||
que são delimitadas pela condição de Benjamin-Feir-Newell, que descreve a linha BFN no diagrama de fase, a condição para instabilidade é descrita por <math>1 + bc < 0</math>, ou seja, acima da linha temos soluções estáveis e abaixo soluções instáveis. | |||
Outras soluções que podem ser encontradas são soluções de turbulência, para fase e para a amplitude, | |||
condição tipos de espirais <math>-(c3 + c1)/(1 -c1*c3) = 0.845</math> Linha OR, interação entre espirais. | |||
esquerda de T dinâmico turbulento, direita "congelado". | |||
L limite da turbulência de fase | |||
Eckhaus-stability boundary EI | |||
boundary of | |||
absolute stability AI | |||
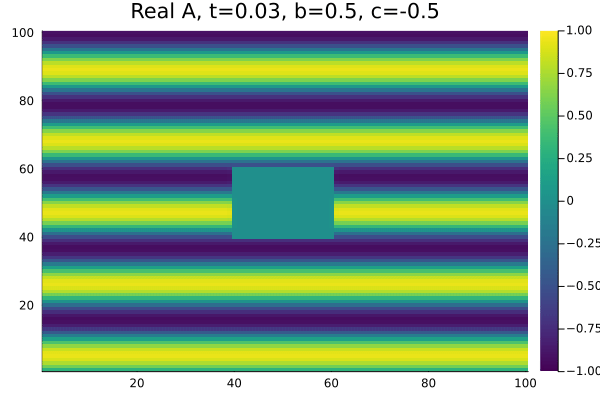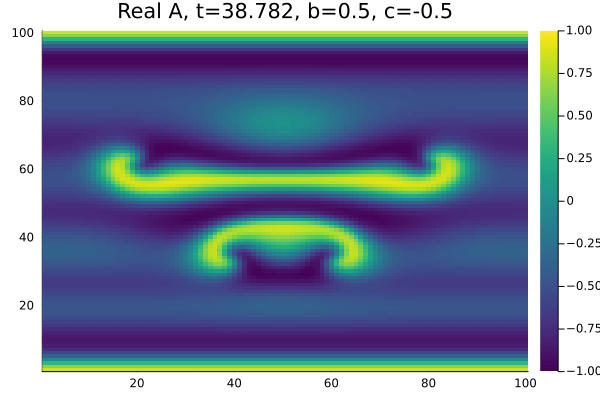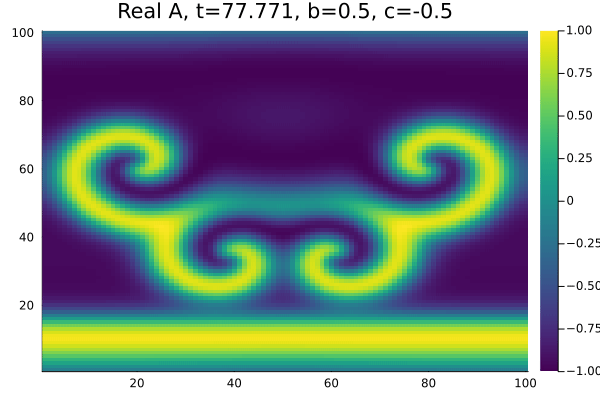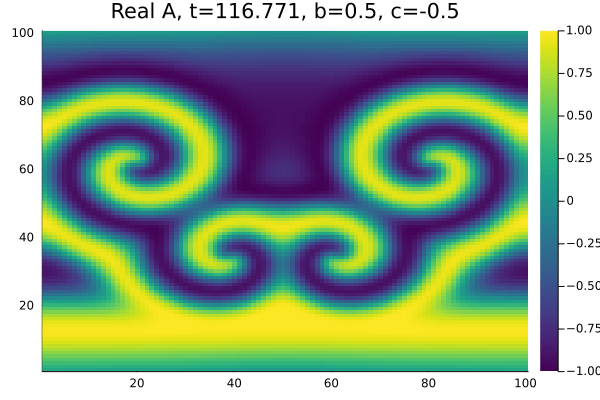
Quando definimos as condições iniciais de onda plana como um seno e um termo perturbando as oscilações em <math>x=[40,60]</math>, <math>y=[40,60]</math> | |||
com <math>b=0.5</math>, <math>c=-0.5</math> do diagrama de fase em (figura 3) o sistema apresenta simetria entre as espirais no gráfico da parte real e também | |||
percebemos a presença de defeitos no módulo de <math>A(\chi,t)</math> (figura 4). Os defeitos, caracterizados pela presença de um ponto nulo no módulo | |||
da amplitude, nao se anularam pois os parametros <math>b</math> e <math>c</math> encontram-se em uma região de instabilidade convectiva (formação de espirais bem definidas). | |||
[[File:LiquidoVortices.gif|400px|Figura 4 -.Liquidos de Vortices]][[File:LiquidoVorticesAbs.gif|400px|Figura 5 -.Modulo para Liquidos de Vortices]] | |||
Partindo das mesmas condições iniciais anteriores porém em uma região onde <math>b=-2.5</math>, <math>c=-0.1</math>, denominada Vidro de Vórtices, o padrão de | |||
espirais muda, a simetria é perdida e algumas apresentam comportamento "dominante?". Outra característica é a presença de maior número de | |||
células de defeitos que são "empurradas" pelas células maiores provenientes das grandes espirais. É interessante ressaltar que os pontos defeitos se anulam | |||
somente aos pares. | |||
[[File:VidroVortices.gif|400px|Figura 6 -.Vidro de Vortices]][[File:VidroVorticesAbs.gif|400px|Figura 7 -.Modulo para Vidro de Vortices]] | |||
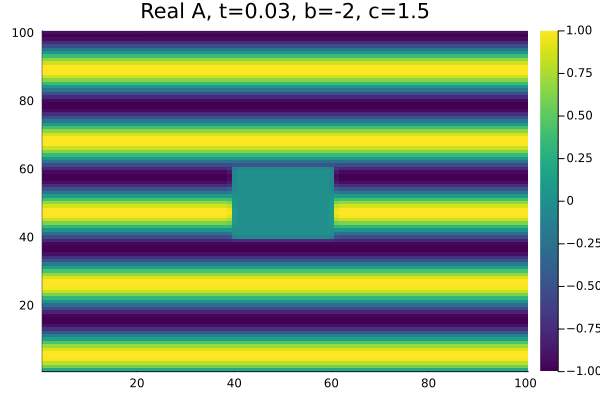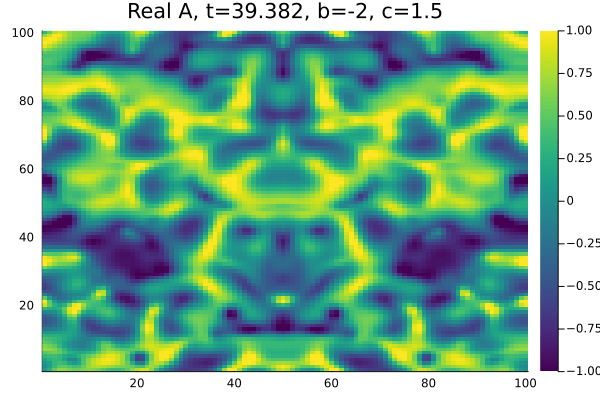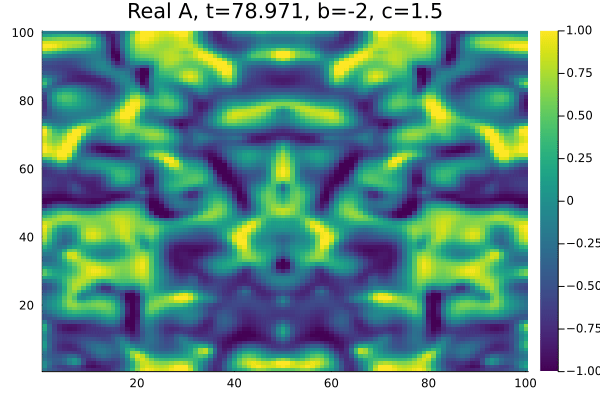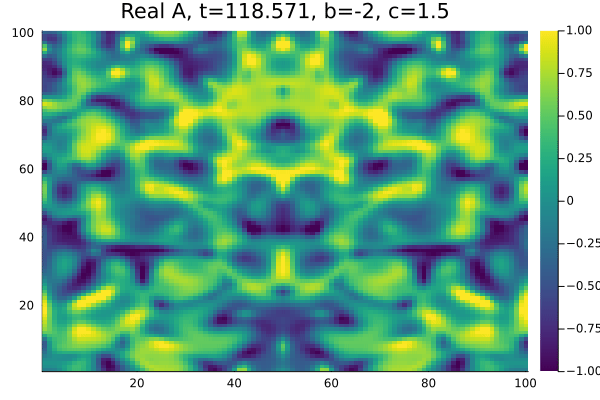
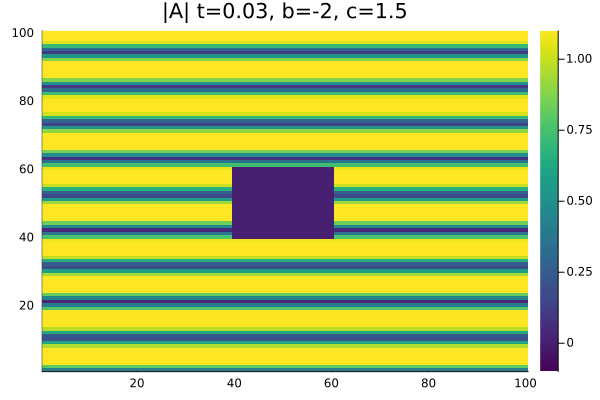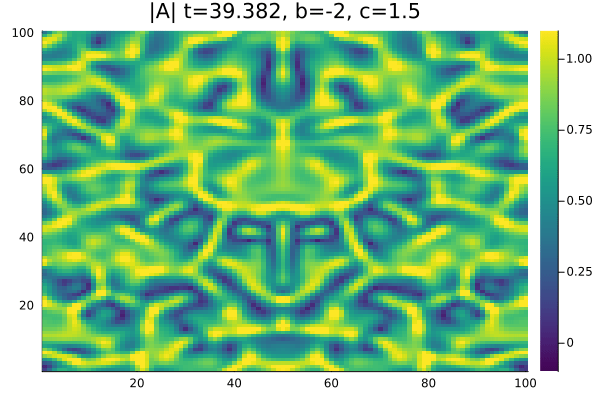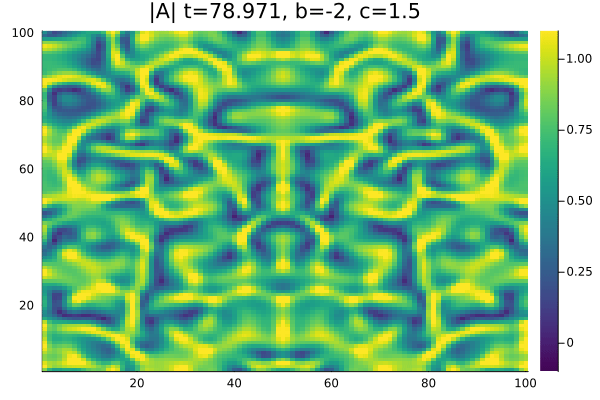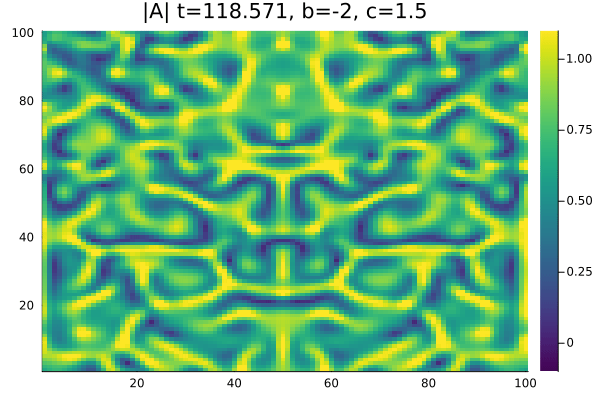
Por fim, na região chamada de Turbulência de Amplitude <math>b=-2</math>, <math>c=1.5</math> à direita da linha AI nao encontramos espirais, as células de | |||
defeitos não se formam e temos apenas um comportamento caótico no módulo e na fase da Amplitude. | |||
[[File:TurbAmplitude.gif|400px|Figura 8 -.Turbulencia de Amplitude]][[File:TurbAmplitudeAbs.gif|400px|Figura 9 -.Modulo para Turbulencia de Amplitude]] | |||
== Referências == | |||
[1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554 | |||
[2] H. Riecke, (2021). Methods of Nonlinear Analysis | |||
[3] Igor S. Aranson, Lorenz Kramer, (2001). The World of the Complex Ginzburg-Landau Equation | |||
[4] Cross, M., & Greenside, H. (2009). Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press. | |||
[5] Hugues Chaté, Paul Manneville (1996). Phase diagram of the two-dimensional complex Ginzburg-Landau equation. Physica A: Statistical Mechanics and its Applications | |||
Edição atual tal como às 09h53min de 8 de maio de 2024
A equação de Ginzburg-Landau complexa (CGLE) é uma das equações não lineares mais estudadas da física. Ela oferece uma descrição geral de sistemas com uma fraca dependência não linear. Quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:
Em especial, para e , ela se reduz para a equação de Ginzburg-Landau real. E, para e , ela se reduz à equação de Schrödinger não linear. Ela descreve uma variedade enorme de fenômenos, como:
- Ondas não lineares;
- Transições de fase de segunda ordem;
- Supercondutividade;
- Superfluidez;
- Condensado de Bose-Einstein.
Dedução
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. A energia de um oscilador harmônico é expressa pela equação abaixo, onde é a energia, e a coordenada e seu respectivo momento, é a massa e a frequência angular
Ao realizar as seguintes mudanças de variáveis, e , a equação da energia produz trajetórias circulares no espaço de fase de e
Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde é a amplitude e a fase
Define-se, então, a variável complexa , portanto a equação acima pode ser reescrita como
Ao realizar a transformação de variável , com , a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear tal que
também seja invariante a rotações.
Então, perante às transformações e , a função deve satisfazer
para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original.
Considerando pequenas oscilações, é possível expandir em potências de e até a menor ordem possível que satisfaça a condição e que introduza uma não linearidade à equação. Com isso, obtém-se
Utilizando o resultado encontrado e expressando em coordenadas polares por meio de
Em seguida, muda-se para o referencial que gira com a mesma frequência do oscilador harmônico por meio da definição de . As novas equações obtidas são
Para encontrar a amplitude estacionária, pode-se tomar na equação, o que resulta na solução trivial e . Então, para que exista uma amplitude estacionária não nula, os sinais de e de devem ser opostos. Além disso, por inspeção observa-se que, caso e , pequenos valores de amplitude irão diminuir e grandes valores de amplitude irão aumentar, o que indica que a solução estacionária não trivial será instável. Portanto, define-se para , , com e . Por fim, ao voltar para a representação no plano complexo, chega-se em
Esta é a equação de Stuart-Landau. Para obter a equação complexa de Ginzburg-Landau, é necessário considerar um sistema espacialmente extenso, em que cada ponto é um oscilador modelado pela equação acima. Para isso, é adicionado um termo proporcional ao laplaciano de A, , cujo significado fica evidente ao discretizar a função. Ele computa a diferença de no sítio em questão com relação à média dos sítios vizinhos, resultando em uma tendência de pontos próximos oscilarem com amplitudes e fases semelhantes. Ao adicionar esse novo termo e redefinir as constantes de modo a reduzi-las sem perder as características importantes do sistema, chega-se na equação complexa de Ginzburg-Landau
Método FTCS
Para estudar o comportamento das soluções foi utilizados o método FTCS(Foward-Time Central-Space) explícito que consiste em discretizar o domínio temporal e o espacial da equação, resolvemos as derivadas espaciais por uma aproximação dos pontos vizinhos ao ponto que queremos encontrar, enquanto atualizamos a parte temporal, também por uma aproximação como na parte espacial, porém fazemos por diferenciação entre a taxa de variação (solução futura) e a solução atual. A partir da CGLE em duas dimensões:
para
Aplicamos o método da seguinte maneira:
Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y (), chegamos em :
Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando
i=L+1 estaremos em i=1.
e para y, da mesma forma,
j=L+1 temos que j=1.
A figura 2 é a representação gráfica dessas condições.
Soluções
A partir da variação dos parâmetros e temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia central foi começar com condição inicial de onda plana, que em teoria tende a se manter como onda plana, e perturbar essa solução, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo as principais:
- Soluções de onda plana estável
- Soluções de onda plana instável
que são delimitadas pela condição de Benjamin-Feir-Newell, que descreve a linha BFN no diagrama de fase, a condição para instabilidade é descrita por , ou seja, acima da linha temos soluções estáveis e abaixo soluções instáveis. Outras soluções que podem ser encontradas são soluções de turbulência, para fase e para a amplitude,
condição tipos de espirais Linha OR, interação entre espirais.
esquerda de T dinâmico turbulento, direita "congelado".
L limite da turbulência de fase
Eckhaus-stability boundary EI
boundary of absolute stability AI
Quando definimos as condições iniciais de onda plana como um seno e um termo perturbando as oscilações em , com , do diagrama de fase em (figura 3) o sistema apresenta simetria entre as espirais no gráfico da parte real e também percebemos a presença de defeitos no módulo de (figura 4). Os defeitos, caracterizados pela presença de um ponto nulo no módulo da amplitude, nao se anularam pois os parametros e encontram-se em uma região de instabilidade convectiva (formação de espirais bem definidas).
Partindo das mesmas condições iniciais anteriores porém em uma região onde , , denominada Vidro de Vórtices, o padrão de espirais muda, a simetria é perdida e algumas apresentam comportamento "dominante?". Outra característica é a presença de maior número de células de defeitos que são "empurradas" pelas células maiores provenientes das grandes espirais. É interessante ressaltar que os pontos defeitos se anulam somente aos pares.
Por fim, na região chamada de Turbulência de Amplitude , à direita da linha AI nao encontramos espirais, as células de defeitos não se formam e temos apenas um comportamento caótico no módulo e na fase da Amplitude.
Referências
[1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554
[2] H. Riecke, (2021). Methods of Nonlinear Analysis
[3] Igor S. Aranson, Lorenz Kramer, (2001). The World of the Complex Ginzburg-Landau Equation
[4] Cross, M., & Greenside, H. (2009). Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.
[5] Hugues Chaté, Paul Manneville (1996). Phase diagram of the two-dimensional complex Ginzburg-Landau equation. Physica A: Statistical Mechanics and its Applications



























































![{\displaystyle x=[40,60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de037a52a0c4c2716f67f498504471c0e87ad342)
![{\displaystyle y=[40,60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94223a112efec22caf92562cc6b960f4937555b2)