Equação de Dirac: mudanças entre as edições
(→Introdução: explicação de spinor) |
|||
| (49 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 36: | Linha 36: | ||
as componentes de <math>\Psi</math> representam as funções de onda associadas ao elétron e ao pósitron: <math>\Phi_1</math> (<math>\Phi_2</math>) representa a função de onda do elétron com spin up (down), e <math>\Phi_3</math> (<math>\Phi_4</math>) representa a função de onda do pósitron com spin up (down). O objeto <math>\Psi(\boldsymbol{x},t)</math> é chamado de ''spinor''. | as componentes de <math>\Psi</math> representam as funções de onda associadas ao elétron e ao pósitron: <math>\Phi_1</math> (<math>\Phi_2</math>) representa a função de onda do elétron com spin up (down), e <math>\Phi_3</math> (<math>\Phi_4</math>) representa a função de onda do pósitron com spin up (down). O objeto <math>\Psi(\boldsymbol{x},t)</math> é chamado de ''spinor''. | ||
=Dedução da equação de Dirac em duas dimensões= | =Dedução da equação de Dirac em uma e duas dimensões= | ||
Consideraremos neste trabalho a equação de Dirac em duas dimensões, <math>x</math> e <math>y</math>. A escolha dessas coordenadas se dá pela conveniência do acoplamento das EDPs: nesse caso, as quatro equações acopladas passam a ser acopladas duas a duas, facilitando o estudo do sistema. | Consideraremos neste trabalho a equação de Dirac em uma e duas dimensões, <math>x</math> e <math>y</math>. A escolha dessas coordenadas se dá pela conveniência do acoplamento das EDPs: nesse caso, as quatro equações acopladas passam a ser acopladas duas a duas, facilitando o estudo do sistema. A dedução aqui apresentada é baseada em [[Equação_de_Dirac#Referências|(1)]] e [[Equação_de_Dirac#Referências|(2)]]. | ||
==Construção do Hamiltoniano completo== | ==Construção do Hamiltoniano completo== | ||
| Linha 129: | Linha 129: | ||
</math> | </math> | ||
</center> | </center> | ||
Novamente utilizando a notação matricial, obtemos | |||
<center> | |||
<math> | |||
\begin{pmatrix} | |||
i \frac{\partial}{\partial t} - V - V_{sc} - 1 & 0 & 0 & i \frac{\partial}{\partial x} + \frac{\partial}{\partial y} \\ | |||
0 & i \frac{\partial}{\partial t} - V - V_{sc} - 1 & i \frac{\partial}{\partial x} - \frac{\partial}{\partial y} & 0 \\ | |||
0 & i \frac{\partial}{\partial x} + \frac{\partial}{\partial y} & i \frac{\partial}{\partial t} - V + V_{sc} + 1 & 0 \\ | |||
i \frac{\partial}{\partial x} - \frac{\partial}{\partial y} & 0 & 0 & i \frac{\partial}{\partial t} - V + V_{sc} + 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} \Phi_1 \\ \Phi_2 \\ \Phi_3 \\ \Phi_4 \end{pmatrix} | |||
= 0 | |||
</math> | |||
</center> | |||
Realizando a multiplicação matricial, pode-se ver que se obtém dois sistemas acoplados: <math>\Phi_1</math> com <math>\Phi_4</math> e <math>\Phi_2</math> com <math>\Phi_3</math>. Escolhendo o sistema de <math>\Phi_1</math> com <math>\Phi_4</math>: | |||
<center> | |||
<math> | |||
\begin{cases} | |||
\left(i \dfrac{\partial}{\partial t} - V - V_{sc} - 1\right) \Phi_1 + \left(i \dfrac{\partial}{\partial x} + \dfrac{\partial}{\partial y}\right) \Phi_4 = 0 \\ | |||
\left(i \dfrac{\partial}{\partial x} - \dfrac{\partial}{\partial y}\right) \Phi_1 + \left(i \dfrac{\partial}{\partial t} - V + V_{sc} + 1\right) \Phi_4 = 0 | |||
\end{cases} | |||
</math> | |||
</center> | |||
Simplificando e isolando a derivada temporal, obtemos por fim | |||
<center> | |||
<math> | |||
\begin{cases} | |||
\dfrac{\partial \Phi_1}{\partial t} = -i(V + V_{sc} + 1) \Phi_1 -\dfrac{\partial \Phi_4}{\partial x} + i\dfrac{\partial \Phi_4}{\partial y} \\ | |||
\dfrac{\partial \Phi_4}{\partial t} = -i(V - V_{sc} - 1) \Phi_4 -\dfrac{\partial \Phi_1}{\partial x} - i\dfrac{\partial \Phi_1}{\partial y} | |||
\end{cases} | |||
</math> | |||
</center> | |||
Por fim, a equação em uma dimensão (<math>x</math>) é facilmente obtida: basta fazer <math>\dfrac{\partial \Phi_1}{\partial y} = \dfrac{\partial \Phi_4}{\partial y} = 0</math> | |||
<center> | |||
<math> | |||
\begin{cases} | |||
\dfrac{\partial \Phi_1}{\partial t} = -i(V + V_{sc} + 1) \Phi_1 -\dfrac{\partial \Phi_4}{\partial x} \\ | |||
\dfrac{\partial \Phi_4}{\partial t} = -i(V - V_{sc} - 1) \Phi_4 -\dfrac{\partial \Phi_1}{\partial x} | |||
\end{cases} | |||
</math> | |||
</center> | |||
Neste trabalho, serão considerados principalmente problemas apenas com o potencial <math>V</math>; assim, caso indicado o contrário, será assumido <math>V_{sc}=0</math>. | |||
=Discretização= | =Discretização= | ||
A equação de Dirac 1D pode ser escrita, na forma matricial, como | |||
<center> | |||
<math> | |||
i \partial_t \mathbf{\Phi} = [-i\sigma_1\partial_x + \sigma_3] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} | |||
</math> | |||
</center> | |||
onde <math>\mathbf{\Phi} = (\phi_1, \phi_4)^T</math> e <math>I_2</math> é matriz identidade de dimensão 2. As matrizes de Pauli <math>\vec{\sigma}</math> são escritas, aqui, como <math>\sigma_1 = \sigma_x</math> e <math>\sigma_3 = \sigma_z</math>. | |||
Para discretizar uma equação diferencial parcial como essa, é necessário discretizar o espaço e o tempo. Convenciona-se <math>\Delta t</math> como um passo finito de tempo e <math>h</math> como um passo finito no espaço, de tal forma que <math>x_j = x_0 + jh, t_n = t_0 + n\Delta t</math>, onde <math>j,n</math> são números inteiros. Define-se a notação <math>\mathbf{\Phi}(t_n, x_j) = \mathbf{\Phi}_j ^n</math> e também <math>V(t_n,x_n) = V^n _j</math>. Discretiza-se as derivadas parciais explicitamente com uma expansão em série de taylor da própria função: | |||
<center> | |||
<math> | |||
\mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \partial_t \mathbf{\Phi^n _j} \Delta t + \mathcal{O}(\Delta t ^2) | |||
</math> | |||
</center> | |||
Considerando uma derivada discretizada <math>\delta_t \approx \partial_t</math> e truncando na primeira ordem: | |||
<center> | |||
<math> | |||
\delta_t\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} | |||
</math> | |||
</center> | |||
O processo é completamente análogo para a derivada espacial, porém para facilitar a aplicação do método mantém-se o espaço centrado em <math>x_j</math>, em outras palavras faz-se uma expansão em torno de <math>x_{j-1}</math>, obtendo: | |||
<center> | |||
<math> | |||
\delta_x\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^n _{j+1}} - \mathbf{\Phi^n _{j-1}}}{2h} | |||
</math> | |||
</center> | |||
Com isso, obtém-se uma equação para um método explícito no tempo da equação de Dirac 1D. | |||
<center> | |||
<math> | |||
i \delta_t \mathbf{\Phi^n _j} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + [V^n _jI_2] \mathbf{\Phi^n _j} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
i \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + [V^n _jI_2] \mathbf{\Phi^n _j} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
i \mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \Delta t[-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + \Delta t[V^n _jI_2] \mathbf{\Phi^n _j} | |||
</math> | |||
</center> | |||
Pode-se também desenvolver um método implícito no tempo fazendo a expansão de <math>\mathbf{\Phi^{n-1} _j}</math> em torno de <math>t_n</math>, obtendo: | |||
<center> | |||
<math> | |||
\delta_t\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^{n} _j} - \mathbf{\Phi^{n-1} _j}}{\Delta t} | |||
</math> | |||
</center> | |||
Ao aplicar esta aproximação na equação discretizada basta dar um passo a frente em todos os elementos, obtendo um método implícito no tempo, já que há dependência com <math>t_{n+1}</math>. | |||
<center> | |||
<math> | |||
i \mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \Delta t[-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^{n+1} _j} + \Delta t[V^{n+1} _jI_2] \mathbf{\Phi^{n+1} _j} | |||
</math> | |||
</center> | |||
Neste trabalho, foram utilizados dois métodos de integração numérica diferentes: o de Crank-Nicolson, para a equação de Dirac em uma dimensão, e o de Leap-Frog, para a equação em duas dimensões. Deixamos [[Equação_de_Dirac#Referências|(3)]] como referência para estes e outros métodos numéricos aplicados ao problema. | |||
==Método de Crank-Nicolson== | |||
O método de Crank-Nicolson (CN) consiste em uma média entre um método explícito e outro implícito no espaço. Utilizar-se-á a notação <math>\mathbf{\Phi^{n+1/2} _j}</math> para representar justamente a média entre ambos os métodos, ou seja: | |||
<center> | |||
<math> | |||
\mathbf{\Phi^{n+1/2} _j} = \frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2} | |||
</math> | |||
</center> | |||
Define-se a notação: | |||
<center> | |||
<math> | |||
V^{n+1/2} _j\mathbf{\Phi^{n+1/2} _j} = \frac{ V^{n+1} _j\mathbf{\Phi^{n+1} _j} + V^{n} _j\mathbf{\Phi^n _j}}{2} | |||
</math> | |||
</center> | |||
Dessa maneira, enuncia-se o método CN para a equação de Dirac 1D como: | |||
<center> | |||
<math> | |||
i \delta_t \mathbf{\Phi^n _j} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^{n+1/2} _j} + [V^{n+1/2} _jI_2] \mathbf{\Phi^{n+1/2} _j} | |||
</math>, | |||
</center> | |||
onde <math>\delta_t, \delta_x </math> são as discretizações explícitas das derivadas. | |||
Para que seja possível aplicar e estudar o método, é necessário passar da notação matricial para escalar: | |||
<center> | |||
<math> | |||
i \delta_t \mathbf{\Phi^n _j} = -i\sigma_1\delta_x\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + \sigma_3\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + I_2 \left(\frac{V^{n+1} _j \mathbf{\Phi^{n+1} _j} + V^n _j\mathbf{\Phi^n _j}}{2}\right) | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
i \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} = -\frac{i}{2}\sigma_1\left[\frac{\mathbf{\Phi^{n+1} _{j+1}} - \mathbf{\Phi^{n+1} _{j-1}}}{2h} + \frac{\mathbf{\Phi^n _{j+1}} - \mathbf{\Phi^n _{j-1}}}{2h} \right] + \sigma_3\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + I_2 \left(\frac{V^{n+1} _j \mathbf{\Phi^{n+1} _j} + V^n _j\mathbf{\Phi^n _j}}{2}\right) | |||
</math> | |||
</center> | |||
Isolando cada tempo em um lado da igualdade: | |||
<center> | |||
<math> | |||
\left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{\Phi^{n+1} _j} + \frac{\Delta t}{4h}\sigma_1\left[\mathbf{\Phi^{n+1} _{j+1}} - \mathbf{\Phi^{n+1} _{j-1}}\right] = </math> | |||
<math> | |||
\left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _j I_2\right]\mathbf{\Phi^{n} _j} - \frac{\Delta t}{4h}\sigma_1\left[\mathbf{\Phi^{n} _{j+1}} - \mathbf{\Phi^{n} _{j-1}}\right] | |||
</math> | |||
</center> | |||
Abrindo as matrizes <math>\sigma_1, \sigma_3</math> e <math>I_2</math> e operando-as sobre o vetor <math>\mathbf{\Phi}</math> na equação, tem-se: | |||
<center> | |||
<math> | |||
\left(\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & 1 \\ | |||
\end{bmatrix} | |||
+\frac{i\Delta t}{2} | |||
\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & -1 \\ | |||
\end{bmatrix} | |||
+ \frac{i}{2}\Delta t V^{n+1} _j | |||
\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & 1 \\ | |||
\end{bmatrix}\right) | |||
\begin{bmatrix} | |||
\psi^{n+1} _{1,j} \\ | |||
\psi^{n+1} _{4,j} \\ | |||
\end{bmatrix} | |||
+\frac{\Delta t}{4h} | |||
\begin{bmatrix} | |||
0 & 1 \\ | |||
1 & 0 \\ | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
\psi^{n+1} _{1,j+1} - \psi^{n+1} _{1,j-1} \\ | |||
\psi^{n+1} _{4,j+1} - \psi^{n+1} _{4,j-1} \\ | |||
\end{bmatrix} = | |||
\left(\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & 1 \\ | |||
\end{bmatrix} | |||
-\frac{i\Delta t}{2} | |||
\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & -1 \\ | |||
\end{bmatrix} | |||
-\frac{i}{2}\Delta t V^{n} _j | |||
\begin{bmatrix} | |||
1 & 0 \\ | |||
0 & 1 \\ | |||
\end{bmatrix}\right) | |||
\begin{bmatrix} | |||
\psi^{n} _{1,j} \\ | |||
\psi^{n} _{4,j} \\ | |||
\end{bmatrix} | |||
-\frac{\Delta t}{4h} | |||
\begin{bmatrix} | |||
0 & 1 \\ | |||
1 & 0 \\ | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
\psi^{n} _{1,j+1} - \psi^{n} _{1,j-1} \\ | |||
\psi^{n} _{4,j+1} - \psi^{n} _{4,j-1} \\ | |||
\end{bmatrix} | |||
</math> | |||
</center> | |||
Pode-se realizar as operações matriciais e escrever duas equações escalares. Para facilitar a notação, utiliza-se <math>f^n _j = \psi^n _{1,j}</math> e <math>g^n _j = \psi^n _{4,j}</math>: | |||
<center> | |||
<math> | |||
\begin{cases} | |||
\left[1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)\right]f^{n+1} _j + \frac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j + 1)\right]f^{n} _j - \frac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1}) \\ | |||
\left[1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)\right]g^{n+1} _j + \frac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j - 1)\right]g^{n} _j - \frac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) | |||
\end{cases} | |||
</math> | |||
</center> | |||
Tem-se então um número <math>n</math> de equações onde <math>n</math> é o número de elementos do espaço discretizado. Portanto o primeiro termo das duas equações gera uma matriz diagonal, pois multiplica os termos espaciais dependentes de <math>x_j</math>; já o segundo termo gera uma matriz tridiagonal com diagonal principal nula. Nota-se que os primeiros termos dos dois lados da igualdade são o conjugado um do outro: define-se, portanto, <math>\alpha^n = 1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)</math> e <math>\beta = 1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)</math>. | |||
<center> | |||
<math> | |||
\begin{cases} | |||
\alpha^{n+1}f^{n+1} _j + \dfrac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = | |||
\alpha^{n^*}f^{n} _j - \dfrac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1} ) \\ | |||
\beta^{n+1}g^{n+1} _j + \dfrac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = | |||
\beta^{n^*}g^{n} _j - \dfrac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) | |||
\end{cases} | |||
</math> | |||
</center> | |||
Considerando que o potencial <math>V</math> é só função da posição, escreve-se o método como: | |||
<center> | |||
<math> | |||
\begin{cases} | |||
Af^{n+1} + Bg^{n+1} = A^*f^n - Bg^n \\ | |||
Cg^{n+1} + Bf^{n+1} = C^*g^n - Bf^n \\ | |||
\end{cases} | |||
</math>, | |||
</center> | |||
onde | |||
<center> | |||
<math> | |||
A = \begin{bmatrix} | |||
\alpha & 0 & 0 & \cdots & 0\\ | |||
0 & \alpha & 0 & \cdots & 0 \\ | |||
0 & 0 & \alpha & \cdots & 0 \\ | |||
\vdots & \vdots & \vdots & \ddots & \vdots \\ | |||
0 & \cdots & \cdots & \cdots & \alpha \\ | |||
\end{bmatrix}; \quad | |||
B = \begin{bmatrix} | |||
0 & \frac{\Delta t}{4h} & 0 & \cdots & 0\\ | |||
-\frac{\Delta t}{4h} & 0 & \frac{\Delta t}{4h} & \cdots & 0 \\ | |||
0 & -\frac{\Delta t}{4h} & 0 & \cdots & 0 \\ | |||
\vdots & \vdots & \ddots & \ddots & \vdots \\ | |||
0 & \cdots & \cdots & -\frac{\Delta t}{4h} & 0 \\ | |||
\end{bmatrix}; \quad | |||
C = \begin{bmatrix} | |||
\beta & 0 & 0 & \cdots & 0\\ | |||
0 & \beta & 0 & \cdots & 0 \\ | |||
0 & 0 & \beta & \cdots & 0 \\ | |||
\vdots & \vdots & \vdots & \ddots & \vdots \\ | |||
0 & \cdots & \cdots & \cdots & \beta \\ | |||
\end{bmatrix} | |||
</math>. | |||
</center> | |||
Por fim, pode-se escrever o método resolvendo o sistema | |||
<center> | |||
<math> | |||
\begin{cases} | |||
f^{n+1} = F^{-1}D f^n -F^{-1}E g^n \\ | |||
g^{n+1} = J^{-1}G f^n - J^{-1}H g^n \\ | |||
\end{cases} | |||
</math>, | |||
</center> | |||
onde <math>D = (B^{-1}A^* + C^{-1}B)</math>, <math>E = (I + C^{-1}C^*)</math>, <math>F = (B^{-1}A - C^{-1}B)</math>, <math>G = (A^{-1}A^* + I)</math>, <math>H = (A^{-1}B + B^{-1}C^*)</math> e <math>J= (A^{-1}B - B^{-1}C)</math>. | |||
Com isso, e com condições iniciais e de contorno bem estabelecidas, já é possível aplicar o método, dado que todas essas matrizes dependem somente dos parâmetros do sistema. | |||
===Estabilidade Crank-Nicolson=== | |||
Utilizar-se-á o método de von Neumann para analisar a estabilidade do método de Crank-Nicolson para a equação de Dirac unidimensional. Para tanto, supõe-se que a função <math>\mathbf{\Phi^{n} _j}</math> pode ser dada pela série de Fourier | |||
<center> | |||
<math> | |||
\mathbf{\Phi^{n} _j} = \sum_{k=0}^{\inf} \mathbf{A}^{n}e^{ikqjh} | |||
</math> | |||
</center> | |||
Devido à independência linear de cada termo do somatório, ao substituir na equação do método haverá uma equação para cada ente do somatório. Se <math>\left|\frac{\mathbf{A}^{n+1}}{\mathbf{A}^{n}}\right| \le 1</math>, então pode-se dizer que o método estável, já que dessa forma garante-se uma não divergência. | |||
Aplica-se um termo geral da série de índice <math>k</math> no método CN para a equação de Dirac 1D: | |||
<center> | |||
<math> | |||
\left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{A}^{n+1}e^{ikqjh} + \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n+1}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] = | |||
\left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2\right]\mathbf{A}^{n}e^{ikqjh} - \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] | |||
</math> | |||
</center> | |||
Divide-se tudo por <math>e^{ikqjh}</math> e isola-se <math>\mathbf{A}</math>: | |||
<center> | |||
<math> | |||
\left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n+1}= | |||
\left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n} | |||
</math> | |||
<math> | |||
\left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n+1}= | |||
\left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n} | |||
</math> | |||
<math> | |||
\left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n+1}= | |||
\left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 + \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n} | |||
</math> | |||
</center> | |||
Nota-se que os termos que multiplicam o fator <math>\mathbf{A}</math> são o conjugado um do outro. Define-se <math>z_l</math> como a componente l escalarda multiplicação da matriz <math>I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)</math> pelo vetor <math>A</math>: | |||
<center> | |||
<math> | |||
\frac{{A_l}^{n+1}}{{A_l}^{n}} = \frac{z^*}{z} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\left|\frac{{A_l}^{n+1}}{{A_l}^{n}}\right| = \left|\frac{z^*}{z}\right| = \frac{|z^*|}{|z|} = 1 | |||
</math>, | |||
</center> | |||
onde <math>z</math> é sempre diferente de zero, visto que a parte real é dada por uma matriz identidade constante. | |||
Mostra-se, portanto, que a razão entre os coeficientes da série de Fourier nunca diverge, ou seja, o método é incondicionalmente estável. | |||
==Método Leap-frog== | |||
O método de Leap-frog (LF) é um método explicito, utilizando apenas termos em um mesmo instante do tempo para calcular as derivadas espaciais. Na simulação realizada, utilizou-se a equação de Dirac em duas dimensões com potencial magnético nulo: | |||
<center> | |||
<math> | |||
i \partial_t \mathbf{\Phi} = [-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} | |||
</math> | |||
</center> | |||
Dessa forma, enuncia-se o método LF como: | |||
<center> | |||
<math> | |||
i \partial_t \mathbf{\Phi}_{i,j}^{n} = [-\frac{i}{\varepsilon}(\sigma_1\partial_x+\sigma_2\partial_y) + \frac{1}{\varepsilon^2}\sigma_3] \mathbf{\Phi}_{i,j}^{n} + [V(t,x)I_2] \mathbf{\Phi}_{i,j}^{n} | |||
</math> | |||
</center> | |||
De forma análoga ao cada de uma dimensão, é feita a discretização temporal e espacial. Utiliza-se a discretização temporal como $t_n=t0+n\delta t$ na dimensão $y$ na forma $y_j=y_0+jh$ e na dimensão $x$ como $x_i=x_0+ih$, onde $j$ e $i$ são números inteiros. Em adição, discretiza-se as derivadas espaciais e temporal da seguinte forma: | |||
<center> | |||
<math> | |||
\delta_t\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n+1} _{i,j}} - \mathbf{\Phi^{n-1} _{i,j}}}{2\Delta t} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\delta_x\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n} _{i+1,j}} - \mathbf{\Phi^{n} _{i-1,j}}}{2h} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
\delta_y\mathbf{\Phi^n _{i,j}} = \frac{\mathbf{\Phi^{n} _{i,j+1}} - \mathbf{\Phi^{n} _{i,j-1}}}{2h} | |||
</math> | |||
</center> | |||
Primeiramente, reescreve-se o método na forma escalar como: | |||
<center> | |||
<math> | |||
i \partial_t {\Phi_1}_{i,j}^{ n} = -\frac{i}{\varepsilon}(\partial_x-i\partial_y) {\Phi_4}_{i,j}^{n} + \frac{1}{\varepsilon^2}{\Phi_1}_{i,j}^{n} + V(t,x){\Phi_1}_{i,j}^{n} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
i \partial_t {\Phi_4}_{i,j}^{n} = -\frac{i}{\varepsilon}(\partial_x+i\partial_y) {\Phi_1}_{i,j}^{n} - \frac{1}{\varepsilon^2}{\Phi_4}_{i,j}^{n} + V(t,x){\Phi_4}_{i,j}^{n} | |||
</math> | |||
</center> | |||
Substituindo-se as derivadas pela forma discreta, e isolando-se o termo do passo termoral posterior, obtêm-se a forma final como: | |||
<center> | |||
<math> | |||
{\Phi_1}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon}[({\Phi_4}_{i+1,j}^{n}-{\Phi_4}_{i-1,j}^{n})-i({\Phi_4}_{i,j+1}^{n}-{\Phi_4}_{i,j-1}^{n})]-2i\Delta t[\frac{1}{\varepsilon^2}+V_{i,j}^{n}]{\Phi_1}_{i,j}^{n}+{\Phi_1}_{i,j}^{n-1} | |||
</math> | |||
</center> | |||
<center> | |||
<math> | |||
{\Phi_4}_{i,j}^{n+1}=-\frac{\Delta t}{h\varepsilon}[({\Phi_1}_{i+1,j}^{n}-{\Phi_1}_{i-1,j}^{n})+i({\Phi_1}_{i,j+1}^{n}-{\Phi_1}_{i,j-1}^{n})]+2i\Delta t[\frac{1}{\varepsilon^2}+V_{i,j}^{n}]{\Phi_4}_{i,j}^{n}+{\Phi_4}_{i,j}^{n-1} | |||
</math> | |||
</center> | |||
===Estabilidade do Método Leap-frog=== | |||
Assumindo que o potencial <math>V</math> é independente do tempo, pode-se provar via método de von Neumann que o método de Leap-frog é estável sobre as condições: | |||
<center> | |||
<math> | |||
0 < \Delta t \leq \frac{\varepsilon^2 h}{|V|\varepsilon^2h+\sqrt{h^2+\varepsilon^2}} | |||
</math> | |||
</center> | |||
Para <math> h>0 </math> e <math> 0<\varepsilon \leq 1. </math> [[Equação_de_Dirac#Referências|(2)] | |||
=Simulações em Julia= | |||
==Equação 1D== | |||
Fez-se simulações do método de Crank-Nicolson para a equação de Dirac unidimensional em três configurações de potenciais diferentes: Nulo (Partícula Livre), Poço Infinito e Oscilador Harmônico Simples. | |||
Para todos os casos utilizou-se uma condição inicial de um pacote gaussiano de desvio padrão <math>\sigma</math> para uma das componentes de <math>\mathbf{\Phi}</math>, sendo a outra componente nula. O módulo quadrado do pacote gaussiano deve ter área unitária dentro da malha utilizada (de <math>x=0</math> até <math>x=50</math>), por isso a constante de normalização deve ser <math>\frac{1}{\sqrt{\sigma\sqrt{\pi}}}</math>. | |||
Segue trecho do código comum a todos as simulações realizadas; a única diferença é que em um caso do OHS o pacote gaussiano é deslocado do meio da malha para a posição <math>x=18</math>. | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
using LaTeXStrings | |||
using LinearAlgebra | |||
using Integrals | |||
function init(x, sigma) | |||
arg1 = @. ((-(x-25)^2)/(2*sigma^2)) | |||
arg2 = 1/sqrt(sqrt(pi)*sigma) | |||
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano | |||
end | |||
function OHS(V,x, k) | |||
V = @. 0.5*k*(x-25)^2 | |||
return V | |||
end | |||
function poco(V, h) | |||
#Quero colocar nas posições 18 e 32 | |||
V[round(Int64, 18/h)] = 100000 | |||
V[round(Int64, 32/h)] = 100000 | |||
return V | |||
end | |||
##Matrizes do método de Crank-Nicholson | |||
function matriz(dt,h,L, V) | |||
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.+1))) | |||
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h))) | |||
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.-1))) | |||
A = Array(A) | |||
B = Array(B) | |||
C = Array(C) | |||
A_i = inv(A) | |||
B_i = inv(B) | |||
C_i = inv(C) | |||
AiB = A_i*B | |||
CiB = C_i*B | |||
D = B_i*conj(A) + CiB | |||
E = I(L) + C_i*conj(C) | |||
F = B_i*A -CiB | |||
G = A_i*conj(A) + I(L) | |||
H = AiB + B_i*conj(C) | |||
J = AiB - B_i*conj(C) | |||
F_i = inv(F) | |||
J_i = inv(J) | |||
K = F_i*D | |||
L = F_i*E | |||
M = J_i*G | |||
N = J_i*H | |||
return K, L, M, N | |||
end | |||
function CN(size, h, tsize, V, dt, ci) | |||
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1 | |||
g = zeros(Complex, tsize, size) ##phi 4 | |||
A, B, C, D = matriz(dt, h, size, V) #Matrizes do método Crank-Nicholson | |||
f[1, :] = ci ##Condição Inicial | |||
g[1, :] = zeros(size) | |||
##Condições de Contorno | |||
f[:, 1] = zeros(tsize) | |||
f[:, end] = zeros(tsize) | |||
g[:, 1] = zeros(tsize) | |||
g[:, end] = zeros(tsize) | |||
i=2 #Não interfiro nos contornos | |||
while i<tsize | |||
f[i, :] = A*f[i-1, :] - B*g[i-1, :] | |||
g[i, :] = C*f[i-1, :] - D*g[i-1, :] | |||
i+=1 | |||
end | |||
return f, g | |||
end | |||
</source><br /> | |||
===Partícula Livre=== | |||
Aplicou-se o código demonstrado com potencial nulo para simular o caso da partícula livre. Segue abaixo código utilizado para gerar a animação: | |||
[[Arquivo:Diracfree.gif]] | |||
Nota-se que mesmo que <math>\phi_4</math> seja nula no início, a existência da partícula <math>\phi_1</math> (neste caso, o elétron com spin up) gera a outra (pósitron com spin down). O comportamento é de dispersão, ou seja, a tendência é que a posição fique cada vez menos definida: a partícula livre, por estar fora da ação de um potencial, apresenta momento bem definido; pelo Princípio da Incerteza, a posição torna-se incerta. Nota-se também que as bordas estão longe o suficiente na escala de tempo utilizada, de maneira que as condições de contorno não afetam a simulação. | |||
<br /> | |||
<source lang="julia"> | |||
function main() | |||
L = 50 #Dimensão espacial matriz | |||
k=0.1 #"Constante Elástica" do oscilador harmônico | |||
sigma = 1 #Largura do pacote gaussiano | |||
dt = 0.02 | |||
size= 10*L | |||
h = L/size ##Passo espacial | |||
tmax = 15 | |||
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo | |||
t = LinRange(0, tmax, tsize) | |||
x = LinRange(0, L, size) | |||
V = zeros(size) | |||
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano | |||
f,g =CN(size,h,tsize, V, dt,xi) | |||
i=1 | |||
anim = @animate while i<=tsize | |||
f_real = real(f[i, :]) | |||
f_imag = imag(f[i, :]) | |||
g_real = real(g[i, :]) | |||
g_imag = imag(g[i, :]) | |||
probf = abs2.(f[i, :]) | |||
probg = abs2.(g[i, :]) | |||
prob = probf + probg | |||
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15)) | |||
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15)) | |||
titulo = "Partícula Livre"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3)) | |||
plot!(title=titulo, | |||
xlabel = "x", | |||
xlim=(0,50), | |||
xticksfont = font(13), | |||
ticksfontsize = 10, | |||
ylim=(0,1), | |||
yticksfont=font(13), | |||
) | |||
i+=1 | |||
end | |||
arquivo = "diracfree.gif" | |||
gif(anim, arquivo, fps=30) | |||
end | |||
main() | |||
</source><br /> | |||
===Poço Infinito=== | |||
O poço infinito foi simulado colocando dois potenciais muito grandes em <math>x=18</math> e <math>x=32</math>. Abaixo está reproduzida a animação. | |||
[[Arquivo:Diracpoco.gif]] | |||
Nota-se que a função simulada é a soma dos quadrados dos módulos de cada função de onda (elétron e pósitron); é a integral de <math>|\Phi|^2 = |\phi_1|^2+|\phi_4|^2</math> que deve sempre ser unitária, o que concorda com o obtido. Na animação é possível perceber um comportamento semelhante ao de uma onda estacionária, onde tem-se vários "harmônicos" associados ao pacote de ondas: como esperado, a função de onda é uma combinação linear dos autoestados do poço infinito. | |||
Segue trecho do código utilizado para gerar a animação: | |||
<br /> | |||
<source lang="julia"> | |||
function main() | |||
L = 50 #Dimensão espacial matriz | |||
sigma = 1 #Largura do pacote gaussiano | |||
dt = 0.05 #Passo temporal | |||
size= 30*L #Utilizado para definir o passo espacial | |||
h = L/size #Passo espacial | |||
tmax = 30 # | |||
tsize = round(Int64, tmax/dt) tamanho do vetor tempo. | |||
t = LinRange(0, tmax, tsize) | |||
x = LinRange(0, L, size) | |||
V = zeros(size) | |||
xi = init(LinRange(0, L, size), sigma) #Condição inicial de pacote gaussiano centralizado em x=25 | |||
#V = OHS(V,x,k) | |||
V = poco(V, h) #Inicializa o potencial | |||
f,g =CN(size,h,tsize, V, dt,xi) #Obtém as funções de onda e sua respectiva evolução temporal | |||
##Produz-se a animação | |||
i=1 | |||
anim = @animate while i<=tsize | |||
f_real = real(f[i, :]) | |||
f_imag = imag(f[i, :]) | |||
g_real = real(g[i, :]) | |||
g_imag = imag(g[i, :]) | |||
probf = abs2.(f[i, :]) | |||
probg = abs2.(g[i, :]) | |||
prob = probf + probg | |||
problem = SampledIntegralProblem(prob, x) #Resolve a integral em cada tempo, calculando a área e mostrando na animação | |||
method = TrapezoidalRule() | |||
integral = solve(problem, method) | |||
integral = round(integral[1]; digits=3) #Arredonda. | |||
integral = string(integral) | |||
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2) | |||
titulo = "Poço Infinito"*", "*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral | |||
plot!(x,V, label="Potencial", legendfont=font(15)) | |||
plot!(title=titulo, | |||
xlabel = "x", | |||
xlim=(15,35), | |||
xticksfont = font(13), | |||
ticksfontsize = 10, | |||
ylim=(0,0.6), | |||
yticksfont=font(13), | |||
) | |||
i+=2 ##O passo é dado de 2 em 2 para deixar gif mais leve. | |||
end | |||
arquivo = "diracpoco.gif" | |||
gif(anim, arquivo, fps=30) | |||
end | |||
main() | |||
</source><br /> | |||
===Oscilador Harmônico Simples=== | |||
Inicialmente, realizou-se a simulação deslocando o pacote gaussiano para a posição inicial <math>x=18</math>, com a finalidade de observar a oscilação. Testou-se a simulação com diferentes <math>k</math>'s; escolheu-se o que está mostrado abaixo pois facilita a visualização do comportamento oscilatório. | |||
[[Arquivo:DiracOHS.gif]] | |||
Nota-se um comportamento análogo ao caso clássico; porém, em alguns momentos é possível observar certos harmônicos do pacote de onda. Além disso, nota-se nas extremidades um valor máximo para <math>|\mathbf{\Phi}|^2</math>, também condizente com o caso clássico. | |||
Durante testes nas simulações, notou-se que a área sob a curva possui variações quando se utiliza um passo <math>\Delta t</math> muito alto. Nesse caso, a convergência do método de Crank-Nicolson para os valores teóricos depende da malha utilizada, embora a estabilidade dele seja incondicional. A diferença pode ser vista comparando-se a animação abaixo com a anterior: | |||
[[Arquivo:DiracOHSdtalto.gif]] | |||
Em seguida, passou-se para uma condição inicial com um pacote gaussiano centralizado: | |||
[[Arquivo:DiracOHScentral.gif]] | |||
Mesmo que a posição inicial esteja no centro, devido ao fato da posição não estar bem definida ocorrem pequenas oscilações em torno do ponto de equilíbrio. | |||
Por fim, segue o código utilizado para o oscilador harmônico simples (a diferença entre cada caso é só as constantes e a condição inicial). | |||
<br /> | |||
<source lang="julia"> | |||
function main() | |||
L = 50 #Dimensão espacial matriz | |||
k=0.1 #"Constante Elástica" do oscilador harmônico | |||
sigma = 1 #Largura do pacote gaussiano | |||
dt = 0.02 | |||
size= 10*L | |||
h = L/size ##Passo espacial | |||
tmax = 50 | |||
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo | |||
t = LinRange(0, tmax, tsize) | |||
x = LinRange(0, L, size) | |||
V = zeros(size) | |||
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano | |||
V = OHS(V,x,k) ##inicializa o potencial | |||
f,g =CN(size,h,tsize, V, dt,xi) | |||
i=1 | |||
#Faz o gif | |||
anim = @animate while i<=tsize | |||
f_real = real(f[i, :]) | |||
f_imag = imag(f[i, :]) | |||
g_real = real(g[i, :]) | |||
g_imag = imag(g[i, :]) | |||
probf = abs2.(f[i, :]) | |||
probg = abs2.(g[i, :]) | |||
prob = probf + probg | |||
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva | |||
method = TrapezoidalRule() | |||
integral = solve(problem, method) | |||
integral = round(integral[1]; digits=3) | |||
integral = string(integral) | |||
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2) | |||
#= | |||
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15)) | |||
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15)) | |||
=# | |||
titulo = "OHS"*", "*L"$k=$"*string(k)*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral | |||
plot!(x,V, label="Potencial", legendfont=font(15)) | |||
plot!(title=titulo, | |||
xlabel = "x", | |||
xlim=(0,50), | |||
xticksfont = font(13), | |||
ticksfontsize = 10, | |||
ylim=(0,1), | |||
yticksfont=font(13), | |||
) | |||
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve | |||
end | |||
arquivo = "diracOHS.gif" | |||
gif(anim, arquivo, fps=30) | |||
end | |||
main() | |||
</source><br /> | |||
==Equação 1D com potencial "escalar"== | |||
Por fim, consideraremos o problema com o potencial "escalar" <math>V_{sc}</math>. Dentro do formalismo da relatividade, os potenciais podem ser classificados de acordo com o seu comportamento frente a uma transformação de Poincaré: o potencial <math>V</math> se transforma como um vetor (por isso chamado de potencial "vetor"), e o potencial <math>V_{sc}</math>, como um escalar (potencial "escalar"). Como exemplo de potencial do tipo vetor, temos os potenciais eletromagnéticos; e de potencial do tipo escalar, pode-se citar modelos de confinamento. Na prática, pode-se dizer que o potencial <math>V_{sc}</math> altera a massa de repouso "efetiva" da partícula. Para este assunto, deixamos [[Equação_de_Dirac#Referências|(4)]] e [[Equação_de_Dirac#Referências|(5)]] como referências. | |||
Por ser um tópico bastante especializado, será considerado aqui apenas o caso do poço infinito. O problema é apenas uma extensão do que foi exposto [[Equação_de_Dirac#Poço Infinito|nessa seção]]; a [[Equação_de_Dirac#Método_de_Crank-Nicolson|discretização]] e a estabilidade do método de Crank-Nicolson são análogas, bastando apenas fazer <math>\alpha^n = 1 + \frac{i \Delta t}{2}(V^n _j + V_{{sc}_j}^n + 1)</math> e <math>\beta^n = 1 + \frac{i \Delta t}{2}(V^n _j - V_{{sc}_j}^n -1)</math>. | |||
===Poço Infinito=== | |||
Fez-se uma simulação completamente análoga à anterior, mas usando <math>V=0</math> e definindo o poço infinito em <math>V_{sc}</math>. A animação está reproduzida abaixo. | |||
[[Arquivo:DiracVscPoco.gif]] | |||
Não há diferença notável com relação ao poço infinito em <math>V</math>: o confinamento da partícula não muda, mesmo que a sua massa de repouso "efetiva" sim. No entanto, ressalta-se que esse é o comportamento conjunto das duas componentes <math>\phi_1</math> e <math>\phi_4</math>; o comportamento individual de cada uma pode ser diferente. | |||
Em seguida, foi feita uma simulação colocando o poço infinito nos dois potenciais, ou seja, fazendo <math>V=V_{sc}</math>, conforme animação abaixo. | |||
[[Arquivo:DiracVscVPoco.gif]] | |||
Dessa vez, o comportamento é bastante diferente: a partícula fica apenas parcialmente confinada no poço, sendo parte da função de onda transmitida. Assim, observa-se um fenômeno que não ocorre na formulação não relativística da Mecânica Quântica: o de tunelamento em uma barreira infinita. | |||
Segue abaixo o código utilizado para produzir as animações, adaptado do código utilizado [[Equação_de_Dirac#Poço Infinito|aqui]]. A diferença entre as duas animações é de apenas uma linha, definindo <math>V=0</math> ou <math>V=V_{sc}</math>. | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
using LaTeXStrings | |||
using LinearAlgebra | |||
using Integrals | |||
function init(x, sigma) | |||
arg1 = @. ((-(x-25)^2)/(2*sigma^2)) | |||
arg2 = 1/sqrt(sqrt(pi)*sigma) | |||
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano | |||
end | |||
function poco(V, h) | |||
#Quero colocar nas posições 18 e 32 | |||
V[round(Int64, 18/h)] = 100000 | |||
V[round(Int64, 32/h)] = 100000 | |||
return V | |||
end | |||
##Matrizes do método de Crank-Nicholson | |||
function matriz(dt,h,L, V, Sc) | |||
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V+Sc.+1))) | |||
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h))) | |||
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V-Sc.-1))) | |||
A = Array(A) | |||
B = Array(B) | |||
C = Array(C) | |||
A_i = inv(A) | |||
B_i = inv(B) | |||
C_i = inv(C) | |||
AiB = A_i*B | |||
CiB = C_i*B | |||
D = B_i*conj(A) + CiB | |||
E = I(L) + C_i*conj(C) | |||
F = B_i*A -CiB | |||
G = A_i*conj(A) + I(L) | |||
H = AiB + B_i*conj(C) | |||
J = AiB - B_i*conj(C) | |||
F_i = inv(F) | |||
J_i = inv(J) | |||
K = F_i*D | |||
L = F_i*E | |||
M = J_i*G | |||
N = J_i*H | |||
return K, L, M, N | |||
end | |||
function CN(size, h, tsize, V, Sc, dt, ci) | |||
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1 | |||
g = zeros(Complex, tsize, size) ##phi 4 | |||
A, B, C, D = matriz(dt, h, size, V, Sc) #Matrizes do método Crank-Nicholson | |||
f[1, :] = ci ##Condição Inicial | |||
g[1, :] = zeros(size) | |||
##Condições de Contorno | |||
f[:, 1] = zeros(tsize) | |||
f[:, end] = zeros(tsize) | |||
g[:, 1] = zeros(tsize) | |||
g[:, end] = zeros(tsize) | |||
i=2 #Não interfiro nos contornos | |||
while i<tsize | |||
f[i, :] = A*f[i-1, :] - B*g[i-1, :] | |||
g[i, :] = C*f[i-1, :] - D*g[i-1, :] | |||
i+=1 | |||
end | |||
return f, g | |||
end | |||
function main() | |||
L = 50 #Dimensão espacial matriz | |||
sigma = 1 #Largura do pacote gaussiano | |||
dt = 0.02 | |||
size= 10*L | |||
h = L/size ##Passo espacial | |||
tmax = 50 | |||
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo | |||
t = LinRange(0, tmax, tsize) | |||
x = LinRange(0, L, size) | |||
V = zeros(size) | |||
Sc = copy(V) | |||
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano | |||
Sc = poco(Sc,h) ##potencial "escalar" | |||
V = copy(Sc) ##potencial "vetor" | |||
f,g = CN(size,h,tsize,V,Sc,dt,xi) | |||
i=1 | |||
#Faz o gif | |||
anim = @animate while i<=tsize | |||
f_real = real(f[i, :]) | |||
f_imag = imag(f[i, :]) | |||
g_real = real(g[i, :]) | |||
g_imag = imag(g[i, :]) | |||
probf = abs2.(f[i, :]) | |||
probg = abs2.(g[i, :]) | |||
prob = probf + probg | |||
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva | |||
method = TrapezoidalRule() | |||
integral = solve(problem, method) | |||
integral = round(integral[1]; digits=3) | |||
integral = string(integral) | |||
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2) | |||
titulo = "Poço"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral | |||
plot!(x,Sc, label=L"$V=V_{sc}$", legendfont=font(15)) | |||
plot!(title=titulo, | |||
xlabel = "x", | |||
xlim=(0,50), | |||
xticksfont = font(13), | |||
ticksfontsize = 10, | |||
ylim=(0,1), | |||
yticksfont=font(13), | |||
) | |||
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve | |||
end | |||
arquivo = "diracVscVPoco.gif" | |||
gif(anim, arquivo, fps=30) | |||
end | |||
main() | |||
</source><br /> | |||
==Equação 2D== | |||
Utilizou-se o método de Leap-Frog para simulação da equação de Dirac bidimensional em um potencial Coulombiano central e em um potencial cossenoide. Em ambos casos, o potencial não depende do tempo e a condição inicial constituiu-se de um pacote gaussiano, centralizado em <math>(0,0)</math> para <math>\Phi_1</math> e em <math>(1,1)</math> para <math>\Phi_4</math>. De forma aproximada, atribuiu-se para o passo temporal seguinte: | |||
<center> | |||
<math> | |||
\mathbf{\Phi}_{i,j}^{1}=\mathbf{\Phi}_{i,j}^{0} -sin(\frac{\Delta t }{\varepsilon})\sigma_1(\delta_x+\delta_y)\mathbf{\Phi}_{i,j}^{0}-i(sin(\frac{\Delta t }{\varepsilon^2})\sigma_3+\Delta t V_{i,j}^{0} I_2)\mathbf{\Phi}_{i,j}^{0} | |||
</math> | |||
</center> | |||
Segue abaixo o código utilizado para ambos potenciais, o qual seu uso difere apenas em qual potencial foi comentado: | |||
<br /> | |||
<source lang="julia"> | |||
using Plots | |||
using LinearAlgebra | |||
function initial_values() | |||
L=10 #Malha de 4*(L/h)² de -L a L nas duas dimensões | |||
h=1/16 #dx,dy=h | |||
dt=0.01 | |||
ep=0.8 #0<ep<=1 -> := v/c | |||
x=LinRange(-L,L,2*Int(L/h)) | |||
y=LinRange(-L,L,2*Int(L/h)) | |||
#Potencial Coulombiano | |||
V= zeros(ComplexF64,2*Int(L/h),2*Int(L/h)) | |||
Qe=1. | |||
K=1 #K=9*10^9 | |||
V = [ -K*Qe/sqrt((x[i]^2 + y[j]^2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ] | |||
#Potencial Cossenoide | |||
#V = [ cos((-4*pi/sqrt(3))*x[i])+cos((2*pi/sqrt(3))*x[i]+2*pi*y[j])+cos((2*pi/sqrt(3))*x[i]-2*pi*y[j]) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ] | |||
#psi 1 inicial (t=0) | |||
psi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h)) | |||
psi1 = [ (exp(-((x[i])^2+(y[j])^2)/2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ] | |||
#psi4 iniciall (t=0) | |||
psi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h)) | |||
psi4 = [ exp(-((x[i] -1 )^2+(y[j] -1)^2)/2) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ] | |||
#próximo psi1 (t=0+dt) | |||
nextpsi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h)) | |||
j=2 | |||
while j < 2*Int(L/h) | |||
i=2 | |||
while i < 2*Int(L/h) | |||
nextpsi1[i,j] = psi1[i,j]-sin(dt/ep)*((psi4[i+1,j]-psi4[i-1,j]) + (psi4[i,j+1]-psi4[i,j-1]))/(2*h)-im*(-im*sin(dt/(ep^2))*psi4[i,j]+h*V[i,j]*psi1[i,j]) | |||
i+=1 | |||
end | |||
j+=1 | |||
end | |||
#próximo psi4 (t=0+dt) | |||
nextpsi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h)) | |||
j=2 | |||
while j < 2*Int(L/h) | |||
i=2 | |||
while i < 2*Int(L/h) | |||
nextpsi4[i,j]= psi4[i,j]-sin(dt/ep)*((psi1[i+1,j]-psi1[i-1,j]) + (psi1[i,j+1]-psi1[i,j-1]))/(2*h)-im*(im*sin(dt/(ep^2))*psi1[i,j]+h*V[i,j]*psi4[i,j]) | |||
i+=1 | |||
end | |||
j+=1 | |||
end | |||
return L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4 | |||
end | |||
L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4=initial_values() | |||
#listas para salvar os frames do gif | |||
anim_psi1=[] | |||
anim_psi4=[] | |||
#cópia para manipulação | |||
uu=deepcopy(psi1) | |||
vv=deepcopy(psi4) | |||
t=0; tmax=5 | |||
while t < tmax | |||
global j | |||
global uu; global vv; | |||
global u; global v; | |||
u=deepcopy(nextpsi1) | |||
v=deepcopy(nextpsi4) | |||
j=2 | |||
while j < 2*Int(L/h) | |||
global i=2 | |||
while i < 2*Int(L/h) | |||
global i | |||
nextpsi1[i,j]= -(dt/(ep*h))*(v[i+1,j]-v[i-1,j])+((im*dt)/(ep*h))*(v[i,j+1]-v[i,j-1])-((2*im*dt)/(ep^2))*u[i,j]-(2*dt*im)*V[i,j]*u[i,j]+uu[i,j] | |||
nextpsi4[i,j]= -(dt/(ep*h))*(u[i+1,j]-u[i-1,j])-((im*dt)/(ep*h))*(u[i,j+1]-u[i,j-1])+((2*im*dt)/(ep^2))*v[i,j]+(2*dt*im)*V[i,j]*v[i,j]+vv[i,j] | |||
i+=1 | |||
end | |||
j+=1 | |||
end | |||
uu=deepcopy(u) | |||
vv=deepcopy(v) | |||
global t+=dt | |||
push!(anim_psi1,deepcopy(nextpsi1)) | |||
push!(anim_psi4,deepcopy(nextpsi4)) | |||
end | |||
using LaTeXStrings | |||
using Printf | |||
#montagem do gif | |||
function psi_anim(x,y,psi,tmax) | |||
i=1 | |||
anim = @animate while i<=length(psi) | |||
psi_real = real.(psi[i]) | |||
psi_imag = imag.(psi[i]) | |||
prob = abs2.(psi[i]) | |||
t=0.01*i | |||
titulo="Potencial Coulombiano, "*L"| \Phi |^{2}"*@sprintf("em t=%0.2f",t) | |||
#titulo=@sprintf("| \Phi |^{2}em t = %f", | |||
u=2*L/h #exibe a malha de forma reduzida | |||
p = surface(x[Int(u/4):Int(3*u/4)],y[Int(u/4):Int(3*u/4)],prob[Int(u/4):Int(3*u/4),Int(u/4):Int(3*u/4)],title=titulo, xlabel = "x",ylabel="y",zlabel="Densidade de Probabilidade" ,zlim=(-1,1),clim=(0, maximum(psi_real))) | |||
i+=1 | |||
end | |||
arquivo = "dirac2D.gif" | |||
gif(anim, arquivo, fps=30) | |||
end | |||
psi_anim(x,y,anim_psi1,tmax) | |||
</source><br /> | |||
===Potencial Coulombiano=== | |||
Na animação gerada, nota-se o padrão de dispersão para o infinito, pois o potencial escolhido varia de positivamente no caso escolhido. Observa-se um padrão de ruído na parte central, o qual não foi estudado afundo, mas é exclusivo de pontos próximos à um ponto de divergência da função potencial. | |||
===Potencial Cossenoide=== | |||
Reproduziu-se o potencial estudado para representações do grafeno em um único plano. Observa-se, no período de tempo exibido, que padrões de ruído não são encontrados e a tendência para o infinito permanece. | |||
=Referências= | =Referências= | ||
# The quantum theory of the electron. Proceedings of the Royal Society of London | # The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928. | ||
# SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012. | # SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012. | ||
# BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017. | # BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017. | ||
# SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973. | |||
# THALLER, B. The Dirac equation. Berlin: Springer, 2010. | |||
Edição atual tal como às 18h41min de 12 de maio de 2024
Grupo: André Luis Della Valentina, Lucas dos Santos Assmann, Vinícius Bayne Müller
Introdução
A equação de Dirac descreve uma partícula relativística de spin , como o elétron, com estrutura análoga a da equação de Schrödinger. Ela surgiu inicialmente como tentativa de explicar discrepâncias entre experimentos e teoria para o espectro do átomo de hidrogênio, possibilitando correções para o cálculo da energia do elétron em diferentes níveis (as chamadas correções de estrutura fina). Além disso, por meio dela foi possível prever a existência de antimatéria: descrevendo o elétron, ela também descreve o pósitron.
A fim de compatibilizar a Mecânica Quântica com a Relatividade Especial, a equação diferencial parcial é de primeira ordem tanto no tempo quanto no espaço (diferentemente da equação de Schrödinger, que é de segunda ordem no espaço). A equação de Dirac pode ser escrita de diversas formas; aqui, apresentamo-la explicitamente como um sistema de EDPs acopladas, mais conveniente para os propósitos do trabalho.
Assim como a equação de Schrödinger, a construção da equação de Dirac vem a partir do operador Hamiltoniano, que descreve a evolução temporal do estado quântico em questão:
onde, como anteriormente, os autovalores de correspondem aos valores possíveis de energia que o sistema pode assumir.
A mudança com relação à Mecânica Quântica não relativística acontece quando consideramos a energia relativística da partícula:
Assim, o Hamiltoniano é modificado para representar a medida da energia relativística total.
Diferentemente da equação de Schrödinger, aqui não representa apenas uma função de onda, mas sim um conjunto de quatro delas. Usando a notação
,
as componentes de representam as funções de onda associadas ao elétron e ao pósitron: () representa a função de onda do elétron com spin up (down), e () representa a função de onda do pósitron com spin up (down). O objeto é chamado de spinor.
Dedução da equação de Dirac em uma e duas dimensões
Consideraremos neste trabalho a equação de Dirac em uma e duas dimensões, e . A escolha dessas coordenadas se dá pela conveniência do acoplamento das EDPs: nesse caso, as quatro equações acopladas passam a ser acopladas duas a duas, facilitando o estudo do sistema. A dedução aqui apresentada é baseada em (1) e (2).
Construção do Hamiltoniano completo
Consideremos uma partícula sob ação de um potencial (onde ), que afeta a energia potencial da partícula, e de um potencial "escalar" , que afeta a massa de repouso da mesma. Seguindo uma das propostas possíveis para o Hamiltoniano, temos
onde ; e são matrizes 4x4 adimensionais e é o vetor momento linear da partícula.
Pode-se mostrar que e devem satisfazer certos vínculos, limitando as escolhas possíveis para essas matrizes. A escolha mais simples e usualmente adotada consiste em tomar
Sendo , podemos escrever o produto escalar como
Portanto, em notação matricial o Hamiltoniano pode ser escrito como
Unidades naturais e redução para duas dimensões
A fim de simplificar o formalismo, adotamos as chamadas "unidades naturais", onde . Note que isso equivale a reescalar as quantidades físicas do problema por um fator adequado. Ao fazer , também assumimos que a partícula está no limite relativístico.
Além disso, queremos estudar o problema em duas dimensões. Observamos que ; logo, . Portanto, temos o Hamiltoniano simplificado
Forma explícita final
Retornando ao problema original, queremos resolver
Novamente utilizando a notação matricial, obtemos
Realizando a multiplicação matricial, pode-se ver que se obtém dois sistemas acoplados: com e com . Escolhendo o sistema de com :
Simplificando e isolando a derivada temporal, obtemos por fim
Por fim, a equação em uma dimensão () é facilmente obtida: basta fazer
Neste trabalho, serão considerados principalmente problemas apenas com o potencial ; assim, caso indicado o contrário, será assumido .
Discretização
A equação de Dirac 1D pode ser escrita, na forma matricial, como
onde e é matriz identidade de dimensão 2. As matrizes de Pauli são escritas, aqui, como e .
Para discretizar uma equação diferencial parcial como essa, é necessário discretizar o espaço e o tempo. Convenciona-se como um passo finito de tempo e como um passo finito no espaço, de tal forma que , onde são números inteiros. Define-se a notação e também . Discretiza-se as derivadas parciais explicitamente com uma expansão em série de taylor da própria função:
Considerando uma derivada discretizada e truncando na primeira ordem:
O processo é completamente análogo para a derivada espacial, porém para facilitar a aplicação do método mantém-se o espaço centrado em , em outras palavras faz-se uma expansão em torno de , obtendo:
Com isso, obtém-se uma equação para um método explícito no tempo da equação de Dirac 1D.
Pode-se também desenvolver um método implícito no tempo fazendo a expansão de em torno de , obtendo:
Ao aplicar esta aproximação na equação discretizada basta dar um passo a frente em todos os elementos, obtendo um método implícito no tempo, já que há dependência com .
Neste trabalho, foram utilizados dois métodos de integração numérica diferentes: o de Crank-Nicolson, para a equação de Dirac em uma dimensão, e o de Leap-Frog, para a equação em duas dimensões. Deixamos (3) como referência para estes e outros métodos numéricos aplicados ao problema.
Método de Crank-Nicolson
O método de Crank-Nicolson (CN) consiste em uma média entre um método explícito e outro implícito no espaço. Utilizar-se-á a notação para representar justamente a média entre ambos os métodos, ou seja:
Define-se a notação:
Dessa maneira, enuncia-se o método CN para a equação de Dirac 1D como:
,
onde são as discretizações explícitas das derivadas.
Para que seja possível aplicar e estudar o método, é necessário passar da notação matricial para escalar:
Isolando cada tempo em um lado da igualdade:
Abrindo as matrizes e e operando-as sobre o vetor na equação, tem-se:
Pode-se realizar as operações matriciais e escrever duas equações escalares. Para facilitar a notação, utiliza-se e :
Tem-se então um número de equações onde é o número de elementos do espaço discretizado. Portanto o primeiro termo das duas equações gera uma matriz diagonal, pois multiplica os termos espaciais dependentes de ; já o segundo termo gera uma matriz tridiagonal com diagonal principal nula. Nota-se que os primeiros termos dos dois lados da igualdade são o conjugado um do outro: define-se, portanto, e .
Considerando que o potencial é só função da posição, escreve-se o método como:
,
onde
.
Por fim, pode-se escrever o método resolvendo o sistema
,
onde , , , , e .
Com isso, e com condições iniciais e de contorno bem estabelecidas, já é possível aplicar o método, dado que todas essas matrizes dependem somente dos parâmetros do sistema.
Estabilidade Crank-Nicolson
Utilizar-se-á o método de von Neumann para analisar a estabilidade do método de Crank-Nicolson para a equação de Dirac unidimensional. Para tanto, supõe-se que a função pode ser dada pela série de Fourier
Devido à independência linear de cada termo do somatório, ao substituir na equação do método haverá uma equação para cada ente do somatório. Se , então pode-se dizer que o método estável, já que dessa forma garante-se uma não divergência.
Aplica-se um termo geral da série de índice no método CN para a equação de Dirac 1D:
Divide-se tudo por e isola-se :
Nota-se que os termos que multiplicam o fator são o conjugado um do outro. Define-se como a componente l escalarda multiplicação da matriz pelo vetor :
,
onde é sempre diferente de zero, visto que a parte real é dada por uma matriz identidade constante.
Mostra-se, portanto, que a razão entre os coeficientes da série de Fourier nunca diverge, ou seja, o método é incondicionalmente estável.
Método Leap-frog
O método de Leap-frog (LF) é um método explicito, utilizando apenas termos em um mesmo instante do tempo para calcular as derivadas espaciais. Na simulação realizada, utilizou-se a equação de Dirac em duas dimensões com potencial magnético nulo:
Dessa forma, enuncia-se o método LF como:
De forma análoga ao cada de uma dimensão, é feita a discretização temporal e espacial. Utiliza-se a discretização temporal como $t_n=t0+n\delta t$ na dimensão $y$ na forma $y_j=y_0+jh$ e na dimensão $x$ como $x_i=x_0+ih$, onde $j$ e $i$ são números inteiros. Em adição, discretiza-se as derivadas espaciais e temporal da seguinte forma:
Primeiramente, reescreve-se o método na forma escalar como:
Substituindo-se as derivadas pela forma discreta, e isolando-se o termo do passo termoral posterior, obtêm-se a forma final como:
Estabilidade do Método Leap-frog
Assumindo que o potencial é independente do tempo, pode-se provar via método de von Neumann que o método de Leap-frog é estável sobre as condições:
Para e [[Equação_de_Dirac#Referências|(2)]
Simulações em Julia
Equação 1D
Fez-se simulações do método de Crank-Nicolson para a equação de Dirac unidimensional em três configurações de potenciais diferentes: Nulo (Partícula Livre), Poço Infinito e Oscilador Harmônico Simples. Para todos os casos utilizou-se uma condição inicial de um pacote gaussiano de desvio padrão para uma das componentes de , sendo a outra componente nula. O módulo quadrado do pacote gaussiano deve ter área unitária dentro da malha utilizada (de até ), por isso a constante de normalização deve ser .
Segue trecho do código comum a todos as simulações realizadas; a única diferença é que em um caso do OHS o pacote gaussiano é deslocado do meio da malha para a posição .
using Plots
using LaTeXStrings
using LinearAlgebra
using Integrals
function init(x, sigma)
arg1 = @. ((-(x-25)^2)/(2*sigma^2))
arg2 = 1/sqrt(sqrt(pi)*sigma)
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano
end
function OHS(V,x, k)
V = @. 0.5*k*(x-25)^2
return V
end
function poco(V, h)
#Quero colocar nas posições 18 e 32
V[round(Int64, 18/h)] = 100000
V[round(Int64, 32/h)] = 100000
return V
end
##Matrizes do método de Crank-Nicholson
function matriz(dt,h,L, V)
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.+1)))
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h)))
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V.-1)))
A = Array(A)
B = Array(B)
C = Array(C)
A_i = inv(A)
B_i = inv(B)
C_i = inv(C)
AiB = A_i*B
CiB = C_i*B
D = B_i*conj(A) + CiB
E = I(L) + C_i*conj(C)
F = B_i*A -CiB
G = A_i*conj(A) + I(L)
H = AiB + B_i*conj(C)
J = AiB - B_i*conj(C)
F_i = inv(F)
J_i = inv(J)
K = F_i*D
L = F_i*E
M = J_i*G
N = J_i*H
return K, L, M, N
end
function CN(size, h, tsize, V, dt, ci)
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1
g = zeros(Complex, tsize, size) ##phi 4
A, B, C, D = matriz(dt, h, size, V) #Matrizes do método Crank-Nicholson
f[1, :] = ci ##Condição Inicial
g[1, :] = zeros(size)
##Condições de Contorno
f[:, 1] = zeros(tsize)
f[:, end] = zeros(tsize)
g[:, 1] = zeros(tsize)
g[:, end] = zeros(tsize)
i=2 #Não interfiro nos contornos
while i<tsize
f[i, :] = A*f[i-1, :] - B*g[i-1, :]
g[i, :] = C*f[i-1, :] - D*g[i-1, :]
i+=1
end
return f, g
end
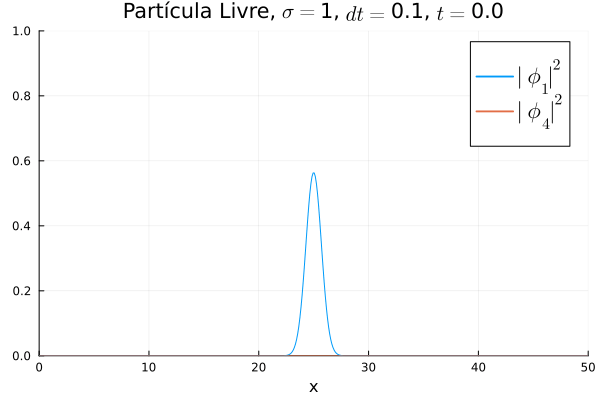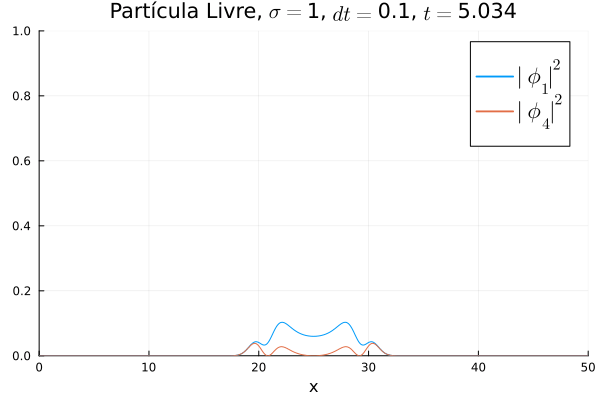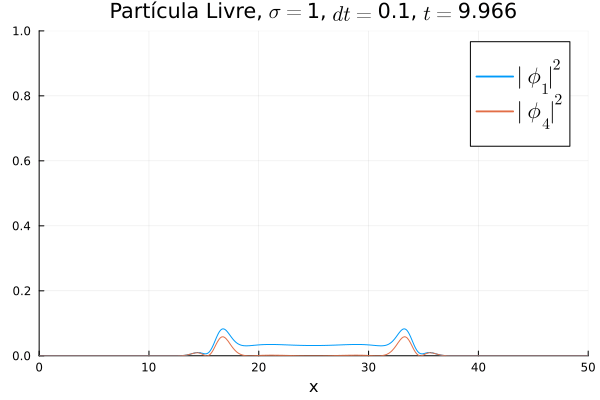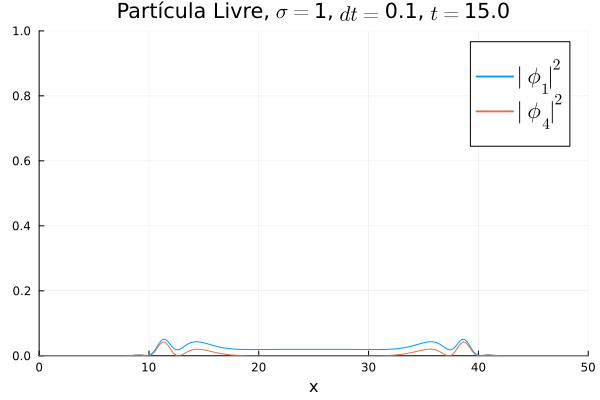
Partícula Livre
Aplicou-se o código demonstrado com potencial nulo para simular o caso da partícula livre. Segue abaixo código utilizado para gerar a animação:
Nota-se que mesmo que seja nula no início, a existência da partícula (neste caso, o elétron com spin up) gera a outra (pósitron com spin down). O comportamento é de dispersão, ou seja, a tendência é que a posição fique cada vez menos definida: a partícula livre, por estar fora da ação de um potencial, apresenta momento bem definido; pelo Princípio da Incerteza, a posição torna-se incerta. Nota-se também que as bordas estão longe o suficiente na escala de tempo utilizada, de maneira que as condições de contorno não afetam a simulação.
function main()
L = 50 #Dimensão espacial matriz
k=0.1 #"Constante Elástica" do oscilador harmônico
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 15
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
f,g =CN(size,h,tsize, V, dt,xi)
i=1
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15))
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15))
titulo = "Partícula Livre"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=1
end
arquivo = "diracfree.gif"
gif(anim, arquivo, fps=30)
end
main()
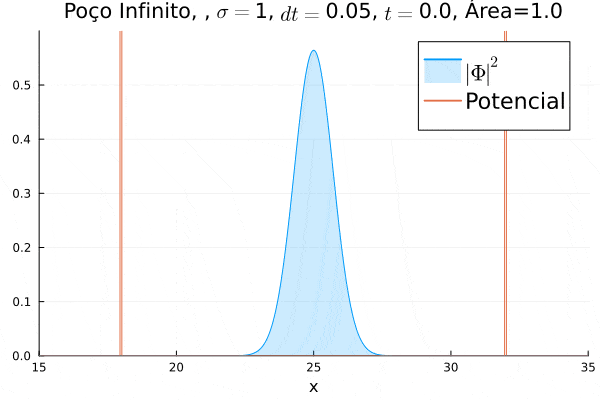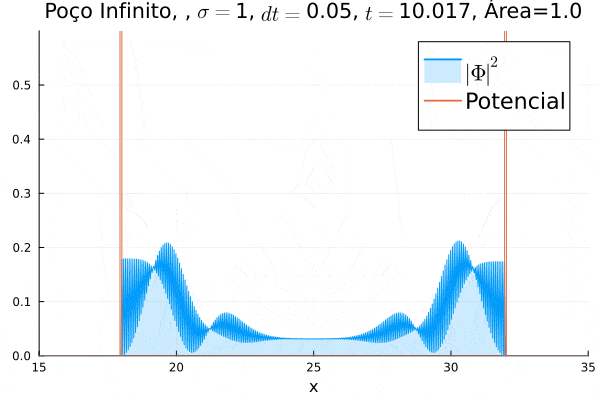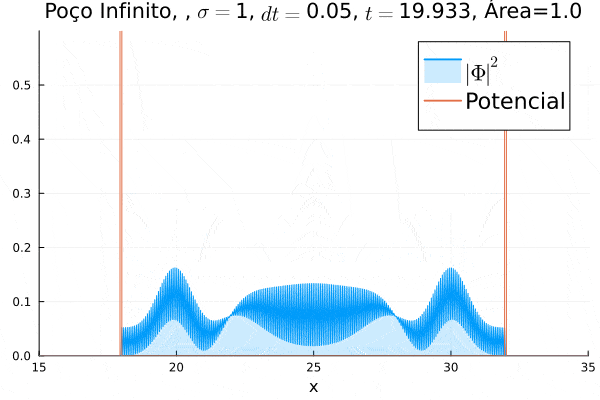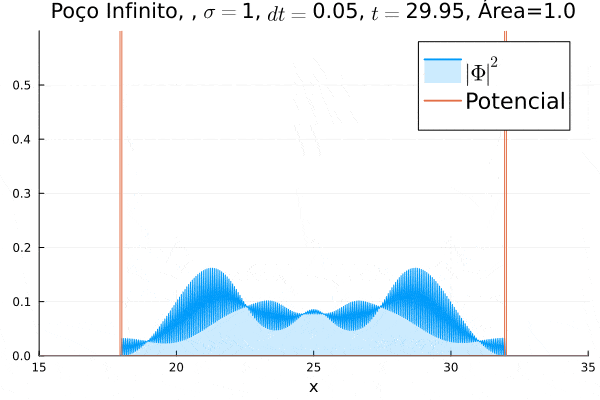
Poço Infinito
O poço infinito foi simulado colocando dois potenciais muito grandes em e . Abaixo está reproduzida a animação.
Nota-se que a função simulada é a soma dos quadrados dos módulos de cada função de onda (elétron e pósitron); é a integral de que deve sempre ser unitária, o que concorda com o obtido. Na animação é possível perceber um comportamento semelhante ao de uma onda estacionária, onde tem-se vários "harmônicos" associados ao pacote de ondas: como esperado, a função de onda é uma combinação linear dos autoestados do poço infinito.
Segue trecho do código utilizado para gerar a animação:
function main()
L = 50 #Dimensão espacial matriz
sigma = 1 #Largura do pacote gaussiano
dt = 0.05 #Passo temporal
size= 30*L #Utilizado para definir o passo espacial
h = L/size #Passo espacial
tmax = 30 #
tsize = round(Int64, tmax/dt) tamanho do vetor tempo.
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial de pacote gaussiano centralizado em x=25
#V = OHS(V,x,k)
V = poco(V, h) #Inicializa o potencial
f,g =CN(size,h,tsize, V, dt,xi) #Obtém as funções de onda e sua respectiva evolução temporal
##Produz-se a animação
i=1
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) #Resolve a integral em cada tempo, calculando a área e mostrando na animação
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3) #Arredonda.
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
titulo = "Poço Infinito"*", "*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,V, label="Potencial", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(15,35),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,0.6),
yticksfont=font(13),
)
i+=2 ##O passo é dado de 2 em 2 para deixar gif mais leve.
end
arquivo = "diracpoco.gif"
gif(anim, arquivo, fps=30)
end
main()
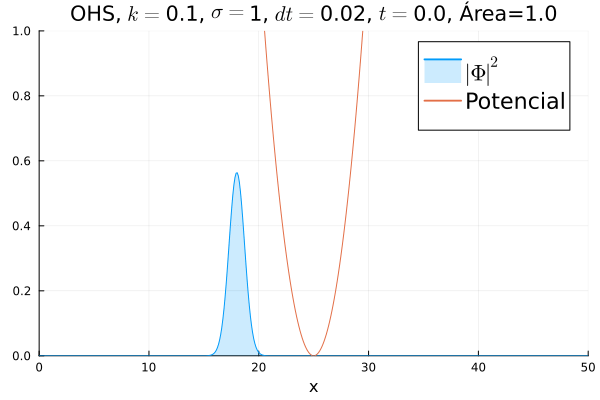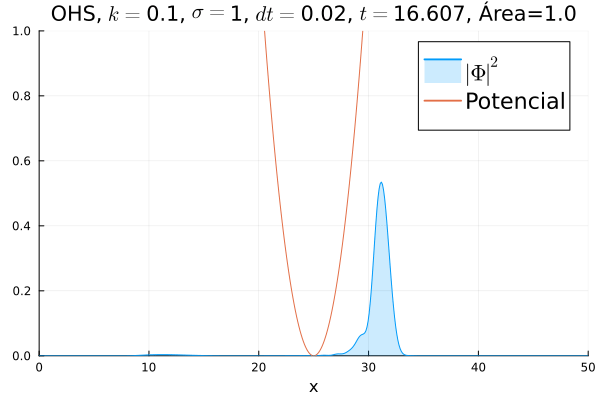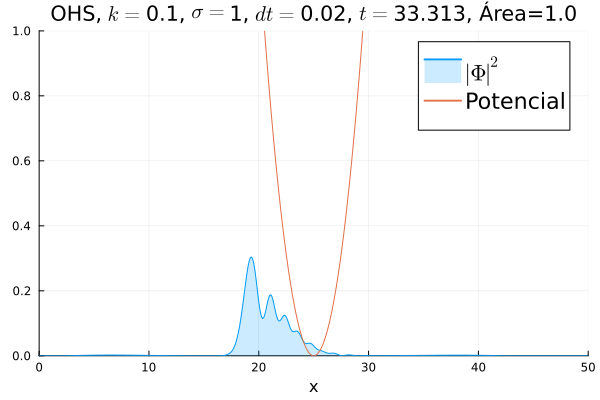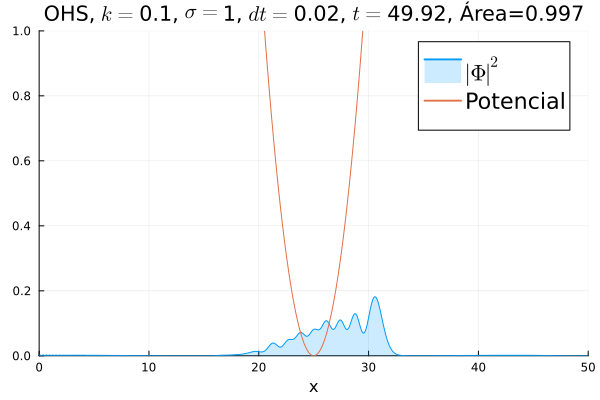
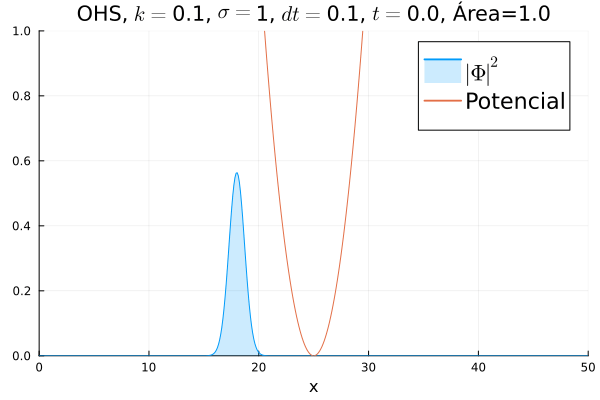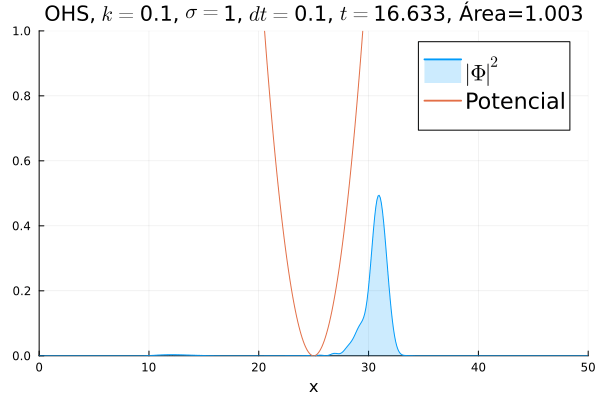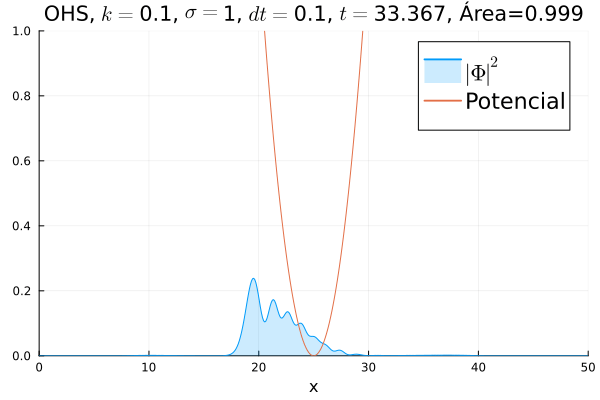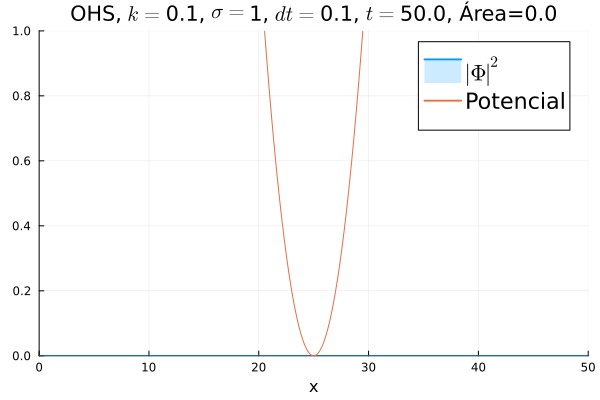
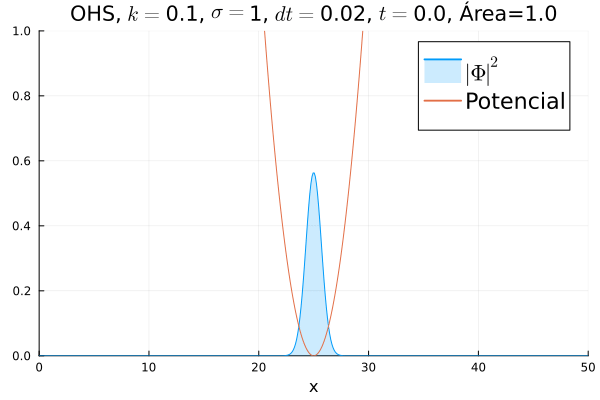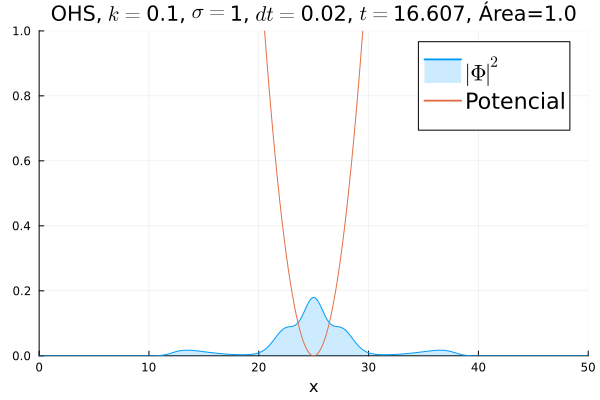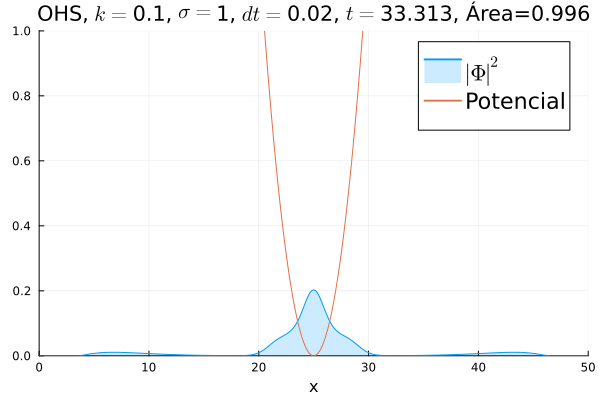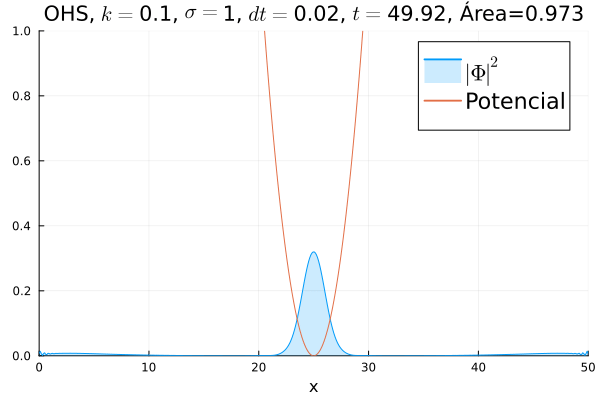
Oscilador Harmônico Simples
Inicialmente, realizou-se a simulação deslocando o pacote gaussiano para a posição inicial , com a finalidade de observar a oscilação. Testou-se a simulação com diferentes 's; escolheu-se o que está mostrado abaixo pois facilita a visualização do comportamento oscilatório.
Nota-se um comportamento análogo ao caso clássico; porém, em alguns momentos é possível observar certos harmônicos do pacote de onda. Além disso, nota-se nas extremidades um valor máximo para , também condizente com o caso clássico.
Durante testes nas simulações, notou-se que a área sob a curva possui variações quando se utiliza um passo muito alto. Nesse caso, a convergência do método de Crank-Nicolson para os valores teóricos depende da malha utilizada, embora a estabilidade dele seja incondicional. A diferença pode ser vista comparando-se a animação abaixo com a anterior:
Em seguida, passou-se para uma condição inicial com um pacote gaussiano centralizado:
Mesmo que a posição inicial esteja no centro, devido ao fato da posição não estar bem definida ocorrem pequenas oscilações em torno do ponto de equilíbrio.
Por fim, segue o código utilizado para o oscilador harmônico simples (a diferença entre cada caso é só as constantes e a condição inicial).
function main()
L = 50 #Dimensão espacial matriz
k=0.1 #"Constante Elástica" do oscilador harmônico
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 50
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
V = OHS(V,x,k) ##inicializa o potencial
f,g =CN(size,h,tsize, V, dt,xi)
i=1
#Faz o gif
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3)
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
#=
p=plot(x, probf, label=L"$|\phi_1|^2$", legendfont=font(15))
plot!(x, probg, label=L"$|\phi_4|^2$", legendfont=font(15))
=#
titulo = "OHS"*", "*L"$k=$"*string(k)*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,V, label="Potencial", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve
end
arquivo = "diracOHS.gif"
gif(anim, arquivo, fps=30)
end
main()
Equação 1D com potencial "escalar"
Por fim, consideraremos o problema com o potencial "escalar" . Dentro do formalismo da relatividade, os potenciais podem ser classificados de acordo com o seu comportamento frente a uma transformação de Poincaré: o potencial se transforma como um vetor (por isso chamado de potencial "vetor"), e o potencial , como um escalar (potencial "escalar"). Como exemplo de potencial do tipo vetor, temos os potenciais eletromagnéticos; e de potencial do tipo escalar, pode-se citar modelos de confinamento. Na prática, pode-se dizer que o potencial altera a massa de repouso "efetiva" da partícula. Para este assunto, deixamos (4) e (5) como referências.
Por ser um tópico bastante especializado, será considerado aqui apenas o caso do poço infinito. O problema é apenas uma extensão do que foi exposto nessa seção; a discretização e a estabilidade do método de Crank-Nicolson são análogas, bastando apenas fazer e .
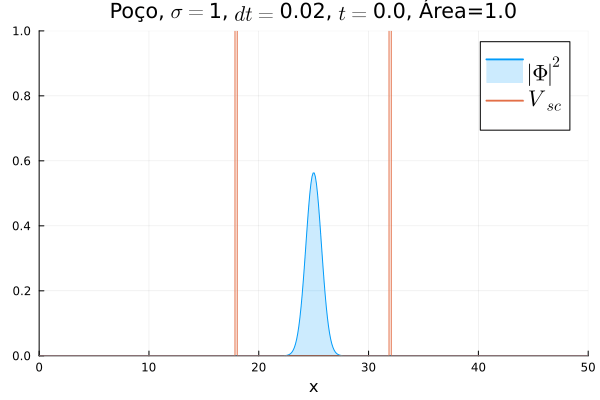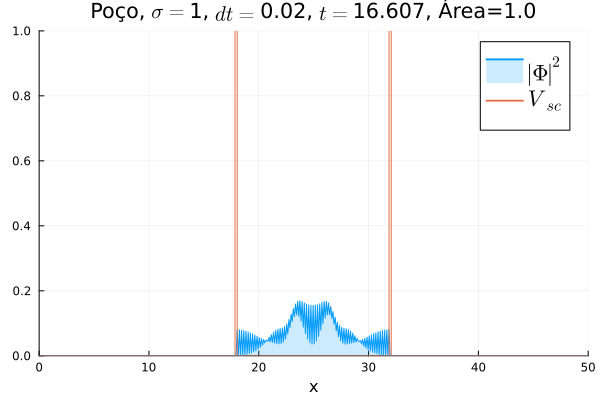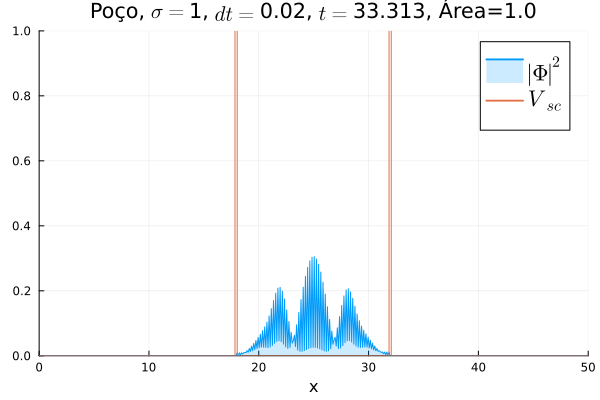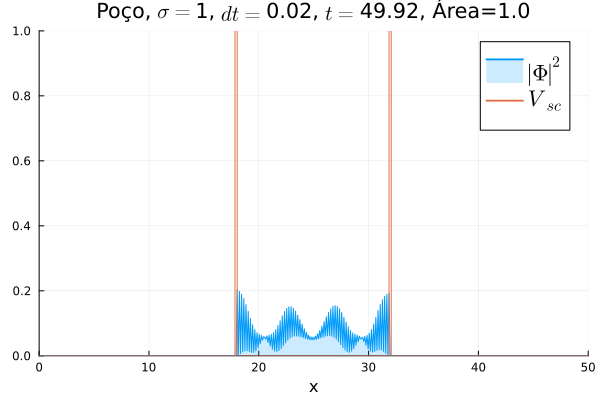
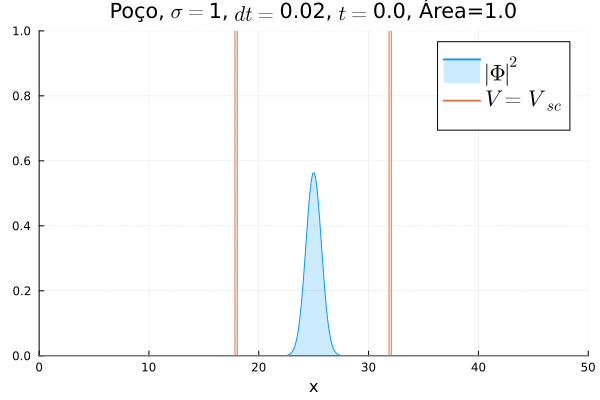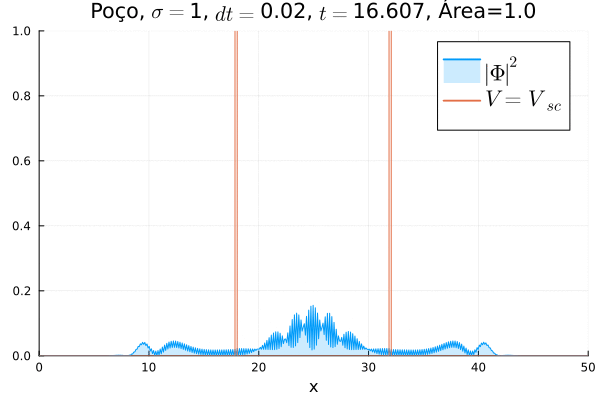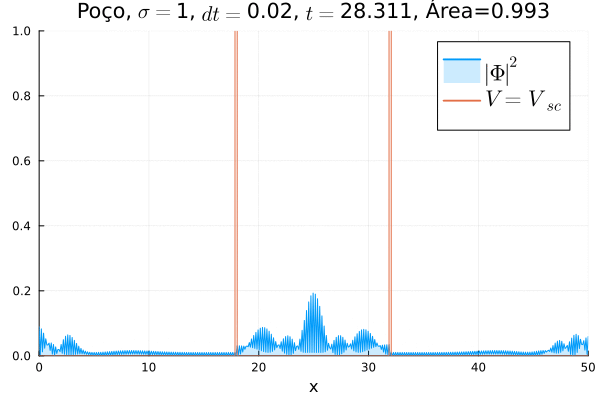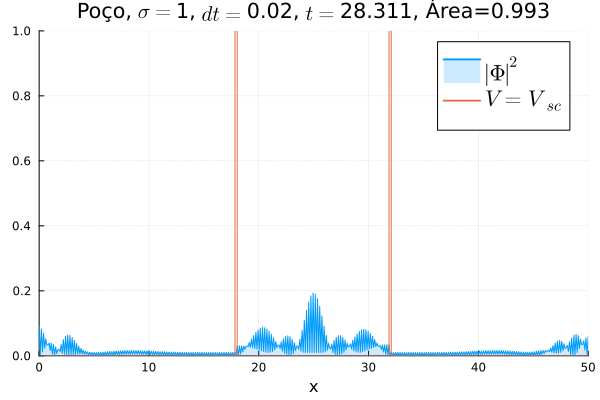
Poço Infinito
Fez-se uma simulação completamente análoga à anterior, mas usando e definindo o poço infinito em . A animação está reproduzida abaixo.
Não há diferença notável com relação ao poço infinito em : o confinamento da partícula não muda, mesmo que a sua massa de repouso "efetiva" sim. No entanto, ressalta-se que esse é o comportamento conjunto das duas componentes e ; o comportamento individual de cada uma pode ser diferente.
Em seguida, foi feita uma simulação colocando o poço infinito nos dois potenciais, ou seja, fazendo , conforme animação abaixo.
Dessa vez, o comportamento é bastante diferente: a partícula fica apenas parcialmente confinada no poço, sendo parte da função de onda transmitida. Assim, observa-se um fenômeno que não ocorre na formulação não relativística da Mecânica Quântica: o de tunelamento em uma barreira infinita.
Segue abaixo o código utilizado para produzir as animações, adaptado do código utilizado aqui. A diferença entre as duas animações é de apenas uma linha, definindo ou .
using Plots
using LaTeXStrings
using LinearAlgebra
using Integrals
function init(x, sigma)
arg1 = @. ((-(x-25)^2)/(2*sigma^2))
arg2 = 1/sqrt(sqrt(pi)*sigma)
return arg2*exp.(arg1) ##Inicializo com um pacote gaussiano
end
function poco(V, h)
#Quero colocar nas posições 18 e 32
V[round(Int64, 18/h)] = 100000
V[round(Int64, 32/h)] = 100000
return V
end
##Matrizes do método de Crank-Nicholson
function matriz(dt,h,L, V, Sc)
A = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V+Sc.+1)))
B = LinearAlgebra.Tridiagonal(ones(L-1).*(-dt/(4*h)), zeros(L), ones(L-1).*(dt/(4*h)))
C = Diagonal(ones(L).*(1 .+ im*dt*0.5.*(V-Sc.-1)))
A = Array(A)
B = Array(B)
C = Array(C)
A_i = inv(A)
B_i = inv(B)
C_i = inv(C)
AiB = A_i*B
CiB = C_i*B
D = B_i*conj(A) + CiB
E = I(L) + C_i*conj(C)
F = B_i*A -CiB
G = A_i*conj(A) + I(L)
H = AiB + B_i*conj(C)
J = AiB - B_i*conj(C)
F_i = inv(F)
J_i = inv(J)
K = F_i*D
L = F_i*E
M = J_i*G
N = J_i*H
return K, L, M, N
end
function CN(size, h, tsize, V, Sc, dt, ci)
f = zeros(Complex, tsize, size) #Cada linha representa vetor posição em um tempo diferente. ## phi 1
g = zeros(Complex, tsize, size) ##phi 4
A, B, C, D = matriz(dt, h, size, V, Sc) #Matrizes do método Crank-Nicholson
f[1, :] = ci ##Condição Inicial
g[1, :] = zeros(size)
##Condições de Contorno
f[:, 1] = zeros(tsize)
f[:, end] = zeros(tsize)
g[:, 1] = zeros(tsize)
g[:, end] = zeros(tsize)
i=2 #Não interfiro nos contornos
while i<tsize
f[i, :] = A*f[i-1, :] - B*g[i-1, :]
g[i, :] = C*f[i-1, :] - D*g[i-1, :]
i+=1
end
return f, g
end
function main()
L = 50 #Dimensão espacial matriz
sigma = 1 #Largura do pacote gaussiano
dt = 0.02
size= 10*L
h = L/size ##Passo espacial
tmax = 50
tsize = round(Int64, tmax/dt) #Tamanho do vetor tempo
t = LinRange(0, tmax, tsize)
x = LinRange(0, L, size)
V = zeros(size)
Sc = copy(V)
xi = init(LinRange(0, L, size), sigma) #Condição inicial pacote gaussiano
Sc = poco(Sc,h) ##potencial "escalar"
V = copy(Sc) ##potencial "vetor"
f,g = CN(size,h,tsize,V,Sc,dt,xi)
i=1
#Faz o gif
anim = @animate while i<=tsize
f_real = real(f[i, :])
f_imag = imag(f[i, :])
g_real = real(g[i, :])
g_imag = imag(g[i, :])
probf = abs2.(f[i, :])
probg = abs2.(g[i, :])
prob = probf + probg
problem = SampledIntegralProblem(prob, x) ##Calcula a área sob a curva
method = TrapezoidalRule()
integral = solve(problem, method)
integral = round(integral[1]; digits=3)
integral = string(integral)
p = plot(x, prob,label=L"$|\Phi|^2$", legendfont=font(15), fill=true, fillalpha=0.2)
titulo = "Poço"*", "*L"$\sigma=$"*string(sigma)*", "* L"$dt=$"*string(dt)* ", " *L"$t=$" * string(round(t[i], digits=3))*", Área="*integral
plot!(x,Sc, label=L"$V=V_{sc}$", legendfont=font(15))
plot!(title=titulo,
xlabel = "x",
xlim=(0,50),
xticksfont = font(13),
ticksfontsize = 10,
ylim=(0,1),
yticksfont=font(13),
)
i+=5 ##Feito de 5 em 5 para deixar .gif mais leve
end
arquivo = "diracVscVPoco.gif"
gif(anim, arquivo, fps=30)
end
main()
Equação 2D
Utilizou-se o método de Leap-Frog para simulação da equação de Dirac bidimensional em um potencial Coulombiano central e em um potencial cossenoide. Em ambos casos, o potencial não depende do tempo e a condição inicial constituiu-se de um pacote gaussiano, centralizado em para e em para . De forma aproximada, atribuiu-se para o passo temporal seguinte:
Segue abaixo o código utilizado para ambos potenciais, o qual seu uso difere apenas em qual potencial foi comentado:
using Plots
using LinearAlgebra
function initial_values()
L=10 #Malha de 4*(L/h)² de -L a L nas duas dimensões
h=1/16 #dx,dy=h
dt=0.01
ep=0.8 #0<ep<=1 -> := v/c
x=LinRange(-L,L,2*Int(L/h))
y=LinRange(-L,L,2*Int(L/h))
#Potencial Coulombiano
V= zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
Qe=1.
K=1 #K=9*10^9
V = [ -K*Qe/sqrt((x[i]^2 + y[j]^2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#Potencial Cossenoide
#V = [ cos((-4*pi/sqrt(3))*x[i])+cos((2*pi/sqrt(3))*x[i]+2*pi*y[j])+cos((2*pi/sqrt(3))*x[i]-2*pi*y[j]) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#psi 1 inicial (t=0)
psi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
psi1 = [ (exp(-((x[i])^2+(y[j])^2)/2)) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#psi4 iniciall (t=0)
psi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
psi4 = [ exp(-((x[i] -1 )^2+(y[j] -1)^2)/2) for i in 1:2*Int(L/h), j in 1:2*Int(L/h) ]
#próximo psi1 (t=0+dt)
nextpsi1 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
j=2
while j < 2*Int(L/h)
i=2
while i < 2*Int(L/h)
nextpsi1[i,j] = psi1[i,j]-sin(dt/ep)*((psi4[i+1,j]-psi4[i-1,j]) + (psi4[i,j+1]-psi4[i,j-1]))/(2*h)-im*(-im*sin(dt/(ep^2))*psi4[i,j]+h*V[i,j]*psi1[i,j])
i+=1
end
j+=1
end
#próximo psi4 (t=0+dt)
nextpsi4 =zeros(ComplexF64,2*Int(L/h),2*Int(L/h))
j=2
while j < 2*Int(L/h)
i=2
while i < 2*Int(L/h)
nextpsi4[i,j]= psi4[i,j]-sin(dt/ep)*((psi1[i+1,j]-psi1[i-1,j]) + (psi1[i,j+1]-psi1[i,j-1]))/(2*h)-im*(im*sin(dt/(ep^2))*psi1[i,j]+h*V[i,j]*psi4[i,j])
i+=1
end
j+=1
end
return L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4
end
L,h,dt,ep,x,y,V,psi1,psi4,nextpsi1,nextpsi4=initial_values()
#listas para salvar os frames do gif
anim_psi1=[]
anim_psi4=[]
#cópia para manipulação
uu=deepcopy(psi1)
vv=deepcopy(psi4)
t=0; tmax=5
while t < tmax
global j
global uu; global vv;
global u; global v;
u=deepcopy(nextpsi1)
v=deepcopy(nextpsi4)
j=2
while j < 2*Int(L/h)
global i=2
while i < 2*Int(L/h)
global i
nextpsi1[i,j]= -(dt/(ep*h))*(v[i+1,j]-v[i-1,j])+((im*dt)/(ep*h))*(v[i,j+1]-v[i,j-1])-((2*im*dt)/(ep^2))*u[i,j]-(2*dt*im)*V[i,j]*u[i,j]+uu[i,j]
nextpsi4[i,j]= -(dt/(ep*h))*(u[i+1,j]-u[i-1,j])-((im*dt)/(ep*h))*(u[i,j+1]-u[i,j-1])+((2*im*dt)/(ep^2))*v[i,j]+(2*dt*im)*V[i,j]*v[i,j]+vv[i,j]
i+=1
end
j+=1
end
uu=deepcopy(u)
vv=deepcopy(v)
global t+=dt
push!(anim_psi1,deepcopy(nextpsi1))
push!(anim_psi4,deepcopy(nextpsi4))
end
using LaTeXStrings
using Printf
#montagem do gif
function psi_anim(x,y,psi,tmax)
i=1
anim = @animate while i<=length(psi)
psi_real = real.(psi[i])
psi_imag = imag.(psi[i])
prob = abs2.(psi[i])
t=0.01*i
titulo="Potencial Coulombiano, "*L"| \Phi |^{2}"*@sprintf("em t=%0.2f",t)
#titulo=@sprintf("| \Phi |^{2}em t = %f",
u=2*L/h #exibe a malha de forma reduzida
p = surface(x[Int(u/4):Int(3*u/4)],y[Int(u/4):Int(3*u/4)],prob[Int(u/4):Int(3*u/4),Int(u/4):Int(3*u/4)],title=titulo, xlabel = "x",ylabel="y",zlabel="Densidade de Probabilidade" ,zlim=(-1,1),clim=(0, maximum(psi_real)))
i+=1
end
arquivo = "dirac2D.gif"
gif(anim, arquivo, fps=30)
end
psi_anim(x,y,anim_psi1,tmax)
Potencial Coulombiano
Na animação gerada, nota-se o padrão de dispersão para o infinito, pois o potencial escolhido varia de positivamente no caso escolhido. Observa-se um padrão de ruído na parte central, o qual não foi estudado afundo, mas é exclusivo de pontos próximos à um ponto de divergência da função potencial.
Potencial Cossenoide
Reproduziu-se o potencial estudado para representações do grafeno em um único plano. Observa-se, no período de tempo exibido, que padrões de ruído não são encontrados e a tendência para o infinito permanece.
Referências
- The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928.
- SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012.
- BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017.
- SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973.
- THALLER, B. The Dirac equation. Berlin: Springer, 2010.




































![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi =H\Psi \to \left[iI_{4}{\frac {\partial }{\partial t}}-H\right]\Psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a47cd71f320c16b7c19d774e965a50d7a9ffe74c)







![{\displaystyle i\partial _{t}\mathbf {\Phi } =[-i\sigma _{1}\partial _{x}+\sigma _{3}]\mathbf {\Phi } +[V(t,x)I_{2}]\mathbf {\Phi } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/856d45f8bb00f22f263d8cb7b4beaa0994aca01b)

















![{\displaystyle i\delta _{t}\mathbf {\Phi _{j}^{n}} =[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/066376632627056eca4aa2be571668af4d36d9ae)
![{\displaystyle i{\frac {\mathbf {\Phi _{j}^{n+1}} -\mathbf {\Phi _{j}^{n}} }{\Delta t}}=[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7446ce3f82727c2b53fa903abb6796149e3ae1b4)
![{\displaystyle i\mathbf {\Phi _{j}^{n+1}} =\mathbf {\Phi _{j}^{n}} +\Delta t[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n}} +\Delta t[V_{j}^{n}I_{2}]\mathbf {\Phi _{j}^{n}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7fbc7e09a9758938eb89013fe5030a54e5abc1)




![{\displaystyle i\mathbf {\Phi _{j}^{n+1}} =\mathbf {\Phi _{j}^{n}} +\Delta t[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n+1}} +\Delta t[V_{j}^{n+1}I_{2}]\mathbf {\Phi _{j}^{n+1}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/315ca5c2ae8c8d289445d2fad96a783defa76791)



![{\displaystyle i\delta _{t}\mathbf {\Phi _{j}^{n}} =[-i\sigma _{1}\delta _{x}+\sigma _{3}]\mathbf {\Phi _{j}^{n+1/2}} +[V_{j}^{n+1/2}I_{2}]\mathbf {\Phi _{j}^{n+1/2}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e9be8f4009379093880a6419a1bfc7236ab22d)


![{\displaystyle i{\frac {\mathbf {\Phi _{j}^{n+1}} -\mathbf {\Phi _{j}^{n}} }{\Delta t}}=-{\frac {i}{2}}\sigma _{1}\left[{\frac {\mathbf {\Phi _{j+1}^{n+1}} -\mathbf {\Phi _{j-1}^{n+1}} }{2h}}+{\frac {\mathbf {\Phi _{j+1}^{n}} -\mathbf {\Phi _{j-1}^{n}} }{2h}}\right]+\sigma _{3}\left({\frac {\mathbf {\Phi _{j}^{n+1}} +\mathbf {\Phi _{j}^{n}} }{2}}\right)+I_{2}\left({\frac {V_{j}^{n+1}\mathbf {\Phi _{j}^{n+1}} +V_{j}^{n}\mathbf {\Phi _{j}^{n}} }{2}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36c63cac7e0404678553d9417eff8e3740d63a6e)
![{\displaystyle \left[I_{2}+{\frac {i}{2}}\Delta t\sigma _{3}+{\frac {i}{2}}\Delta tV_{j}^{n+1}I_{2}\right]\mathbf {\Phi _{j}^{n+1}} +{\frac {\Delta t}{4h}}\sigma _{1}\left[\mathbf {\Phi _{j+1}^{n+1}} -\mathbf {\Phi _{j-1}^{n+1}} \right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11db4df7b507157a75b89ad679b87003f3ef6857)
![{\displaystyle \left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}\right]\mathbf {\Phi _{j}^{n}} -{\frac {\Delta t}{4h}}\sigma _{1}\left[\mathbf {\Phi _{j+1}^{n}} -\mathbf {\Phi _{j-1}^{n}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8730f3d4a62979df98a9dba9c63c334ea822a579)





![{\displaystyle {\begin{cases}\left[1+{\frac {i\Delta t}{2}}(V_{j}^{n+1}+1)\right]f_{j}^{n+1}+{\frac {\Delta t}{4h}}(g_{j+1}^{n+1}-g_{j-1}^{n+1})=\left[1-{\frac {i\Delta t}{2}}(V_{j}^{n}+1)\right]f_{j}^{n}-{\frac {\Delta t}{4h}}(g_{j+1}^{n}-g_{j-1}^{n})\\\left[1+{\frac {i\Delta t}{2}}(V_{j}^{n+1}-1)\right]g_{j}^{n+1}+{\frac {\Delta t}{4h}}(f_{j+1}^{n+1}-f_{j-1}^{n+1})=\left[1-{\frac {i\Delta t}{2}}(V_{j}^{n}-1)\right]g_{j}^{n}-{\frac {\Delta t}{4h}}(f_{j+1}^{n}-f_{j-1}^{n})\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/124cc692a9582c970eb9016ec040d79fadb3e1cc)

















![{\displaystyle \left[I_{2}+{\frac {i}{2}}\Delta t\sigma _{3}+{\frac {i}{2}}\Delta tV_{j}^{n+1}I_{2}\right]\mathbf {A} ^{n+1}e^{ikqjh}+{\frac {\Delta t}{4h}}\sigma _{1}\mathbf {A} ^{n+1}\left[e^{ikq(j+1)h}-e^{ikq(j-1)h}\right]=\left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}\right]\mathbf {A} ^{n}e^{ikqjh}-{\frac {\Delta t}{4h}}\sigma _{1}\mathbf {A} ^{n}\left[e^{ikq(j+1)h}-e^{ikq(j-1)h}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/063cae16464b2521ffda10233f3979d7764b70d5)


![{\displaystyle \left[I_{2}+{\frac {i}{2}}\Delta t\sigma _{3}+{\frac {i}{2}}\Delta tV_{j}^{n+1}I_{2}+{\frac {\Delta t}{4h}}\sigma _{1}\left(e^{ikqh}-e^{-ikqh}\right)\right]\mathbf {A} ^{n+1}=\left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}-{\frac {\Delta t}{4h}}\sigma _{1}\left(e^{ikqh}-e^{-ikqh}\right)\right]\mathbf {A} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f4ee31dc98c2753dcd52ea1f72ab9fe542b4d6b)
![{\displaystyle \left[I_{2}+{\frac {i}{2}}\Delta t\sigma _{3}+{\frac {i}{2}}\Delta tV_{j}^{n+1}I_{2}+{\frac {\Delta t}{4h}}\sigma _{1}\left({\frac {\sin(kqh)}{2i}}\right)\right]\mathbf {A} ^{n+1}=\left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}-{\frac {\Delta t}{4h}}\sigma _{1}\left({\frac {\sin(kqh)}{2i}}\right)\right]\mathbf {A} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91045c135ca2637beee0fccb3f8f26dc4d4f39cd)
![{\displaystyle \left[I_{2}+{\frac {i}{2}}\Delta t\sigma _{3}+{\frac {i}{2}}\Delta tV_{j}^{n+1}I_{2}-{\frac {i\Delta t}{4h}}\sigma _{1}\left({\frac {\sin(kqh)}{2}}\right)\right]\mathbf {A} ^{n+1}=\left[I_{2}-{\frac {i}{2}}\Delta t\sigma _{3}-{\frac {i}{2}}\Delta tV_{j}^{n}I_{2}+{\frac {i\Delta t}{4h}}\sigma _{1}\left({\frac {\sin(kqh)}{2}}\right)\right]\mathbf {A} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5bcc4e503cf1206d9c6d92fcb89bd4b39fe7db0)






![{\displaystyle i\partial _{t}\mathbf {\Phi } =[-{\frac {i}{\varepsilon }}(\sigma _{1}\partial _{x}+\sigma _{2}\partial _{y})+{\frac {1}{\varepsilon ^{2}}}\sigma _{3}]\mathbf {\Phi } +[V(t,x)I_{2}]\mathbf {\Phi } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4393e415a2d3191ddc97ed348165c49bf9f0a47c)
![{\displaystyle i\partial _{t}\mathbf {\Phi } _{i,j}^{n}=[-{\frac {i}{\varepsilon }}(\sigma _{1}\partial _{x}+\sigma _{2}\partial _{y})+{\frac {1}{\varepsilon ^{2}}}\sigma _{3}]\mathbf {\Phi } _{i,j}^{n}+[V(t,x)I_{2}]\mathbf {\Phi } _{i,j}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7438cc6b4e49dc86c26802758240da30ed75dbf)





![{\displaystyle {\Phi _{1}}_{i,j}^{n+1}=-{\frac {\Delta t}{h\varepsilon }}[({\Phi _{4}}_{i+1,j}^{n}-{\Phi _{4}}_{i-1,j}^{n})-i({\Phi _{4}}_{i,j+1}^{n}-{\Phi _{4}}_{i,j-1}^{n})]-2i\Delta t[{\frac {1}{\varepsilon ^{2}}}+V_{i,j}^{n}]{\Phi _{1}}_{i,j}^{n}+{\Phi _{1}}_{i,j}^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f818c9097df578e1ec825bf2a5d23169102d143f)
![{\displaystyle {\Phi _{4}}_{i,j}^{n+1}=-{\frac {\Delta t}{h\varepsilon }}[({\Phi _{1}}_{i+1,j}^{n}-{\Phi _{1}}_{i-1,j}^{n})+i({\Phi _{1}}_{i,j+1}^{n}-{\Phi _{1}}_{i,j-1}^{n})]+2i\Delta t[{\frac {1}{\varepsilon ^{2}}}+V_{i,j}^{n}]{\Phi _{4}}_{i,j}^{n}+{\Phi _{4}}_{i,j}^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d674c62c150c291979e5b3b724e255b12766ac93)