Equação de Burgers
Grupo: Eduardo Pedroso, Luis Gustavo Lang Gaiato, William...
Um dos maiores desafios no campo dos sistemas complexos é a compreensão do fenômeno de turbulência. Simulações computacionais contribuíram bastante para o entendimento dessa área, no entanto, ainda não existe nenhuma teoria que explique com sucesso esse comportamento e permita prever outros importantes fenômenos como misturas, convecção e combustão turbulentas, com base nas equações fundamentais da dinâmica de fluidos. Isso se deve ao fato de que a equação para os fluidos mais simples (incompressíveis) já deve levar em consideração propriedades não lineares [1]. Da equação de Navier–Stokes:
Devido à incompressibilidade, a pressão é definida pela equação de Poisson:
Em 1939 o cientista alemão Johannes Martinus Burgers simplificou a equação de Navier-Stokes, removendo o termo de pressão. A equação ficou conhecida como equação de Burgers. Em uma dimensão, onde corresponde ao campo de velocidades e ao coeficiente de difusão:
A equação de Burgers é não linear e, portanto, espera-se um comportamento similar ao da turbulência. No entanto, foi demonstrado posteriormente que a equação de Burgers homogênea, não possuí a propriedade mais importante atribuída ao fenômeno de turbulência: o comportamento caótico em relação à pequenas mudanças nas condições iniciais. Utilizando a transformação de Hopf-Cole, que transforma a equação de Burgers em uma equação parabólica linear é possível observar essa característica [2].
Do ponto de vista numérico, isso é bastante importante, pois permite a comparação das soluções da equação não linear numérica com o resultado analítico. Dessa forma, pode-se investigar a qualidade do método numérico utilizado.
Modelo de Deposição - Crescimento de Interfaces
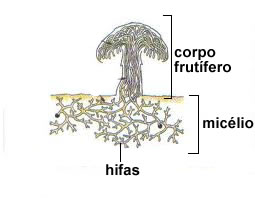
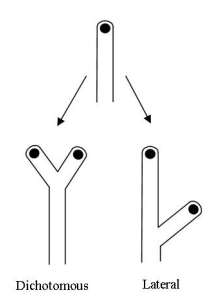
Um exemplo de aplicação é no crescimento de interfaces por deposição, já que a equação de Burgers é equivalente a equação conhecida como, equação de Kardar-Parisi-Zhang (equação KPZ), um modelo de crescimento de uma superfície sólida por deposição de vapor (ou erosão de material de uma superfície sólida), que mostra a evolução da altura da camada com o tempo [5].
A equação é obtida a partir da equação de advecção simples para uma superfície se movimentando com velocidade :
A velocidade é assumida como sendo proporcional ao gradiente de (superfície evolui na direção do gradiente). A difusão da superfície é descrita pelo termo de difusão.
A equação de Burgers é obtida a partir da equação KPZ, pelo gradiente de
- ↑ F. M. White, Viscous Fluid Flow, 3rd ed. New York, NY: McGraw-Hill Professional, 2005.
- ↑ Hopf, E. (1950). The partial differential equation ut + uux = μxx. Communications on Pure and Applied Mathematics, 3(3), 201–230. doi:10.1002/cpa.3160030302
- ↑ P. L. Moraes. Fungos. Mundo Educação. Disponível em: https://mundoeducacao.uol.com.br/biologia/os-fungos.htm. Acesso em: 15 de Maio de 2021.
- ↑ Erro de citação: Marca
<ref>inválida; não foi fornecido texto para as refs chamadasHOPKINS - ↑ REIS, F. D. A. A. Depinning transitions in interface growth models. Brazilian journal of physics, v. 33, n. 3, p. 501–513, 2003













