Difusão ambipolar em plasmas: mudanças entre as edições
Sem resumo de edição |
|||
| (28 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
== Equação da difusão ambipolar == | == Equação da difusão ambipolar == | ||
Esse trabalho tem como objetivo demonstrar uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma(gás formado de elétrons e íons). A difusão é o modo como um fluido se dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. | Esse trabalho tem como objetivo demonstrar uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma(gás formado de elétrons e íons). A difusão é o modo como um fluido se dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. | ||
| Linha 22: | Linha 23: | ||
<math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> , | <math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> , | ||
onde <math>u^2 = \nu_a D_a</math> e <math>\alpha = 1/D_a</math>, sendo <math>\nu_a</math> a frequência de colisão ambipolar e <math>D_a</math> o coeficiente de difusão ambipolar, que é calculado através de uma media dos coeficientes de difusão dos elétrons e íons. | onde <math>u^2 = \nu_a D_a</math> e <math>\alpha = 1/D_a</math>, sendo <math>\nu_a</math> a frequências de colisão dos íons e elétrons nas patículas neutras, chamada frequência de colisão ambipolar e <math>D_a</math> o coeficiente de difusão ambipolar, que é calculado através de uma media dos coeficientes de difusão dos elétrons e íons. | ||
Como tratamos do caso unidimensional, a equação 1 torna-se | |||
<math>\frac{1}{ | <math>\frac{\partial^2 n(x,t)}{\partial x^2} = \frac{1}{u^2} \frac{\partial^2 n(x,t)}{\partial t^2} + \alpha \frac{\partial n(x,t)}{\partial t} \qquad (2)</math> . | ||
== Aproximações == | |||
As eq.(3) e (4) são termos da eq.(1), onde foram feitas algumas aproximações, produzido pelo livro do J.A Bittencourt <ref name=Simony+Cahn64> Fundamentals of plama physics/J.A Bittencourt - 3rd ed. </ref> | |||
<math>\frac{\partial n(\vec r,t)}{\partial t} \approx \frac{n(\vec r,t)}{\tau^2} \qquad (3)</math> | |||
<math> | <math>\frac{1}{\nu_a} \frac{\partial^2 n(\vec r,t)}{\partial t^2} \approx \frac{n(\vec r,t)}{\nu_a \tau^2} \qquad (4)</math> | ||
Comparando as eq.(3) e (4),obtemos: <math>\tau = 1/\nu_a</math>. Observe que se <math>\nu_a \tau</math> >> 1, isto é, se os elétrons ou íons tem muitas colisões com partículas neutras durante o tempo característico para difusão <math>\tau</math>. Então o termo que carrega <math>u^2</math> na eq. (1) pode ser negligenciado. Como consequência durante todo tempo a concentração de elétrons e íons são iguais: <math>n_e = n_i = n</math>, assim, a eq.(1) se reduz a seguinte equação de difusão: | |||
<math>\ | <math>D_a\nabla^2 n(\vec r,t) = \frac{\partial n(\vec r,t)}{\partial t} \qquad (5)</math> | ||
== O Método == | == O Método == | ||
| Linha 48: | Linha 49: | ||
damped wave equation", viXra, 2016 </ref>. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional | damped wave equation", viXra, 2016 </ref>. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional | ||
<math> \frac{\partial^2 n(x,t)}{\partial t^2} + 2h \frac{\partial n(x,t)}{\partial t} = c^2 \frac{\partial^2 n(x,t)}{\partial x^2} \qquad ( | <math> \frac{\partial^2 n(x,t)}{\partial t^2} + 2h \frac{\partial n(x,t)}{\partial t} = c^2 \frac{\partial^2 n(x,t)}{\partial x^2} \qquad (6) </math>. | ||
| Linha 62: | Linha 63: | ||
<math> \frac{\partial^2 n}{\partial t^2} |_i^k = \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^2 n}{\partial t^4}|_i^k + O(\Delta t^4) </math> , | <math> \frac{\partial^2 n}{\partial t^2}|_i^k = \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^2 n}{\partial t^4}|_i^k + O(\Delta t^4) </math> , | ||
<math> \frac{\partial n}{\partial t} |_i^k = \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4) </math> , | <math> \frac{\partial n}{\partial t} |_i^k = \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4) </math> , | ||
| Linha 68: | Linha 69: | ||
<math> \frac{\partial^2 n}{\partial x^2} |_i^k = \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^2 n}{\partial x^4}|_i^k + O(\Delta x^4) </math>. | <math> \frac{\partial^2 n}{\partial x^2} |_i^k = \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^2 n}{\partial x^4}|_i^k + O(\Delta x^4) </math>. | ||
Substituindo essas relações na equação | Substituindo essas relações na equação 6, obtemos: | ||
<math> \left[ \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k + O(\Delta t^4)\right] + 2h\left[ \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4)\right] = c^2\left[ \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O(\Delta x^4)\right] </math>. | <math> \left[ \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k + O(\Delta t^4)\right] + 2h\left[ \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4)\right] = c^2\left[ \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O(\Delta x^4)\right] </math>. | ||
Omitindo todos os temos de ordem <math>O\{\Delta t^2,\Delta x^2\}</math> e isolando <math> | Omitindo todos os temos de ordem <math>O\{\Delta t^2,\Delta x^2\}</math> e isolando <math>n_i^{k_1}</math>, obtemos | ||
<math> | <math> n_i^{k+1} = \frac{1}{1 + h\Delta t}[2(1-s)n_i^k - (1 - h\Delta t)n_i^{k-1} + s(n_{i+1}^k + n_{i-1}^k)] \qquad (7) </math> , | ||
sendo <math> s = (c^2\Delta t^2/\Delta x^2) </math>. | sendo <math> s = (c^2\Delta t^2/\Delta x^2) </math>. | ||
Essa é a equação para resolver o problema para <math>k \geq 1</math>, porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar <math> | Essa é a equação para resolver o problema para <math>k \geq 1</math>, porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar <math>n_i^1</math> a paritr de <math>n_i^0</math>, para então calcular os demais passos. Para isso assumimos que a função é inicialmente estacionária e fazemos | ||
<math>n_t(x,0) = 0 \Rightarrow \frac{n_i^1 - n_i^{-1}}{\Delta t} = 0 \Rightarrow n_i^1 = n_i^{-1}</math> | <math>n_t(x,0) = 0 \Rightarrow \frac{n_i^1 - n_i^{-1}}{\Delta t} = 0 \Rightarrow n_i^1 = n_i^{-1}</math> [https://vixra.org/pdf/1601.0341v1.pdf] | ||
Substituindo na equação | Substituindo na equação 7 para <math>k = 0</math> obtemos | ||
<math> n_i^1 = \frac{1}{2}[2(1-s)n_i^0 + s(n_{i+1}^0 + n_{i-1}^0)] \qquad ( | <math> n_i^1 = \frac{1}{2}[2(1-s)n_i^0 + s(n_{i+1}^0 + n_{i-1}^0)] \qquad (8) </math>. | ||
Com as equações | Com as equações 7 e 8, e tomando as devidas condições de contorno nas bordas (no caso desse trabalho usamos bordas fixas em 0 e também condições periódicas de contorno), podemos calcular a evolução temporal da função de densidade. Esse método é estável para <math>0 \leq s \leq 1</math> e seu erro é | ||
<math> E\{n_i^k\} = - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k - \frac{h\Delta t^2}{3}\frac{\partial^3 n}{\partial t^3}|_i^k + c^2\frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O\{\Delta t^4, \Delta x^4\} </math>. | <math> E\{n_i^k\} = - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k - \frac{h\Delta t^2}{3}\frac{\partial^3 n}{\partial t^3}|_i^k + c^2\frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O\{\Delta t^4, \Delta x^4\} </math>. | ||
| Linha 98: | Linha 99: | ||
Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura <math>L=10</math>. Fizemos o plasma inicialmente concentrado na região central do tubo: <math>n(x,0)=1</math> para <math>L/4 \leq x \leq 3L/4</math> e <math>n(x,0)=0</math> para <math>x</math> fora dessa região. Usamos <math>\Delta x = 0.1</math> e <math>\Delta t = 0.01</math>, que resulta em <math>s = 0.01\nu_aD_a</math>, e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de <math>\nu_i</math> e <math>D_a</math>. Para garantir a estabilidade do método, essas constantes devem ser tais que <math> 0 \leq \nu_iD_a \leq (\Delta x / \Delta t)^2</math>. | Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura <math>L=10</math>. Fizemos o plasma inicialmente concentrado na região central do tubo: <math>n(x,0)=1</math> para <math>L/4 \leq x \leq 3L/4</math> e <math>n(x,0)=0</math> para <math>x</math> fora dessa região. Usamos <math>\Delta x = 0.1</math> e <math>\Delta t = 0.01</math>, que resulta em <math>s = 0.01\nu_aD_a</math>, e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de <math>\nu_i</math> e <math>D_a</math>. Para garantir a estabilidade do método, essas constantes devem ser tais que <math> 0 \leq \nu_iD_a \leq (\Delta x / \Delta t)^2</math>. | ||
Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 (<math>n(0,t) = n(L,t) = 0</math>) e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto | Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 (<math>n(0,t) = n(L,t) = 0</math>) e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto. | ||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
!colspan="2"|Evolução temporal da densidade do plasma para diferentes valores de <math>\nu_a</math> e <math>D_a</math> | !colspan="2"|Evolução temporal da densidade do plasma para diferentes valores de <math>\nu_a</math> =10 e <math>D_a</math> = 0.05 e 0.5 | ||
|- | |- | ||
|[[Arquivo:difusao_ambipolar_10_0.05.gif|thumb|upright=4|none|alt=Alt text|400px]] | |[[Arquivo:difusao_ambipolar_10_0.05.gif|thumb|upright=4|none|alt=Alt text|400px]] | ||
|[[Arquivo:difusao_ambipolar_10_0.5.gif|thumb|upright=4|none|alt=Alt text|400px]] | |[[Arquivo:difusao_ambipolar_10_0.5.gif|thumb|upright=4|none|alt=Alt text|400px]] | ||
|- | |||
|} | |||
Nos dois primeiros gráficos fixamos um valor de <math>\nu_a</math>, e variamos o valor de <math>D_a</math>. | |||
Como é possível observar os gráficos acima tem um comportamento de acordo com a eq.(3). O que já é esperado. Sabendo que por conta da frequência de colisão ser alta, o termo que carrega <math>u^2</math> da eq.(1), pode ser ignorado. | |||
{| class="wikitable" style="text-align: center;" | |||
!colspan="2"|Evolução temporal da densidade do plasma para diferentes valores de <math>\nu_a</math> =0.5 , 0.1 e <math>D_a</math> = 0.5 | |||
|- | |- | ||
|[[Arquivo:difusao_ambipolar_0.5_0.5.gif|thumb|upright=4|none|alt=Alt text|400px]] | |[[Arquivo:difusao_ambipolar_0.5_0.5.gif|thumb|upright=4|none|alt=Alt text|400px]] | ||
| Linha 110: | Linha 119: | ||
|- | |- | ||
|} | |} | ||
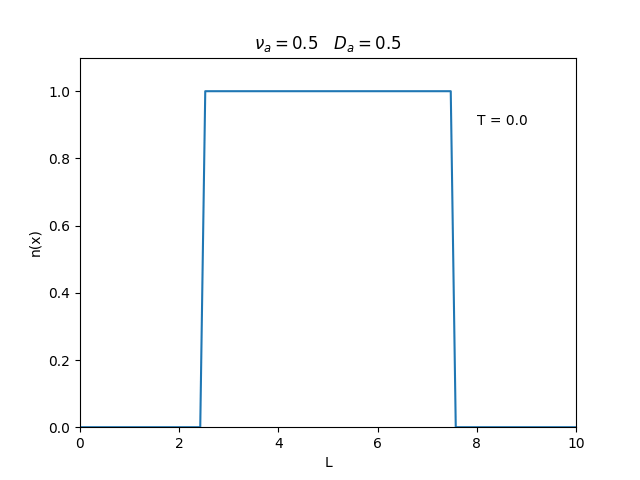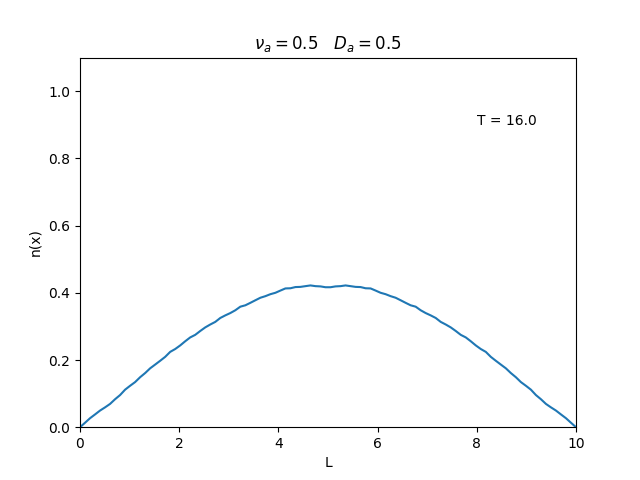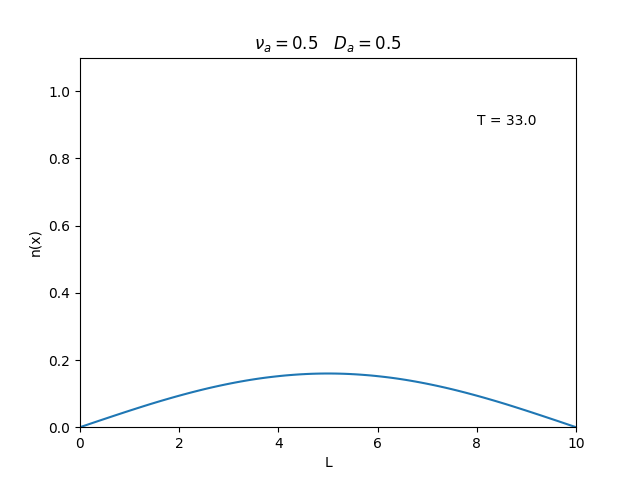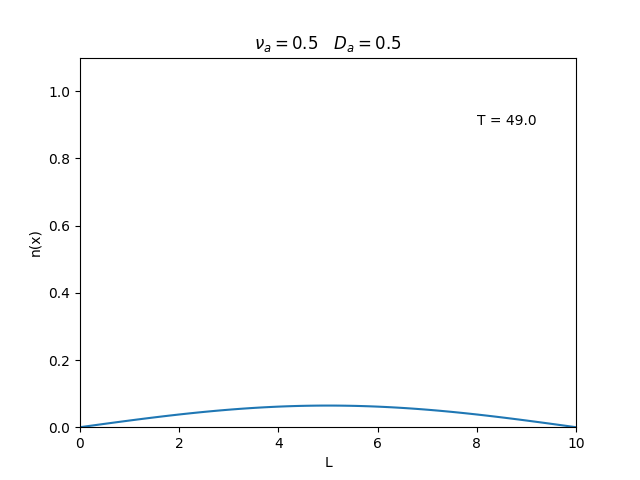
Fixamos um valor de <math>D_a</math>, e variamos o valor de <math>\nu_a</math>. | |||
Observamos um comportamento oscilatório. O que já é esperado, já que as colisões dos elétrons-íons nas partículas neutras é pequeno, assim, a difusão tem um caráter oscilatório. | |||
Nesse segundo caso usamos condições de contorno periódicas (<math>n_{I+1}^k = n_0^k</math>) e representa o caso de um tubo fechado. | |||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
| Linha 124: | Linha 139: | ||
Podemos observar que <math>D_a</math> é o parâmetro que domina a velocidade com que que a densidade decai, o que é esperado, uma vez que um coeficiente de difusão maior faz o plasma se difundir mais rápido. Já <math>\nu_a</math> | Podemos observar que <math>D_a</math> é o parâmetro que domina a velocidade com que que a densidade decai, o que é esperado, uma vez que um coeficiente de difusão maior faz o plasma se difundir mais rápido. | ||
Já <math>\nu_a</math> está relacionado à "suavidade" da distribuição, sendo que com frequências baixas começam a aparecer diversos picos de densidade e com frequências altas a densidade é uniforme. | |||
== Programas Utilizados == | == Programas Utilizados == | ||
| Linha 259: | Linha 276: | ||
</source> | </source> | ||
== Referências == | == Referências == | ||
<references/> | <references/> | ||
Edição atual tal como às 13h46min de 4 de julho de 2021
Equação da difusão ambipolar
Esse trabalho tem como objetivo demonstrar uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma(gás formado de elétrons e íons). A difusão é o modo como um fluido se dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas.
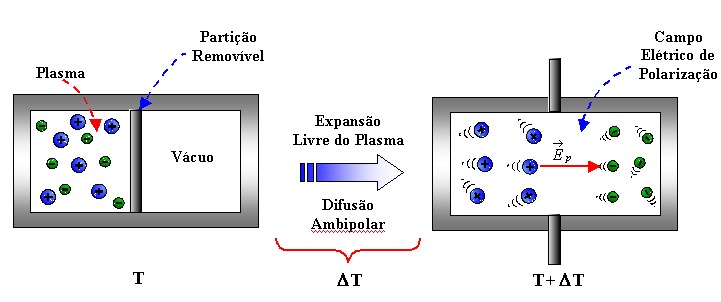
Quando a partição é removida ha uma pertubação instantanea na condição de equilibrio.Assim. ocorrendo uma expansão livre do plasma, os elétrons por ser mais leve difundem-se mais rápido que os íons devido a sua menor massa.
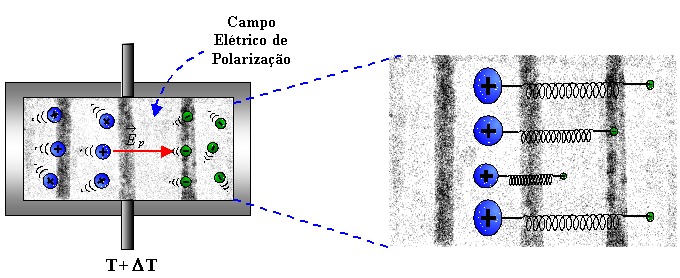
Essa separação de cargas gera um campo elétrico de polarização que aumenta a taxa de difusão dos íons e diminui a dos elétrons até que ocorra um equilíbrio. Por inércia, os elétrons se movem além da posição de equilíbrio, e um campo elétrico é produzido na direção oposta. Esta sequência de movimentos se repete periodicamente, resultando em rápidas oscilações coletivas dos elétrons sobre os íons.
Esses movimentos coletivos são caracterizados por uma frequência natural de oscilação(Oscilações de Langmuir).[1]
Como mostrado por Shimony e Cahn[2], esse problema é descrito por uma equação de onda amortecida para a função de densidade :
,
onde e , sendo a frequências de colisão dos íons e elétrons nas patículas neutras, chamada frequência de colisão ambipolar e o coeficiente de difusão ambipolar, que é calculado através de uma media dos coeficientes de difusão dos elétrons e íons.
Como tratamos do caso unidimensional, a equação 1 torna-se
.
Aproximações
As eq.(3) e (4) são termos da eq.(1), onde foram feitas algumas aproximações, produzido pelo livro do J.A Bittencourt [2]
Comparando as eq.(3) e (4),obtemos: . Observe que se >> 1, isto é, se os elétrons ou íons tem muitas colisões com partículas neutras durante o tempo característico para difusão . Então o termo que carrega na eq. (1) pode ser negligenciado. Como consequência durante todo tempo a concentração de elétrons e íons são iguais: , assim, a eq.(1) se reduz a seguinte equação de difusão:
O Método
A resolução numérica do problema foi baseada no artigo de Najafi e Izadi [3]. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional
.
Fizemos trocas de variáveis, para a melhor adaptação do método descrito no artigo. Assim chamamos, e .
Discretizando as variáveis do problema, temos que
,
.
Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos:
,
,
.
Substituindo essas relações na equação 6, obtemos:
.
Omitindo todos os temos de ordem e isolando , obtemos
,
sendo .
Essa é a equação para resolver o problema para , porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar a paritr de , para então calcular os demais passos. Para isso assumimos que a função é inicialmente estacionária e fazemos
Substituindo na equação 7 para obtemos
.
Com as equações 7 e 8, e tomando as devidas condições de contorno nas bordas (no caso desse trabalho usamos bordas fixas em 0 e também condições periódicas de contorno), podemos calcular a evolução temporal da função de densidade. Esse método é estável para e seu erro é
.
Resultados e Discussão
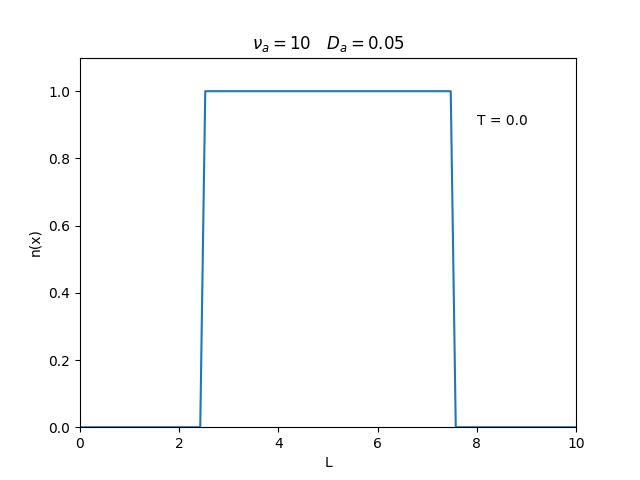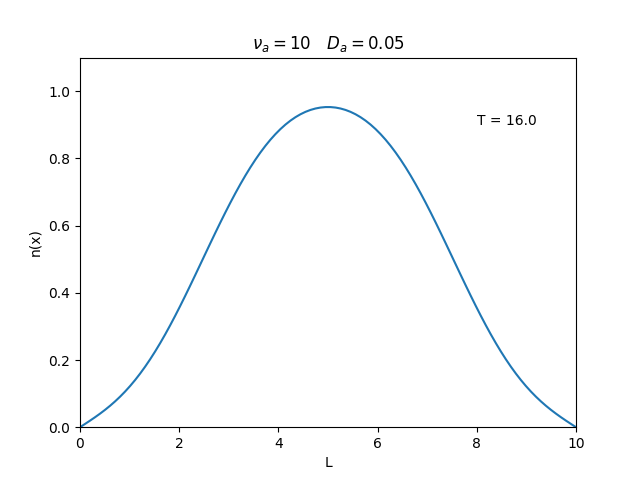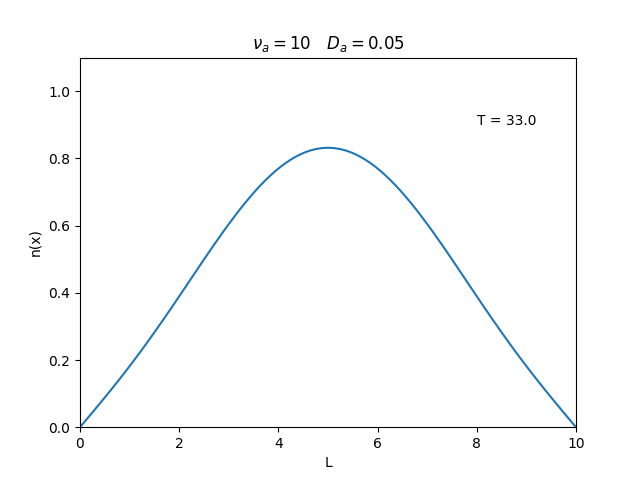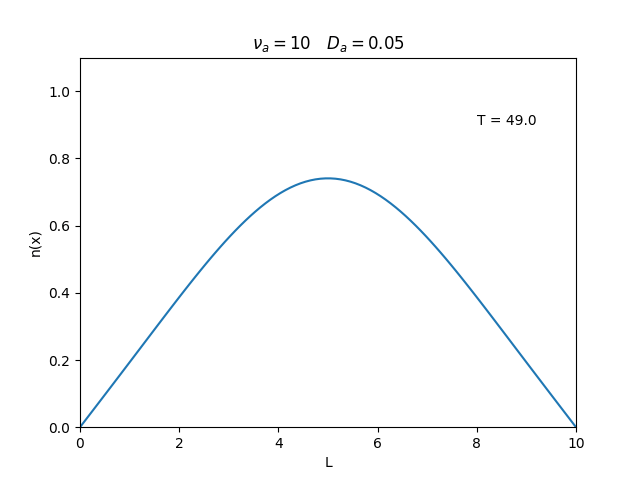
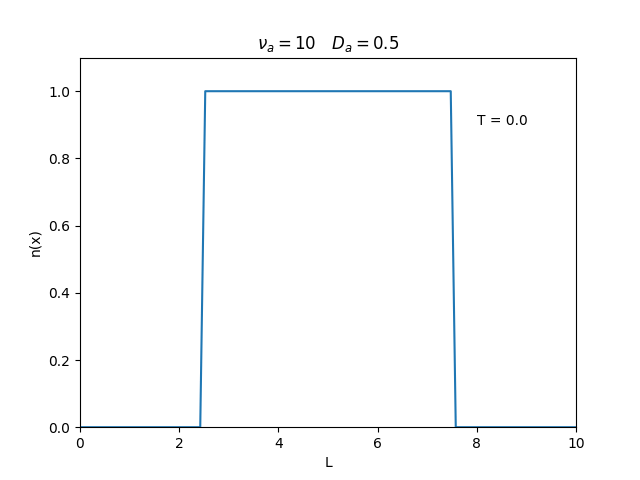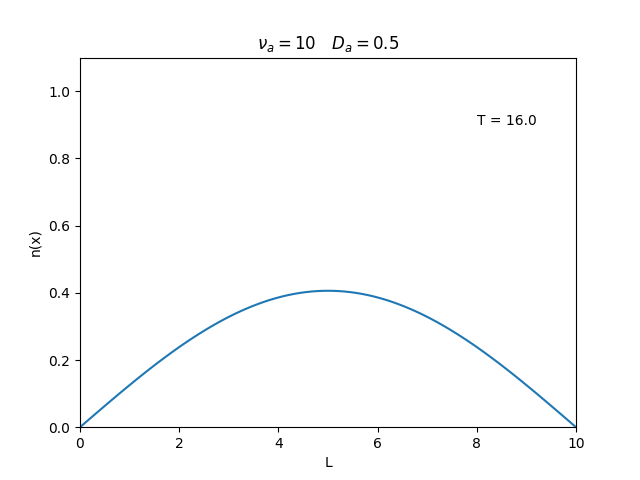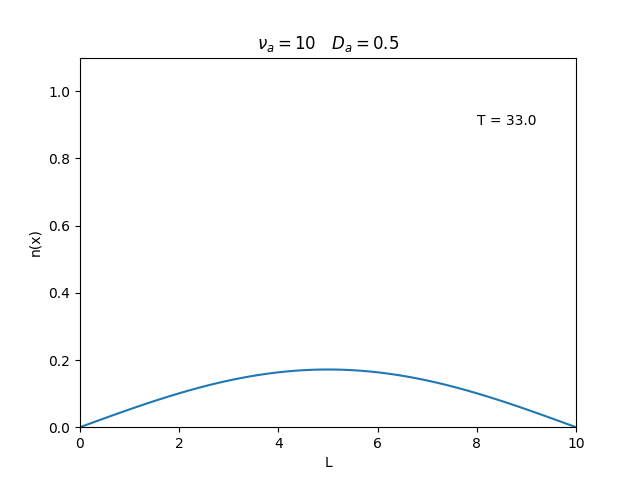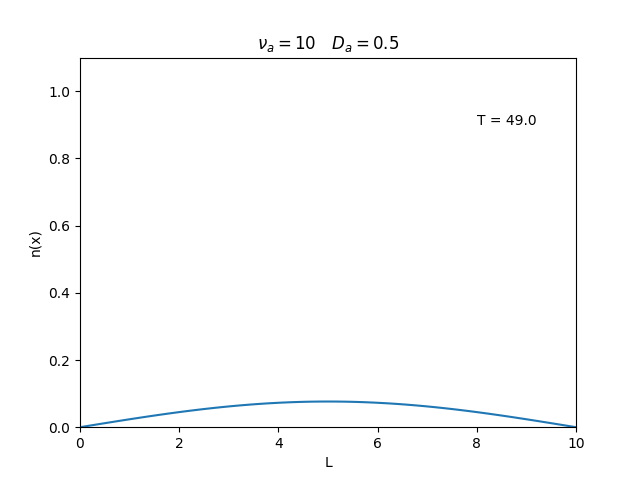
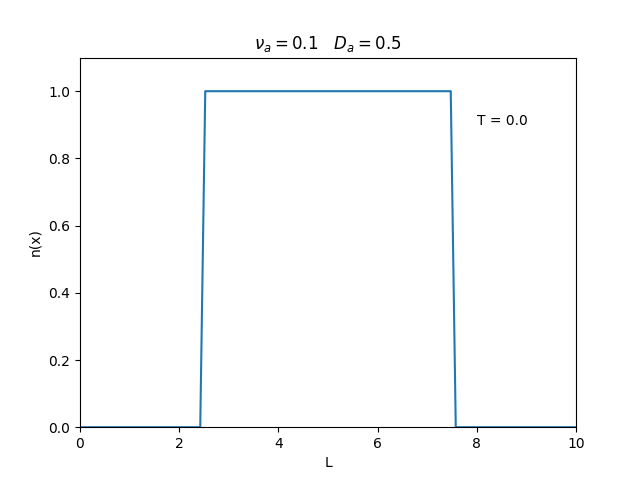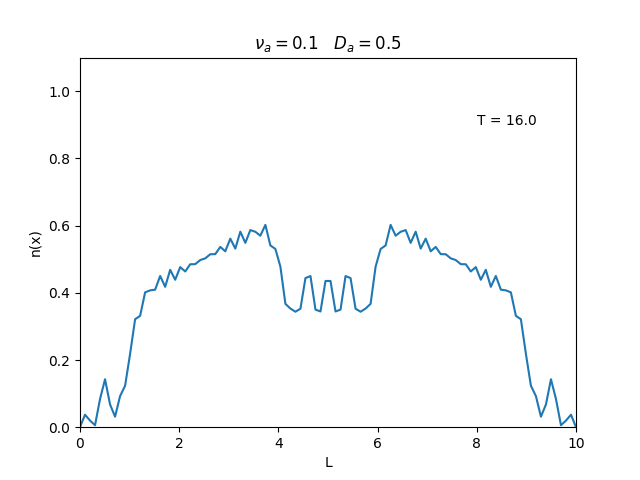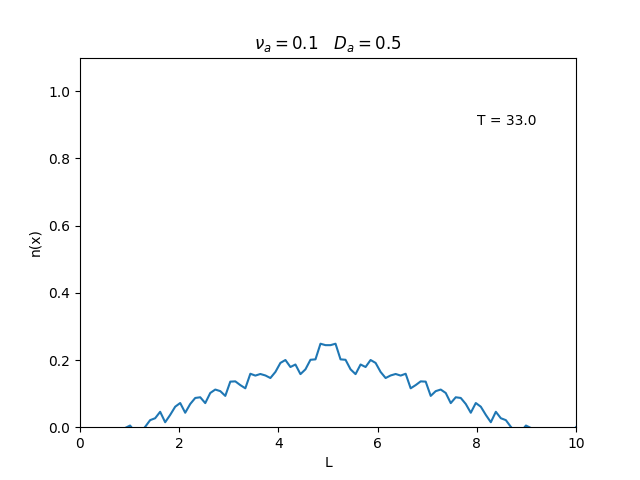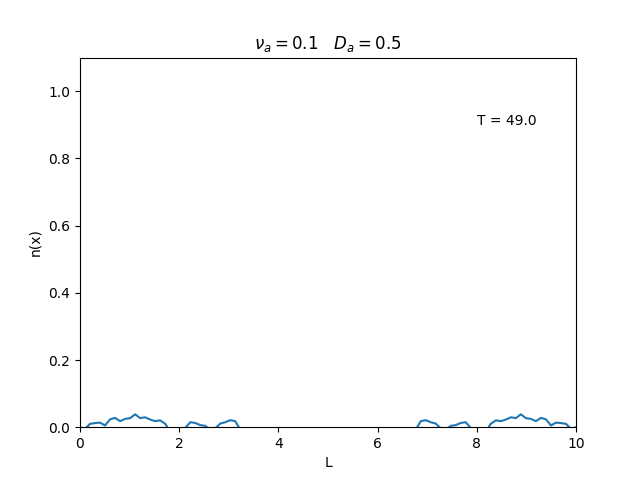
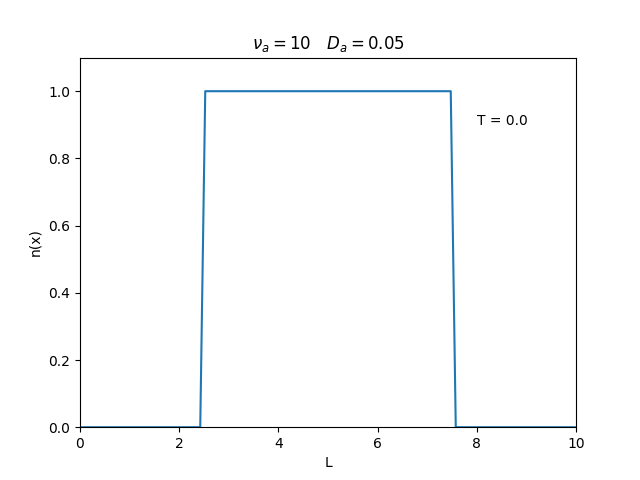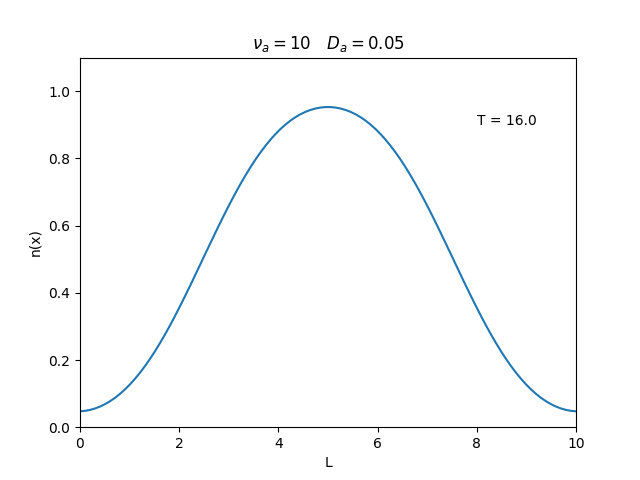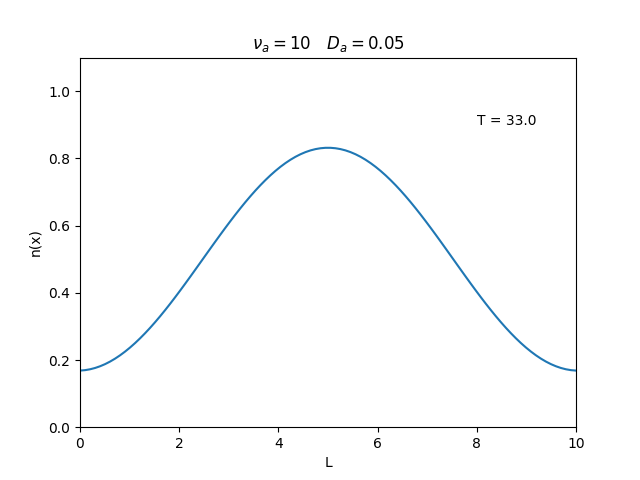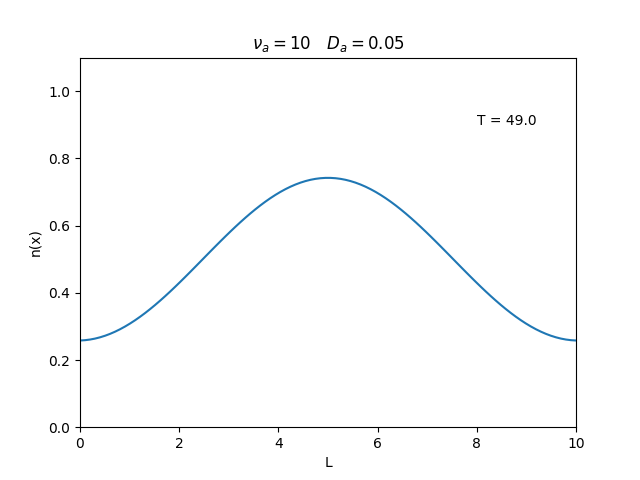
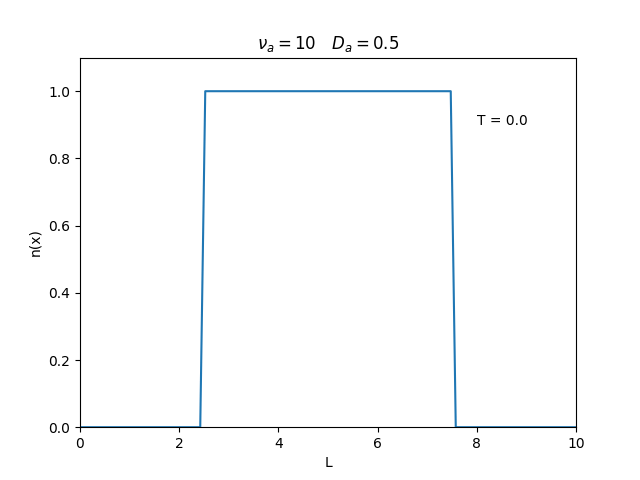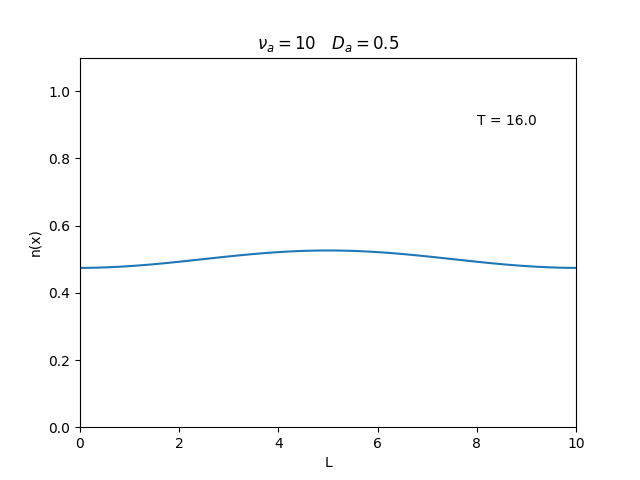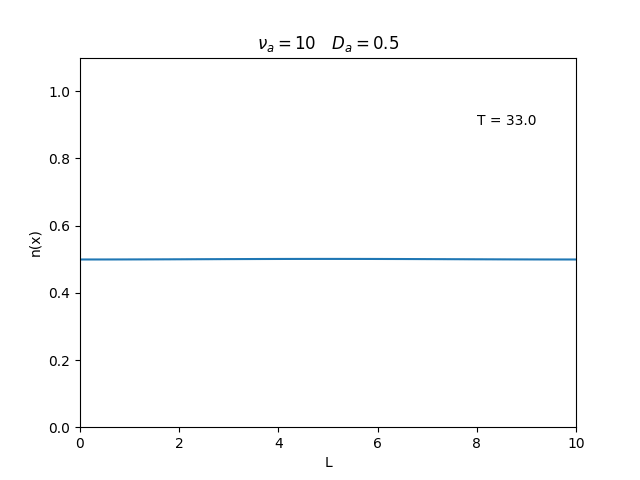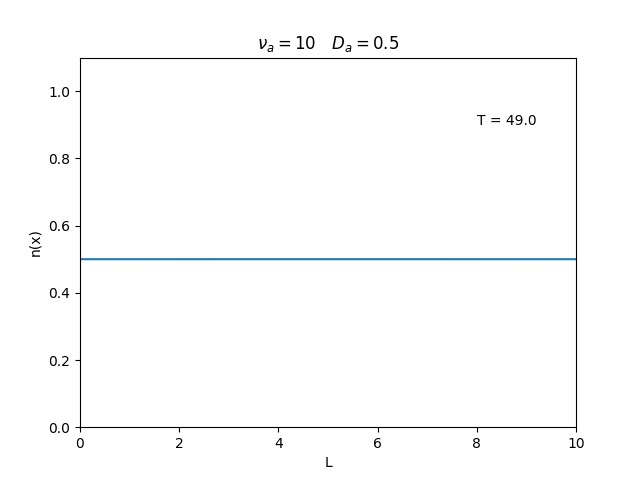
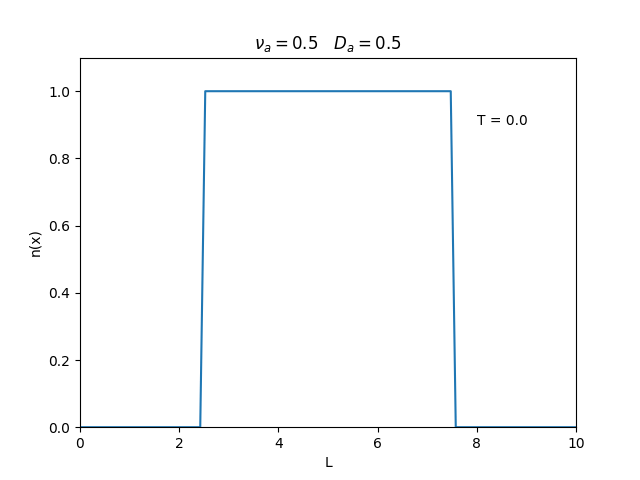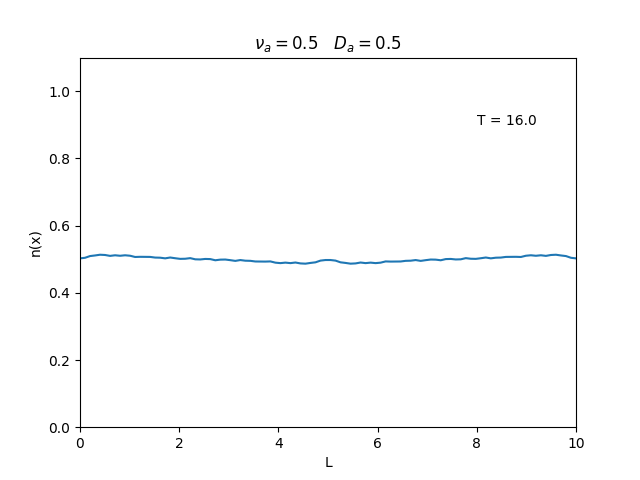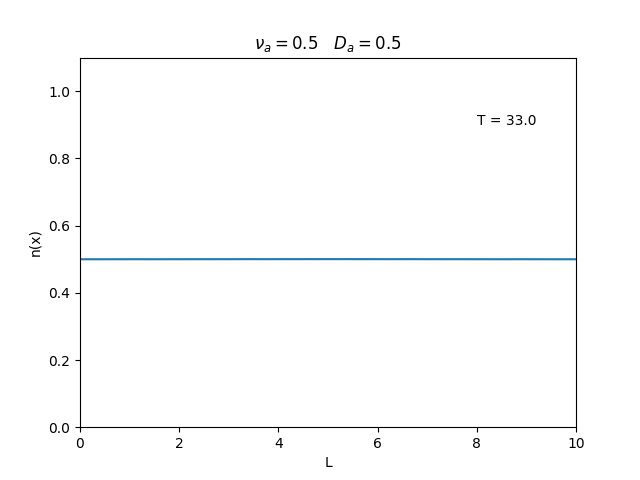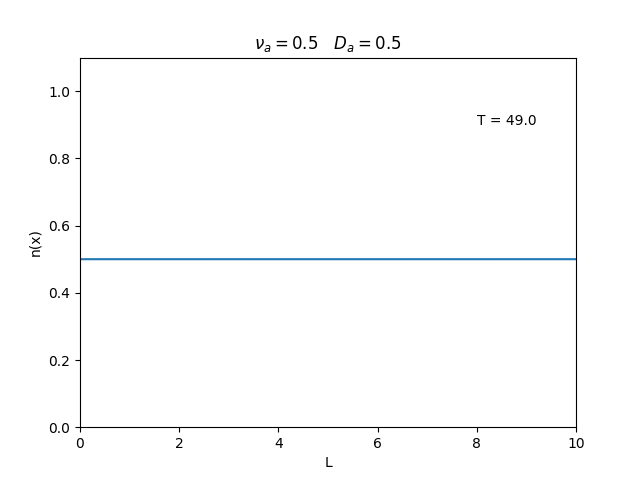
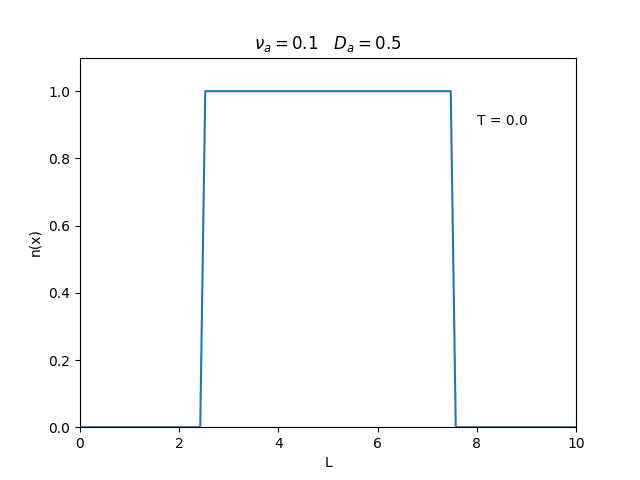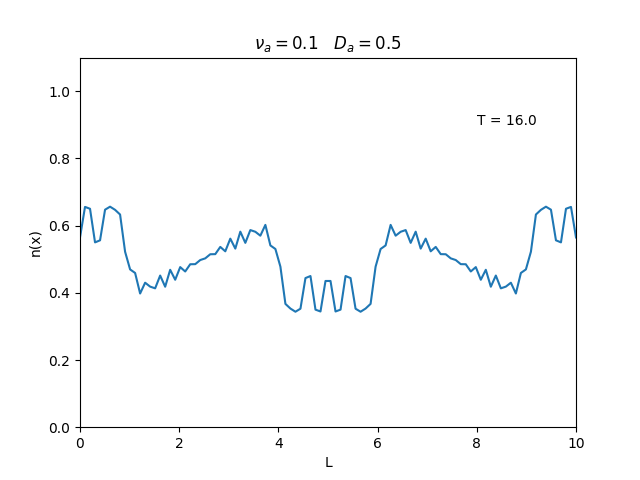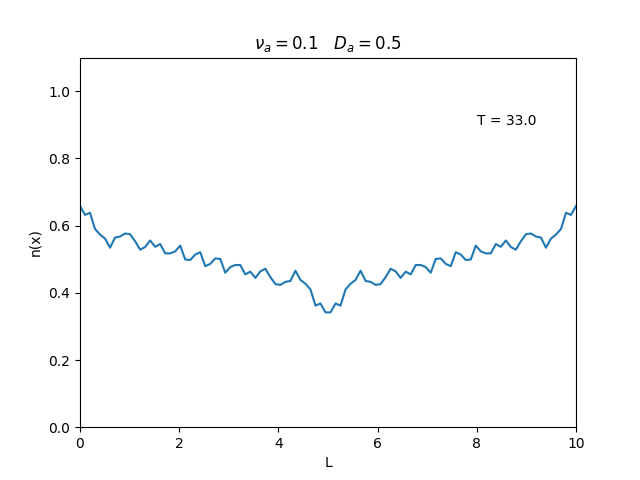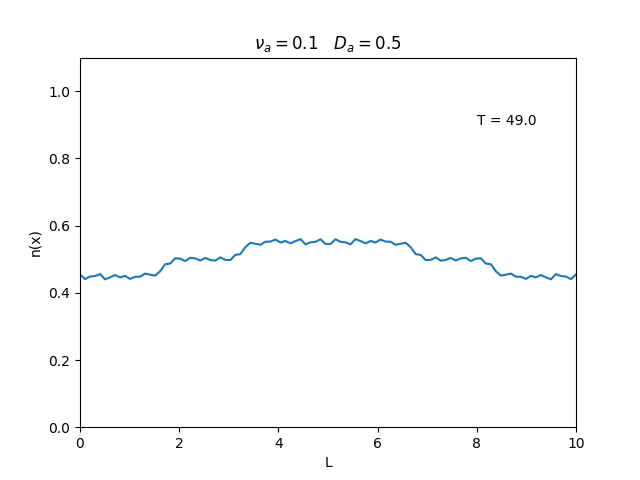
Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura . Fizemos o plasma inicialmente concentrado na região central do tubo: para e para fora dessa região. Usamos e , que resulta em , e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de e . Para garantir a estabilidade do método, essas constantes devem ser tais que .
Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 () e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto.
| Evolução temporal da densidade do plasma para diferentes valores de =10 e = 0.05 e 0.5 | |
|---|---|
Nos dois primeiros gráficos fixamos um valor de , e variamos o valor de . Como é possível observar os gráficos acima tem um comportamento de acordo com a eq.(3). O que já é esperado. Sabendo que por conta da frequência de colisão ser alta, o termo que carrega da eq.(1), pode ser ignorado.
| Evolução temporal da densidade do plasma para diferentes valores de =0.5 , 0.1 e = 0.5 | |
|---|---|
Fixamos um valor de , e variamos o valor de . Observamos um comportamento oscilatório. O que já é esperado, já que as colisões dos elétrons-íons nas partículas neutras é pequeno, assim, a difusão tem um caráter oscilatório.
Nesse segundo caso usamos condições de contorno periódicas () e representa o caso de um tubo fechado.
| Evolução temporal da densidade do plasma para diferentes valores de e | |
|---|---|
Podemos observar que é o parâmetro que domina a velocidade com que que a densidade decai, o que é esperado, uma vez que um coeficiente de difusão maior faz o plasma se difundir mais rápido.
Já está relacionado à "suavidade" da distribuição, sendo que com frequências baixas começam a aparecer diversos picos de densidade e com frequências altas a densidade é uniforme.
Programas Utilizados
Para implementar o método computacionalmente e criar os gifs foram usados códigos em python. O código abaixo é a solução para as bordas fixas em 0:
import numpy as np
import matplotlib.pyplot as plt
import imageio
dt = 0.01
dx = 0.1
L = 10
T = 50
#constantes do plasma
nu_a = 0.1
Da = 0.5
#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2
x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x))) #matriz com a densidade n(x,t)
#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()
#calculamos o próximo passo considerando dn/dt = 0 inicialmente
for i in range(1,len(x)-1):
n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))
#calculamos a posterior evolucao
for k in range(1, len(t)-1):
for i in range(1,len(x)-1): #isso fixa os contornos em 0
n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
plt.plot(x,n[k])
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.xlim([0,L])
plt.ylim([0,1.1])
plt.text(8,0.9,'T = '+str(k*dt))
plt.savefig('n_'+str(int(k*dt))+'.png')
plt.clf()
#criamos gifs usando os plots
images = []
for k in range(T):
images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'.gif', images, format='GIF', duration=1./10)
O código para as condições de contorno periódicas é levemente diferente, exigindo o acrécimo de duas duas linhas dentro do terceiro loop. Vale notar que aqui não nos preocupamos com o contorno no cáculo de porque a função nos contornos é 0 nos primeiros passos, independente de adotarmos ou não contornos periódicos.
import numpy as np
import matplotlib.pyplot as plt
import imageio
dt = 0.01
dx = 0.1
L = 10
T = 50
#constantes do plasma
nu_a = 0.1
Da = 0.5
#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2
x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x))) #matriz com a densidade n(x,t)
#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()
#calculamos o próximo passo considerando dn/dt = 0 inicialmente
for i in range(1,len(x)-1):
n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))
#calculamos a posterior evolucao
for k in range(1, len(t)-1):
for i in range(1,len(x)-1):
n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
#condicoes de contorno periodicas
n[k+1,0] = (1/(1+h*dt))*(2*(1-s)*n[k,0] - (1-h*dt)*n[k-1,0] + s*(n[k,1] + n[k,-1]))
n[k+1,-1] = (1/(1+h*dt))*(2*(1-s)*n[k,-1] - (1-h*dt)*n[k-1,-1] + s*(n[k,0] + n[k,-2]))
if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
plt.plot(x,n[k])
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.xlim([0,L])
plt.ylim([0,1.1])
plt.text(8,0.9,'T = '+str(k*dt))
plt.savefig('n_'+str(int(k*dt))+'.png')
plt.clf()
#criamos gifs usando os plots
images = []
for k in range(T):
images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'PBC.gif', images, format='GIF', duration=1./10)
Referências
- ↑ https://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172001000200011
- ↑ 2,0 2,1 Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) Erro de citação: Etiqueta inválida
<ref>; Nome "Simony+Cahn64" definido várias vezes com conteúdo diferente - ↑ H. Najafi and F. Izadi, "Comparison of two finite-difference methods for solving the damped wave equation", viXra, 2016























![{\displaystyle \left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93087b881e6f091b23454095fc236ac34ab6fa3)


![{\displaystyle n_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (7)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e06401f7906f810065d67beaf09b878739364135)






![{\displaystyle n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (8)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80c7be2e0f8d040af6935b4ccd810c05b4bce13d)