Difusão ambipolar em plasmas: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
== Equação da difusão ambipolar == | == Equação da difusão ambipolar == | ||
A difusão é o modo como um fluido de dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. Aqui mostramos uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma (gás formado de elétrons e íons) envolto em um gás neutro, ou seja, o caso de um plasma se espalhando por um tubo. | |||
Diferentemente de um gás de átomos/moléculas neutros(as), os plasmas são menos livres ao se moverem por causa das interações eletromagnéticas envolvidas no movimento das cargas, como a força de Coulomb e a força magnética. Na difusão de plasmas em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por | |||
<math> D_e = \frac{k_bT_e}{m_e\nu_e} </math> e <math> D_i = \frac{h_bT_i}{m_i\nu_i} </math> | <math> D_e = \frac{k_bT_e}{m_e\nu_e} </math> e <math> D_i = \frac{h_bT_i}{m_i\nu_i} </math> | ||
onde <math>T_e</math>, <math>T_i</math>, <math>m_e</math>, <math>m_i</math>, <math>\nu_e</math> e <math>\nu_i</math>, são as temperaturas, massas e frequências de colisão dos elétrons e íons com os | onde <math>T_e</math>, <math>T_i</math>, <math>m_e</math>, <math>m_i</math>, <math>\nu_e</math> e <math>\nu_i</math>, são as temperaturas, massas e frequências de colisão dos elétrons e íons com os átomos neutros. | ||
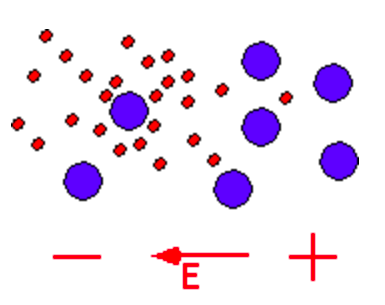
Devido à massa do elétron ser muito menor que a massa de um íon, <math>D_e</math> é maior que <math>D_i</math>, então quando um plasma começa a se | Devido à massa do elétron ser muito menor que a massa de um íon, <math>D_e</math> é maior que <math>D_i</math>, então quando um plasma começa a se difundir, incialmente os elétrons se espalham mais rapidamente que os íons, o que gera um campo elétrico que freia os elétron e acelera os íons. Chamamos esse processo de difusão ambipolar. | ||
[[Arquivo: Difusao_ambipolar.png|200 px]] <ref name=esquema> http://www.enigmatic-consulting.com/semiconductor_processing/CVD_Fundamentals/plasmas/ambipolar_diffusion.html </ref> | |||
Como mostrado por Shimony e Cahn<ref name=Simony+Cahn64> Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) </ref>, esse problema é descrito por uma equação de onda amortecida | Como mostrado por Shimony e Cahn<ref name=Simony+Cahn64> Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) </ref>, esse problema é descrito por uma equação de onda amortecida | ||
<math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> | <math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> | ||
onde <math>u^2 = \nu_a D_a</math> e <math>\alpha = 1/D_a</math>, sendo \nu_a a frequência de colisão ambipolar e D_a o coeficiente de difusão ambipolar, que pode ser escrito como <math>D_a = D_i(1+T_e/T_i)</math> <ref name=Da> http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf </ref>. | onde <math>u^2 = \nu_a D_a</math> e <math>\alpha = 1/D_a</math>, sendo <math>\nu_a</math> a frequência de colisão ambipolar e <math>D_a</math> o coeficiente de difusão ambipolar, que pode ser escrito como <math>D_a = D_i(1+T_e/T_i)</math> <ref name=Da> http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf </ref>. | ||
Como tratamos do caso unidimensional, a equação 1 torna-se | |||
<math>\frac{\partial^2 n(x,t)}{\partial x^2} = \frac{1}{u^2} \frac{\partial^2 n(x,t)}{\partial t^2} + \alpha \frac{\partial n(x,t)}{\partial t} \qquad (2)</math> | |||
== O Método == | == O Método == | ||
A resolução numérica do problema foi baseada no artigo de Najafi e Izadi <ref name=Najafi+Izadi16> H. Najafi and F. Izadi, "Comparison of two finite-difference methods for solving the | |||
damped wave equation", viXra, 2016 </ref>. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional | |||
<math> \frac{\partial^2 n(x,t)}{\partial t^2} + 2h \frac{\partial n(x,t)}{\partial t} = c^2 \frac{\partial^2 n(x,t)}{\partial x^2} \qquad (3) </math> | |||
No nosso caso <math>2h = \alpha u^2 = \nu_a</math> e <math>c^2 = u^2</math>. | |||
Discretizando as variáveis do problema, temos que | |||
<math>x_i = i\Delta x \qquad i = 0,1,2,...,I</math> | |||
<math>t_k = k\Delta t \qquad k = 0,1,2,...,K</math> | |||
Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos | |||
<math> \frac{\partial^2 n}{\partial t^2} |_i^k = \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^2 n}{\partial t^4}|_i^k + O(\Delta t^4) </math> | |||
<math> \frac{\partial n}{\partial t} |_i^k = \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4) </math> | |||
<math> \frac{\partial^2 n}{\partial x^2} |_i^k = \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^2 n}{\partial x^4}|_i^k + O(\Delta x^4) </math> | |||
Substituindo essas relações na equação 3, obtemos | |||
<math> \left[ \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k + O(\Delta t^4)\right] + 2h\left[ \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4)\right] = c^2\left[ \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O(\Delta x^4)\right] </math> | |||
Omitindo todos os temos de ordem <math>O{\Delta t^2,\Delta x^2}</math> e isolando <math>u_i^{k_1}</math>, obtemos | |||
<math> u_i^{k+1} = \frac{1}{1 + h\Delta t}[2(1-s)n_i^k - (1 - h\Delta t)n_i^{k-1} + s(n_{i+1}^k + n_{i-1}^k)] \qquad (4) </math> | |||
sendo <math> s = (c^2\Delta t^2/\Delta x^2) </math>. | |||
Essa é a equação para resolver o problema para <math>k \geq 1</math>, mas nessecitamos ainda de uma maneira de determinar <math>u_i^1</math> a paritr de <math>u_i^0</math>. Para isso assumimos que a função é inicialmente estacionária e fazemos | |||
<math>n_t(x,0) = 0 \Rightarrow \frac{n_i^1 - n_i^{-1}}{\Delta t} = 0 \Rightarrow n_i^1 = n_i^{-1}</math> | |||
Substituindo na equação 4 para <math>k = 0</math> obtemos | |||
<math> n_i^1 = \frac{1}{2}[2(1-s)n_i^0 + s(n_{i+1}^0 + n_{i-1}^0)] \qquad (5) </math> | |||
Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas, podemos calcular a evolução temporal da função de densidade. Esse método é estável para <math>0 \leq s \leq 1</math> e seu erro é | |||
<math> E\{n_i^k\} = - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k - \frac{h\Delta t^2}{3}\frac{\partial^3 n}{\partial t^3}|_i^k + c^2\frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O\{\Delta t^4, \Delta x^4\} </math> | |||
== Resultados e Discussão== | == Resultados e Discussão== | ||
Edição das 22h56min de 31 de março de 2021
Equação da difusão ambipolar
A difusão é o modo como um fluido de dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. Aqui mostramos uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma (gás formado de elétrons e íons) envolto em um gás neutro, ou seja, o caso de um plasma se espalhando por um tubo.
Diferentemente de um gás de átomos/moléculas neutros(as), os plasmas são menos livres ao se moverem por causa das interações eletromagnéticas envolvidas no movimento das cargas, como a força de Coulomb e a força magnética. Na difusão de plasmas em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por
e
onde , , , , e , são as temperaturas, massas e frequências de colisão dos elétrons e íons com os átomos neutros. Devido à massa do elétron ser muito menor que a massa de um íon, é maior que , então quando um plasma começa a se difundir, incialmente os elétrons se espalham mais rapidamente que os íons, o que gera um campo elétrico que freia os elétron e acelera os íons. Chamamos esse processo de difusão ambipolar.
Como mostrado por Shimony e Cahn[2], esse problema é descrito por uma equação de onda amortecida
onde e , sendo a frequência de colisão ambipolar e o coeficiente de difusão ambipolar, que pode ser escrito como [3].
Como tratamos do caso unidimensional, a equação 1 torna-se
O Método
A resolução numérica do problema foi baseada no artigo de Najafi e Izadi [4]. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional
No nosso caso e .
Discretizando as variáveis do problema, temos que
Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos
Substituindo essas relações na equação 3, obtemos
Omitindo todos os temos de ordem e isolando , obtemos
sendo .
Essa é a equação para resolver o problema para , mas nessecitamos ainda de uma maneira de determinar a paritr de . Para isso assumimos que a função é inicialmente estacionária e fazemos
Substituindo na equação 4 para obtemos
Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas, podemos calcular a evolução temporal da função de densidade. Esse método é estável para e seu erro é
Resultados e Discussão
Programas Utilizados
Referências
- ↑ http://www.enigmatic-consulting.com/semiconductor_processing/CVD_Fundamentals/plasmas/ambipolar_diffusion.html
- ↑ Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965)
- ↑ http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf
- ↑ H. Najafi and F. Izadi, "Comparison of two finite-difference methods for solving the damped wave equation", viXra, 2016

























![{\displaystyle \left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93087b881e6f091b23454095fc236ac34ab6fa3)


![{\displaystyle u_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa639b148175f1c3f4f9ce5640f6087e53b54729)






![{\displaystyle n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/296c55fd74de89c822e92dce454986bb832cb203)

