Difusão ambipolar em plasmas: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 12: | Linha 12: | ||
[[Arquivo: Difusao_ambipolar.png|200 px]] <ref name=esquema> http://www.enigmatic-consulting.com/semiconductor_processing/CVD_Fundamentals/plasmas/ambipolar_diffusion.html </ref> | [[Arquivo: Difusao_ambipolar.png|200 px]] <ref name=esquema> http://www.enigmatic-consulting.com/semiconductor_processing/CVD_Fundamentals/plasmas/ambipolar_diffusion.html </ref> | ||
Como mostrado por Shimony e Cahn<ref name=Simony+Cahn64> Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) </ref>, esse problema é descrito por uma equação de onda amortecida | Como mostrado por Shimony e Cahn<ref name=Simony+Cahn64> Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965) </ref>, esse problema é descrito por uma equação de onda amortecida para a função de densidade <math>n(\vec r, t)</math>: | ||
<math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> , | <math>\nabla^2 n(\vec r,t) = \frac{1}{u^2} \frac{\partial^2 n(\vec r,t)}{\partial t^2} + \alpha \frac{\partial n(\vec r,t)}{\partial t} \qquad (1)</math> , | ||
| Linha 27: | Linha 27: | ||
damped wave equation", viXra, 2016 </ref>. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional | damped wave equation", viXra, 2016 </ref>. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional | ||
<math> \frac{\partial^2 n(x,t)}{\partial t^2} + 2h \frac{\partial n(x,t)}{\partial t} = c^2 \frac{\partial^2 n(x,t)}{\partial x^2} \qquad (3) </math> | <math> \frac{\partial^2 n(x,t)}{\partial t^2} + 2h \frac{\partial n(x,t)}{\partial t} = c^2 \frac{\partial^2 n(x,t)}{\partial x^2} \qquad (3) </math>. | ||
| Linha 34: | Linha 34: | ||
Discretizando as variáveis do problema, temos que | Discretizando as variáveis do problema, temos que | ||
<math>x_i = i\Delta x \qquad i = 0,1,2,...,I</math> | <math>x_i = i\Delta x \qquad i = 0,1,2,...,I</math> , | ||
<math>t_k = k\Delta t \qquad k = 0,1,2,...,K</math> | <math>t_k = k\Delta t \qquad k = 0,1,2,...,K</math>. | ||
Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos | Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos | ||
<math> \frac{\partial^2 n}{\partial t^2} |_i^k = \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^2 n}{\partial t^4}|_i^k + O(\Delta t^4) </math> | <math> \frac{\partial^2 n}{\partial t^2} |_i^k = \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^2 n}{\partial t^4}|_i^k + O(\Delta t^4) </math> , | ||
<math> \frac{\partial n}{\partial t} |_i^k = \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4) </math> | <math> \frac{\partial n}{\partial t} |_i^k = \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4) </math> , | ||
<math> \frac{\partial^2 n}{\partial x^2} |_i^k = \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^2 n}{\partial x^4}|_i^k + O(\Delta x^4) </math> | <math> \frac{\partial^2 n}{\partial x^2} |_i^k = \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^2 n}{\partial x^4}|_i^k + O(\Delta x^4) </math>. | ||
Substituindo essas relações na equação 3, obtemos | Substituindo essas relações na equação 3, obtemos | ||
<math> \left[ \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k + O(\Delta t^4)\right] + 2h\left[ \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4)\right] = c^2\left[ \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O(\Delta x^4)\right] </math> | <math> \left[ \frac{n_i^{k+1} - 2n_i^k + n_i^{k-1}}{\Delta t^2} - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k + O(\Delta t^4)\right] + 2h\left[ \frac{n_i^{k+1} -n_i^{k-1}}{2\Delta t} - \frac{\Delta t^2}{6}\frac{\partial^3 n}{\partial t^3}|_i^k + O(\Delta t^4)\right] = c^2\left[ \frac{n_{i+1}^k - 2n_i^k + n_{i-1}^k}{\Delta x^2} - \frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O(\Delta x^4)\right] </math>. | ||
Omitindo todos os temos de ordem <math>O{\Delta t^2,\Delta x^2}</math> e isolando <math>u_i^{k_1}</math>, obtemos | Omitindo todos os temos de ordem <math>O\{\Delta t^2,\Delta x^2\}</math> e isolando <math>u_i^{k_1}</math>, obtemos | ||
<math> u_i^{k+1} = \frac{1}{1 + h\Delta t}[2(1-s)n_i^k - (1 - h\Delta t)n_i^{k-1} + s(n_{i+1}^k + n_{i-1}^k)] \qquad (4) </math> | <math> u_i^{k+1} = \frac{1}{1 + h\Delta t}[2(1-s)n_i^k - (1 - h\Delta t)n_i^{k-1} + s(n_{i+1}^k + n_{i-1}^k)] \qquad (4) </math> , | ||
sendo <math> s = (c^2\Delta t^2/\Delta x^2) </math>. | sendo <math> s = (c^2\Delta t^2/\Delta x^2) </math>. | ||
Essa é a equação para resolver o problema para <math>k \geq 1</math>, | Essa é a equação para resolver o problema para <math>k \geq 1</math>, porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar <math>u_i^1</math> a paritr de <math>u_i^0</math>, para então calcular os demais passos. Para isso assumimos que a função é inicialmente estacionária e fazemos | ||
<math>n_t(x,0) = 0 \Rightarrow \frac{n_i^1 - n_i^{-1}}{\Delta t} = 0 \Rightarrow n_i^1 = n_i^{-1}</math> | <math>n_t(x,0) = 0 \Rightarrow \frac{n_i^1 - n_i^{-1}}{\Delta t} = 0 \Rightarrow n_i^1 = n_i^{-1}</math>. | ||
Substituindo na equação 4 para <math>k = 0</math> obtemos | Substituindo na equação 4 para <math>k = 0</math> obtemos | ||
<math> n_i^1 = \frac{1}{2}[2(1-s)n_i^0 + s(n_{i+1}^0 + n_{i-1}^0)] \qquad (5) </math> | <math> n_i^1 = \frac{1}{2}[2(1-s)n_i^0 + s(n_{i+1}^0 + n_{i-1}^0)] \qquad (5) </math>. | ||
Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas, podemos calcular a evolução temporal da função de densidade. Esse método é estável para <math>0 \leq s \leq 1</math> e seu erro é | Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas (no caso desse trabalho usamos bordas fixas em 0 e também condições periódicas de contorno), podemos calcular a evolução temporal da função de densidade. Esse método é estável para <math>0 \leq s \leq 1</math> e seu erro é | ||
<math> E\{n_i^k\} = - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k - \frac{h\Delta t^2}{3}\frac{\partial^3 n}{\partial t^3}|_i^k + c^2\frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O\{\Delta t^4, \Delta x^4\} </math> | <math> E\{n_i^k\} = - \frac{\Delta t^2}{12}\frac{\partial^4 n}{\partial t^4}|_i^k - \frac{h\Delta t^2}{3}\frac{\partial^3 n}{\partial t^3}|_i^k + c^2\frac{\Delta x^2}{12}\frac{\partial^4 n}{\partial x^4}|_i^k + O\{\Delta t^4, \Delta x^4\} </math>. | ||
== Resultados e Discussão== | == Resultados e Discussão== | ||
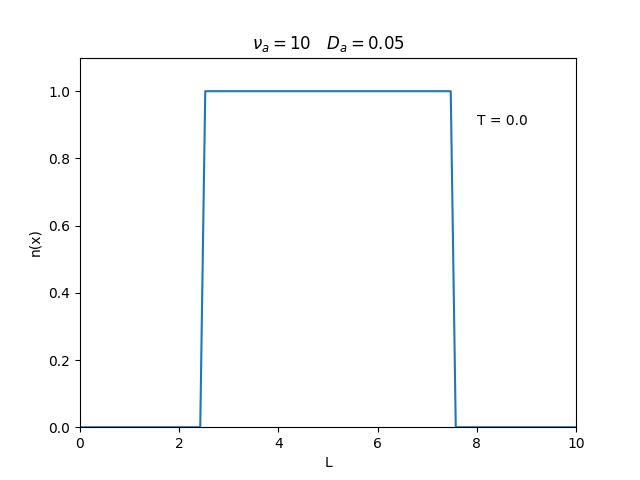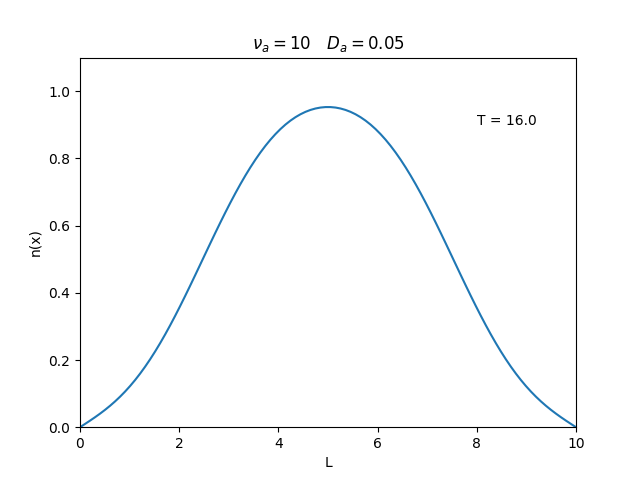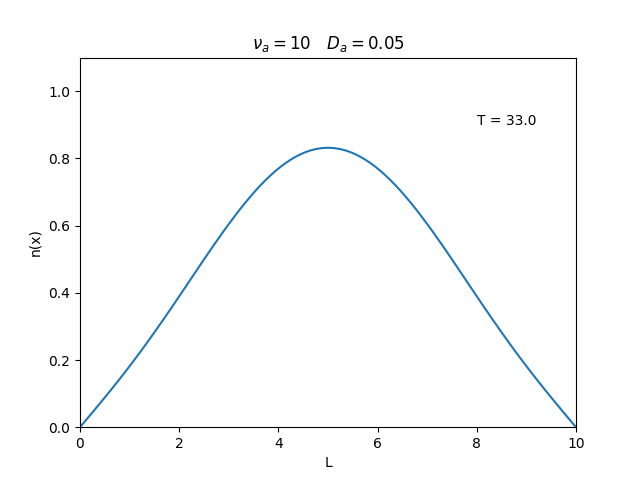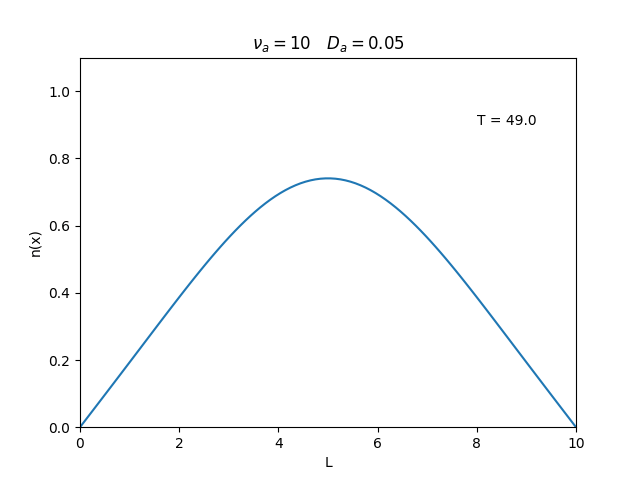
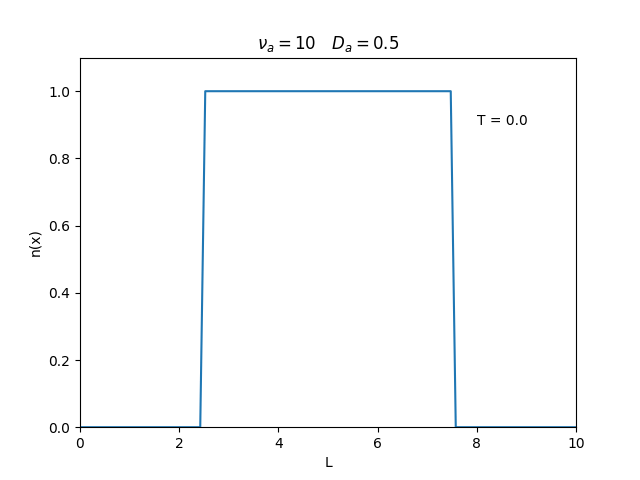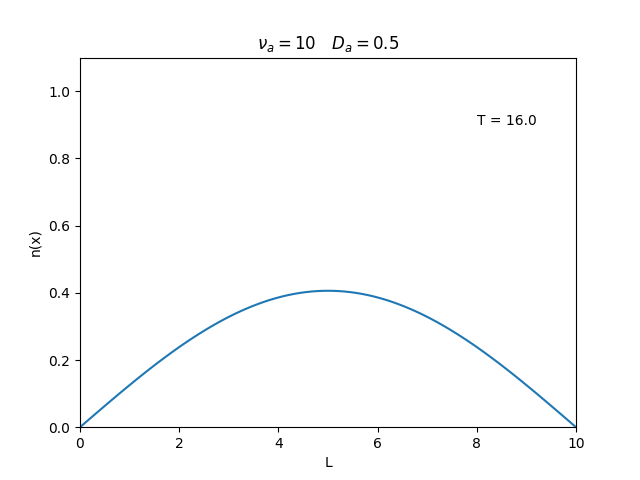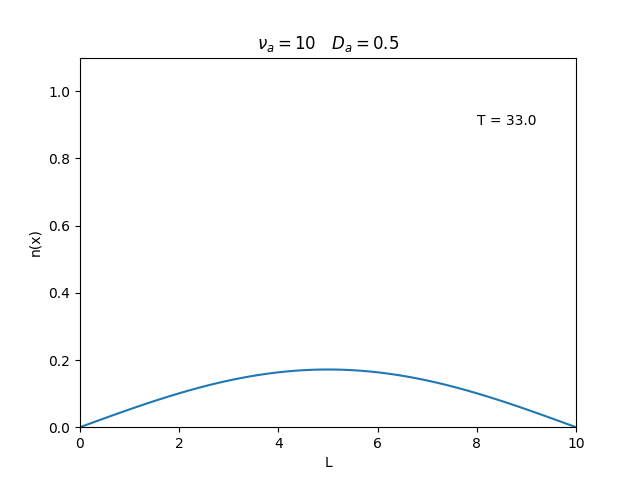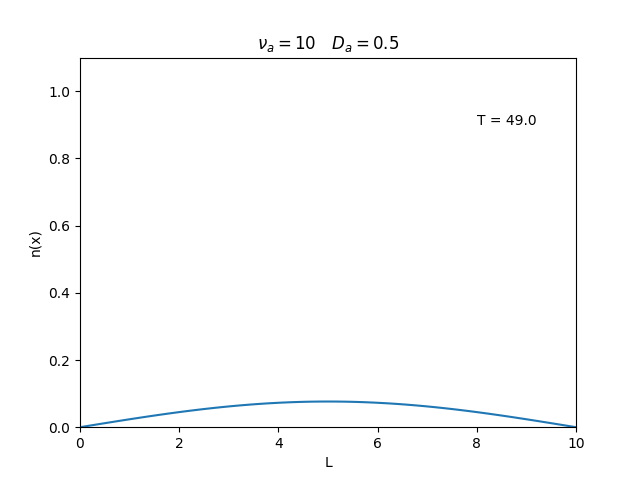
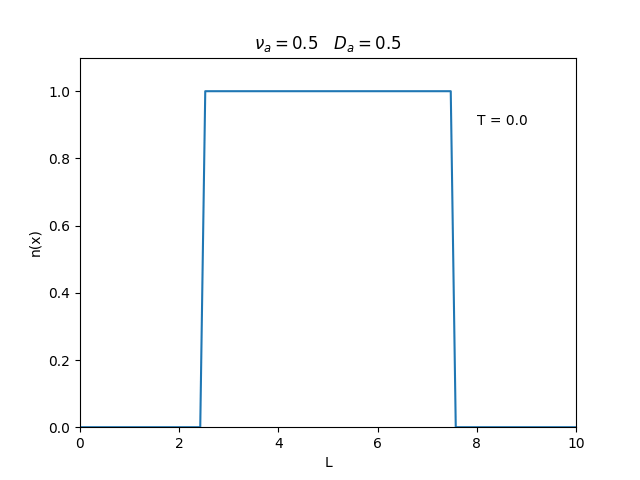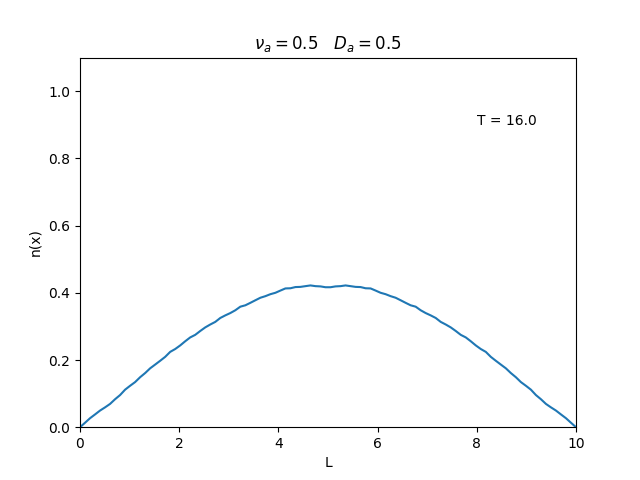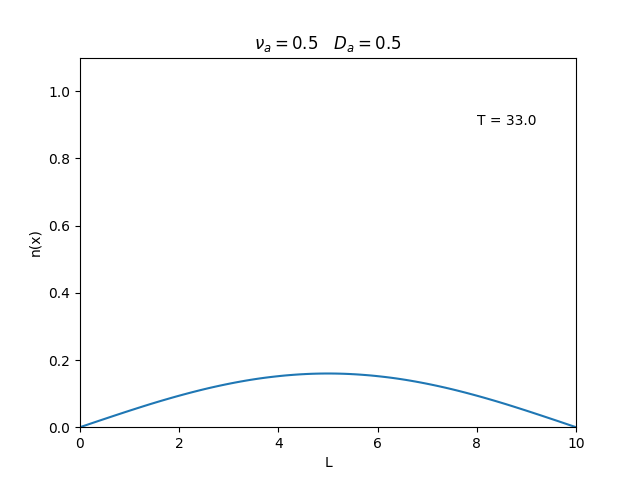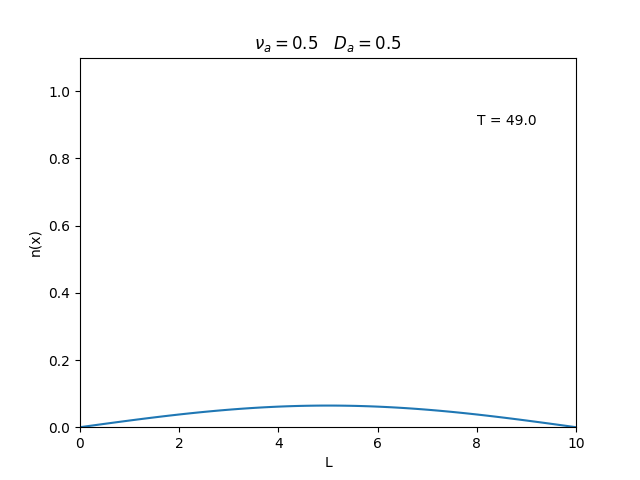
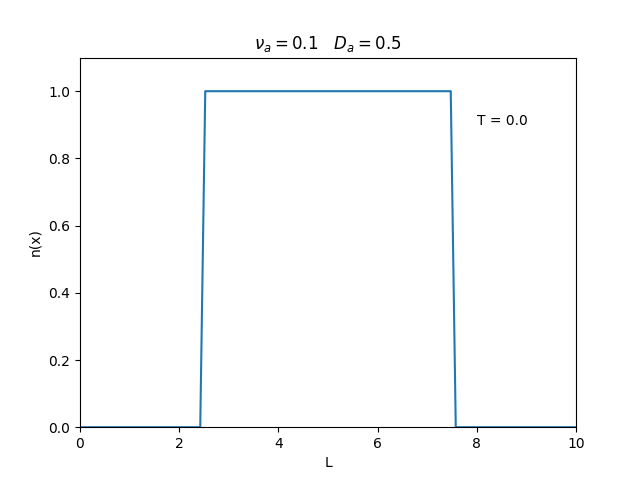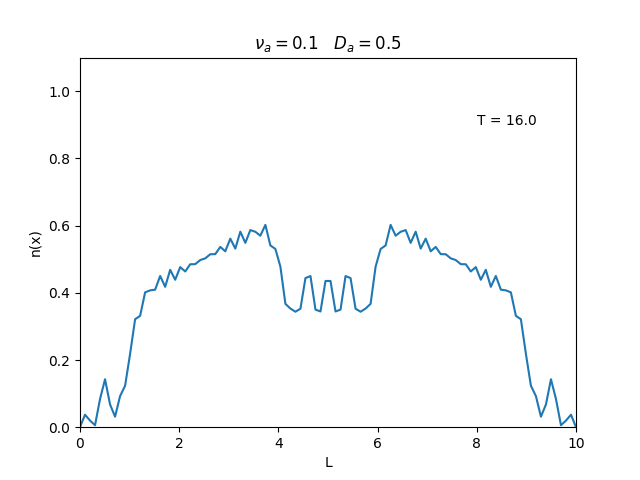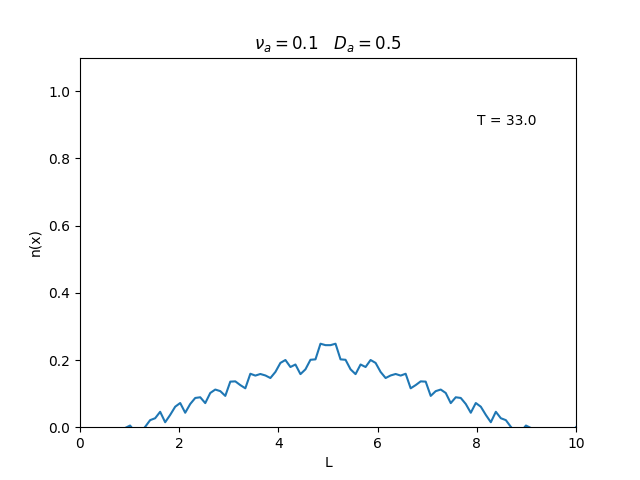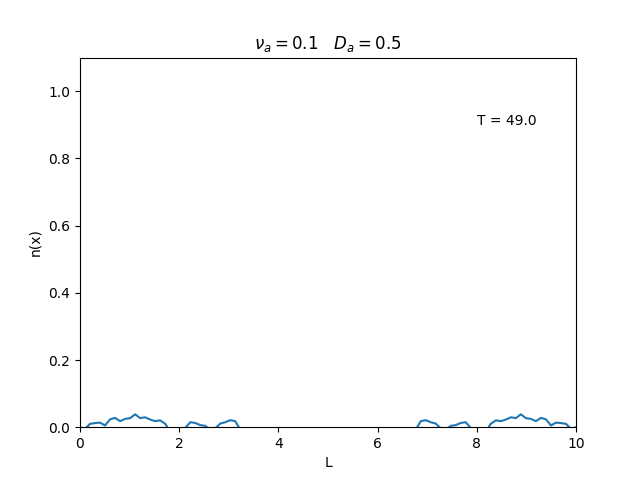
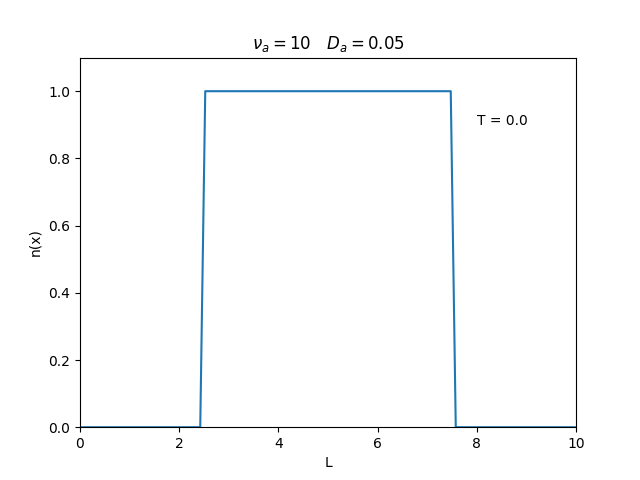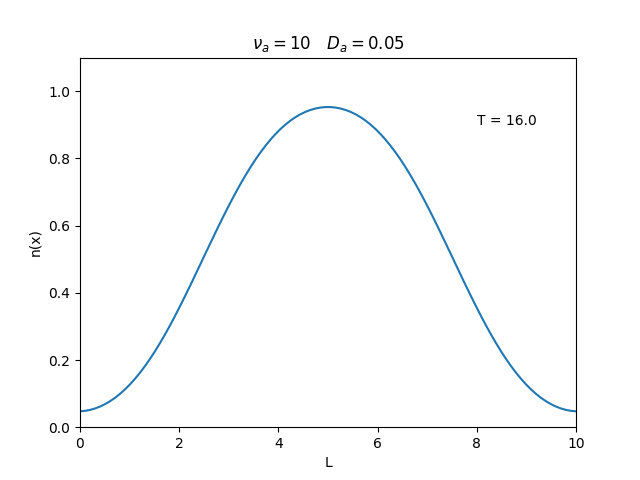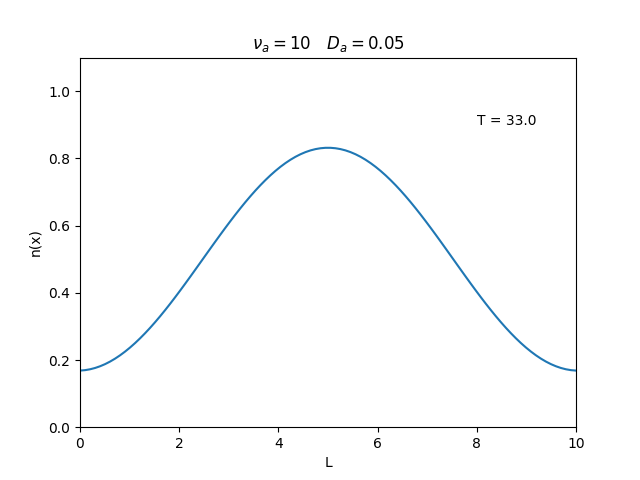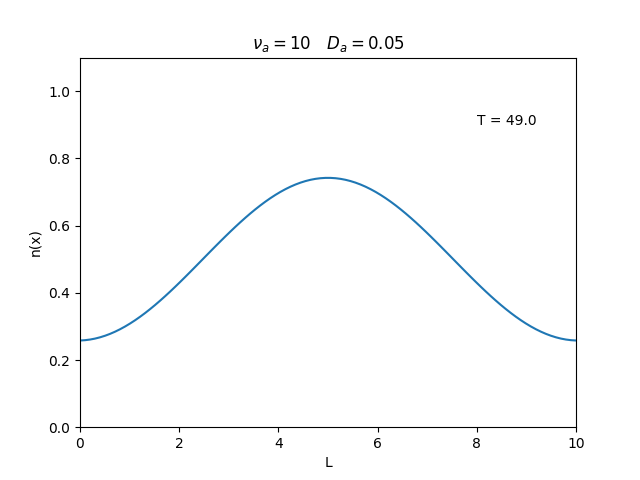
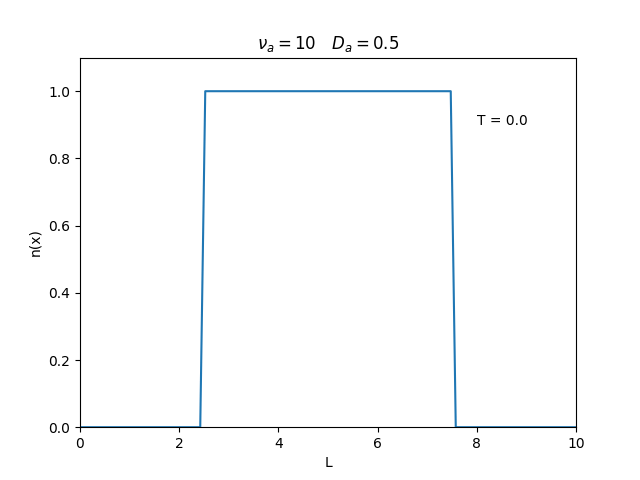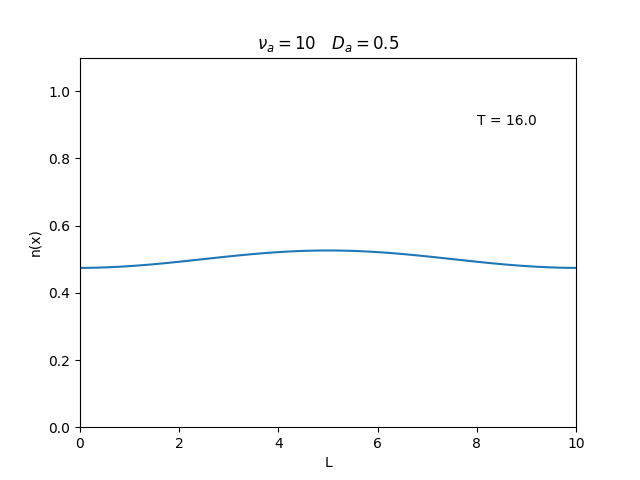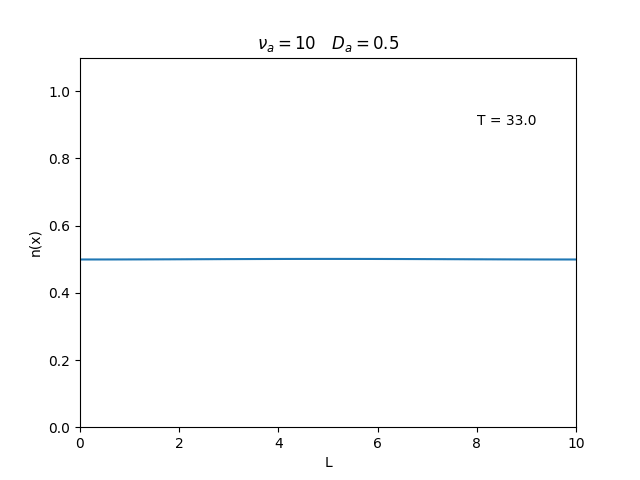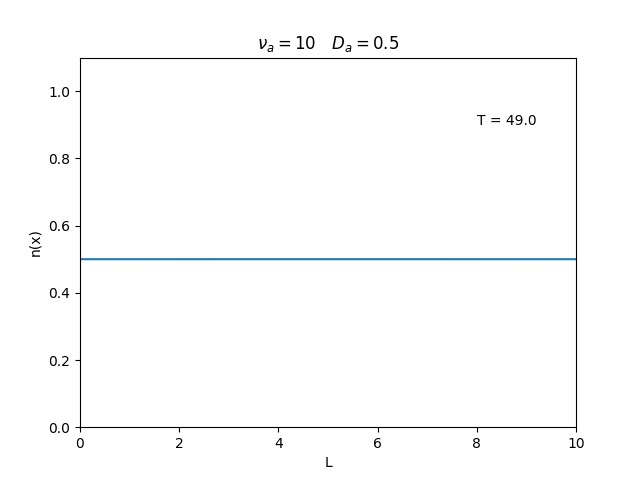
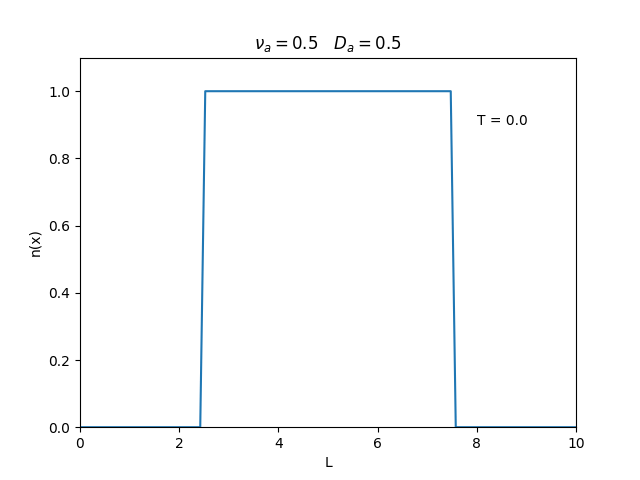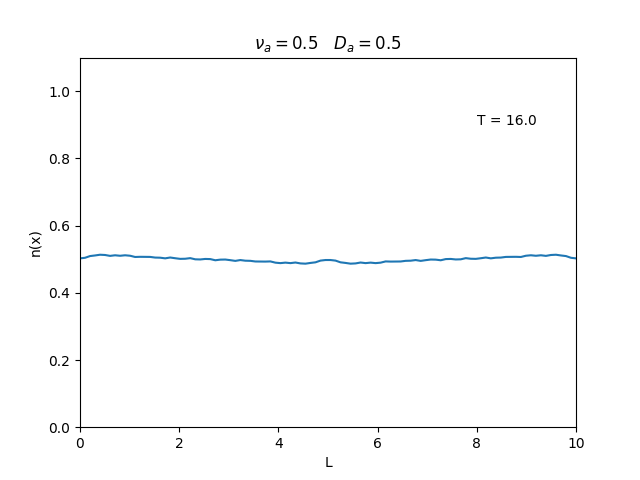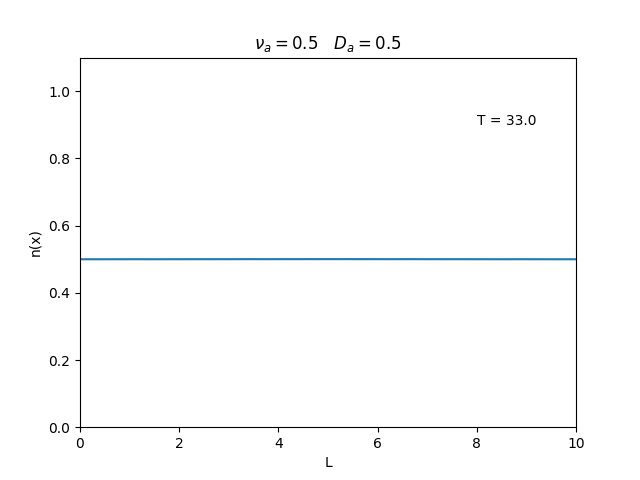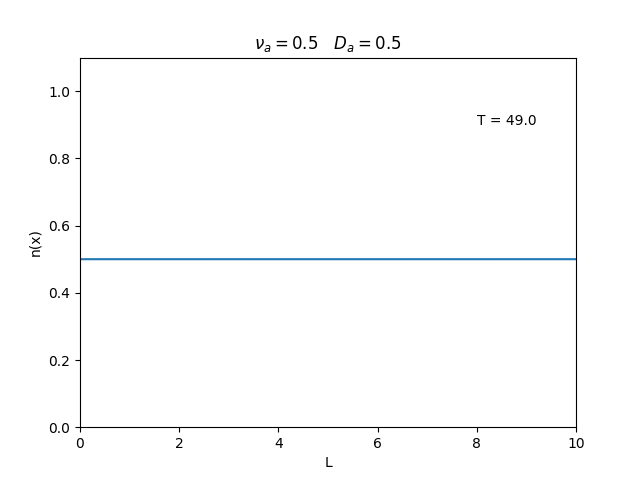
Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura <math>L=10</math>. Fizemos o plasma inicialmente concentrado na região central do tubo: <math>n(x,0)=1</math> para <math>L/4 \leq x \leq 3L/4</math> e <math>n(x,0)=0</math> para <math>x</math> fora dessa região. Usamos <math>\Delta x = 0.1</math> e <math>\Delta t = 0.01</math>, e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de <math>\nu_i</math> e <math>D_a</math>. Para garantir a estabilidade do método, essas constantes devem ser tais que <math> 0 \leq \nu_iD_a \leq (\Delta x / \Delta t)^2</math>. | Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura <math>L=10</math>. Fizemos o plasma inicialmente concentrado na região central do tubo: <math>n(x,0)=1</math> para <math>L/4 \leq x \leq 3L/4</math> e <math>n(x,0)=0</math> para <math>x</math> fora dessa região. Usamos <math>\Delta x = 0.1</math> e <math>\Delta t = 0.01</math>, que resulta em <math>s = 0.01\nu_aD_a</math>, e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de <math>\nu_i</math> e <math>D_a</math>. Para garantir a estabilidade do método, essas constantes devem ser tais que <math> 0 \leq \nu_iD_a \leq (\Delta x / \Delta t)^2</math>. | ||
Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 (<math>n(0,t) = n(L,t) = 0</math>) e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto. A segunda foi usando condições de contorno periódicas (<math>n_{I+1}^k = n_0^k</math>) e representa o caso de um tubo fechado. | Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 (<math>n(0,t) = n(L,t) = 0</math>) e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto. A segunda foi usando condições de contorno periódicas (<math>n_{I+1}^k = n_0^k</math>) e representa o caso de um tubo fechado. | ||
Edição das 13h39min de 5 de abril de 2021
Equação da difusão ambipolar
A difusão é o modo como um fluido se dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. Aqui mostramos uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma (gás formado de elétrons e íons) envolto em um gás neutro, ou seja, o caso de um plasma se espalhando por um tubo.
Diferentemente de um gás de átomos/moléculas neutros(as), os plasmas são menos livres ao se moverem por causa das interações eletromagnéticas envolvidas no movimento das cargas, como a força de Coulomb e a força magnética. Na difusão de plasmas em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por
e ,
onde , , , , e , são as temperaturas, massas e frequências de colisão dos elétrons e íons com os átomos neutros. Devido à massa do elétron ser muito menor que a massa de um íon, é maior que , então quando um plasma começa a se difundir, incialmente os elétrons se espalham mais rapidamente que os íons, o que gera um campo elétrico que freia os elétron e acelera os íons. Chamamos esse processo de difusão ambipolar.
Como mostrado por Shimony e Cahn[2], esse problema é descrito por uma equação de onda amortecida para a função de densidade :
,
onde e , sendo a frequência de colisão ambipolar e o coeficiente de difusão ambipolar, que pode ser escrito como [3].
Como tratamos do caso unidimensional, a equação 1 torna-se
.
O Método
A resolução numérica do problema foi baseada no artigo de Najafi e Izadi [4]. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional
.
No nosso caso e .
Discretizando as variáveis do problema, temos que
,
.
Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos
,
,
.
Substituindo essas relações na equação 3, obtemos
.
Omitindo todos os temos de ordem e isolando , obtemos
,
sendo .
Essa é a equação para resolver o problema para , porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar a paritr de , para então calcular os demais passos. Para isso assumimos que a função é inicialmente estacionária e fazemos
.
Substituindo na equação 4 para obtemos
.
Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas (no caso desse trabalho usamos bordas fixas em 0 e também condições periódicas de contorno), podemos calcular a evolução temporal da função de densidade. Esse método é estável para e seu erro é
.
Resultados e Discussão
Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura . Fizemos o plasma inicialmente concentrado na região central do tubo: para e para fora dessa região. Usamos e , que resulta em , e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de e . Para garantir a estabilidade do método, essas constantes devem ser tais que .
Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 () e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto. A segunda foi usando condições de contorno periódicas () e representa o caso de um tubo fechado.
| Evolução temporal da densidade do plasma para diferentes valores de e | |
|---|---|
| Evolução temporal da densidade do plasma para diferentes valores de e | |
|---|---|
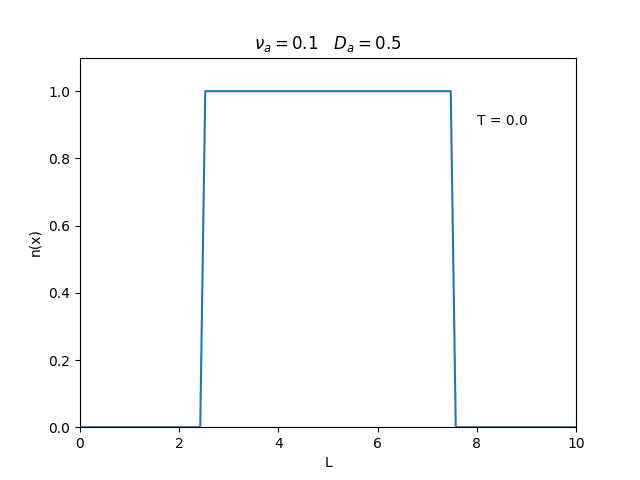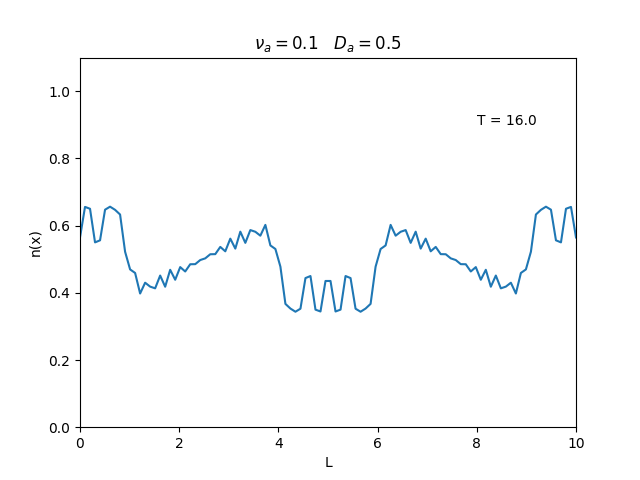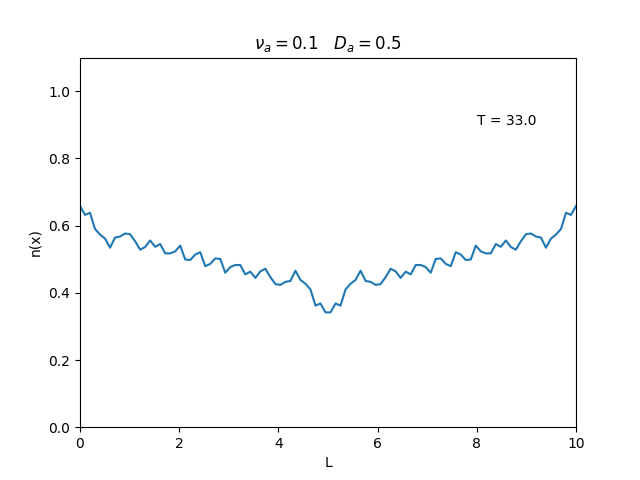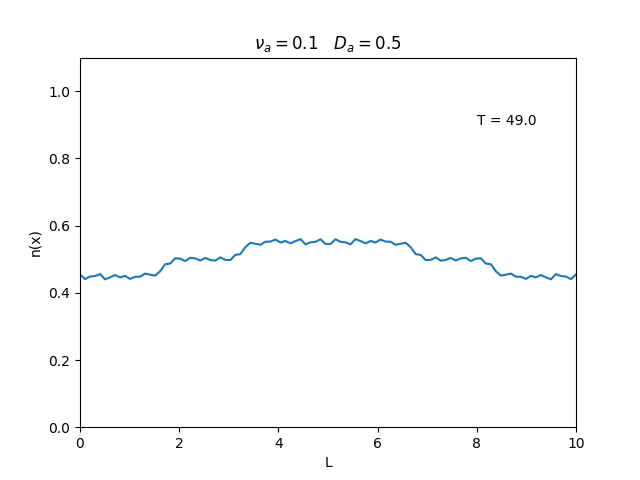
Podemos observar que é o parâmetro que domina a velocidade com que que a densidade decai, o que é esperado, uma vez que um coeficiente de difusão maior faz o plasma se difundir mais rápido. Já parece estar ligado à "suavidade" da distribuição, sendo que com frequências baixas começam a aparecer diversos picos de densidade.
Programas Utilizados
Para implementar o método computacionalmente e criar os gifs foram usados códigos em python. O código abaixo é a solução para as bordas fixas em 0:
import numpy as np
import matplotlib.pyplot as plt
import imageio
dt = 0.01
dx = 0.1
L = 10
T = 50
#constantes do plasma
nu_a = 0.1
Da = 0.5
#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2
x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x))) #matriz com a densidade n(x,t)
#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()
#calculamos o próximo passo considerando dn/dt = 0 inicialmente
for i in range(1,len(x)-1):
n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))
#calculamos a posterior evolucao
for k in range(1, len(t)-1):
for i in range(1,len(x)-1): #isso fixa os contornos em 0
n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
plt.plot(x,n[k])
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.xlim([0,L])
plt.ylim([0,1.1])
plt.text(8,0.9,'T = '+str(k*dt))
plt.savefig('n_'+str(int(k*dt))+'.png')
plt.clf()
#criamos gifs usando os plots
images = []
for k in range(T):
images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'.gif', images, format='GIF', duration=1./10)
O código para as condições de contorno periódicas é levemente diferente, exigindo o acrécimo de duas duas linhas dentro do terceiro loop. Vale notar que aqui não nos preocupamos com o contorno no cáculo de porque a função nos contornos é 0 nos primeiros passos, independente de adotarmos ou não contornos periódicos.
import numpy as np
import matplotlib.pyplot as plt
import imageio
dt = 0.01
dx = 0.1
L = 10
T = 50
#constantes do plasma
nu_a = 0.1
Da = 0.5
#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2
x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x))) #matriz com a densidade n(x,t)
#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()
#calculamos o próximo passo considerando dn/dt = 0 inicialmente
for i in range(1,len(x)-1):
n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))
#calculamos a posterior evolucao
for k in range(1, len(t)-1):
for i in range(1,len(x)-1):
n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
#condicoes de contorno periodicas
n[k+1,0] = (1/(1+h*dt))*(2*(1-s)*n[k,0] - (1-h*dt)*n[k-1,0] + s*(n[k,1] + n[k,-1]))
n[k+1,-1] = (1/(1+h*dt))*(2*(1-s)*n[k,-1] - (1-h*dt)*n[k-1,-1] + s*(n[k,0] + n[k,-2]))
if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
plt.plot(x,n[k])
plt.title(r'$\nu_a=$'+str(nu_a)+' $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.xlim([0,L])
plt.ylim([0,1.1])
plt.text(8,0.9,'T = '+str(k*dt))
plt.savefig('n_'+str(int(k*dt))+'.png')
plt.clf()
#criamos gifs usando os plots
images = []
for k in range(T):
images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'PBC.gif', images, format='GIF', duration=1./10)
Referências
- ↑ http://www.enigmatic-consulting.com/semiconductor_processing/CVD_Fundamentals/plasmas/ambipolar_diffusion.html
- ↑ Z. Shimony and J. H. Cahn, "Time-dependent ambipolar diffusion waves", The Physics of Fluids 8, 1704 (1965)
- ↑ . http://uigelz.eecs.umich.edu/classes/pub/eecs517/handouts/derivation_ambipolar_diffusion_v02.pdf
- ↑ H. Najafi and F. Izadi, "Comparison of two finite-difference methods for solving the damped wave equation", viXra, 2016



























![{\displaystyle \left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93087b881e6f091b23454095fc236ac34ab6fa3)


![{\displaystyle u_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa639b148175f1c3f4f9ce5640f6087e53b54729)






![{\displaystyle n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/296c55fd74de89c822e92dce454986bb832cb203)