Corda Vibrante: mudanças entre as edições
(Inicio da análise espectral) |
(→Notas) |
||
| (108 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo :''' Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa. | |||
== A equação da onda == | == A equação da onda == | ||
No estudo das oscilações, é comum entre os físicos o emprego de modelos simples como representações "prototípicas" de certos padrões básicos observados na natureza. A eficácia desses modelos simples decorre de duas características fundamentais: a capacidade de serem compreendidos em detalhes minuciosos e a habilidade de reproduzir comportamentos semelhantes aos de situações reais e mais complexas, auxiliando na compreensão destas, pelo menos em termos qualitativos. | |||
Quando se trata de comportamentos oscilatórios, o modelo mais comumente utilizado é o do sistema massa-mola. Por outro lado, para descrever comportamentos ondulatórios unidimensionais, o modelo simples mais difundido é o da corda vibrante. | |||
=== Dedução === | |||
Consideremos uma corda esticada, como a corda de um violão, por exemplo. Suponhamos que esta corda tenha um comprimento <math> L </math> e que suas extremidades estejam fixas nos pontos <math> x = 0 </math> e <math> x = L </math>. Além disso, vamos supor que a corda tenha uma densidade linear uniforme representada por <math> \mu = \frac{\Delta{m}}{\Delta{x}} </math>, e que esteja sob uma tensão constante <math> T </math>. | |||
Assumindo que a corda realize vibrações transversais apenas na direção <math> y </math> (embora possa ter vibrações transversais na direção <math> z </math>, as quais vamos ignorar aqui), podemos representar a configuração da corda em qualquer instante de tempo no plano <math> xy </math> por uma função <math> y(x,t) </math>. | |||
Vamos considerar mais algumas suposições: | |||
I) A tensão <math> T </math> que estica a corda é tão alta que podemos negligenciar a força gravitacional sobre ela; | |||
II) A corda é perfeitamente elástica, ou seja, não oferece resistência a dobras; | |||
III) Os deslocamentos da corda, que ocorrem apenas na direção <math> y </math>, são de pequena amplitude. | |||
Com essas suposições em mente, estamos prontos para abordar o problema da corda vibrante. Em qualquer instante de tempo, um segmento arbitrário da corda estará na posição geral indicada pela figura abaixo: | |||
[[Arquivo:posicao_generica.png|400px|thumb|center|Posição genérica de um pedaço qualquer da corda]] | |||
A massa do pequeno segmento de corda de comprimento <math> \Delta{x} </math> é | |||
<center> | |||
<math> | |||
\Delta{m} = \mu \Delta{x}. | |||
</math> | |||
</center> | |||
As componentes horizontal e vertical da força resultante atuando sobre esse segmento são: | |||
<center> | |||
<math> | |||
F_x = T \cos{(\theta + \Delta{\theta})} - T \cos{(\theta)} | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
F_y = T \sin{(\theta + \Delta{\theta})} - T \sin{(\theta)}. | |||
</math> | |||
</center> | |||
Estamos assumindo que a corda não se move na direção <math> x </math> (apenas na direção <math> y </math>). Isso implica que a força resultante na direção <math> x </math> é nula (<math> F_x = 0 </math>). Substituindo essa condição na equação, obtemos: | |||
<center> | |||
<math> | |||
\cos{(\theta + \Delta{\theta})} = \cos{(\theta)}. | |||
</math> | |||
</center> | |||
E a força resultante na direção <math> y </math>, <math> F_y </math>, é dada de acordo com a segunda lei de Newton: | |||
<center> | |||
<math> | |||
F_y = (\mu \Delta{x})a_y = (\mu \Delta{x}) \frac{\partial^2{y}}{\partial{t^2}}, | |||
</math> | |||
</center> | |||
então: | |||
<center> | |||
<math> | |||
T \sin{(\theta + \Delta{\theta})} - T \sin{(\theta)} = (\mu \Delta{x}) \frac{\partial^2{y}}{\partial{t^2}}, | |||
</math> | |||
</center> | |||
ou | |||
<center> | |||
<math> | |||
\sin{(\theta + \Delta{\theta})} - \sin{(\theta)} = \Delta{x} \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}}. | |||
</math> | |||
</center> | |||
Vamos prosseguir dividindo os dois lados da equação acima pelo termo <math> \cos{(\theta)} </math>, sabendo que <math> \cos{(\theta)} = \cos{(\theta + \Delta{\theta})} </math>: | |||
<center> | |||
<math> | |||
\frac{\sin{(\theta + \Delta{\theta})}}{\cos{(\theta + \Delta{\theta})}} - \frac{\sin{(\theta)}}{\cos{(\theta)}} = \frac{\Delta{x}}{\cos{(\theta)}} \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}} \to \tan{(\theta + \Delta{\theta})} - \tan{(\theta)} = \frac{\Delta{x}}{\cos{(\theta)}} \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}}. | |||
</math> | |||
</center> | |||
Considerando que o coeficiente angular da reta tangente a uma função em um dado ponto do seu domínio é igual à derivada da função nesse ponto, temos: | |||
<center> | |||
<math> | |||
\frac{\partial{y}}{\partial{x}} (x + \Delta{x}, t) - \frac{\partial{y}}{\partial{x}} (x, t) = \frac{\Delta{x}}{\cos{(\theta)}} \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}}. | |||
</math> | |||
</center> | |||
Dividindo ambos os lados por <math> \Delta{x} </math>, teremos do lado esquerdo: | |||
<center> | |||
<math> | |||
\frac{\frac{\partial{y}}{\partial{x}} (x + \Delta{x}, t) - \frac{\partial{y}}{\partial{x}} (x, t)}{\Delta{x}} | |||
</math> | |||
</center> | |||
e no limite que <math> \Delta{x} \to 0 </math>, a expressão se torna uma derivada parcial segunda <math> \frac{\partial^2{y}}{\partial{x^2}} </math>, nos permitindo reescrever a equação como: | |||
<center> | |||
<math> | |||
\frac{\partial^2{y}}{\partial{x^2}} (x, t) = \frac{1}{\cos{(\theta)}} \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}} (x, t). | |||
</math> | |||
</center> | |||
E, como última manipulação, vamos supor agora que os deslocamentos da corda são pequenos, o que implica que os ângulos associados a esses deslocamentos também são pequenos: <math> \theta << 1 </math>. Com essa condição, <math> \cos{(\theta)} \approx 1 </math> e chegamos em: | |||
<center> | |||
<math> | |||
\frac{\partial^2{y}}{\partial{x^2}} (x, t) = \frac{\mu}{T} \frac{\partial^2{y}}{\partial{t^2}} (x, t) | |||
</math> | |||
</center> | |||
onde o termo <math> \frac{\mu}{T} </math> tem dimensão de <math> \frac{1}{c^2} </math> e <math> c </math> é a velocidade de propagação de ondas na corda esticada: | |||
<center> | |||
<math> | |||
\frac{\partial^2{y}}{\partial{x^2}} (x, t) = \frac{1}{c^2} \frac{\partial^2{y}}{\partial{t^2}} (x, t) \Leftrightarrow \frac{\partial^2{y}}{\partial{t^2}} (x, t) = | |||
c^2 \frac{\partial^2{y}}{\partial{x^2}} (x, t) \Leftrightarrow y_{tt} = c^2 y_{xx}. | |||
</math> | |||
</center> | |||
Chegando a conlusão de que essa é a expressão para a corda vibrante e que a velocidade de propagação aumenta com a tensão na corda e diminui com a sua inércia (massa por unidade de comprimento). | |||
=== Solução Analítica === | |||
Começaremos tomando as condições de contorno da corda: | |||
<center> | |||
<math> | |||
y(0,t) = 0 | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
y(L,t) = 0 | |||
</math>, | |||
</center> | |||
indicando que as extremidades da corda permanecem fixas. | |||
Além disso, tomaremos também as seguintes condições iniciais para a posição e velocidade da corda: | |||
<center> | |||
<math> | |||
y(x,0) = f(x) </math>, <math> 0 \leq x \leq L | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
\frac{\partial{y}}{\partial{t}} (x,0) = y_t = g(x) </math>, <math> 0 \leq x \leq L | |||
</math>, | |||
</center> | |||
onde <math> f(x) </math> e <math> g(x) </math> são funções tais que | |||
<center> | |||
<math> | |||
f(0) = f(L) = 0 | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
g(0) = g(L) = 0. | |||
</math> | |||
</center> | |||
Iniciaremos o estudo das vibrações em uma corda elástica admitindo que a velocidade inicial da corda é nula, ou seja: | |||
<center> | |||
<math> | |||
g(x) = 0 </math>, <math> \forall 0 \leq x \leq L. | |||
</math> | |||
</center> | |||
Em outras palavras, estamos tratando do problema: | |||
<center> | |||
<math> | |||
\begin{aligned} | |||
\begin{cases} | |||
y_{tt} = c^2 y_{xx},\\ | |||
y(0,t) = 0, \\ | |||
y(L,t) = 0,\\ | |||
y(x,0) = f(x), & 0\leq x \leq L,\\ | |||
y_t = g(x), & 0\leq x \leq L.\\ | |||
\end{cases} | |||
\end{aligned} | |||
</math> | |||
</center> | |||
Em que <math> f(0) = f(L) = 0 </math> descreve a configuração da corda no início. | |||
Usaremos o método da separação de variáveis para resolver o problema admitindo que <math> y </math> pode ser escrita como | |||
<center> | |||
<math> | |||
y(x,t) = X(x)T(t) | |||
</math> | |||
</center> | |||
na qual <math> X </math> depende apenas de <math> x </math> e <math> T </math> depende apenas de <math> t </math>. | |||
Aplicando na equação diferencial parcial, temos: | |||
<center> | |||
<math> | |||
\frac{X''}{X} = \frac{1}{c^2} \frac{T''}{T} = - \lambda, | |||
</math> | |||
</center> | |||
onde <math> \lambda </math> é uma constante de separação. | |||
Logo, obtemos | |||
<center> | |||
<math> | |||
X'' + \lambda X = 0 | |||
</math> | |||
</center> | |||
e | |||
<center> | |||
<math> | |||
T'' + c^2 \lambda T = 0 | |||
</math> | |||
</center> | |||
Aplicando as condições de contorno, encontramos o problema | |||
<center> | |||
<math> | |||
X'' + \lambda X = 0 </math>, <math> X(0) = X(L) = 0, | |||
</math> | |||
</center> | |||
cuja solução é dada por | |||
<center> | |||
<math> | |||
X_n (x) = \sin{\left(\frac{n \pi x}{L} \right)}, \ {\lambda}_n = \left(\frac{n \pi}{L} \right)^2, \ n = 1, 2, 3, ... | |||
</math> | |||
</center> | |||
Com as constantes de separação acima, podemos obter a EDO | |||
<center> | |||
<math> | |||
T'' + {\omega}^2 T = 0, \ \omega = \frac{n \pi c}{L}, | |||
</math> | |||
</center> | |||
cujas soluções são | |||
<center> | |||
<math> | |||
T(t) = k_1 \cos{(\omega t)} + k_2 \sin{(\omega t)}. | |||
</math> | |||
</center> | |||
Pelo fato da velocidade inicial da corda ser nula, deduzimos que | |||
<center> | |||
<math> | |||
y_t (x,0) = X(x)T'(0) = 0, \ \forall 0 \leq x \leq L, \ \Rightarrow T'(0) = 0. | |||
</math> | |||
</center> | |||
Como | |||
<center> | |||
<math> | |||
T'(t) = - \omega k_1 \sin{(\omega t)} + \omega k_2 \cos{(\omega t)}, | |||
</math> | |||
</center> | |||
temos | |||
<center> | |||
<math> | |||
T'(0) = 0 \ \Rightarrow k_2 = 0. | |||
</math> | |||
</center> | |||
Assim, as soluções fundamentais da equação da onda, envolvendo as condições de contorno e a segunda condição inicial são dadas por: | |||
<center> | |||
<math> | |||
y_n (x,t) = \sin{\left(\frac{n \pi x}{L} \right)} \cos{(\omega t)} = \sin{\left(\frac{n \pi x}{L} \right)} \cos{\left(\frac{n \pi c t}{L} \right)}, | |||
</math> | |||
</center> | |||
para <math> n = 1, 2, 3, ... </math> <ref name="y_periodica"/>. | |||
Por fim, a superposição das soluções fundamentais nos fornece | |||
<center> | |||
<math> | |||
y(x,t) = \sum^{\infty}_{n=1} c_n \sin{\left(\frac{n \pi x}{L} \right)} \cos{\left(\frac{n \pi c t}{L} \right)} | |||
</math> | |||
</center> | |||
e a condição inicial <math> y(x,0) = f(x) </math> fornece | |||
<center> | |||
<math> | |||
y(x,0) = \sum^{\infty}_{n=1} c_n \sin{\left(\frac{n \pi x}{L} \right)} = f(x). | |||
</math> | |||
</center> | |||
Então, admitindo que <math> f(x) </math> é uma função ímpar com período <math> T = 2L </math>, concluímos que os coeficientes satisfazem | |||
<center> | |||
<math> | |||
c_n = \frac{2}{L} \int^{L}_{0} f(x) \sin{\left(\frac{n \pi x}{L} \right)} dx, \ n = 1, 2, 3, ... | |||
</math> | |||
</center> | |||
Juntando as informações, temos que a solução do problema | |||
<center> | |||
<math> | |||
\begin{aligned} | |||
\begin{cases} | |||
y_{tt} = c^2 y_{xx},\\ | |||
y(0,t) = 0, \\ | |||
y(L,t) = 0,\\ | |||
y(x,0) = f(x), & 0\leq x \leq L,\\ | |||
y_t = g(x), & 0\leq x \leq L.\\ | |||
\end{cases} | |||
\end{aligned} | |||
</math> | |||
</center> | |||
é dada por | |||
<center> | |||
<math> | |||
y(x,t) = \sum^{\infty}_{n=1} c_n \sin{\left(\frac{n \pi x}{L} \right)} \cos{\left(\frac{n \pi c t}{L} \right)}, | |||
</math> | |||
<ref name="freq_nat"/> | |||
</center> | |||
em que | |||
<center> | |||
<math> | |||
c_n = \frac{2}{L} \int^{L}_{0} f(x) \sin{\left(\frac{n \pi x}{L} \right)} dx, \ n = 1, 2, 3, ... | |||
</math> | |||
</center> | |||
=== Adaptação da equação da onda para uma corda real === | |||
Até o presente momento, tudo que foi apresentado diz respeito a uma corda ideal. Como é de se esperar, cordas reais terão algumas perdas por atrito (amortecimento) e também uma rigidez. Para termos ideia de como se dá esse comportamento real, adicionaremos esses novos dois termos na composição da nossa equação da onda: | |||
<center> | |||
<math> | |||
\frac{\partial^2 y}{\partial t^2} = c^{2}\left ( \frac{\partial^2 y}{\partial x^2} - \epsilon L^{2}\frac{\partial^4 y}{\partial x^4} \right ) - 2b\frac{\partial y}{\partial t} \Leftrightarrow y_{tt} = c^2 (y_{xx} - \epsilon L^2 y_{xxxx}) - 2b y_t, | |||
</math> | |||
</center> | |||
onde o termo da derivada de 4ª ordem vem da rigidez da corda, o qual é controlado por <math> \epsilon </math>, <math> L </math> é o comprimento da corda e <math> -2b y_t </math> é o amortecimento sofrido pela corda ao longo do tempo de propagação da onda. | |||
Utilizaremos essa equação futuramente para compreensão visual do comportamento de uma corda mais próxima da realidade. | |||
== Método FTCS == | == Método FTCS == | ||
=== | O método FTCS (Forward Time Central Space) é uma abordagem progressiva no tempo e centrada no espaço. Em outras palavras, ao lidarmos com uma função de duas variáveis, buscamos uma solução futura em termos do tempo, centrada em uma vizinhança espacial. Para a resolução numérica da equação diferencial unidimensional da onda, optamos por trabalhar exclusivamente com o método explícito. | ||
=== Corda Ideal === | |||
==== Método Explícito ==== | |||
Para aplicar o método, é necessário inicialmente discretizar tanto as variáveis espaciais quanto as variáveis temporais. Seja a função <math> y(t,x): \mathbb{R}^{2} \mapsto \mathbb{R} </math>, sejam os intervalos <math> \left [ 0,X \right ], \left [ 0,T \right ]\subset \mathbb{R} </math> e <math> N,M\in \mathbb{N} </math>, discretizamos os intervalos em espaçamentos iguais <math> \Delta x = X/N </math>, <math> \Delta t = T/M </math> de tal maneira que obtemos as sequências crescentes monótonas <math>\left \{ x_{j} \right \}_{j=0}^{N} </math> e <math>\left \{ t_{i} \right \}_{i=0}^{M} </math> . Assim obtemos uma grade de malhas de pontos <math> (t_{n}, x_{j}) </math> onde a função <math> y(t,x) </math> tem seus valores aproximados por <math> y(t_{n}, x_{j}) </math> denotado <math> y_{j}^{n} </math>. Uma abordagem comum envolve a discretização da primeira derivada no tempo utilizando uma diferença finita progressiva baseada na expansão em séries de Taylor até a primeira ordem : | |||
<center> | |||
<math> | |||
\frac{\partial y}{\partial t} \approx \frac{y(t+\Delta t, x) - y(t, x)}{\Delta t} = \frac{y_{j}^{n+1} - y_{j}^{n}}{\Delta t} | |||
</math> | |||
</center> | |||
Discretizando a derivada temporal segunda utilizando um diferença finita regressiva : | |||
<center> | |||
<math> | |||
\frac{\partial^2 y}{\partial t^2} \approx \frac{\partial}{\partial t} \left(\frac{y_{j}^{n+1} - y_{j}^{n}}{\Delta t}\right) \approx \frac{1}{\Delta t}\left [\frac{y\left (t+\Delta t, x \right ) - y\left (\left (t + \Delta t \right )- \Delta t, x \right )}{\Delta t} - \frac{y\left (t,x \right ) - y\left (t - \Delta t, x \right )}{\Delta t } \right ] = \frac{y\left (t + \Delta t, x \right ) + y\left (t - \Delta t, x \right ) - 2y\left (t, x \right )}{(\Delta t)^{2}} = \frac{y_{j}^{n+1} + y_{j}^{n-1} - 2y_{j}^{n}}{(\Delta t)^{2}} | |||
</math> | |||
</center> | |||
note que o processo retorna uma derivada de diferenças finitas centrada, além disso obtemos um aproximação de segunda ordem. O mecanismo de discretização das derivadas espaciais é completamente análogo, a derivada segunda centrada : | |||
<center> | |||
<math> | |||
\frac{\partial^{2} y}{\partial x^{2}} \approx \frac{y_{j+1}^{n} + y_{j-1}^{n} - 2y_{j}^{n}}{(\Delta x)^{2}} | |||
</math> | |||
</center> | |||
Aplicando as expressões das diferenciais na equação da onda : | |||
<center> | |||
<math> | |||
\frac{\partial^2 y}{\partial t^2} = c^{2} \frac{\partial^2 y}{\partial x^2} \mapsto \frac{y_{j}^{n+1} + y_{j}^{n-1} - 2y_{j}^{n}}{(\Delta t)^{2}} = c^{2}\frac{y_{j+1}^{n} + y_{j-1}^{n} - 2y_{j}^{n}}{(\Delta x)^{2}} | |||
</math> | |||
</center> | |||
defina <math> a := c\Delta t / \Delta x </math> e explicite a variável no estado temporal futuro, obtemos : | |||
<center> | |||
<math> | |||
y_{j}^{n+1} = 2\left(1 - a^{2}\right)y_{j}^{n} - y_{j}^{n-1} + a^{2}\left ( y_{j+1}^{n} + y_{j-1}^{n}\right ) | |||
</math> | |||
</center> | |||
uma equação explicita no tempo <math> n+1 </math> dependendo somente de <math> n </math> e <math> n-1 </math>. | |||
==== Estabilidade ==== | |||
Para analisar a estabilidade da solução numérica para a equação da onda, utilizaremos o método de Von Neumann. O procedimento consiste em utilizar a transformada de Fourier para determinar a estabilidade do esquema, a solução problema tem a forma : | |||
<center> | |||
<math> | |||
y_{j}^{n+1}(\xi) = A(\xi \Delta x, \Delta x, \Delta t) y_{j}^{n}(\xi) | |||
</math> | |||
</center> | |||
onde <math> \xi \in \left [ -\pi / \Delta x, \pi / \Delta x \right ] </math> e <math> A </math> é o fator de amplificação, observe que podemos estudar a estabilidade da aproximação somente analisando o fator de amplificação. | |||
*'''Teorema''' : Se o fator de amplificação não depender de <math> \Delta x </math> nem <math> \Delta t </math>, então a aproximação é estável se <math> \left | A(\xi \Delta x) \right | \leq 1 </math>. | |||
Vejamos a estabilidade da aproximação de diferenças finitas para a equação da onda, utilizando as componentes de Fourier <math >y_{j}^{n} \mapsto B^{n}e^{ikj\Delta x} </math>, obtemos : | |||
<center> | |||
<math> | |||
B^{n+1}e^{ikj\Delta x} = 2\left ( 1-a^{2} \right )B^{n}e^{ikj\Delta x} - B^{n-1}e^{ikj\Delta x} + a^{2}\left ( B^{n}e^{ik(j+1)\Delta x} + B^{n}e^{ik(j-1)\Delta x} \right ) | |||
</math> | |||
</center> | |||
simplificando os termos em comum : | |||
<center> | |||
<math> | |||
B^{n+1} + B^{n-1} = B^{n} \left [ 2\left ( 1-a^{2} \right ) + a^{2}\left (e^{ik\Delta x} + e^{-ik\Delta x}\right )\right ] | |||
</math> | |||
</center> | |||
note que <math> e^{ik\Delta x} - e^{-ik\Delta x} = 2cos(k\Delta x) </math>, | |||
<center> | |||
<math> | |||
\frac{B^{n+1} + B^{n-1}}{B^{n}} = 2\left ( 1-a^{2} \right ) + 2a^{2}cos(k\Delta x) | |||
</math> | |||
</center> | |||
utilizando a identidade trigonométrica <math> cos(\theta) = cos^{2}(\theta /2) - sen^{2}(\theta /2) </math> e a identidade trigonométrica fundamental <math> 1 = cos^{2}(\theta) + sen^{2}(\theta) </math>, obtemos : | |||
<center> | |||
<math> | |||
A + \frac{1}{A} = -2\left [ 2a^{2}sen^{2}\left ( \frac{k\Delta x}{2} \right ) -1 \right ] | |||
</math> | |||
</center> | |||
onde <math> A = B^{n+1}/B^{n} </math> <ref name="fator_ampl"/> é o fator de amplificação. Defina <math> d := 2a^{2}sen^{2}\left (k\Delta x / 2 \right ) -1 </math>. Portanto obtemos a equação quadrática com soluções : | |||
<center> | |||
<math> | |||
A^{2} + 2dA + 1 = 0 \Rightarrow A_{1,2} = -d \pm \sqrt{d^{2}-1} | |||
</math> | |||
</center> | |||
se <math> \left | d \right | > 1 </math>, então : | |||
<center> | |||
<math> | |||
-1>d>1 \Rightarrow -1 > 2a^{2}sen^{2}\left (k\Delta x / 2 \right ) -1 > 1 \Rightarrow 0 > 2a^{2}sen^{2}\left (k\Delta x / 2 \right ) > 2 \Rightarrow 0 > \left( asen\left (k\Delta x / 2 \right ) \right)^{2} > 1 | |||
</math> | |||
</center> | |||
o que é um aburdo, pois <math> asen\left (k\Delta x / 2 \right )\in \mathbb{R} </math>. Se <math> \left | d \right | \leq 1 </math> , então : | |||
<center> | |||
<math> | |||
-1\leq d \leq 1 \Rightarrow -1 \leq 2a^{2}sen^{2}\left (k\Delta x / 2 \right ) -1 \leq 1 \Rightarrow 0 \leq 2a^{2}sen^{2}\left (k\Delta x / 2 \right ) \leq 2 \Rightarrow 0 \leq \left( asen\left (k\Delta x / 2 \right ) \right)^{2} \leq 1 | |||
</math> | |||
</center> | |||
note que <math> sen\left (k\Delta x / 2 \right ) \leq 1 </math>, logo <math> a \leq 1 </math>. Portanto para o método ser condicionalmente estável : | |||
<center> | |||
<math> | |||
\frac{c \Delta t}{ \Delta x} \leq 1 | |||
</math> | |||
</center> | |||
Embora <math> a \leq 1 </math> garante a estabilidade do processo, <math> a = 1 </math> é a melhor escolha possível para a estabilidade do método, pelos seguintes motivos : | |||
* Quando <math> a = 1 </math>, os termos de ordem superior que são descartados na discretização da equação da onda são amplamente cancelados. Essa compensação implica que o método numérico se torna mais estável e menos suscetível a erros numéricos significativos, ou seja, não ocorrerão variações abruptas devido aos termos de ordem maiores; | |||
* Quando <math> a = 1 </math>, a perturbação na corda se propaga exatamente um passo espacial a cada passo de tempo. Esse comportamento assegura que a velocidade da perturbação seja adequadamente representada pelo algoritmo numérico. Isso ocorre devido a relação entre a velocidade física da corda <math> c </math> e a velocidade da perturbação <math> v = \Delta x / \Delta t </math>. A animação abaixo contém soluções da equação da onda ideal, obtidas utilizando o método FTCS com diferentes a's. Nela fica bem claro que a velocidade de propagação das ondas na solução para <math>a=0,5</math> é metade da solução para <math>a=1</math> | |||
[[Arquivo:Different_ks.gif|frame|center|Soluções obtidas para a equação da onda ideal com diferentes a's.]] | |||
<center> | |||
<math> | |||
\frac{c \Delta t}{ \Delta x} = \frac{c}{v} | |||
</math> | |||
</center> | |||
Observe que além de obtermos o intervalo de estabilidade <math> a\in\left [ 0, 1 \right ] </math>, também obtemos uma restrição na discretização das malhas temporais e espaciais, limitando assim <math> N,M\in \mathbb{N} </math> a um subconjunto que satisfaça a condição de estabilidade. | |||
=== Corda Não Ideal === | |||
==== Método Explícito ==== | |||
Optaremos novamente por realizar a análise utilizando um método explícito. Em geral, o desenvolvimento teórico para a discretização da equação diferencial da onda com amortecimento e rigidez é análogo ao caso ideal, portanto, não serão apresentados com detalhes os cálculos necessários para a implementação do método. A derivada quarta centrada é aproximada utilizando diferenças finitas : | |||
<center> | |||
<math> | |||
\frac{\partial^4 y}{\partial x^4} \approx \frac{y_{j+2}^{n} + y_{j+1}^{n} + y_{j}^{n} + y_{j-1}^{n} + y_{j-2}^{n}}{\left ( \Delta x \right )^{4}} | |||
</math> | |||
</center> | |||
transformando a EDP não homogênea para um espaço discretizado usando a aproximação de diferenças finitas centrada : | |||
<center> | |||
<math> | |||
\frac{\partial^2 y}{\partial t^2} = c^{2}\left ( \frac{\partial^2 y}{\partial x^2} - \epsilon L^{2}\frac{\partial^4 y}{\partial x^4} \right ) - 2b\frac{\partial y}{\partial t} \mapsto y_{j}^{n+1} = \left [ \left (2 - 2a^{2} - 6\epsilon a^{2}E^{2} - F \right )y_{j}^{n} - y_{j}^{n-1} + a^{2}\left ( 1 + 4\epsilon E^{2} \right ) \left ( y_{j+1}^{n} + y_{j-1}^{n} \right ) - \epsilon a^{2}E^{2} \left ( y_{j+2}^{n} + y_{j-2}^{n} \right ) \right ]\left (\frac{1}{1-F} \right ) | |||
</math> | |||
</center> | |||
onde <math> E := L/ \Delta x </math> e <math> F := b/ \Delta t </math>. Novamente obtemos um equação explicita no tempo <math> n+1 </math> que depende somente de <math> n </math> e <math> n-1 </math>; | |||
==== Estabilidade ==== | |||
A abordagem que empregamos para demonstrar a estabilidade da equação da onda não homogênea é completamente análoga ao caso homogêneo. Em outras palavras, utilizamos o método de Von Neumann em conjunto com o teorema da estabilidade. Ao aplicar novamente as componentes de Fourier, representadas por <math >y_{j}^{n} \mapsto B^{n}e^{ikj\Delta x} </math>, obtemos uma equação quadrática que impõe a seguinte restrição : | |||
<center> | |||
<math> | |||
a = \frac{c \Delta t}{ \Delta x} \leq \frac{1}{4} | |||
</math> | |||
</center> | |||
logo, o método é condicionalmente estável no intervalo <math> a\in\left [ 0, 1/4 \right ] </math>. | |||
=== Convergência, Consistência e Estabilidade === | |||
Até este ponto, ainda não discutimos o quão bem o esquema de diferenças finitas descreve a solução da equação diferencial. Vamos abordar isso agora. A propriedade mais essencial que um esquema deve possuir é que, à medida que os espaçamentos na malha discreta diminuem, a aproximação para a solução deve se aproximar da solução real do sistema. Portanto, um esquema é considerado uma boa aproximação se | |||
<center> | |||
<math> | |||
\left ( \Delta t, \Delta x \right ) \rightarrow 0 \Rightarrow \left | y \left ( t_{n}, x_{j}\right ) - y_{j}^{n} \right |\rightarrow 0 | |||
</math> | |||
</center> | |||
onde <math> y \left ( t_{n}, x_{j}\right ) </math> é a solução exata e <math> y_{j}^{n} </math> a solução aproximada. Se tais condições são satisfeitas, dizemos que o esquema de equações diferenciais finitas é convergente. Entretanto, geralmente, provar a convergência não é uma tarefa trivial. No entanto, podemos demonstrá-la de maneira indireta, utilizando estabilidade e consistência. Se um esquema é estável e consistente, então a convergência do esquema é garantida. Dada uma equação diferencial <math> Dy = f </math>, dizemos que o esquema de diferenças finitas <math> D_{\Delta t \Delta x}y = f </math> é consistente com a equação diferencial se, para qualquer função suficientemente diferenciável <math> \phi(t, x) </math>, | |||
<center> | |||
<math> | |||
\left ( \Delta t, \Delta x \right ) \rightarrow 0 \Rightarrow D \phi - D_{\Delta t \Delta x} \phi \rightarrow 0 | |||
</math> | |||
</center> | |||
Mostremos a consistência da aproximação de diferenças finitas para a equação da onda homogênea. Seja a EDP da onda | |||
<center> | |||
<math> | |||
Dy\left ( t, x \right ) = \frac{\partial^2 y}{\partial t^2} - c^{2}\frac{\partial^2 y}{\partial x^2} | |||
</math> | |||
</center> | |||
e seja a equação de diferenças finitas | |||
<center> | |||
<math> | |||
D_{\left (\Delta t \Delta x \right )}y\left ( t, x \right ) = \frac{y_{j}^{n+1} + y_{j}^{n-1} - 2y_{j}^{n}}{(\Delta t)^{2}} - c^{2}\frac{y_{j+1}^{n} + y_{j-1}^{n} - 2y_{j}^{n}}{(\Delta x)^{2}} | |||
</math> | |||
</center> | |||
pela aproximação que demonstramos anteriormente, temos : | |||
<center> | |||
<math> | |||
\begin{aligned} | |||
&\frac{\partial^2 y}{\partial t^2} - c^{2}\frac{\partial^2 y}{\partial x^2} = \frac{y_{j}^{n+1} + y_{j}^{n-1} - 2y_{j}^{n}}{(\Delta t)^{2}} + O\left ( \Delta t^{2} \right )- c^{2}\frac{y_{j+1}^{n} + y_{j-1}^{n} - 2y_{j}^{n}}{(\Delta x)^{2}} + O\left ( \Delta x^{2} \right ) \\ | |||
&\frac{\partial^2 y}{\partial t^2} - c^{2}\frac{\partial^2 y}{\partial x^2} - \left (\frac{y_{j}^{n+1} + y_{j}^{n-1} - 2y_{j}^{n}}{(\Delta t)^{2}} - c^{2}\frac{y_{j+1}^{n} + y_{j-1}^{n} - 2y_{j}^{n}}{(\Delta x)^{2}} \right ) = O\left ( \Delta t^{2} \right ) + O\left ( \Delta x^{2} \right ) \\ | |||
&Dy\left ( t, x \right ) - D_{\left (\Delta t \Delta x \right )}y\left ( t, x \right ) = O\left ( \Delta t^{2} \right ) + O\left ( \Delta x^{2} \right ) | |||
\end{aligned} | |||
</math> | |||
</center> | |||
como estamos supondo que os termos de ordem 2 são desprezíveis, <math> O\left ( \Delta t^{2} \right ) \rightarrow 0 </math> e <math> O\left ( \Delta x^{2} \right ) \rightarrow 0 </math>. Logo : | |||
<center> | |||
<math> | |||
Dy\left ( t, x \right ) - D_{\left (\Delta t \Delta x \right )}y\left ( t, x \right ) \rightarrow 0 | |||
</math> | |||
</center> | |||
portanto o esquema de diferenças finitas é consistente. Como na seção anterior já havíamos provado a estabilidade condicional do método, podemos concluir que o esquema é condicionalmente convergente (é consistente e condicionalmente estável) e portanto representa uma boa aproximação para a solução exata da equação diferencial. | |||
== Análise espectral == | == Análise espectral == | ||
| Linha 9: | Linha 613: | ||
=== Supremacia da álgebra linear === | === Supremacia da álgebra linear === | ||
O seguinte conjunto <math> \mathbb{R}^{\mathbb{R}} = \{ f~|~f: \mathbb{R} \to \mathbb{R} \} </math> é o espaço de funções reais de uma variável. Esse conjunto é um espaço vetorial, logo podemos utilizar toda a artilharia da álgebra linear, em especial, estamos interessados no sub-espaço gerado pela base <math> B = \{sen(\omega t) / \sqrt{ | O seguinte conjunto <math> \mathbb{R}^{\mathbb{R}} = \{ f~|~f: \mathbb{R} \to \mathbb{R} \} </math> é o espaço de funções reais de uma variável. Esse conjunto é um espaço vetorial, logo podemos utilizar toda a artilharia da álgebra linear, em especial, estamos interessados no sub-espaço gerado pela base <math> B = \{sen(\omega t) / \sqrt{\pi}, cos(\omega t) / \sqrt{\pi} \}_{\omega \in \mathbb{R^+}} </math> <ref name="norm_const"/>, pois elementos de <math> B </math>, interpretados como sinais sonoros, representam um frequência pura de valor <math>f=\omega/(2\pi)</math>. Dessa forma, um sinal arbitrário <math>s(t)</math> pode ser escrito em termos das frequências puras que o formam | ||
<center> | |||
<math> | <math> | ||
s(t) = \frac{1}{\sqrt{ | s(t) = \frac{1}{\sqrt{\pi}}\int_{0}^{\infty}[a(\omega)cos(\omega t) + b(\omega)sen(\omega t]d\omega | ||
</math> | </math> | ||
</center> | |||
E podemos extrair suas coordenadas (conhecidas como transformada de Fourier do sinal) (<math>a(\omega)</math> e <math>b(\omega)</math>), fazendo o produto escalar com os elementos da base | |||
<center> | |||
<math> | |||
\begin{aligned} | |||
a(\omega) &= \int_{-\infty}^{\infty}s(t)\frac{1}{\sqrt{\pi}}cos(\omega t)dt \\ | |||
b(\omega) &= \int_{-\infty}^{\infty}s(t)\frac{1}{\sqrt{\pi}}sen(\omega t)dt | |||
\end{aligned} | |||
</math> | |||
</center> | |||
Se o domínio de <math>s(t)</math> é limitado, digamos <math>t \in [0, T]</math>, então uma base infinita com cardinalidade enumerável (em contraste com a base anterior, que possui cardinalidade não enumerável) é suficiente para representar <math>s(t)</math>, uma possível base ortonormal é a seguinte: <math>\bigg\{ \sqrt{\frac{1}{T}}, \sqrt{\frac{2}{T}}sen(\omega_n t), \sqrt{\frac{2}{T}}cos(\omega_n t) \bigg\}_{n \in \mathbb{N^*}}</math>, em que <math> \omega_n = \frac{n\pi}{T} </math>. Dessa forma, a representação e coordenadas de <math>s(t)</math> ficam | |||
<center> | |||
<math> | <math> | ||
\begin{aligned} | \begin{aligned} | ||
s(t) &= a_0\sqrt{\frac{1}{T}} + \sqrt{\frac{2}{T}}\sum_{n=1}^{\infty}\bigg[a_n cos(\omega_n t) + b_n sen(\omega_n) \bigg] \\ | |||
a_0 &= \int_0^T s(t) \sqrt{\frac{1}{T}}dt \\ | |||
a_n &= \int_0^T s(t) \sqrt{\frac{2}{T}}cos(\omega_n t)dt \\ | |||
b_n &= \int_0^T s(t) \sqrt{\frac{2}{T}}sen(\omega_n t)dt \\ | |||
\end{aligned} | |||
</math> | |||
</center> | |||
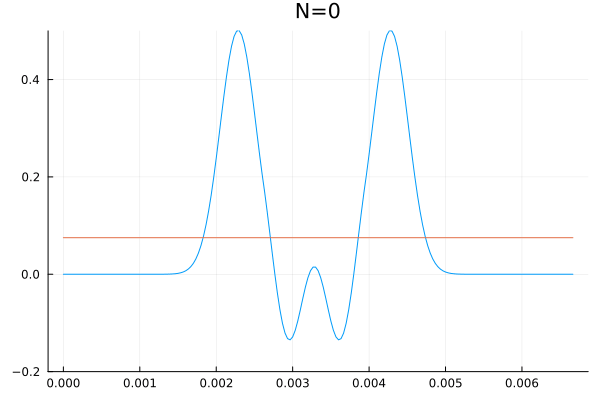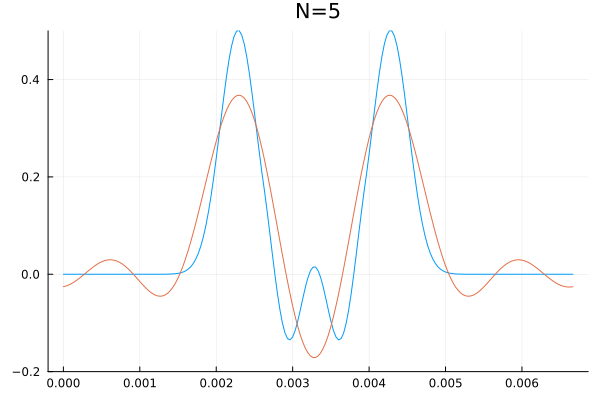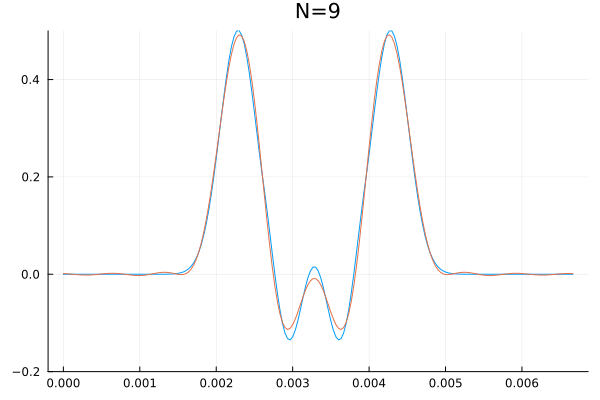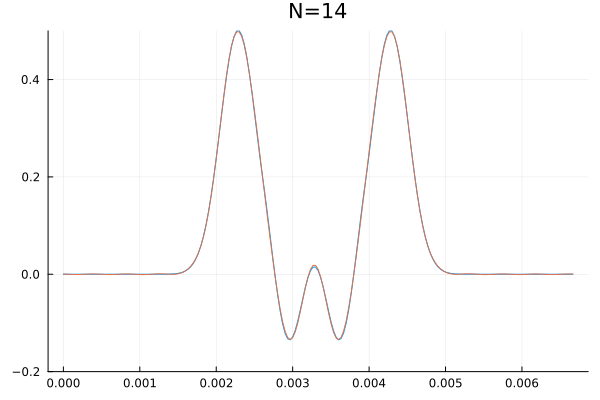
É impossível falar sobre bases enumeráveis de um sub-espaço de <math> \mathbb{R}^{\mathbb{R}} </math> sem representar esse canhão matemático com uma animação. Abaixo segue uma visualização que calcula as primeiras <math>N</math> coordenadas (<math>a_0,\dots,a_N</math> e <math>b_1,\dots,b_N</math>) de um sinal qualquer e sobrepõem a série obtida, incrementando <math>N</math> até as duas curvas serem indistinguíveis a olho nu. | |||
<center> | |||
[[Arquivo:Serie_fourier_ana_julia.gif|frame|center|Animação de uma série de fourier. É interessante notar que a série converge muito bem com apenas uma dúzia de frequências.]] | |||
</center> | |||
=== Potência espectral === | |||
Adiante vamos ver que o sinal sonoro provém da vibração de um ponto específico da mesma, digamos em <math>x=x_o</math>, então a função que representa o sinal é <math>y(x_o, t)</math>. Como estamos interessados nas frequências que compõem o sinal, será calculado a transformada de fourier de <math>y(x_o, t)</math> e definido que a potência da frequência <math>f = \omega/(2\pi)</math> é <math>a_\omega^2 + b_\omega^2</math>. A potência em função da frequência é o resultado da análise espectral. | |||
== Simulando uma corda de violão == | |||
Uma corda de violão geralmente é excitada por uma pancada dada por uma palheta ou pelo próprio dedo/unha do violonista. Essa pancada define uma condição inicial para a equação de onda. Uma suposição razoável da condição gerada é a seguinte | |||
<math> | |||
\begin{aligned} | |||
y(x, t=0) &= \begin{cases} | |||
\frac{h}{x_0}x &, ~ 0 \leq x \leq x_0\\ | |||
\frac{h}{L-x_0}(-x + L) &, ~ x_0 \leq x \leq L\\ | |||
\end{cases} \\ | |||
\frac{\partial}{\partial t} y(x, t=0) &= 0 | |||
\end{aligned} | \end{aligned} | ||
</math> | </math> | ||
supondo que a corda possui comprimento <math>L</math> e a pancado ocorreu em <math>x_o</math>, causando uma deslocamento máximo <math>h</math>. A imagem a seguir ilustra o estado da corda logo após a excitação | |||
= | <center> | ||
[[Arquivo:Init_cond_ana_julia.png|thumb|upright=2|center|Condição inicial de uma corda de violão.]] | |||
</center> | |||
Dado essa condição inicial, podemos evoluir temporalmente o estado da corda utilizando a equação da onda, mantendo as bordas fixas (<math>y(x=0, t) = y(x=L, t) = 0</math>), mas como extrair som dessa simulação? Para responder essa pergunta precisamos saber como um violão gera som. Ao contrário do que inicialmente pareça, as ondas sonoras não são diretamente geradas pela vibração das cordas, mas sim da caixa do violão, que está diretamente conectada com as cordas em uma peça chamada ponte. A vibração das cordas gera uma força dependente do tempo que atua na caixa através da ponte, assim vibrando a caixa e gerando o som que escutamos. Portanto, para gerar som de forma realista, precisaríamos fisicamente simular a caixa, levando em consideração a sua geometria e as propriedades física do seu material, e então determinar as ondas de pressão que seriam geradas por essa vibração, o que está fora do escopo do presente trabalho. Felizmente, as seguintes simplificações vão nos permitir calcular as ondas de pressão: | |||
* A força que a ponte exerce na caixa é aproximadamente proporcional a sua velocidade (Dinâmica aristotélica). | |||
* A onda de pressão produzida pela caixa é aproximadamente proporcional a sua velocidade. | |||
A força que a ponte exerce na caixa (<math>F(t)</math>) é a força que a corda exerce na ponte (pois a ponte está firmemente conectada na caixa), e essa força é proporcional a inclinação da corda, ou seja | |||
<center> | |||
<math> | |||
F(t) = T \frac{\partial}{\partial x}y(x=0, t) \approx T\frac{y(\Delta x, t) - \overbrace{y(0, t)}^{0}}{\Delta x} = \frac{T}{\Delta x} y(\Delta x, t) | |||
</math> | |||
</center> | |||
em que <math>T</math> é a tensão na corda. Portando, o sinal da onda de pressão pode ser aproximado como o deslocamento de um ponto da corda próximo a ponte. Para gerar som com esse sinal, o tipo de arquivo [https://en.wikipedia.org/wiki/WAV#:~:text=Waveform%20Audio%20File%20Format%20(WAVE,1991%20by%20IBM%20and%20Microsoft. WAV]] é utilizado, pois o seu dado de entrada pode ser justante o sinal da onda de pressão. | |||
Agora tudo está pronto para fazermos uma simulação, vamos tentar reproduzir a nota lá (<math>f = 440~Hz</math>). Primeiro precisamos descobrir qual deve ser a velocidade de propagação das ondas (<math>c</math>) para gerar a nota em questão. Resolvendo a equação da onda ideal, obtemos que as possíveis frequência que existem na solução são <math>f_n = \frac{nc}{2L} </math>, então não é possível fazer a corda vibrar apenas com uma frequência, mas quando músicos se referem a uma nota, eles realmente estão se referindo a <math>f_1</math>, a primeira frequência que compõem o sinal, portanto | |||
<center> | |||
<math> f_1 = \frac{c}{2L} = 440~Hz \Rightarrow c = L \cdot 880~Hz</math> | |||
</center> | |||
Assumindo <math>L=1~m</math>, temos que <math>c = 880~m/s</math>. Resolvendo a equação da onda realista pelo método FTCS com os seguinte parâmetros | |||
{| class="wikitable" | |||
|+ Parâmetros da condição inicial | |||
|- | |||
! Parâmetros !! Valor | |||
|- | |||
| <math>x_o</math> || <math>0,5~L</math> | |||
|- | |||
| h || 1 cm | |||
|} | |||
{| class="wikitable" | |||
|+ Parâmetros da integração | |||
|- | |||
! Parâmetros !! Valor | |||
|- | |||
| k || 1/4 | |||
|- | |||
| c || 880 m/s | |||
|- | |||
| <math>\Delta x</math> || 0,01 m | |||
|- | |||
| L || 1 m | |||
|- | |||
| b || 5 <math>s^{-1}</math> | |||
|- | |||
| <math>\epsilon</math> || <math>10^{-9}</math> | |||
|} | |||
obtemos o seguinte resultado | |||
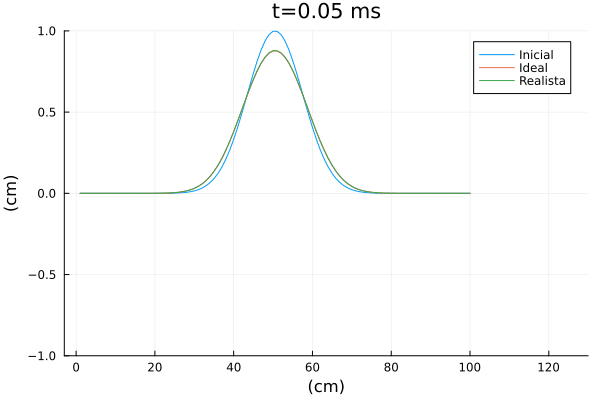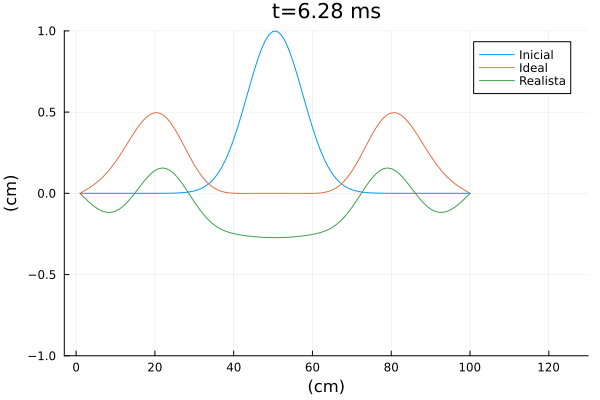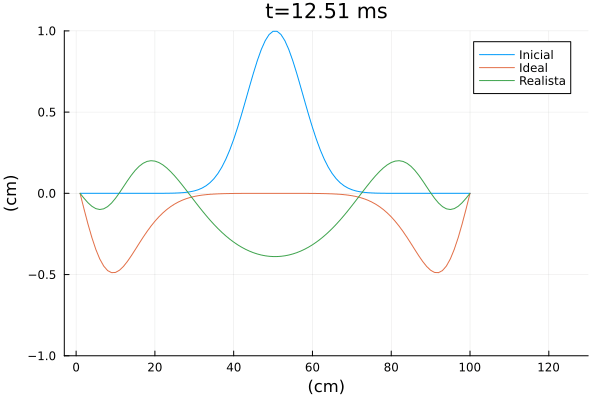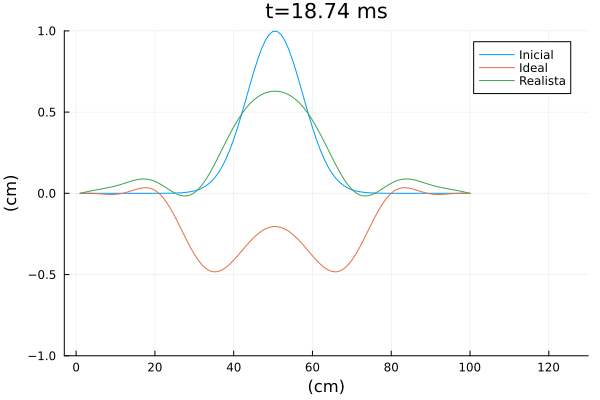
[[Arquivo:Corda_vibrando_ana_julia.gif|frame|center|Solução da equação de onda ideal e realista.]] | |||
Na animação acima, por questão de comparação, também foi coloca a solução de uma simulação com os mesmos parâmetros, apenas com a modificação <math>b=\epsilon=0</math>, que seria o caso ideal (sem amortecimento e rigidez). | |||
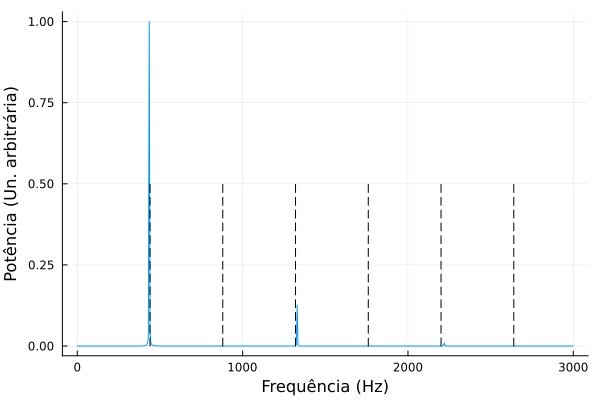
Realizando a análise espectral do deslocamento de um ponto próximo de <math>x=0</math>, obtemos o seguinte gráfico | |||
<center> | |||
[[Arquivo:La_power_ana_julia.png |thumb|upright=2|center|Espectro do deslocamento de um ponto próximo de <math>x=0</math>. Linhas pretas tracejadas representam os harmônicos.]] | |||
</center> | |||
As linhas verticais pretas e tracejadas representam as possíveis frequências da solução do caso ideal (também chamadas de harmônicos), ou seja, a primeira linha está em <math>f = 440 Hz </math> como era de se esperar, mas é notável que a segunda e quarta linhas possuem uma potência praticamente nula, isso ocorre porque a excitação inicial foi exatamente no meio, e as frequência correspondentes a essas linhas provém de ondas estacionário que possum um nodo em <math>x=L/2</math>, logo elas não foram excitadas pela condição inicial. Mudando o ponto de excitação inicial, podemos ver essas frequências aparecendo. Rodando a simulação novamente, mas com <math>x_o = 0,2~L</math>, obtemos o seguinte espectro | |||
<center> | |||
[[Arquivo:La_power_bridge_ana_julia.png |thumb|upright=2|center|Espectro para excitação inicial em <math>x_0 = 0,2~L</math>]] | |||
</center> | |||
Para observar a influência da rigidez, a simulação foi rodada com <math>\epsilon=10^{-8}</math> (10 vezes maior do que o valor anterior) resultando no seguinte espectro | |||
<center> | |||
[[Arquivo:La_power_high_stiff_ana_julia.png |thumb|upright=2|center|Espectro para <math>\epsilon=10^{-8}</math>]] | |||
</center> | |||
O efeito mais notável é o deslocamento para esquerda das frequência em relação as frequências que compõem o sinal no caso ideal. | |||
Por fim, conforme descrito anteriormente, podemos gerar som com as dados da simulação, mas infelizmente essa wiki não nos permite upar arquivos de áudio. No entanto, áudio das simulações discutidas aqui podem ser encontrados no repositório do projeto [https://github.com/marcos1561/ana-julia ana-julia] dentro da pasta "sound". Em especial, o efeito de deslocamento de frequências causado pela rigidez é bastante evidente escutando os áudios. | |||
=== Bônus === | |||
Apenas por diversão, segue uma animação de um pacote gaussiano como condição inicial | |||
[[Arquivo:Gaussian_package_ana_julia.gif|frame|center|Animação da solução da equação da onda com um pacote gaussiano como condição inicial.]] | |||
== Notas == | == Notas == | ||
<references> | <references> | ||
<ref name="norm_const">A constante <math> 1/\sqrt{ | |||
<ref name="fator_ampl"> Perceba que não estamos operando expoentes, mas sim usando a relação entre os índices <math> B^{n-1}/B^{n} = B^{m}/B^{m+1} = A^{-1} </math>.</ref> | |||
<ref name="norm_const">A constante <math> 1/\sqrt{\pi} </math> está presente por questão de normalização. Esse caso pode parecer um pouco estranho, dado que não é possível normalizar os cossenos e senos, pois sua integral em todo a reta não é definida, mas o que se deseja é a seguinte propriedade | |||
<math>\int_{\mathbb{R}}A_{\omega}cos(\omega t) \cdot A_{\omega'}cos(\omega' t)dt = \delta(\omega-\omega') </math> | <math>\int_{\mathbb{R}}A_{\omega}cos(\omega t) \cdot A_{\omega'}cos(\omega' t)dt = \delta(\omega-\omega') </math> | ||
que é | que é safisfeita quando <math> A_{\omega} = A_{\omega'} = 1/\sqrt{\pi}, ~ \forall \omega,\omega'</math>. | ||
</ref> | |||
<ref name="y_periodica"> Note que <math> y_n </math> é periódica no tempo com período <math> \frac{2L}{nc} </math>.</ref> | |||
<ref name="freq_nat"> As quantidades <math> \frac{n \pi c}{L} </math> são chamadas de frequências naturais da corda; o fator <math> \sin{\left(\frac{n \pi x}{L} \right)} </math> é chamado modo natural de vibração e o período de modo natural de vibração <math> \frac{2L}{n} </math> é chamado de comprimento de onda. | |||
</ref> | </ref> | ||
</references> | </references> | ||
== Referências == | |||
# Giordano, Nicholas, Nakanishin Hisao. Computacional Physics, Sencond Edition - 2006. | |||
# Strikwerda, John. Finite Diference Schemes and Partial Diferential Equations, Second Edition, SIAM - 2004. | |||
# Moraes, Alciney das Neves. Critério de Estabilidade de um Esquema Explícito em Diferenças Finitas para o Modelo de Placas de Mindlin-Timoshenko, Universidade Federal do Pará — 2019. | |||
# Grigoryan, Viktor. Finite differences for the wave equation. UC Santa Bárbara Mathematics - 2012. | |||
# Boyce, E., W. Equações Diferenciais Elementares e Problemas de Valores de Contorno, 11ª Edição - 2020. | |||
Edição atual tal como às 15h32min de 25 de abril de 2024
Grupo : Gustavo H. Guesser, Joshua L. Kipper, Marcos Pasa.
A equação da onda
No estudo das oscilações, é comum entre os físicos o emprego de modelos simples como representações "prototípicas" de certos padrões básicos observados na natureza. A eficácia desses modelos simples decorre de duas características fundamentais: a capacidade de serem compreendidos em detalhes minuciosos e a habilidade de reproduzir comportamentos semelhantes aos de situações reais e mais complexas, auxiliando na compreensão destas, pelo menos em termos qualitativos.
Quando se trata de comportamentos oscilatórios, o modelo mais comumente utilizado é o do sistema massa-mola. Por outro lado, para descrever comportamentos ondulatórios unidimensionais, o modelo simples mais difundido é o da corda vibrante.
Dedução
Consideremos uma corda esticada, como a corda de um violão, por exemplo. Suponhamos que esta corda tenha um comprimento e que suas extremidades estejam fixas nos pontos e . Além disso, vamos supor que a corda tenha uma densidade linear uniforme representada por , e que esteja sob uma tensão constante .
Assumindo que a corda realize vibrações transversais apenas na direção (embora possa ter vibrações transversais na direção , as quais vamos ignorar aqui), podemos representar a configuração da corda em qualquer instante de tempo no plano por uma função .
Vamos considerar mais algumas suposições:
I) A tensão que estica a corda é tão alta que podemos negligenciar a força gravitacional sobre ela;
II) A corda é perfeitamente elástica, ou seja, não oferece resistência a dobras;
III) Os deslocamentos da corda, que ocorrem apenas na direção , são de pequena amplitude.
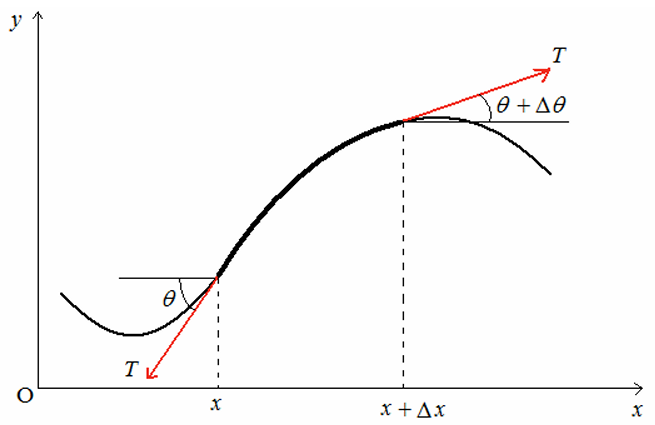
Com essas suposições em mente, estamos prontos para abordar o problema da corda vibrante. Em qualquer instante de tempo, um segmento arbitrário da corda estará na posição geral indicada pela figura abaixo:
A massa do pequeno segmento de corda de comprimento é
As componentes horizontal e vertical da força resultante atuando sobre esse segmento são:
e
Estamos assumindo que a corda não se move na direção (apenas na direção ). Isso implica que a força resultante na direção é nula (). Substituindo essa condição na equação, obtemos:
E a força resultante na direção , , é dada de acordo com a segunda lei de Newton:
então:
ou
Vamos prosseguir dividindo os dois lados da equação acima pelo termo , sabendo que :
Considerando que o coeficiente angular da reta tangente a uma função em um dado ponto do seu domínio é igual à derivada da função nesse ponto, temos:
Dividindo ambos os lados por , teremos do lado esquerdo:
e no limite que , a expressão se torna uma derivada parcial segunda , nos permitindo reescrever a equação como:
E, como última manipulação, vamos supor agora que os deslocamentos da corda são pequenos, o que implica que os ângulos associados a esses deslocamentos também são pequenos: . Com essa condição, e chegamos em:
onde o termo tem dimensão de e é a velocidade de propagação de ondas na corda esticada:
Chegando a conlusão de que essa é a expressão para a corda vibrante e que a velocidade de propagação aumenta com a tensão na corda e diminui com a sua inércia (massa por unidade de comprimento).
Solução Analítica
Começaremos tomando as condições de contorno da corda:
e
,
indicando que as extremidades da corda permanecem fixas.
Além disso, tomaremos também as seguintes condições iniciais para a posição e velocidade da corda:
,
e
, ,
onde e são funções tais que
e
Iniciaremos o estudo das vibrações em uma corda elástica admitindo que a velocidade inicial da corda é nula, ou seja:
,
Em outras palavras, estamos tratando do problema:
Em que descreve a configuração da corda no início.
Usaremos o método da separação de variáveis para resolver o problema admitindo que pode ser escrita como
na qual depende apenas de e depende apenas de .
Aplicando na equação diferencial parcial, temos:
onde é uma constante de separação.
Logo, obtemos
e
Aplicando as condições de contorno, encontramos o problema
,
cuja solução é dada por
Com as constantes de separação acima, podemos obter a EDO
cujas soluções são
Pelo fato da velocidade inicial da corda ser nula, deduzimos que
Como
temos
Assim, as soluções fundamentais da equação da onda, envolvendo as condições de contorno e a segunda condição inicial são dadas por:
para [1].
Por fim, a superposição das soluções fundamentais nos fornece
e a condição inicial fornece
Então, admitindo que é uma função ímpar com período , concluímos que os coeficientes satisfazem
Juntando as informações, temos que a solução do problema
é dada por
em que
Adaptação da equação da onda para uma corda real
Até o presente momento, tudo que foi apresentado diz respeito a uma corda ideal. Como é de se esperar, cordas reais terão algumas perdas por atrito (amortecimento) e também uma rigidez. Para termos ideia de como se dá esse comportamento real, adicionaremos esses novos dois termos na composição da nossa equação da onda:
onde o termo da derivada de 4ª ordem vem da rigidez da corda, o qual é controlado por , é o comprimento da corda e é o amortecimento sofrido pela corda ao longo do tempo de propagação da onda.
Utilizaremos essa equação futuramente para compreensão visual do comportamento de uma corda mais próxima da realidade.
Método FTCS
O método FTCS (Forward Time Central Space) é uma abordagem progressiva no tempo e centrada no espaço. Em outras palavras, ao lidarmos com uma função de duas variáveis, buscamos uma solução futura em termos do tempo, centrada em uma vizinhança espacial. Para a resolução numérica da equação diferencial unidimensional da onda, optamos por trabalhar exclusivamente com o método explícito.
Corda Ideal
Método Explícito
Para aplicar o método, é necessário inicialmente discretizar tanto as variáveis espaciais quanto as variáveis temporais. Seja a função , sejam os intervalos e , discretizamos os intervalos em espaçamentos iguais , de tal maneira que obtemos as sequências crescentes monótonas e . Assim obtemos uma grade de malhas de pontos onde a função tem seus valores aproximados por denotado . Uma abordagem comum envolve a discretização da primeira derivada no tempo utilizando uma diferença finita progressiva baseada na expansão em séries de Taylor até a primeira ordem :
Discretizando a derivada temporal segunda utilizando um diferença finita regressiva :
note que o processo retorna uma derivada de diferenças finitas centrada, além disso obtemos um aproximação de segunda ordem. O mecanismo de discretização das derivadas espaciais é completamente análogo, a derivada segunda centrada :
Aplicando as expressões das diferenciais na equação da onda :
defina e explicite a variável no estado temporal futuro, obtemos :
uma equação explicita no tempo dependendo somente de e .
Estabilidade
Para analisar a estabilidade da solução numérica para a equação da onda, utilizaremos o método de Von Neumann. O procedimento consiste em utilizar a transformada de Fourier para determinar a estabilidade do esquema, a solução problema tem a forma :
onde e é o fator de amplificação, observe que podemos estudar a estabilidade da aproximação somente analisando o fator de amplificação.
- Teorema : Se o fator de amplificação não depender de nem , então a aproximação é estável se .
Vejamos a estabilidade da aproximação de diferenças finitas para a equação da onda, utilizando as componentes de Fourier , obtemos :
simplificando os termos em comum :
note que ,
utilizando a identidade trigonométrica e a identidade trigonométrica fundamental , obtemos :
onde [3] é o fator de amplificação. Defina . Portanto obtemos a equação quadrática com soluções :
se , então :
o que é um aburdo, pois . Se , então :
note que , logo . Portanto para o método ser condicionalmente estável :
Embora garante a estabilidade do processo, é a melhor escolha possível para a estabilidade do método, pelos seguintes motivos :
- Quando , os termos de ordem superior que são descartados na discretização da equação da onda são amplamente cancelados. Essa compensação implica que o método numérico se torna mais estável e menos suscetível a erros numéricos significativos, ou seja, não ocorrerão variações abruptas devido aos termos de ordem maiores;
- Quando , a perturbação na corda se propaga exatamente um passo espacial a cada passo de tempo. Esse comportamento assegura que a velocidade da perturbação seja adequadamente representada pelo algoritmo numérico. Isso ocorre devido a relação entre a velocidade física da corda e a velocidade da perturbação . A animação abaixo contém soluções da equação da onda ideal, obtidas utilizando o método FTCS com diferentes a's. Nela fica bem claro que a velocidade de propagação das ondas na solução para é metade da solução para
Observe que além de obtermos o intervalo de estabilidade , também obtemos uma restrição na discretização das malhas temporais e espaciais, limitando assim a um subconjunto que satisfaça a condição de estabilidade.
Corda Não Ideal
Método Explícito
Optaremos novamente por realizar a análise utilizando um método explícito. Em geral, o desenvolvimento teórico para a discretização da equação diferencial da onda com amortecimento e rigidez é análogo ao caso ideal, portanto, não serão apresentados com detalhes os cálculos necessários para a implementação do método. A derivada quarta centrada é aproximada utilizando diferenças finitas :
transformando a EDP não homogênea para um espaço discretizado usando a aproximação de diferenças finitas centrada :
onde e . Novamente obtemos um equação explicita no tempo que depende somente de e ;
Estabilidade
A abordagem que empregamos para demonstrar a estabilidade da equação da onda não homogênea é completamente análoga ao caso homogêneo. Em outras palavras, utilizamos o método de Von Neumann em conjunto com o teorema da estabilidade. Ao aplicar novamente as componentes de Fourier, representadas por , obtemos uma equação quadrática que impõe a seguinte restrição :
logo, o método é condicionalmente estável no intervalo .
Convergência, Consistência e Estabilidade
Até este ponto, ainda não discutimos o quão bem o esquema de diferenças finitas descreve a solução da equação diferencial. Vamos abordar isso agora. A propriedade mais essencial que um esquema deve possuir é que, à medida que os espaçamentos na malha discreta diminuem, a aproximação para a solução deve se aproximar da solução real do sistema. Portanto, um esquema é considerado uma boa aproximação se
onde é a solução exata e a solução aproximada. Se tais condições são satisfeitas, dizemos que o esquema de equações diferenciais finitas é convergente. Entretanto, geralmente, provar a convergência não é uma tarefa trivial. No entanto, podemos demonstrá-la de maneira indireta, utilizando estabilidade e consistência. Se um esquema é estável e consistente, então a convergência do esquema é garantida. Dada uma equação diferencial , dizemos que o esquema de diferenças finitas é consistente com a equação diferencial se, para qualquer função suficientemente diferenciável ,
Mostremos a consistência da aproximação de diferenças finitas para a equação da onda homogênea. Seja a EDP da onda
e seja a equação de diferenças finitas
pela aproximação que demonstramos anteriormente, temos :
como estamos supondo que os termos de ordem 2 são desprezíveis, e . Logo :
portanto o esquema de diferenças finitas é consistente. Como na seção anterior já havíamos provado a estabilidade condicional do método, podemos concluir que o esquema é condicionalmente convergente (é consistente e condicionalmente estável) e portanto representa uma boa aproximação para a solução exata da equação diferencial.
Análise espectral
Uma possível forma para quantitativamente analisar o som gerado por uma corda vibrante é estudar as frequências que compõem o seu movimento, técnica essa chamada de análise espectral. Antes de prosseguirmos vamos recapitular alguns resultados da álgebra linear
Supremacia da álgebra linear
O seguinte conjunto é o espaço de funções reais de uma variável. Esse conjunto é um espaço vetorial, logo podemos utilizar toda a artilharia da álgebra linear, em especial, estamos interessados no sub-espaço gerado pela base [4], pois elementos de , interpretados como sinais sonoros, representam um frequência pura de valor . Dessa forma, um sinal arbitrário pode ser escrito em termos das frequências puras que o formam
E podemos extrair suas coordenadas (conhecidas como transformada de Fourier do sinal) ( e ), fazendo o produto escalar com os elementos da base
Se o domínio de é limitado, digamos , então uma base infinita com cardinalidade enumerável (em contraste com a base anterior, que possui cardinalidade não enumerável) é suficiente para representar , uma possível base ortonormal é a seguinte: , em que . Dessa forma, a representação e coordenadas de ficam
É impossível falar sobre bases enumeráveis de um sub-espaço de sem representar esse canhão matemático com uma animação. Abaixo segue uma visualização que calcula as primeiras coordenadas ( e ) de um sinal qualquer e sobrepõem a série obtida, incrementando até as duas curvas serem indistinguíveis a olho nu.
Potência espectral
Adiante vamos ver que o sinal sonoro provém da vibração de um ponto específico da mesma, digamos em , então a função que representa o sinal é . Como estamos interessados nas frequências que compõem o sinal, será calculado a transformada de fourier de e definido que a potência da frequência é . A potência em função da frequência é o resultado da análise espectral.
Simulando uma corda de violão
Uma corda de violão geralmente é excitada por uma pancada dada por uma palheta ou pelo próprio dedo/unha do violonista. Essa pancada define uma condição inicial para a equação de onda. Uma suposição razoável da condição gerada é a seguinte
supondo que a corda possui comprimento e a pancado ocorreu em , causando uma deslocamento máximo . A imagem a seguir ilustra o estado da corda logo após a excitação
Dado essa condição inicial, podemos evoluir temporalmente o estado da corda utilizando a equação da onda, mantendo as bordas fixas (), mas como extrair som dessa simulação? Para responder essa pergunta precisamos saber como um violão gera som. Ao contrário do que inicialmente pareça, as ondas sonoras não são diretamente geradas pela vibração das cordas, mas sim da caixa do violão, que está diretamente conectada com as cordas em uma peça chamada ponte. A vibração das cordas gera uma força dependente do tempo que atua na caixa através da ponte, assim vibrando a caixa e gerando o som que escutamos. Portanto, para gerar som de forma realista, precisaríamos fisicamente simular a caixa, levando em consideração a sua geometria e as propriedades física do seu material, e então determinar as ondas de pressão que seriam geradas por essa vibração, o que está fora do escopo do presente trabalho. Felizmente, as seguintes simplificações vão nos permitir calcular as ondas de pressão:
- A força que a ponte exerce na caixa é aproximadamente proporcional a sua velocidade (Dinâmica aristotélica).
- A onda de pressão produzida pela caixa é aproximadamente proporcional a sua velocidade.
A força que a ponte exerce na caixa () é a força que a corda exerce na ponte (pois a ponte está firmemente conectada na caixa), e essa força é proporcional a inclinação da corda, ou seja
em que é a tensão na corda. Portando, o sinal da onda de pressão pode ser aproximado como o deslocamento de um ponto da corda próximo a ponte. Para gerar som com esse sinal, o tipo de arquivo WAV] é utilizado, pois o seu dado de entrada pode ser justante o sinal da onda de pressão.
Agora tudo está pronto para fazermos uma simulação, vamos tentar reproduzir a nota lá (). Primeiro precisamos descobrir qual deve ser a velocidade de propagação das ondas () para gerar a nota em questão. Resolvendo a equação da onda ideal, obtemos que as possíveis frequência que existem na solução são , então não é possível fazer a corda vibrar apenas com uma frequência, mas quando músicos se referem a uma nota, eles realmente estão se referindo a , a primeira frequência que compõem o sinal, portanto
Assumindo , temos que . Resolvendo a equação da onda realista pelo método FTCS com os seguinte parâmetros
| Parâmetros | Valor |
|---|---|
| h | 1 cm |
| Parâmetros | Valor |
|---|---|
| k | 1/4 |
| c | 880 m/s |
| 0,01 m | |
| L | 1 m |
| b | 5 |
obtemos o seguinte resultado
Na animação acima, por questão de comparação, também foi coloca a solução de uma simulação com os mesmos parâmetros, apenas com a modificação , que seria o caso ideal (sem amortecimento e rigidez).
Realizando a análise espectral do deslocamento de um ponto próximo de , obtemos o seguinte gráfico
As linhas verticais pretas e tracejadas representam as possíveis frequências da solução do caso ideal (também chamadas de harmônicos), ou seja, a primeira linha está em como era de se esperar, mas é notável que a segunda e quarta linhas possuem uma potência praticamente nula, isso ocorre porque a excitação inicial foi exatamente no meio, e as frequência correspondentes a essas linhas provém de ondas estacionário que possum um nodo em , logo elas não foram excitadas pela condição inicial. Mudando o ponto de excitação inicial, podemos ver essas frequências aparecendo. Rodando a simulação novamente, mas com , obtemos o seguinte espectro
Para observar a influência da rigidez, a simulação foi rodada com (10 vezes maior do que o valor anterior) resultando no seguinte espectro
O efeito mais notável é o deslocamento para esquerda das frequência em relação as frequências que compõem o sinal no caso ideal.
Por fim, conforme descrito anteriormente, podemos gerar som com as dados da simulação, mas infelizmente essa wiki não nos permite upar arquivos de áudio. No entanto, áudio das simulações discutidas aqui podem ser encontrados no repositório do projeto ana-julia dentro da pasta "sound". Em especial, o efeito de deslocamento de frequências causado pela rigidez é bastante evidente escutando os áudios.
Bônus
Apenas por diversão, segue uma animação de um pacote gaussiano como condição inicial
Notas
- ↑ Note que é periódica no tempo com período .
- ↑ As quantidades são chamadas de frequências naturais da corda; o fator é chamado modo natural de vibração e o período de modo natural de vibração é chamado de comprimento de onda.
- ↑ Perceba que não estamos operando expoentes, mas sim usando a relação entre os índices .
- ↑ A constante está presente por questão de normalização. Esse caso pode parecer um pouco estranho, dado que não é possível normalizar os cossenos e senos, pois sua integral em todo a reta não é definida, mas o que se deseja é a seguinte propriedade que é safisfeita quando .
Referências
- Giordano, Nicholas, Nakanishin Hisao. Computacional Physics, Sencond Edition - 2006.
- Strikwerda, John. Finite Diference Schemes and Partial Diferential Equations, Second Edition, SIAM - 2004.
- Moraes, Alciney das Neves. Critério de Estabilidade de um Esquema Explícito em Diferenças Finitas para o Modelo de Placas de Mindlin-Timoshenko, Universidade Federal do Pará — 2019.
- Grigoryan, Viktor. Finite differences for the wave equation. UC Santa Bárbara Mathematics - 2012.
- Boyce, E., W. Equações Diferenciais Elementares e Problemas de Valores de Contorno, 11ª Edição - 2020.








































































![{\displaystyle \left[0,X\right],\left[0,T\right]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9e25c0d437e20400267eeb9a7c6620f66be7e7c)










![{\displaystyle {\frac {\partial ^{2}y}{\partial t^{2}}}\approx {\frac {\partial }{\partial t}}\left({\frac {y_{j}^{n+1}-y_{j}^{n}}{\Delta t}}\right)\approx {\frac {1}{\Delta t}}\left[{\frac {y\left(t+\Delta t,x\right)-y\left(\left(t+\Delta t\right)-\Delta t,x\right)}{\Delta t}}-{\frac {y\left(t,x\right)-y\left(t-\Delta t,x\right)}{\Delta t}}\right]={\frac {y\left(t+\Delta t,x\right)+y\left(t-\Delta t,x\right)-2y\left(t,x\right)}{(\Delta t)^{2}}}={\frac {y_{j}^{n+1}+y_{j}^{n-1}-2y_{j}^{n}}{(\Delta t)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b01bd4e7e6ea0ac9a9aa6c7f3e1143ca1955a024)








![{\displaystyle \xi \in \left[-\pi /\Delta x,\pi /\Delta x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16287749202a8bc3727f87713665348318c321a2)






![{\displaystyle B^{n+1}+B^{n-1}=B^{n}\left[2\left(1-a^{2}\right)+a^{2}\left(e^{ik\Delta x}+e^{-ik\Delta x}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9c1466ca7780e75544782192173526ead535fe4)




![{\displaystyle A+{\frac {1}{A}}=-2\left[2a^{2}sen^{2}\left({\frac {k\Delta x}{2}}\right)-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f703b90c01efc935b1517e6028dddcdc8fdda4)
















![{\displaystyle a\in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8d53d4d97039bd1a0a95c7908e5514a8efb2018)

![{\displaystyle {\frac {\partial ^{2}y}{\partial t^{2}}}=c^{2}\left({\frac {\partial ^{2}y}{\partial x^{2}}}-\epsilon L^{2}{\frac {\partial ^{4}y}{\partial x^{4}}}\right)-2b{\frac {\partial y}{\partial t}}\mapsto y_{j}^{n+1}=\left[\left(2-2a^{2}-6\epsilon a^{2}E^{2}-F\right)y_{j}^{n}-y_{j}^{n-1}+a^{2}\left(1+4\epsilon E^{2}\right)\left(y_{j+1}^{n}+y_{j-1}^{n}\right)-\epsilon a^{2}E^{2}\left(y_{j+2}^{n}+y_{j-2}^{n}\right)\right]\left({\frac {1}{1-F}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d212091c105fda7e67000daf23958f0e33456a7)



![{\displaystyle a\in \left[0,1/4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b220bb53faa272ebbd0de85abb9e242f609c8fa1)

















![{\displaystyle s(t)={\frac {1}{\sqrt {\pi }}}\int _{0}^{\infty }[a(\omega )cos(\omega t)+b(\omega )sen(\omega t]d\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f60836a43ecad380efef72d017bc0fcc88e3e08)



![{\displaystyle t\in [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7ea7b28971838e52f450c48053939e81daa26f)


![{\displaystyle {\begin{aligned}s(t)&=a_{0}{\sqrt {\frac {1}{T}}}+{\sqrt {\frac {2}{T}}}\sum _{n=1}^{\infty }{\bigg [}a_{n}cos(\omega _{n}t)+b_{n}sen(\omega _{n}){\bigg ]}\\a_{0}&=\int _{0}^{T}s(t){\sqrt {\frac {1}{T}}}dt\\a_{n}&=\int _{0}^{T}s(t){\sqrt {\frac {2}{T}}}cos(\omega _{n}t)dt\\b_{n}&=\int _{0}^{T}s(t){\sqrt {\frac {2}{T}}}sen(\omega _{n}t)dt\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2fd87ac955714b2926998725fad6f42b07cffb)