Belousov-Zhabotinsky: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 125: | Linha 125: | ||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
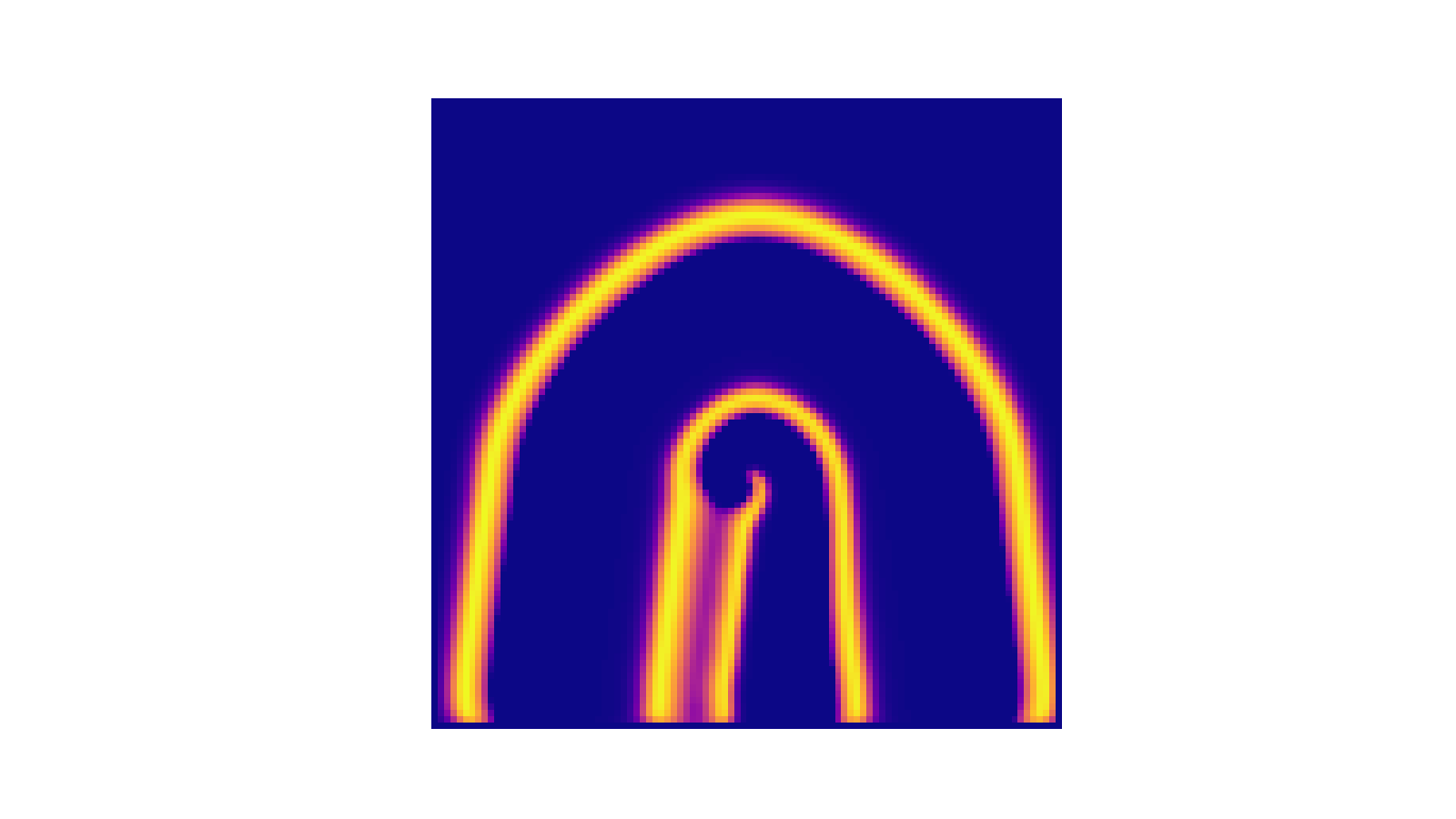
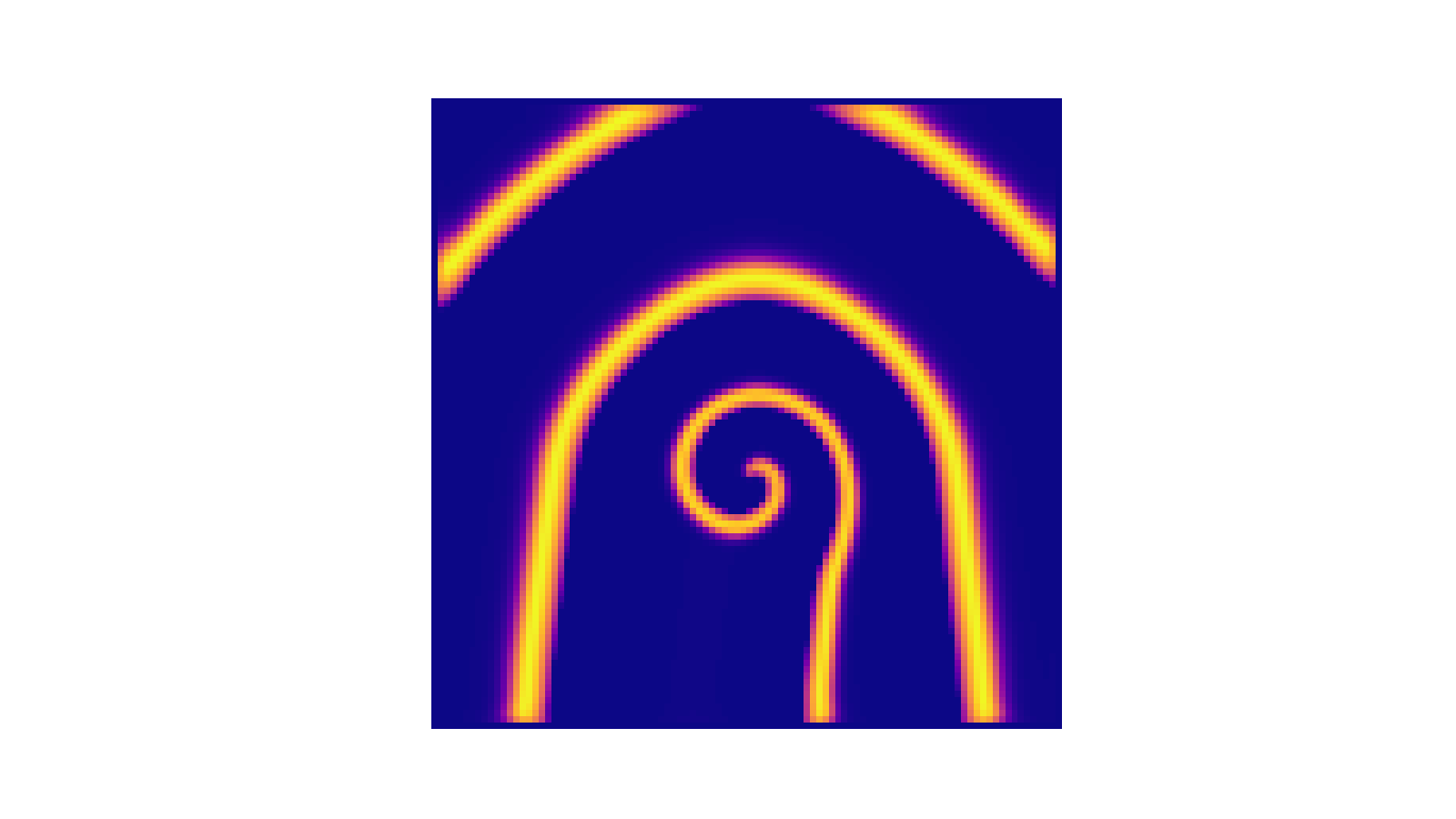
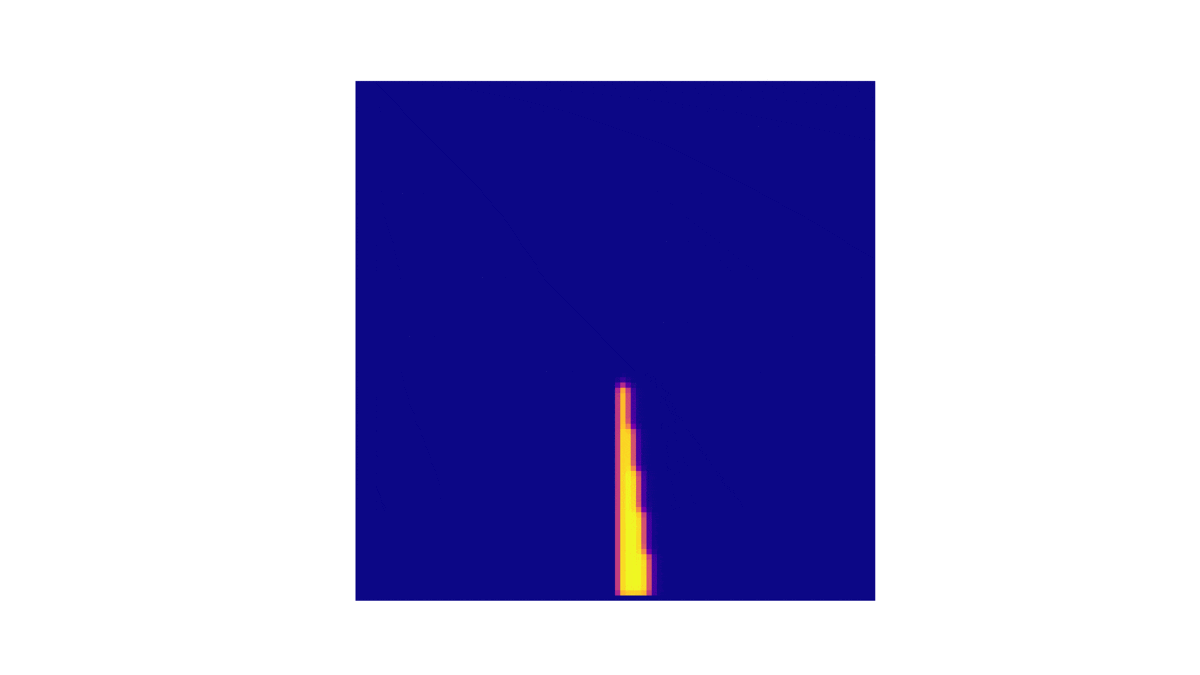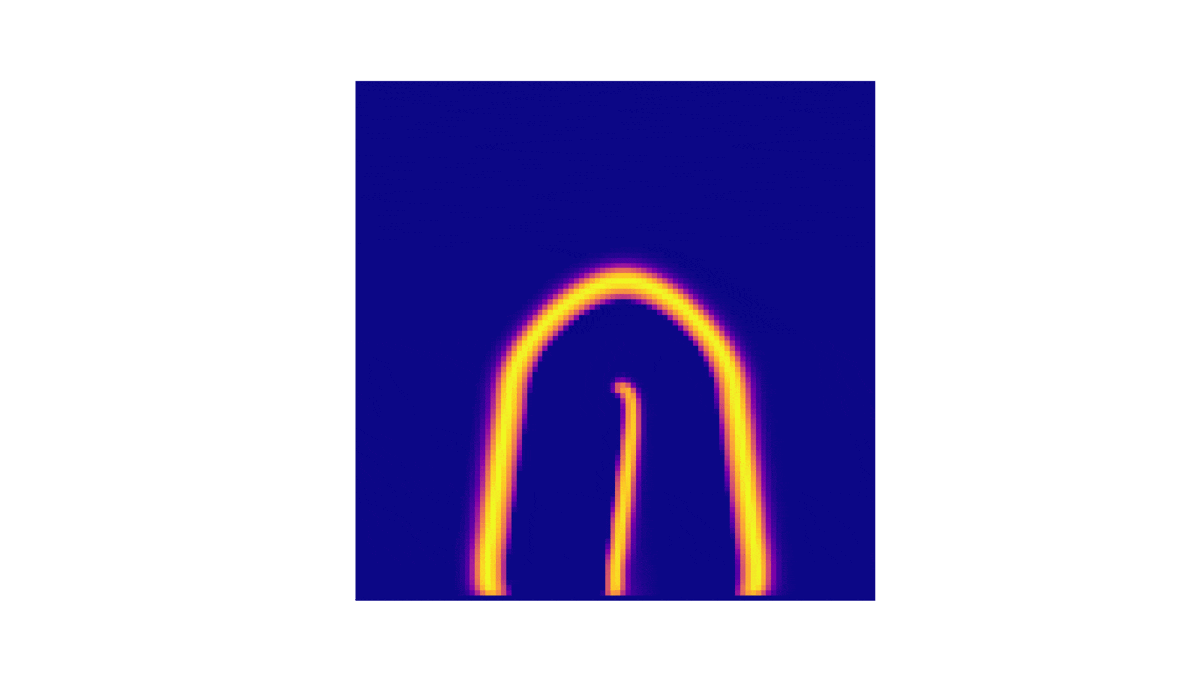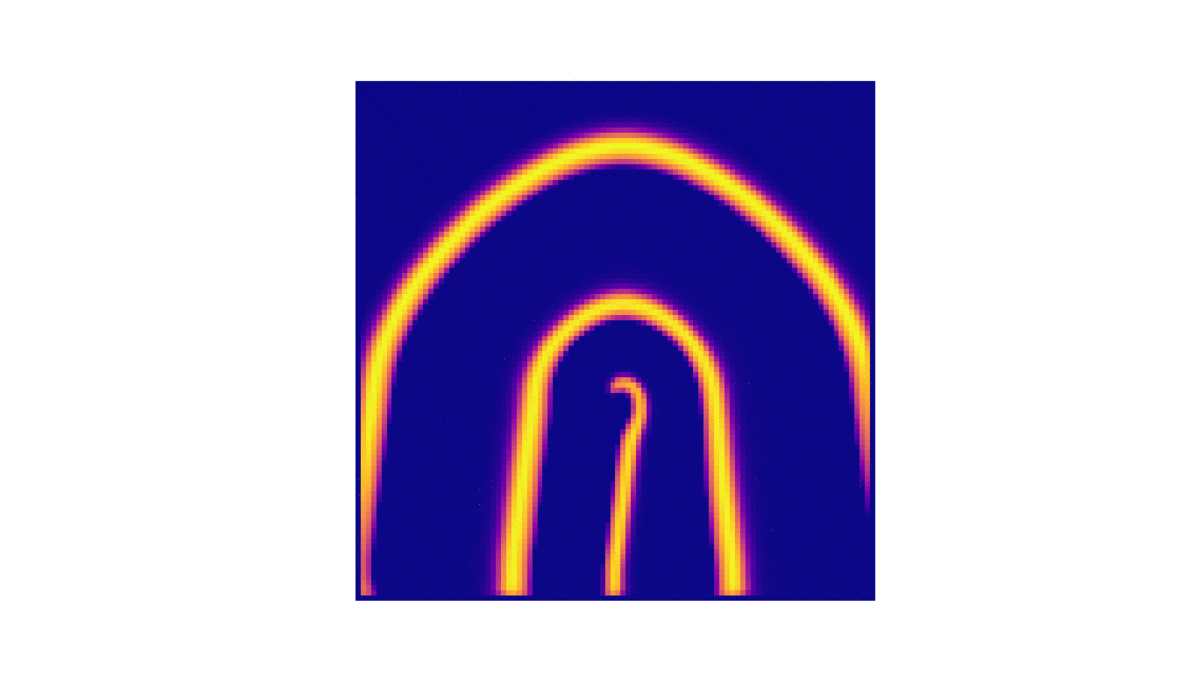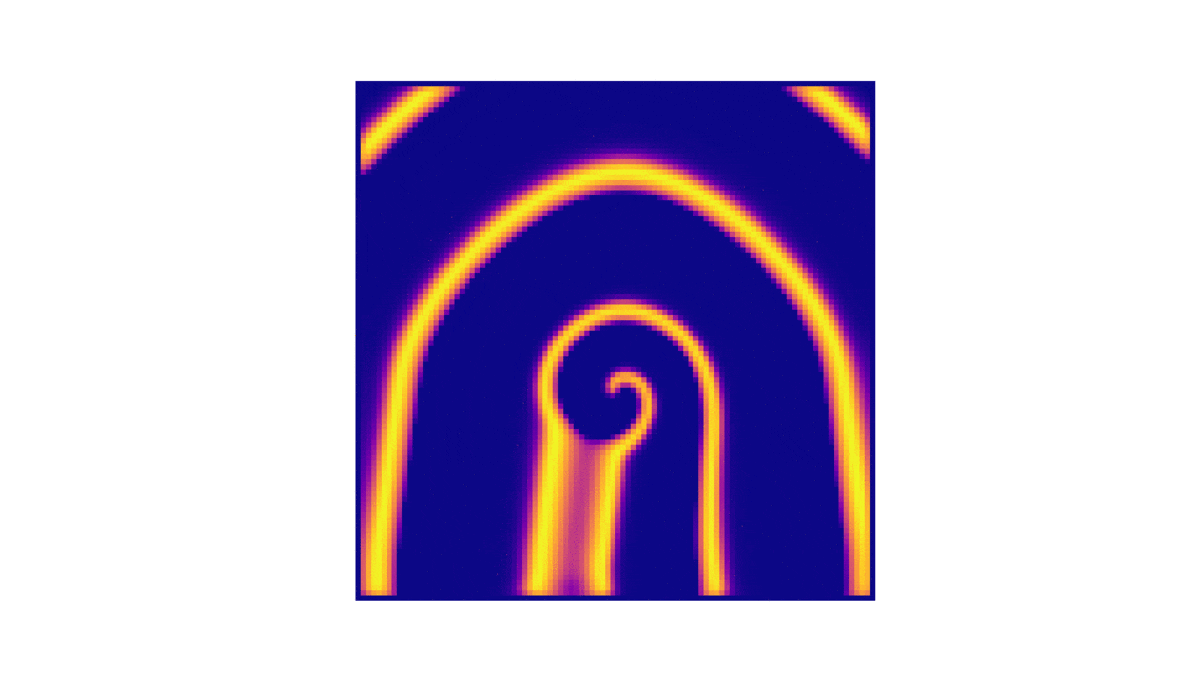
!colspan=" | !colspan="3"|Analise da concentração de u com <math>(e, q, f) = (0.2, 10^{-3}, 1)</math> <math>(D_u, D_v) = (10^{-5}, 10^{-5} )</math> | ||
|- | |||
|[[Arquivo:U00000.png|thumb|upright=4|none|alt=Alt text|t = 0.|300px]] | |||
|[[Arquivo:U12000.png|thumb|upright=4|none|alt=Alt text|t = 12000.|300px]] | |||
|[[Arquivo:U25000.png|thumb|upright=4|none|alt=Alt text|t = 25000.|300px]] | |||
|- | |||
|[[Arquivo:U38000.png|thumb|upright=4|none|alt=Alt text|t = 38000.|300px]] | |||
|[[Arquivo:U50000.png|thumb|upright=4|none|alt=Alt text|t = 50000.|300px]] | |||
|[[Arquivo:U63000.png|thumb|upright=4|none|alt=Alt text|t = 63000.|300px]] | |||
|- | |- | ||
|[[Arquivo: | |[[Arquivo:U75000.png|thumb|upright=4|none|alt=Alt text|t = 75000.|300px]] | ||
|[[Arquivo: | |[[Arquivo:U88000.png|thumb|upright=4|none|alt=Alt text|t = 88000.|300px]] | ||
|[[Arquivo:U100000.png|thumb|upright=4|none|alt=Alt text|t = 100000.|300px]] | |||
|- | |- | ||
|} | |} | ||
| Linha 137: | Linha 145: | ||
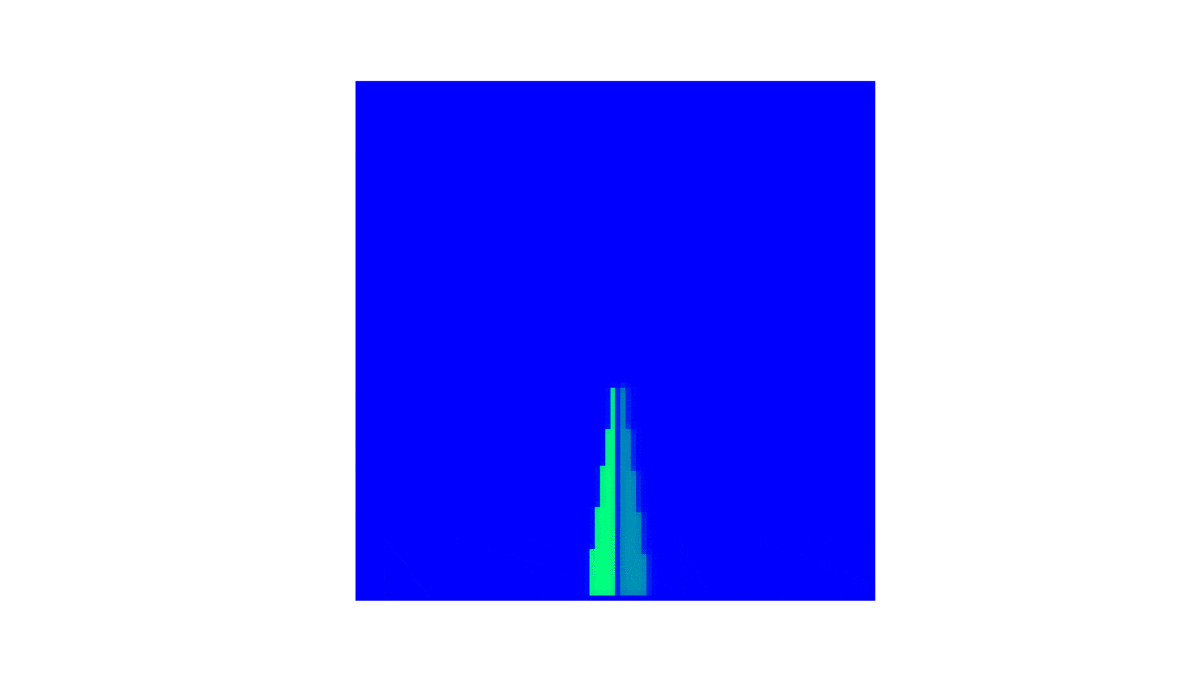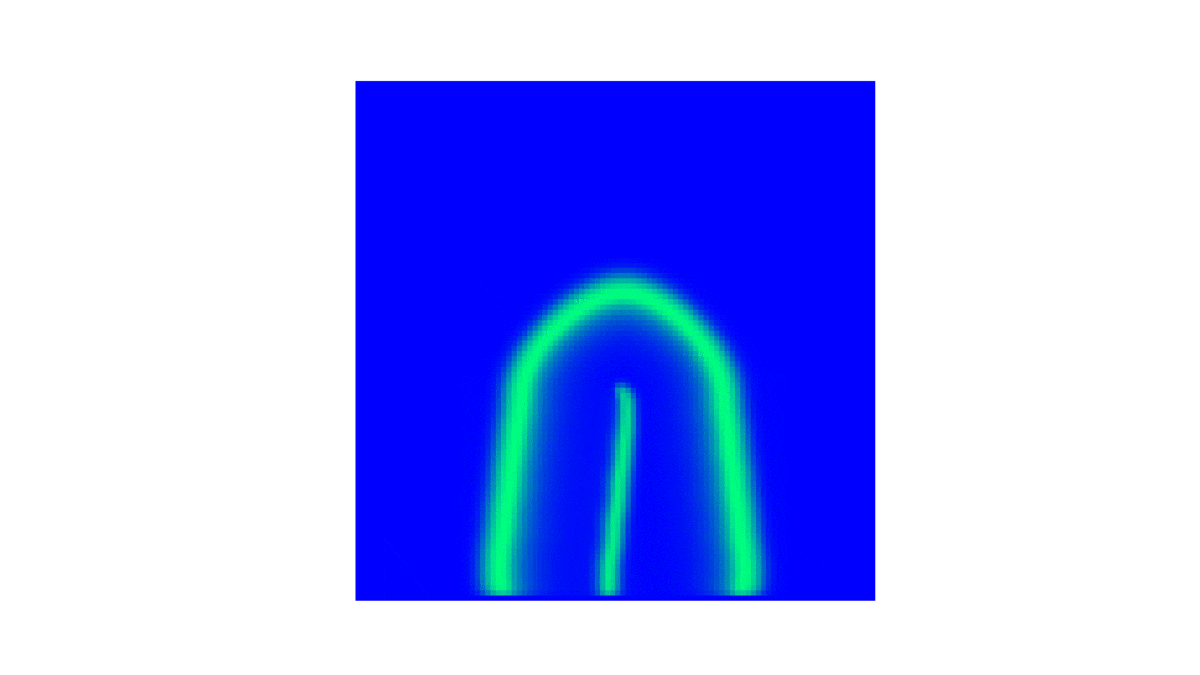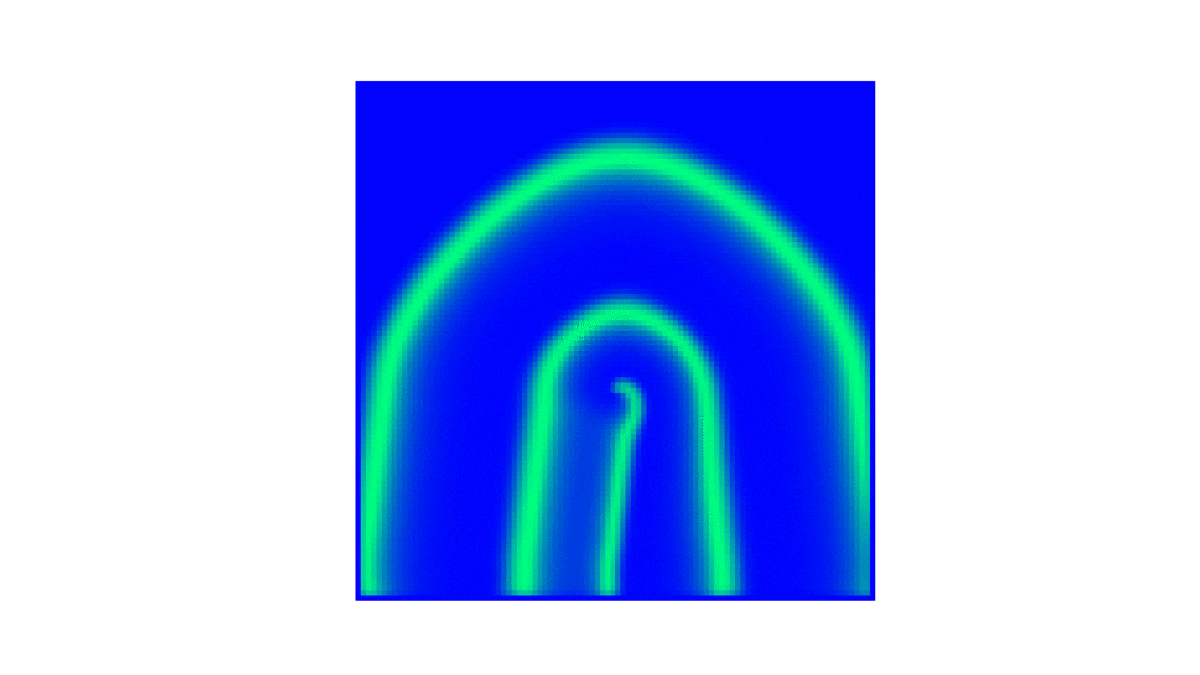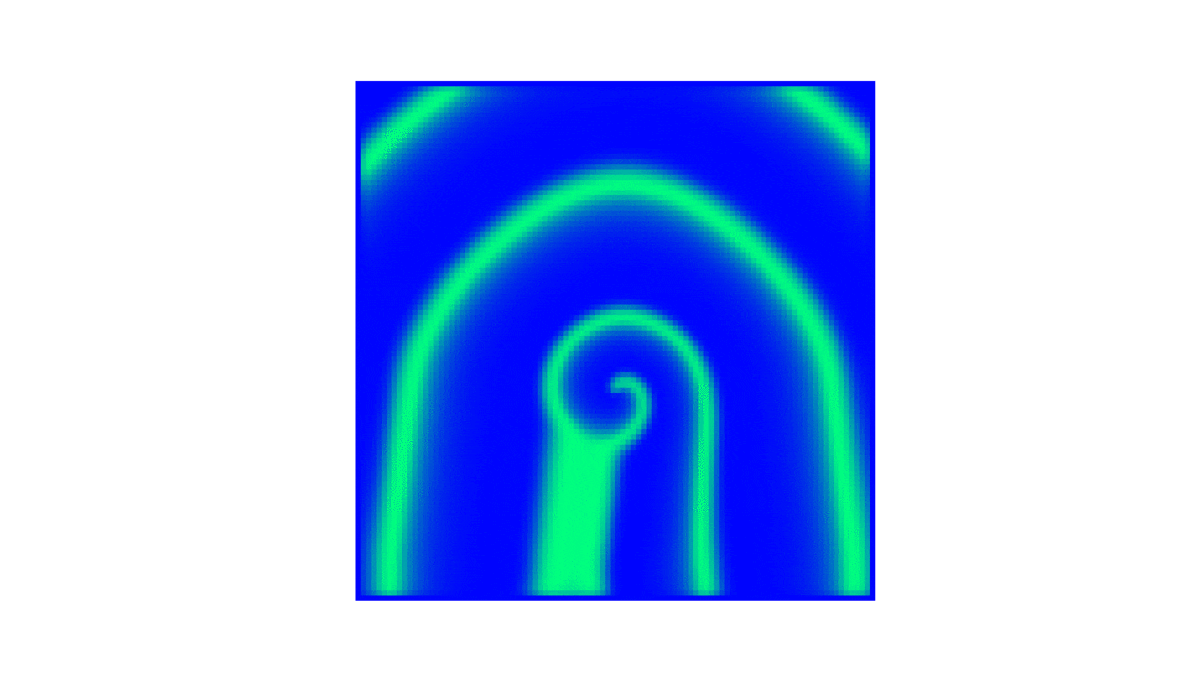
!colspan="2"|BZ com <math>(e, q, f) = (0.2, 10^{-3}, 1)</math> <math>(D_u, D_v) = (10^{-5}, 10^{-5} )</math> | !colspan="2"|BZ com <math>(e, q, f) = (0.2, 10^{-3}, 1)</math> <math>(D_u, D_v) = (10^{-5}, 10^{-5} )</math> | ||
|- | |- | ||
|[[Arquivo: | |[[Arquivo:U20k.gif|thumb|upright=4|none|alt=Alt text|BZ da concentração de <math> u </math> até t = 20k.|500px]] | ||
|[[Arquivo: | |[[Arquivo:V20k.gif|thumb|upright=4|none|alt=Alt text|BZ da concentração de <math> v </math> até t = 20k.|500px]] | ||
|- | |- | ||
|} | |} | ||
== Programas Utilizados == | == Programas Utilizados == | ||
Edição das 06h35min de 7 de abril de 2021
Belousov-Zhabotinsky Reaction
A reação de Belousov-Zhabotinsky[1] [2] (BZ) consiste em uma família de reações químicas oscilatórias descobertas inicialmente por Belousov, e posteriormente analisadas por Zhabotinsky. A reação consiste em 3BrO3− + 5CH2(CO2H)2 + 3H+ → 3BrCH(CO2H)2 + 4CO2 + 5H2O + 2CH2O2, e demonstra um comportamento oscilatório não linear até atingir o equilíbrio químico. A interação entre a reação e a difusão dos produtos químicos no espaço resultará na auto-organização de ondas viajantes dinâmicas. Seu mecanismo original, foi descrito através de 27 espécies químicas e um total de 80 reações.
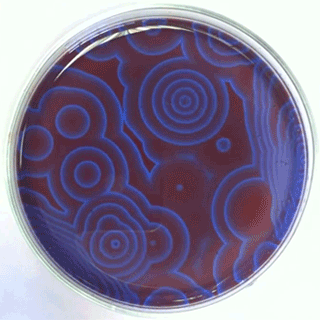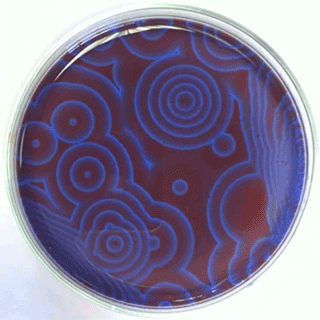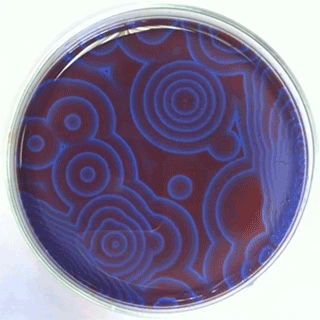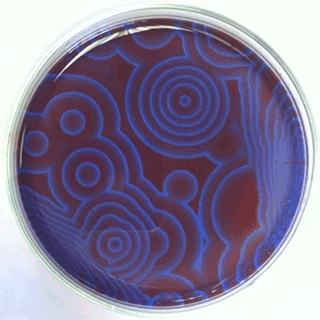
Oregonator
Oregonator[2] é um modelo matemático utilizado para descrever de forma mais simples a dinâmica da reação BZ, desenvolvido por Field e Noyes (1974). Foi um modelo não espacial originalmente composto por três variáveis de estado, onde posteriormente, vemos que tornam-se apenas duas. O mecanismo é, inicialmente composto por cinco etapas irreversíveis, onde, A = 3BrO3 -, B = 5CH2(COOH)2; 2HCOOH, 3BrCH(COOH)2 (no geral, estas e demais espécies orgânicas); P = HOBr; X = HBrO2; Y = Br-; Z = forma oxidada do catalisador e f é o coeficiente estequiométrico. Observamos também. suas respectivas equações de taxa, onde v é a taxa da reação e ki corresponde às constantes de taxa de reação:
| A + Y | X + P | v1 = k1 [A][Y] | |||||||||||||||||
| X + Y | 2 P | v2 = k2 [X][Y] | |||||||||||||||||
| A + X | 2 X + 2 Z | v3 = k3 [A][X] | |||||||||||||||||
| 2 X | A + P | v4 = k4 [X]2 | |||||||||||||||||
| B + Z | Y | v5 = k5 [B][Z] |
Para construir o modelo Oregonator, é necessário supor que as concentrações de A e B permaneçam constantes (estão associadas às concentrações iniciais dos precursores). Posteriormente, deve-se aplicar as técnicas padrão de cinética química para obter o modelo dinâmico considerando X, Y e Z como variáveis dinâmicas, assumindo que as reações químicas são elementares, ou seja, os coeficientes estequiométricos coincidem com a potência das variáveis dinâmicas. Considerando como o tempo, vemos as seguintes equações de velocidade:
A análise é simplificada convertendo essas equações em uma forma adimensional:
A partir de operações algébricas com as equações acima, obtemos para x, y e z, o seguinte sistema de equações diferenciais não lineares:
Onde , e , e seus respectivos valores típicos são , e . Como o parâmetro (que é obtido através de reações experimentais), é possível ver que y muda na escala do tempo de forma muito mais rápida que as demais variaveis, e então, assumimos que é sempre determinado pelos valores instantâneos de e , e assim, reescrevemos y como :. Deste modo, as equações são reduzidas para [4]:
Dessa forma, o modelo de Oregonator mostra a forma típica de um sistema de feedback químico, ou seja, a variável x, que será reescrito como u, funciona como um ativador, enquanto a variável z, que será reescrita como v, tem o papel de inibidor. Se para as equações termos associados à difusão são adicionados, onde Du e Dv são os coeficientes de difusão adimensionais, e é o operador Laplaciano, então, o sistema torna-se:
Implementação
Antes de discretizarmos a equação para que assim possamos utiliza-la em um código, explicaremos brevemente métodos e fórmulas utilizados para isso.
Método FTCS (Forward Time Centered Space)[5]
De modo a resolver numericamente as equações descritas acima, serão utilizado o método FTCS (Forward Time Centered Space), que consiste em um método para resolver equações parciais através da derivada parcial de primeira ordem no tempo por uma diferença finita e progressiva e a derivada parcial de segunda ordem no espaço por uma diferença centrada, como vemos logo abaixo:
Laplaciano
O Laplaciano pode tanto ser representado por quanto por . O laplaciano é a soma de todas as derivadas parciais simples de segunda ordem:
Seja
Como o código para Belousov-Zhabotinsky terá apenas 2 dimensões o ficará da seguinte forma:
De modo a simplificar a expressão para analises posteriores, reescreveremos desta forma, considerando uma analise 2D:
Aplicação dos Métodos para a Reação de Belousov-Zhabotinsky
Considerando a equação :
Considerando a equação :
Resultados
| Analise da concentração de u com | ||
|---|---|---|
| BZ com | |
|---|---|
Programas Utilizados
Simulaçao Belousov-Zhabotinsky
Referências
- ↑ H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems", p. 287. Open SUNY Textbooks, Geneseo, NY, 2015.
- ↑ 2,0 2,1 Harzola-Flores J.A., García E., Rojas J.F, Spatial and temporal dynamics of Belousov-Zhabotinsky reaction: A STEM approach (2020), Revista Mexicana de Física E 17 (2) 178–190
- ↑ https://gfycat.com/uk/discover/belousov-zhabotinsky-reaction-gifs
- ↑ http://www.scholarpedia.org/article/Oregonator#Eq-4
- ↑ https://pt.wikipedia.org/wiki/Esquema_FTCS



![{\displaystyle {\frac {d[X]}{d\tau }}=k_{1}[A][Y]-k_{2}[X][Y]+k_{3}[A][X]-2k_{4}[X]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/715ad1dc6644bec6887cfb9486b0a78a0c3f36d9)
![{\displaystyle {\frac {d[Y]}{d\tau }}=-k_{1}[A][Y]-k_{2}[X][Y]+{\frac {1}{2}}fk_{5}[B][Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6138ff9935ac9b1aeab507db9e2ade36e01abb0b)
![{\displaystyle {\frac {d[Z]}{d\tau }}=2k_{3}[A][X]-k_{5}[B][Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2d731319245feffcf2c6f71b80c6b27519e296)
![{\displaystyle x\equiv {\tfrac {2k_{4}[X]}{k_{3}[Y]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93410756cc47976115c80ed65f9bfaf2edd32b7)
![{\displaystyle y\equiv {\tfrac {k_{2}[X]}{k_{3}[A]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa8e37c6fa0bdff1688e23d441788e8ad4acef81)
![{\displaystyle z\equiv {\tfrac {k_{5}k_{4}[B][Z]}{(k_{3}[A])^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7194e6a6618c3e72d1df0838dc23dc62501bbfc7)
![{\displaystyle t\equiv k_{5}[B]\tau }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a56551b07de9cc7ef3f2056b910212ca6a04afa1)

![{\displaystyle \epsilon \equiv {\tfrac {k_{5}[B]}{k-{3}[A]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128a92c4917b485c046a5c3ba8e6c6d4ce73e8a2)
![{\displaystyle \epsilon '\equiv {\tfrac {2k_{4}k_{5}[B]}{k_{2}k_{3}[A]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abe50ed1d313cdb91a5a9f49323b979a7ecc8790)
























![{\displaystyle u_{C}^{n+1}-u_{C}^{n}=\left[u_{C}(1-u_{C})+f{\frac {q-u_{C}}{q+u_{C}}}v_{C}+D_{u}\left({\frac {u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{\Delta h^{2}}}\right)\right]{\frac {\Delta t}{\epsilon }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed505d785de13af6549ce0c84f8aa0b33dadaf12)
![{\displaystyle u_{C}^{n+1}=u_{C}+\left[u_{C}(1-u_{C})+f{\frac {q-u_{C}}{q+u_{C}}}v_{C}+D_{u}\left({\frac {u_{R}+u_{L}+u_{U}+u_{D}-4u_{C}}{\Delta h^{2}}}\right)\right]{\frac {\Delta t}{\epsilon }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd147f5892b55414cf9797342a0f68605f6b742)


![{\displaystyle v_{C}^{n+1}-v_{C}^{n}=\left[u_{C}-v_{C}+D_{v}\left({\frac {v_{R}+v_{L}+v_{U}+v_{D}-4v_{C}}{\Delta h^{2}}}\right)\right]\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a897f09378abc1226ceed5afd0d244b6b3e260)
![{\displaystyle v_{C}^{n+1}=v_{C}+\left[u_{C}-v_{C}+D_{v}\left({\frac {v_{R}+v_{L}+v_{U}+v_{D}-4v_{C}}{\Delta h^{2}}}\right)\right]\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f2542134e54f4250f84845e584a092ea0bf8e3)