Analisar a estabilidade local de equações diferenciais atrasadas é mais desafiador que realizar a mesma análise para equações diferenciais ordinárias. Isto ocorre devido a dimensionalidade infinita do sistema. Por exemplo considerando uma equação diferencial linear atrasada simples:

Onde  , só há um único ponto de equilíbrio em
, só há um único ponto de equilíbrio em  . Para equações diferenciais ordinárias do tipo:
. Para equações diferenciais ordinárias do tipo:

Assumindo que as soluções vão ser da forma  , pode-se substituir:
, pode-se substituir:

Então este é o polinômio característico. E sua solução nos dá a solução para a equação diferencial. Por exemplo:

Logo  . Esta solução pode ser conferida resolvendo diretamente esta EDO simples:
. Esta solução pode ser conferida resolvendo diretamente esta EDO simples:

Agora supondo uma solução análoga  para a equação com atraso:
para a equação com atraso:

E

Então a equação característica é:

Para as equações diferenciais ordinárias havia um polinômio e o teorema fundamental da álgebra permitia dizer quantas raízes esperar. Porém para as equações diferenciais atrasadas, não há teorema algum sobre a quantidade de raízes, este número poderia inclusive ser infinito. Como exemplo, pode-se considerar soluções reais e complexas separadamente conforme será visto na sequência.
Solução real
Supondo que a solução é real, pode-se plotar  e
e  separadamente, e então e procurar por intersecções. Isto é, quando os dois termos possuem o mesmo valor para um mesmo
separadamente, e então e procurar por intersecções. Isto é, quando os dois termos possuem o mesmo valor para um mesmo  , pois consequentemente então
, pois consequentemente então  . Se
. Se  , há uma única intersecção, onde
, há uma única intersecção, onde  , então
, então  aumenta exponencialmente ao infinito quando
aumenta exponencialmente ao infinito quando  . Desta forma, o ponto de equilíbrio é instável.
. Desta forma, o ponto de equilíbrio é instável.

A esquerda o gráfico gerado para um valor qualquer em que

, e a direita para três valores em que

, especificamente

em preto,

em verde, e

em azul.
Se  pode haver 2 intersecções
pode haver 2 intersecções  , 1 intersecção o
, 1 intersecção o  ou nenhuma intersecção
ou nenhuma intersecção  . Para identificar qual é este ponto crítico
. Para identificar qual é este ponto crítico  , basta perceber que neste ponto a reta
, basta perceber que neste ponto a reta  é tangente à curva
é tangente à curva  no ponto
no ponto  . Logo, a inclinação de ambos deve ser a mesma,
. Logo, a inclinação de ambos deve ser a mesma,  . A inclinação da reta
. A inclinação da reta  é simplesmente
é simplesmente  . Então a inclinação da curva também deve ser:
. Então a inclinação da curva também deve ser:


Substituindo a constante  em
em  :
:

Pode-se obter agora  a partir da reta
a partir da reta  ,
,  . Dessa forma o valor crítico é então
. Dessa forma o valor crítico é então  . Logo, se
. Logo, se ![{\textstyle \alpha \in \left[\alpha _{c}0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a97c2975f38f9c294de6b1e02194046ae3d88b9f) , então as raízes da equação característica são reais e negativas e a solução exponencial associada decai para
, então as raízes da equação característica são reais e negativas e a solução exponencial associada decai para  com o tempo. As raízes
com o tempo. As raízes  também são chamadas de autovalores, termo que será empregado daqui em diante.
também são chamadas de autovalores, termo que será empregado daqui em diante.
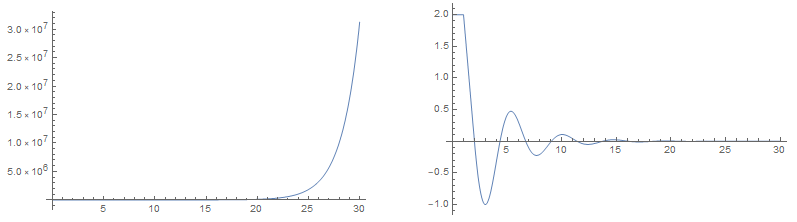
A esquerda a solução para

e a direita para

, considerando como condição inicial

.
Para  , não há decaimento ou crescimento exponencial nos componentes da solução, para isto vamos analisar as soluções complexas. As soluções podem ser obtidas numericamente via Mathematica:
, não há decaimento ou crescimento exponencial nos componentes da solução, para isto vamos analisar as soluções complexas. As soluções podem ser obtidas numericamente via Mathematica:
sol = NDSolve[{y'[t] == -2.0*y[t - 1], y[t /; t <= 1] == 2}, y, {t, 0, 30];
Plot[y[t] /. sol, {t, 0, 30}, PlotRange -> All]
Solução Complexa
Substituindo então  , na equação característica, obtém-se:
, na equação característica, obtém-se:
![{\displaystyle {\begin{aligned}\lambda -\alpha e^{-\lambda }&=0\\\lambda &=\alpha e^{-\lambda }\\\lambda _{r}+i\lambda _{i}&=\alpha e^{\left[-\lambda _{r}-i\lambda _{i}\right]}\\\lambda _{r}+i\lambda _{i}&=\alpha e^{-\lambda _{r}}e^{-i\lambda _{i}}\\\left[\lambda _{r}\right]+i\left[\lambda _{i}\right]&=\left[\alpha e^{-\lambda _{r}}\cos \lambda _{i}\right]+i\left[\alpha e^{-\lambda _{r}}\sin \left(-\lambda _{i}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7ffcca924e66120d05ebe342d4edc480a8f5da0)
Logo:

Calculando a razão entre os termos:

Então utilizando  como parâmetro, pode-se obter equações paramétricas para
como parâmetro, pode-se obter equações paramétricas para  e
e  :
:

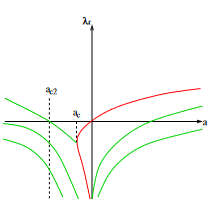
Soluções das equações paramétricas. Em vermelho o caso especial quando

.
Por conta da periodicidade das funções trigonométricas, muitas curva são traçadas quando varía-se  entre
entre  e
e  . Além, disto para
. Além, disto para  então
então  , desta forma pode-se plotar diretamente
, desta forma pode-se plotar diretamente  :
:

Ele ocorre quando  e
e  e
e  . Então substituindo:
. Então substituindo:

Logo

E substituindo:

Usando a propriedade  então:
então:

Então:

Então estes são os valores de

em que temos

. Novamente pode ser visualizado via Geogebra:
((-1)^n (-n π - π / 2),0)
((-1)^n (+n π - π / 2),0)
Para  , obtém-se então o ponto crítico desejado:
, obtém-se então o ponto crítico desejado:

O primeiro ponto no eixo negativo de  em que tem-se
em que tem-se  . Logo, o ponto de equilíbrio é estável se
. Logo, o ponto de equilíbrio é estável se  , se não, é instável. Pode-se observador que os resultados obtidos para o caso em que os autovalores eram apenas reais está contido neste resultado.
, se não, é instável. Pode-se observador que os resultados obtidos para o caso em que os autovalores eram apenas reais está contido neste resultado.
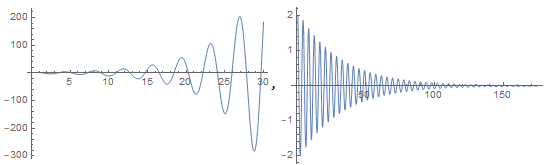
A esquerda a solução para

e a direita para

, considerando como condição inicial

.
Antes de concluir, pode-se prestar uma atenção especial para o ponto em que as soluções complexas encontram a solução real, este é exatamente o primeiro ponto crítico. Lembrando que o primeiro ponto crítico era  , este resultado concorda com a equação obtida para
, este resultado concorda com a equação obtida para  :
:

E também no limite das equações paramétricas:

No Mathematica:
{Limit[-Cot[x]*x, x -> 0], Limit[-x/(Exp[x*Cot[x]]*Sin[x]), x -> 0]}
Principais materiais utilizados
- Delay-Differential Equations (Richard Bertram, Universidade Estadual da Flórida)
- Homogeneous Differential Equations (Paul Dawkins, Universidade de Lamar)










































![{\textstyle \alpha \in \left[\alpha _{c}0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a97c2975f38f9c294de6b1e02194046ae3d88b9f)







![{\displaystyle {\begin{aligned}\lambda -\alpha e^{-\lambda }&=0\\\lambda &=\alpha e^{-\lambda }\\\lambda _{r}+i\lambda _{i}&=\alpha e^{\left[-\lambda _{r}-i\lambda _{i}\right]}\\\lambda _{r}+i\lambda _{i}&=\alpha e^{-\lambda _{r}}e^{-i\lambda _{i}}\\\left[\lambda _{r}\right]+i\left[\lambda _{i}\right]&=\left[\alpha e^{-\lambda _{r}}\cos \lambda _{i}\right]+i\left[\alpha e^{-\lambda _{r}}\sin \left(-\lambda _{i}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7ffcca924e66120d05ebe342d4edc480a8f5da0)





































