Lennard-Jones e propriedades termodinâmicas

Nesta página apresentamos uma simulação de Dinâmica Molecular utilizando o potencial de Lennard-Jones como potencial de interação entre as partículas.

Potencial de Lennard Jones

O potencial de Lennard Jones representa a interação entre os àtomos ou moléculas. Possui dois termos distintos: um repulsivo devido às forças de troca do princípio de exclusão de Pauli (origem quântica) e um atrativo devido às forças de van der Walls.

$V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right].$

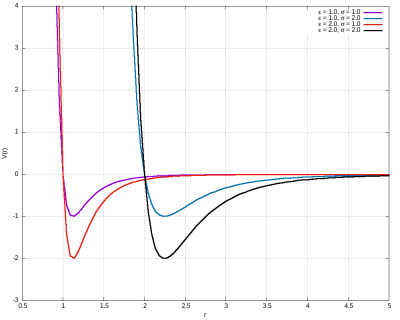
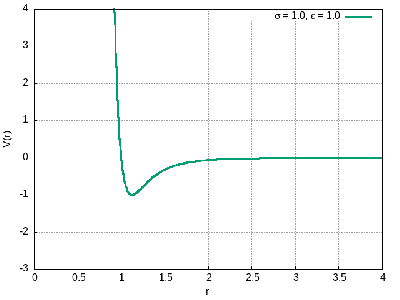
O termo proporcional à ${\frac {1}{r^{6}}}$ é o termo atrativo, enquanto o termo proporcional à ${\frac {1}{r^{12}}}$ é o termo repulsivo, muito mais intenso à curtas distâncias. A constante $\epsilon$ descreve a profundidade do poço deste potencial, enquanto $\sigma$ descreve a posição do ponto de equilíbrio estável. Nas imagens abaixo, podemos ver o comportamento do potencial para diferentes valores de $\epsilon$ e $\sigma$.

Potencial de Lennard-Jones.

Comportamento do potencial de Lennard-Jones para diferentes valores de $\epsilon$ e $\sigma$.

A força que uma partícula sofre, quando sujeita a este potencial é dada por

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{F}(\boldsymbol{r}) &=& -\nabla V(\boldsymbol{r})} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{F}(\boldsymbol{r}) &=& 4\epsilon\left[12\frac{\sigma^{12}}{r^{13}} - 6\frac{\sigma^6}{r^7}\right]}

Dinâmica Molecular

A abordagem da dinâmica molecular se baseia em integrar as equações de movimento newtonianas para todas as partículas do sistema. Abaixo, podemos sintetizar um resumo dos passos para realizar uma simulação de dinâmica molecular.

1. Inicializar a posição e velocidade das partículas do sistema.

2. Calcular as forças de interação entre todas as partículas do sistema.

3. Integrar as equações de movimento utilizando algum algoritmo integrador.

4. Medir grandezas físicas, como energia cinética, energia potencial, temperatura e pressão.

Existem algumas características que devem ser levadas em consideração quando fazemos uma simulação de dinâmica molecular. Como integrar as equações de movimento requer um poder computacional elevado para muitas partículas, fazemos uma simulação de um "pedaço" do sistema de interesse. Construímos este "pedaço" como uma caixa de lado L e confinamos nossas partículas neste espaço. O número de partículas permanecesse constante e quando uma partícula atravessa a fronteira da caixa, ela retorna do outro lado. Isso simula um sistema infinito. Esta condição de contorno é chamada de condição de contorno periódica (Periodic Boundary Condition - PBC).

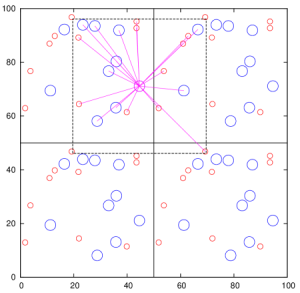
Outra característica importante é a convenção da imagem mínima. Esta característica diz respeito à interação entre as partículas. Como cada partícula interage com todas as outras, se a distância entre as partículas for maior do que a metade da caixa, ou seja, L/2, então devemos imaginar que ela vai interagir com a partícula correspondente na caixa "ao lado". Isso é uma extensão do conceito de sistema infinito discutido anteriormente. Ao lado temos uma figura que esquematiza este conceito.

Convenção da imagem mínima.

Simulação

Nesta simulação, utilizamos um sistema

Bibliografia

D. Frenkel, B. Smit. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press. 2002.