Movimento Browniano Geométrico para Previsão no Mercado de Ações
Grupo: Eric Naiber, Vitória Xavier
Forecasting é uma palavra da língua inglesa que dá ideia de fazer uma previsão que pode não ser certeira, esta é a palavra que define bem o que realizamos ao longo deste trabalho. A ideia é fazer um forecasting do preço das ações de determinada empresa (utilizamos neste trabalho os dados do Magazine Luiza/MGLU3) utilizando de métodos matemáticos e futuramente estatísticos junto de algoritmos escritos na linguagem Python.
Mercado de ações
O mercado de ações de uma forma mais generalizada é quando temos um conjunto de empresas colocando à venda uma porcentagem/fração de seu capital social, esta fração é conhecida como uma ação. O valor de uma ação é volátil, podendo variar muito tanto para cima quanto para baixo em um curto intervalo de tempo, podendo trazer grandes lucros ou grandes prejuízos, como por exemplo: Em 2021 o preço unitário de uma ação do Magazine Luiza custava em média 20 reais, e hoje (09/05/2022) o preço não passa dos 5 reais. Uma queda tão drástica quanto esta traz aos investidores inúmeras inseguranças e incertezas quanto ao futuro, se seria viável investir novamente ou não. Para o entendimento do que foi feito neste trabalho, o que foi dito é o suficiente, porém quanto mais conhecimento sobre mundo financeiro, melhor o aproveitamento. Recomendamos o livro “Os Axiomas de Zurique” para o leitor interessado em entender mais sobre o assunto.
Movimento Browniano e Movimento Browniano Geométrico
Em 1828, o biólogo Robert Brown observou comportamento irregular e ininterrupto de grãos de pólen suspensos em água, o que posteriormente foi nomeado de Movimento Browniano [1]. Acreditava-se que esse movimento aleatório era advindo de uma força vital do próprio pólen. Quase 80 anos se passaram com diferentes pesquisadores tentando desvendar a natureza do movimento browniano até que Einstein, em 1905, obteve a expressão matemática que caracterizou esse comportamento. O movimento do pólen sobre a água não tratava-se de um fenômeno biológico, mas sim físico. Mostrou que esse movimento se dá pelo choque com outras partículas, gerando movimento não contínuo[2]. Sua solução representou grandes avanços para física e química, e dentre elas lançou as bases de uma das teorias mais bem sucedidas para a modelagem de sistemas naturais.
Einstein, em 1905 [3], com relação ao primeiro experimento em que o movimento browniano foi observado, demonstrou que o número de partículas suspensas em um ponto do espaço com relação a um instante temporal assumia uma distribuição gaussiana. Além disso, o MB é um processo markoviano, dado que seu estado futuro depende apenas do presente, e não de eventos passados [4][5]. Portanto, o movimento Browniano é tido como um modelo referencial para processos estocásticos e usado para entender diferentes sistemas em não equilíbrio. Esse modelo pode ser aplicado no estudo de comportamento de diversos sistemas dotados de movimentos aleatórios cuja distribuição de probabilidades seja gaussiana. A fórmula do movimento browniano é dada por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\left(t\right)=\sigma W\left(t\right)}
Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
é a variância e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{t}}
o processo de Wiener. Sua distribuição normal é dada por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\:~\:\left[0,\:s-t\right]}
Movimento Browniano Geométrico
O movimento browniano geométrico é a distribuição logarítmica do movimento browniano, gerando apenas valores positivos e provocando um deslocamento na curva gaussiana pelo qual o MB é caracterizado. Ele é definido pela equação diferencial estocástica abaixo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dS_{t}=\mu S_{t} dt+\sigma S{t} dW{t}, t\:\in \left[t_0,\:T\right]}
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(t)}
é processo estocástico, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{t}}
um processo de Wiener, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu }
é a deriva ou deslocamento e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
é a volatilidade, ambas são constantes.
Para resolvermos a equação, apresentaremos rapidamente o lema de Itô, identidade para encontrar o diferencial de funções de processos estocásticos dependentes de tempo. É dado por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dy\left(t,\:X_t\right)=\frac{\partial y}{\partial t}\left(dt\right)+\frac{\partial \:y}{\partial \:X_t}\left(dX_t\right)+\frac{1}{2}\frac{\partial ^{\:2}y}{\partial \:X^2_t}\left(dX^2_t\right)}
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
é a função do processo estocástico dependente do tempo e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{t}}
é o processo estocástico. Vamos renomear o processo estocástico para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{t}}
. Agora, iremos aplicar transformação logarítmica, ferramenta que será relevante nos próximos passos.
$$ g\left(S_t\right)=ln\left(S_t\right) $$
Aplicando o lema de Itô no nosso sistema:
$$ dg\left(t,\:S_t\right)=\frac{\partial g}{\partial t}\left(dt\right)+\frac{\partial \:g}{\partial \:S_t}\left(dS_t\right)+\frac{1}{2}\frac{\partial ^{\:2}g}{\partial \:S^2_t}\left(dS^2_t\right) $$
Aplicando $g(S_t) = ln(S_t)$, temos que as derivadas parciais são:
$$ \frac{\partial g}{\partial t}\left(dt\right)=0, \frac{\partial g}{\partial S_t}\left(dS_t\right)=\frac{1}{S_t}, \frac{\partial ^2g}{\partial S^2_t}\left(dS^2_t\right)=-\frac{1}{S^2_t} $$
E utilizando propriedades de cálculo estocástico:
$$ dS^2_t=\sigma ^2S^2_tdt $$
A substituição e desenvolvimento desses valores e a equação $dS_t$ na equação $dg(t, S_t)$ resulta em:
$$ dg\left(S_t\right)=\left(\mu -\frac{1}{2}\sigma ²\right)dt+\sigma \:dW_t $$
Integrando ambos lados da equação, chegamos em:
$$ g\left(S_t\right)-g\left(S_{t_0}\right)=\left(\mu -\frac{1}{2}\sigma ^2\right)\left(T-t_0\right)+\sigma \left(W_t-W_{t_0}\right) $$
Aplicando o logaritmo em ambos lados da equação, como sugerido anteriormente, temos:
$$ ln\left(\frac{S_t}{S_{t_0}}\right)=\left(\mu -\frac{1}{2}\sigma ^2\right)\left(T-t_0\right)+\sigma \left(W_t-W_{t_0}\right) $$
$$ exp\left(ln\left(\frac{S_t}{S_{t_0}}\right)\right)=exp\left(\left(\mu -\frac{1}{2}\sigma ^2\right)\left(T-t_0\right)+\sigma \left(W_t-W_{t_0}\right)\right) $$
E finalmente chegamos na solução da equação diferencial estocástica do movimento browniano geométrico:
$$ S_t=S_{0\:}exp\left(\left(\mu -\frac{1}{2}\sigma ^2\right)\left(T-t_0\right)+\sigma \left(W_t-W_{t_0}\right)\right) $$
Ou
$$ S_t=S_{0\:}exp\left(\left(\mu -\frac{1}{2}\sigma ^2\right)t+\sigma W_t\right) $$
Sua distribuição normal é dada por:
$$ N\:~\:\left[\left(\mu -\frac{\sigma ^2}{2}\right)t,\:\sigma ^2t\right] $$
Sendo o primeiro termo a média e o segundo a variância.
Graficamente, a diferença entre movimento browniano e movimento browniano geométrico é apresentado abaixo[6]:
Aplicação: Mercado Financeiro
Mercado financeiro é a plataforma de compra e venda de ativos financeiros, sendo eles ações, títulos, mercadorias e linhas de crédito. Seus agentes são o investidor, que tem o papel de emprestar dinheiro com a expectativa de receber lucro sobre ele, e o tomador de dinheiro, pessoa física ou jurídica que toma o dinheiro e o devolve ao investidor com juros mais tarde. O mercado de capitais é o setor do mercado financeiro que negocia as operações de venda e compra de ações. O investidor, ao comprar a ação, pode participar da sociedade da empresa ou receber parte do lucro dela. O objetivo do investidor é ganhar dinheiro com a valorização das ações e de sua venda.
No Brasil, essa plataforma de negociação é a bolsa de valores IBOVESPA, localizada em São Paulo. Em 2021, mais de 400 companhias brasileiras estavam listadas na B3 (como também chama-se a IBOVESPA) [7].
O valor de uma ação flutua dependendo de diferentes fatores, como economia, geopolítica, etc. Por isso, toda compra e venda de ações possui um risco intrínseco de perda de dinheiro devido à dificuldade de estimar o valor futuro. O investidor deve constantemente estar buscando informações para auxiliar no seu processo de decisão sobre compra, venda ou manutenção dos capitais. Os principais parâmetros para entender a movimentação do mercado de capitais são o preço das ações, a volatilidade financeira e o retorno de investimento:
- Preço da ação: é o valor máximo recebido ao para vender uma ação ou o valor mínimo pago para comprar a ação. [8].
- Volatilidade financeira: vulnerabilidade que o preço da ação tem a eventos, causando grandes oscilações do seu valor. É um parâmetro importante para garantir segurança na tomada de decisão.
- Retorno sobre investimento: é o de lucro ou perda que o investidor teve sobre o valor investido.
O comportamento do mercado financeiro é estudado a partir de diferentes abordagens, com objetivo de elaborar estratégias para previsão dos índices ou preços futuros das ações, buscando maximizar o lucro do investidor.
A teoria do passeio aleatório é utilizada no campo das finanças, onde descreve que os processos no mercado de ações evoluem como um passeio aleatório e que predição não é possível [9]. O próximo movimento será determinado a partir do estado atual e não de estados passados, configurando um processo markoviano [10].
Assumindo que o mercado de ações possui comportamento estocástico e similar ao passeio aleatório, é possível utilizar modelos matemáticos que, a partir de dados que descrevem o cenário de compra e venda atual, descrevem possíveis cenários futuros de preço de ações e auxiliam o investidor a tomar decisões menos arriscadas.
Como citado na seção acima, o movimento Browniano é um tipo de caminhada aleatória. O movimento browniano geométrico, variação do movimento browniano padrão, assume apenas valores positivos e é amplamente utilizado no mercado financeiro. Aplicado ao mercado de ações, é definido pela equação:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(t)=S(0)exp((\mu-(\sigma ^2)/2)t+\sigma W_{t})}
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(t)} é o valor futuro da ação, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(o)} é o valor inicial da ação, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} é o deslocamento (“drift”) diário, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} é a volatilidade diária e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_{t}} é o processo de Wiener. O termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} é um parâmetro de taxa de crescimento, onde seu valor positivo sinaliza tendência de crescimento e negativo sinaliza tendência de queda.
O MBG é um modelo muito utilizado no mercado financeiro por assumir propriedade markoviana, gerar apenas valores reais e ser de fácil implementação. Suas desvantagens é que o parâmetro volatilização é constante e não ocorrem os “jumps”, eventos maiores que afetam o cenário de maneira mais drástica (o caminho não é descontínuo) [11]
O MBG é assumido no modelo de Black-Scholes, modelo avançado e bastante utilizado nas simulações de economia. A ideia central deste modelo é enxergar o mercado como um sistema dinâmico de muitos corpos, tornando possível traçar analogias com conceitos da termodinâmica[12].
Esse trabalho irá trabalhar com o MBG apenas.
Simulações
A ideia é gerar números pseudo-aleatórios com um comportamento provável do preço da ação, os resultados serão discutidos mais adiante.
Para fazer as simulações foram necessárias 6 etapas.
Etapa 1: Adquirir os dados
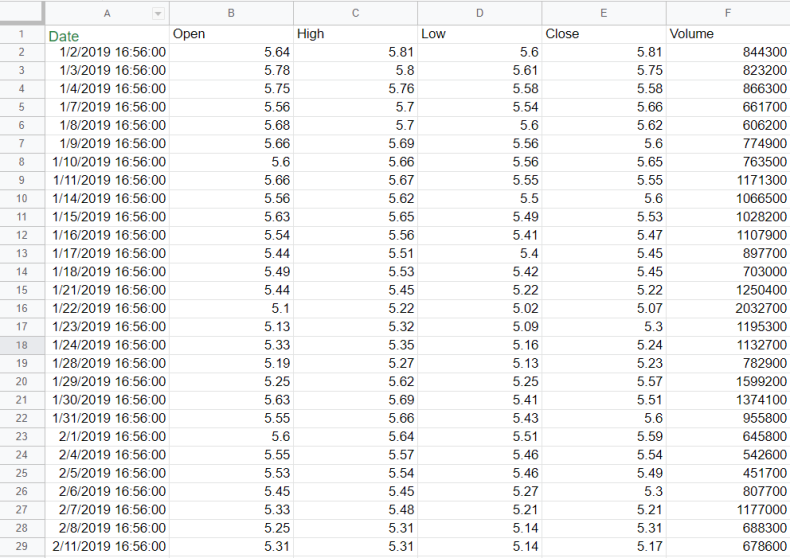
Utilizamos o Google Sheets para baixar um documento .csv que continha todos os dados necessários, na figura abaixo é possível ver como os dados estão distribuídos na planilha.
Temos na tabela os valores máximos, mínimos, de abertura e fechamento de preço das ações, junto de sua data e volume (que não nos interessa).
Etapa 2: Cálculos iniciais necessários
Precisamos da Taxa de Retorno Diária, Volatilidade Diária e Desvio Médio para poder gerar um número pseudo-aleatório que tenha um comportamento similar ao do preço da ação. Antes, é interessante fazer um paralelo entre mercado financeiro e o MBG.
| Mundo Financeiro | Movimento Browniano Geométrico |
|---|---|
| Taxa de Retorno Diária | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} |
| Volatilidade Diária | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} |
| Desvio Médio | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Drift} |
Para calcular a Taxa de Retorno Diária fazemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu =\sum _{i=1}^n\left(\frac{xi}{n}\right)}
onde a soma de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle xi} é a taxa de retorno anual, já Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} é a quantidade de dias que o mercado ficou aberto para trocas. Esta taxa dita o tamanho médio do passo em que a simulação percorrerá.
Agora para calcular a Volatilidade Diária:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma =\frac{\sum _{i=1}^n\left(xi-\mu \right)^2}{n}}
onde o somatório da diferença da Taxa de Retorno Diária menos uma parte da taxa de retorno anual é chamada de Volatilidade Anual. A volatilidade mostra o tamanho base extra que a simulação irá percorrer.
Por último temos o Drift, que mostra o tamanho e direção do passo dado na simulação (considerando uma distribuição normal):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Drift=\mu -\frac{1}{2}\sigma ^2}
Etapa 3: Aplicar à simulação
Utilizando o MBG, a tabela com as informações das ações e os valores calculados acima, é possível calcular o preço futuro da ação com base no que já ocorreu da seguinte forma:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\left(t\right)=S\left(0\right)e^{\left(Drift\right)t+\sigma Z}}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\left(t\right)}
é o preço futuro da ação, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\left(0\right)}
é o preço atual da ação e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z}
é um número aleatório de 0 até 1 que segue uma distribuição normal.
Discussão e Resultados
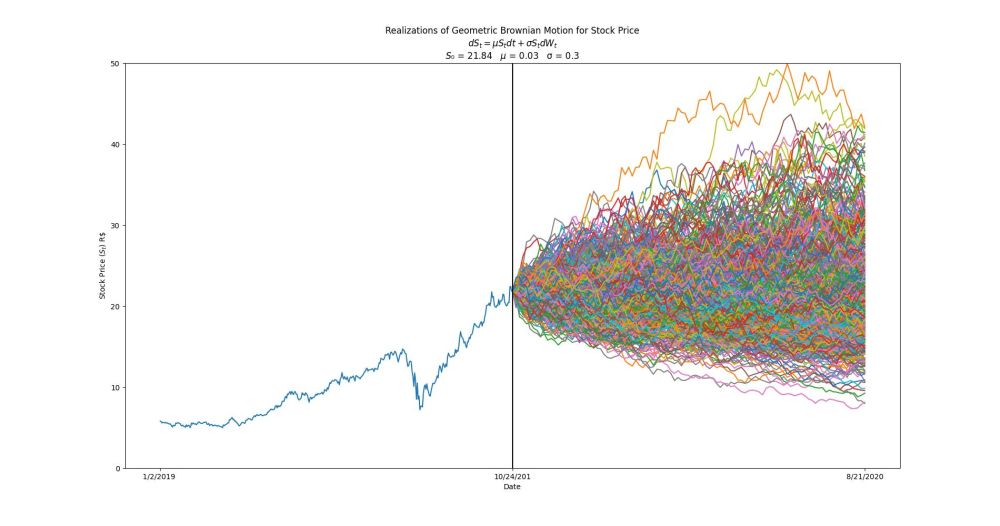
Para a empresa em análise (Magazine Luiza) foi observado primeiramente o comportamento real do preço de fechamento da ação, como possível de se observar no gráfico abaixo. No eixo vertical temos o preço e no horizontal o tempo, a linha preta no meio demonstra o período em que a simulação irá começar a acontecer (intervalo entre 1 ano real e 1 ano simulado).
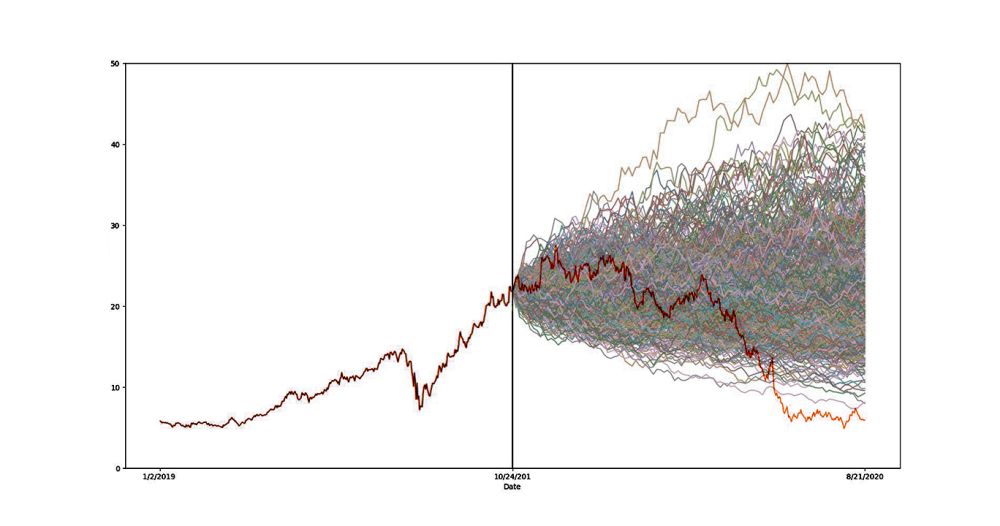
Logo após a linha preta foi dado início às simulações, cada linha mostra um possível comportamento da ação, o usuário poderia (vendo o gráfico) tomar algum tipo de decisão e/ou criar um planejamento estratégico financeiro para os cenários onde o preço da ação é máximo após 1 ano (linha vertical preta) ou onde o valor é mínimo.
Por fim uma análise é feita comparando ambos os gráficos, é possível perceber que o caminho real que o preço da ação percorre está dentro do esperado para um cenário negativo, onde o preço da ação está em queda. A ideia seria que o usuário estivesse se planejado financeiramente para que o prejuízo não seja tão alto.
Funciona?
A pergunta que fica é: realmente funciona para prever o preço de uma ação?
A resposta é não. O mercado financeiro é muito mais complexo e possui um comportamento quase aleatório (se observado microeconomicamente), não é possível prever o preço de uma ação se baseando apenas no que ocorreu no passado, se fosse assim, a empresa que estudamos teria uma curva de crescimento indefinida, algo que não ocorre. Podemos sim fazer métodos matemáticos e estatísticos para analisar possíveis cenários, mas da forma em que fizemos esta ainda muito arcaico, porém serve bem para demonstração da ideia.
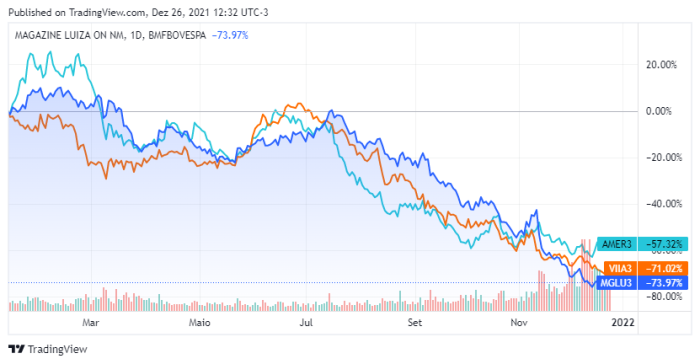
Como melhorar a simulação?
Podemos começar colocando pesos na geração de números aleatórios, onde cada ação (como mostrado na figura *, de empresas de varejo) influencia a outra, ou seja, se a maioria das empresas de varejo estão em queda isso deverá pesar, fazendo com que o próximo valor tenha uma probabilidade maior de cair também. Mas mesmo fazendo tudo o que foi comentado, teríamos apenas valores possíveis para o preço de uma ação, e nunca o valor certo. Concluindo, utilizar MBG (junto do método de Monte Carlo se possível) não será satisfatório para prever o preço de uma ação, mas sim para poder ver caminhos possíveis que a ação poderá tomar, fazendo com que o usuário consiga fazer um planejamento estratégico financeiro para evitar prejuízos e maximizar possíveis lucros.
Código para Simulação
Para gerar os gráficos acesse o link [[2]].
Código utilizado para as simulações.
import numpy as np
import matplotlib.pyplot as plt
"""
Previsão do valor de mercado MAGLU3
Data inicial: 02/01/2019
Data final: 19/04/2022
"""
Untreated = []
# Data original
OriginalDate = []
# Colocando o Valor do final do dia.
OriginalStockPrice = []
"""
Coluna | Significado
0 | Data
1 | Hora
2 | Open
3 | High
4 | Low
5 | Close
6 | Volume
"""
with open('STOCK.csv', 'r', encoding='utf8') as f:
for line in f:
Untreated.append(line.split(','))
Untreated.pop(0)
for i in Untreated:
"""
Open = float(i[1])
High = float(i[2])
Low = float(i[3])
"""
Close = float(i[4])
OriginalDate.append(i[0][0:9])
OriginalStockPrice.append(Close)
# Data para monte carlo
Date = OriginalDate[0:int(len(OriginalDate) / 2)]
# Stock final do dia monte carlo
StockPrice = OriginalStockPrice[0:int(len(OriginalDate) / 2)]
mean = np.nanmean(StockPrice)
std = np.nanstd(StockPrice)
var = np.nanstd(StockPrice) ** 2
#######################
# Stochastic Differential Equation (SDE):
# dS(t) = mu S(t) dt + sigma S(t) dW(t)
# Explicit Expression:
# S(t) = S0 exp( (mu - sigma^2/2) t + sigma W(t) )
######## Cte's ########
# drift coefficent
mu = mean - 0.5 * var
# number of steps
n = 100
# time in years
T = 1
# number of sims
M = 500
# initial stock price
S0 = StockPrice[-1]
# volatility
sigma = 0.3
######## Simulating GBM Paths ########
# calc each time step
dt = T / n
# simulation using numpy arrays
St = np.exp(
(mu - sigma ** 2 / 2) * dt
+ sigma * np.random.normal(0, np.sqrt(dt), size=(M, n)).T
)
# include array of 1's
St = np.vstack([np.ones(M), St])
# multiply through by S0 and return the cumulative product of elements along a given simulation path (axis=0).
St = S0 * St.cumprod(axis=0)
######## Consider time intervals in years. ########
# Define time interval correctly
time = np.linspace(0, T, n + 1)
# Require numpy array that is the same shape as St
tt = np.full(shape=(M, n + 1), fill_value=time).T
######## Plotting. ########
def OriginalPlot(graph=False):
plt.figure(figsize=(19, 10))
Date_in_slice = np.linspace(0, 2, num=len(OriginalDate))
plt.plot(Date_in_slice, OriginalStockPrice)
plt.title(f'MGLU3 - 2 Years.\nStart: {OriginalDate[0]}\nEnd: {OriginalDate[-1]}')
plt.xticks([0, 1, 2], [Date[0], Date[int(len(Date) / 2)], Date[-1]])
plt.xlabel('Date')
plt.ylabel('Stock Price R$')
plt.vlines(1, 0, 60, colors='black')
plt.ylim(0, 50)
plt.savefig("1OriginalPlot.jpeg")
if graph:
plt.show()
def FinalPlot(graph=False):
plt.figure(figsize=(19, 10))
Date_in_slice = np.linspace(-1, 0, num=int(len(OriginalDate) / 2))
plt.plot(Date_in_slice, StockPrice)
plt.plot(tt, St)
plt.xlabel("Date")
plt.ylabel("Stock Price $(S_t)$ R\$")
plt.xticks([-1, 0, 1], [Date[0], Date[int(len(Date) / 2)], Date[-1]])
# "Realizations of Geometric Brownian Motion for Stock Price $dS_t = \mu S_t dt + \sigma S_t dW_t$\n $S_0 = R${0}, \mu = {1}, \sigma = {2}$"
# $ for itallic, \sigma, \mu
plt.title(f"Realizations of Geometric Brownian Motion for Stock Price\n"
f"$dS_t = \mu S_t dt + \sigma S_t dW_t$\n"
f"$S\u2080$ = {StockPrice[-1]:.2f} $\u03BC$ = {mu:.2f} \u03C3 = {sigma}")
plt.ylim(0, 50)
plt.vlines(0, 0, 60, colors='black')
plt.savefig('2SimulationPlot.jpeg')
if graph:
plt.show()
OriginalPlot()
FinalPlot()
Referências
- ↑ R. Brown, Phil. Mag. 4, 161 (1828).
- ↑ A. Einstein, Ann. d. Phys. 17, 549 (1905).
- ↑ A. Einstein, Ann. d. Phys. 17, 549 (1905).
- ↑ Wilmott, P., 2000. Quantitative Finance. John Wiley & Son, Ltd, Chichester
- ↑ A Review on Geometric Brownian Motion in Forecasting the Share Prices in Bursa Malaysi
- ↑ Caesar Wu, Rajkumar Buyya. Chapter 18 - Real Option Theory and Monte Carlo Simulation. Cloud Data Centers and Cost Modeling. 2015. Pages 707-772. [ISBN 9780128014134](https://fiscomp.if.ufrgs.br/index.php/Especial:Fontes_de_livros/9780128014134) . [1](https://doi.org/10.1016/B978-0-12-801413-4.00018-0)
- ↑ https://blog.toroinvestimentos.com.br/empresas-listadas-b3-bovespa#:~:text=A%20B3%2C%20conhecida%20anteriormente%20como,mais%20de%20100%20empresas%20estrangeiras. Acesso em: 30 de abril de 2022.
- ↑ NurAimiBadriah, N, SitiNazifah, Z. A. and Maheran, M. J., Forecasting Share Prices Accurately For One Month Using Geometric Brownian Motion, 26 (4): 1619 - 1635 (2018).
- ↑ Kobeissi Y. H, Multifractal Finance Markets: An Alternative Approach to Asset and Risk Management, springer, New York. (2012).
- ↑ Farida Agustini W, IkaRestuAffianti, Endah RM Putri, Stock price prediction using geometric Brownian motion, International Conference on Mathematics: Pure, IOP -974 012047(2018).
- ↑ Caesar Wu, Rajkumar Buyya. Chapter 18 - Real Option Theory and Monte Carlo Simulation. Cloud Data Centers and Cost Modeling. 2015. Pages 707-772. ISBN 9780128014134. https://doi.org/10.1016/B978-0-12-801413-4.00018-0.
- ↑ Black and Scholes, 1973; Merton, 1973.