Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou

Grupo: Paula Pandolfo, Ramiro de Souza, Samuel Dieterich e Wallace Carvalho

Objetivo: Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas as análises de resultados serão restritas aos casos unidimensionais, por simplicidade. Inicialmente será introduzido o formalismo de oscilações acopladas lineares. [falta complementar]

Introdução

Os osciladores são talvez os sistemas mais estudados na Física, sendo capazes de modelar uma ampla gama de fenômenos, como, p. ex., pêndulos, circuitos eletrônicos, interações moleculares. O comportamento linear desses sistemas, em particular, possui resultados analíticos bem conhecidos.

O problema de FPUT (Enrico Fermi, John R. Pasta, Stanislaw M. Ulam, Mary Tsingou) resulta da análise computacional de um sistema de partículas que apenas interagem com seus vizinhos, com interações modeladas por oscilações acopladas com a adição de um termo não-linear, que pode ser quadrático ou cúbico. O intuito original da simulação era estudar como esse sistema evolui para o equilíbrio térmico. Se as forças fossem estritamente lineares, a energia alocada em cada modo de vibração não se distribuiria entre os demais modos, ou seja, não se atingiria o equilíbrio térmico. Entretanto, com a adição dos termos não lineares, pelo Teorema da Equipartição da Energia, supunha-se que, após um certo tempo, a energia total do sistema seria distribuída uniformemente entre os modos normais de vibração, o que significaria que o sistema teria atingido o equilíbrio térmico. Entretanto, isso não foi observado.

O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo que relatou o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).

A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores lineares acoplados. A seguir, compararemos esses resultados com simulações computacionais. [falta complementar]

Osciladores Lineares Acoplados

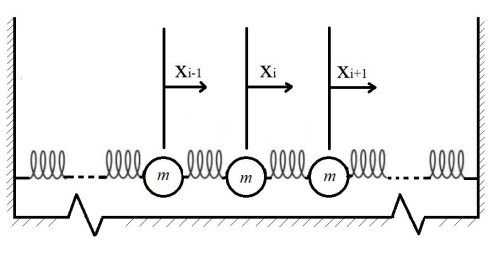
Um modelo geral de sistema unidimensional de osciladores lineares acoplados é ilustrado pela Figura 1. Para fins de simplificação do problema, estamos considerando que todas as massas e constantes das molas são iguais, mas esse não precisaria ser o caso.

Figura 1. Ilustração de um modelo geral unidimensional de oscilações acopladas. A figura foi criada por Paula Pandolfo, uma das integrantes do grupo.

Cada partícula possui duas vizinhas, com as quais interage por meio das molas, exceto as partículas localizadas nos extremos da cadeia, que possuem apenas uma partícula vizinha cada. As interações das partículas dos extremos das cadeias se restringem, portanto, à interação com uma vizinha e com uma mola conectada a uma das paredes externas à cadeia. A posição de cada partícula pode ser descrita por um grau de liberdade associado ao deslocamento em relação à respectiva posição de equilíbrio. No total, um sistema com $N$ partículas terá, portanto, $N$ graus de liberdade. Vamos tratar aqui o caso em que as forças das molas são lineares, i.e., dadas por $F=-kx$.

N=2

Vamos inicialmente considerar o caso do oscilador linear acoplado mais simples, com duas partículas ($N=2$), cada uma com massa $m$, e três molas com os mesmos valores de constantes, $k$.

As equações de movimento do sistema são:

${\begin{aligned}m{\ddot {x}}_{1}&=-kx_{1}-k(x_{1}-x_{2})\\m{\ddot {x}}_{2}&=-kx_{2}-k(x_{2}-x_{1})\quad (1)\\\end{aligned}}$

Uma forma direta de se montar as equações de movimento de um sistema acoplado é pensar em termos dos deslocamentos em relação às posições de equilíbrio ($x_{i}$, com $i=1,2$, no sistema considerado aqui). Por exemplo, na primeira das equações acima, a partícula 1 está sujeita à força elástica da mola conectada à parede (termo $-kx_{1}$) e à força da mola conectada à partícula 2 (termo $-k(x_{1}-x_{2}$). Esse último termo é definido conforme o seguinte: caso a mola que está conectada às partículas 1 e 2 esteja comprimida, $x_{1}$ deve ser maior que $x_{2}$ (definindo os $x_{i}$ como deslocamentos em relação à posição de equilíbrio positivos para a direita e negativos para a esquerda) e a partícula 1 estará sofrendo uma força que é contrária à compressão, ou seja, com sinal negativo. De modo semelhante para a partícula 2, mas nesse caso, devido à posição ocupada pela partícula 2 na cadeia, com $x_{1}$ maior que $x_{2}$, o sentido da força contrária à compressão tem sinal positivo.

Uma dificuldade imposta para a resolução do sistema (1) é o fato das equações serem acopladas: note-se que a aceleração da partícula 1 depende da posição da partícula 2, e vice-versa. Vamos supor que esse sistema de equações tenha soluções nas formas:

${\begin{aligned}x_{1}(t)&=B_{1}e^{-i\omega t}\\x_{2}(t)&=B_{2}e^{-i\omega t}\quad (2)\end{aligned}}$

$B_{1}$ e $B_{2}$ são constantes. Essa suposição é fisicamente justificável: sabemos que as soluções são oscilatórias, e exponenciais imaginárias podem ser escritas em termos de senos e cossenos pela fórmula de Euler. Se substituirmos a equação (2) na equação (1) e rearranjarmos os termos, obtemos:

${\begin{aligned}-mw^{2}B_{1}e^{-i\omega t}+2kB_{1}e^{-i\omega t}-kB_{1}e^{-i\omega t}&=0\\-mw^{2}B_{2}e^{-i\omega t}+2kB_{2}e^{-i\omega t}-kB_{2}e^{-i\omega t}&=0\\\end{aligned}}$

Ou, eliminando as exponenciais e reagrupando termos:

${\begin{aligned}(2k-mw^{2})&B_{1}&-kB_{2}&=0\\-k&B_{1}&+(2k-mw^{2})B_{2}&=0\quad (3)\\\end{aligned}}$

O sistema de equações (3) apenas terá soluções não triviais se o determinante dos coeficientes dos $B_{i}$ for igual a zero, i.e.:

${\begin{vmatrix}(2k-mw^{2})&-k\\-k&(2k-mw^{2})\end{vmatrix}}=0$

As soluções da equação acima podem ser facilmente obtidas e resultam de uma equação quadrática simples, apresentaremos apenas o resultado:

${\begin{aligned}\omega _{1}={\sqrt {\frac {k}{m}}}\quad \quad \omega _{2}={\sqrt {\frac {3k}{m}}}\end{aligned}}$

$\omega _{1}$ e $\omega _{2}$ são as frequências características ou autofrequências do sistema.

Bibliografia principal

• Stephen T. Thornton, Jerry B. Marion, "Classical Dynamics of Particles and Systems". Thomson Learning, Belmont, 2004.
• Giordano, N.J., Nakanishi, H. "Computational Physics". 2nd Edition. Prentice Hall, Upper Saddle River, 2006.