Equação de Águas Rasas
Em construção
Grupo: Gabriel Schmökel e Julia Remus
Introdução
Tsunami é um fenômeno da natureza caracterizado por uma sucessão de ondas marinhas, que devido ao seu grande volume e alta velocidade, podem se tornar catastróficas ao atingir a costa. Sismos, erupções vulcânicas, deslizamentos de terra, impactos e outros movimentos submarinos são a causa para a formação deste evento, sendo a grande maioria provocado pelos movimentos das placas tectônicas.
Formação de um Tsunami
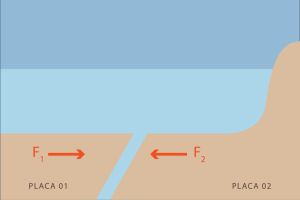
Vamos analisar a sequência de passos da formação de uma Tsunami formada a partir de um abalo sísmico. [1]
I. A convergência das placas tectônicas, devido as correntes de convecção, faz com que existam forças de tensão entre as placas.
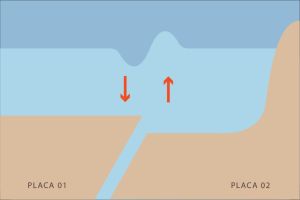
A tensão entre as placas eventualmente ultrapassa o limite máximo, o que provoca o deslizamento brusco de uma das placas sobre a outra, gerando um grande deslocamento de volume de água na vertical. Como a tsunami ocorre em grandes profundidades, ela pode passar despercebida para um barco que navega nas proximidades, uma vez que amplitude da onda é menor.
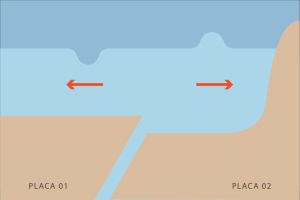
II. A onda gerada se propaga ao longo de todas as direções do plano da água.
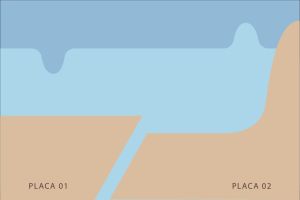
III. A medida que a onda se aproxima da superfície ela diminui sua velocidade e aumenta sua amplitude
Temos o interesse de descrever fisicamente a propagação da Tsunami de acordo com a topografia da água e do mar, por essa razão não iremos estudar o efeito físico que causou o deslocamento do volume de água.
Descrição Física
As equações de águas rasas são as equações físicas que descrevem o fenômeno do Tsunami, em uma dimensão elas são dadas por:
Na representação do fluxo de corrente estas equações se tornam:
As componentes da equação de águas rasas podem ser melhor interpretadas através da seguinte figura:
corresponde a amplitude da onda, determina a profundidade do mar em repouso, é o deslocamento total da água, é a velocidade do fluído e é o fluxo de descarga.
Teoria
Derivação das Equações de Águas Rasas
Para obter as equações de águas rasas devemos partir da equação da continuidade e das equações da quantidade de movimento de Navier-Stokes:
é a densidade; p é a pressão; é o vetor velocidade do fluído, onde u,v e w são as velocidades das partículas que compõe o fluído nas direções x,y,z; é o vetor aceleração da gravidade; é o tensor tensão, onde as componentes deste tensor são as tensões normais e tangenciais de cisalhamento, expressas por , no qual indica a direção e o plano normal.
Introduzindo as condições de contorno [2] para a superfície Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z(x,y,t) } e para a profundidade do oceano Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x,y) } :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{D \eta}{Dt} = \frac{\partial \eta}{\partial t} +\mathbf{v} . \nabla \eta = w } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z= \eta(x,y,t) \qquad (7) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u} . \nabla (z + h(x,y)) = 0 } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z =-h(x,y) \qquad (8)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } é o deslocamento vertical da água sobre a superfície em repouso, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{v} = (x,y,0) } é o vetor velocidade do fluído nas direções horizontais x e y.
A equação da continuidade em (5) pode ser simplificada, já que a densidade do fluído no oceano Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho } não varia significativamente com o tempo e a posição.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \mathbf{u} = 0 \qquad (9) }
Integrando a expressão da continuidade em (9), utilizando a regra da integral de Leibniz [3], com os limites indo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -h(x,y) } até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta (x,y,t) } chegamos na seguinte expressão:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-h}^{\eta} \nabla . \mathbf{u} = \int_{-h}^{\eta} \Big(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}\Big)dz = \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz +w \Big |_{-h}^{\eta} + \mathbf{u} . \nabla (z + h(x,y)) \Big |_{-h}^{\eta} -u \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial x} -v \Big |_{-h}^{\eta} \frac{\partial \eta}{\partial y} \qquad (10) }
Teorema de Leibniz:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{dx} \left (\int_{a(x)}^{b(x)} f(x,t)\,dt \right )= f\big(x,b(x)\big)\cdot \frac{d}{dx} b(x) - f\big(x,a(x)\big)\cdot \frac{d}{dx} a(x) + \int_{a(x)}^{b(x)}\frac{\partial}{\partial x} f(x,t) \,dt \qquad (11)}
Substituindo as condições de contorno da profundidade (8) em (10) obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz - w \Big |_{eta} -\mathbf{v} . \nabla \eta = 0 \qquad (12) }
Substituindo a condição de contorno da superfície (7) em (12):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz + \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz + \frac{\partial \eta}{\partial t} = \frac{\partial u (\eta + h)}{\partial x}+ \frac{\partial v (\eta + h)}{\partial y} + \frac{\partial \eta}{\partial t} = \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} + \frac{\partial \eta}{\partial t} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (13) }
(13) é a primeira das equações das águas rasas que obtemos, onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D } é o comprimento da água total do fundo do oceano até a amplitude da onda. Podemos expressar (13) através do fluxo de descarga nas direções x e y, estás quantidades estão relacionadas com as velocidades da seguinte forma [4]:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = \frac{\partial}{\partial x} \int_{-h}^{\eta} u dz = uD \qquad (14) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \frac{\partial}{\partial y} \int_{-h}^{\eta} v dz = vD \qquad (15) }
Substituindo (14) e (15) em (13) chegamos na representação do fluxo de descarga para uma das equações de águas rasas.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial \eta}{\partial t} + \frac{\partial M}{\partial x}+ \frac{\partial N}{\partial y} = 0 \qquad (16) }
Escrevendo as quantidades de movimento de Navier-Stokes nas componentes x,y e z:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_x = 0 \qquad (17) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_y = 0 \qquad (18) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\frac{\partial P}{\partial x} +g_z = 0 \qquad (19) }
Na componente z em (19) negligenciamos a aceleração das partículas, pois a aceleração da gravidade é muito maior. Também tomamos como nulos as componentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_y} em (17) e (18), passamos a definir Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_z = g } .
Resolvendo equação diferencial da componente z em (19) podemos obter a pressão, a qual é hidrostática.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial P = \rho g \partial z \Rightarrow P = \rho g (\eta - z) \qquad (20) }
Substituindo a pressão em (17):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} +g \frac{\partial \eta}{\partial x} =0 \qquad (21) }
Integrando a expressão (21), utilizando a regra da integral de Leibniz e as condições de contorno (7) e (8), com os limites indo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -h(x,y)} até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta(x,y,t)} chegamos em outra das equações de águas rasas:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial uD}{\partial t} + \frac{\partial u^{2}D}{\partial x} + \frac{\partial uvD}{\partial y} + \frac{g}{2} \frac{\partial D^2}{\partial x} =0 \qquad (22) }
Generalizando a equação (22), para a componente y, obtemos a última das equações de águas rasas:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial vD}{\partial t} + \frac{\partial v^{2}D}{\partial y} + \frac{\partial uvD}{\partial x} + \frac{g}{2} \frac{\partial D^2}{\partial y} =0 \qquad (23) }
Na representação de fluxo de cargas as expressões (22) e (23) são apresentadas respectivamente como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} = 0 \qquad (24) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} = 0 \qquad (25) }
Iremos escrever as equações das águas rasas considerando o tensor de estresse Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\tau} } . Os elementos deste tensor são responsáveis por causar nas partículas tensões tangenciais e perpendiculares, onde as tensões tangenciais são representadas por elementos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{ij}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \ne j } , e as perpendiculares por elementos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{ij}} onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = j }
Decompondo nas componentes x,y, e z de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho} \nabla . \boldsymbol{\tau} } presente em (6):
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) \qquad (26) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{yx} + \frac{\partial}{\partial y} \tau_{yy} + \frac{\partial}{\partial z}\tau_{yz} \Big) \qquad (27) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{zx} + \frac{\partial}{\partial y} \tau_{zy} + \frac{\partial}{\partial z}\tau_{zz} \Big) \qquad (28) }
Considerando o fluído Newtoniano, então as tensões de cisalhamento serão proporcionais a uma taxa de deformação, onde a constante de deformidade é a viscosidade.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{xy} = \tau_{yx} = \mu \Big( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \Big) \qquad (29) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{xz} = \tau_{zx} = \mu \Big( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \Big) \qquad (30) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{yz} = \tau_{zy} = \mu \Big( \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \Big) \qquad (31) }
Substituindo (29),(30) em (26), integrando em relação a componente z, utilizando a regra de Leibnz e as condições de contorno (7) e (8), obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-h}^{\eta} \frac{1}{\rho}\Big(\frac{\partial}{\partial x} \tau_{xx} + \frac{\partial}{\partial y} \tau_{xy} + \frac{\partial}{\partial z}\tau_{xz} \Big) = \frac{\tau_x}{\rho} -A \Big ( \frac{\partial^{2}}{\partial x^{2}}M \frac{\partial^{2}}{\partial x^{2}} M \Big) \qquad (32) }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } é a constante de viscosidade turbulenta, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_x } é uma força de resistividade relativa ao movimento do fluído com o fundo do oceano na direção x. Podemos negligenciar a constante de turbulência na situação em que não temos inclinações abrutas no fundo do mar. [5]
Considerando que o fluído é uniforme, então a expressão para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} é } é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} = \frac{fM}{2D^{2}}(M^{2}+N^{2})^{1/2} \qquad (33) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } é o coeficiente de fricção, porém o coeficiente de rugosidade de Manning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } é mais usado, alguns valores deste coeficiente são: [6]
| Material | Coeficiente de Rugosidade de Manning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (n) } |
|---|---|
| Cimento puro e metal liso | 0,010 |
| Terra lisa | 0,017 |
| Pedras, ervas daninhas | 0,035 |
| Péssimo relevo de canal | 0,060 |
| Bom relevo de canal | 0,025 |
O coeficiente de fricção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } e o de rugosidade de Meanning Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } estão relacionados por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \frac{2gn^{2}}{D^{1/3}} \qquad (34) }
Substituindo (34) em (33) obtemos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_x}{\rho} = \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (35) }
Generalizando a expressão (31) para a componente y. Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\tau_y}{\rho} = \frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} \qquad (36) }
Adicionando, repectivamente, (35) e (36) nas expressões (24) e (26), obtemos as equações de águas rasas considerando as forças de fricção do fundo do oceano.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M}{\partial t} + \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x} + \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} = 0 \qquad (37) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N}{\partial t} + \frac{\partial }{\partial y}\Big(\frac{N^{2}}{D}\Big) + \frac{\partial }{\partial x}\Big(\frac{MN}{D}\Big) +gD \frac{\partial \eta}{\partial x} +\frac{gn^{2}}{D^{7/3}} N(M^2 +N^2)^{1/2} = 0 \qquad (38) }
Forma Conservativa
Um modelo mais simples - desconsiderando a fricção, viscosidade do líquido e as forças de Coriolis sobre ele - pode ser obtido [7][8]. Para desenvolvê-lo são necessárias algumas premissas:
- O comprimento da onda é muito maior que as contribuições na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}}
- A aceleração na direção da velocidade na direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}} é zero
- As componentes das velocidades em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} e em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{y}} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}} ) não variam em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{z}}
O sistema então pode ser descrito pelas seguintes equações:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial h}{\partial t} + \dfrac{\partial hu}{\partial x} + \dfrac{\partial hv}{\partial y} = 0 \qquad (39) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial hu}{\partial t} + \dfrac{\partial \left ( hu^2 + \dfrac{1}{2}g h^2 \right)}{\partial x} + \dfrac{huv}{\partial y} = -gh\dfrac{\partial b}{\partial x} \qquad (40) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial hv}{\partial t} + \dfrac{huv}{\partial x} + \dfrac{\partial \left ( hv^2 + \dfrac{1}{2}g h^2 \right)}{\partial y}= -gh\dfrac{\partial b}{\partial y}\qquad (41) }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} é a altura do fluido desde a base, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}, \vec{v}} são as velocidades médias na direções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}, \vec{y}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} é a constante gravitacional e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b(x, y)} é função que descreve a superfície onde acontece o movimento [3].
Para descrever numericamente as equações de águas rasas na forma conservativa foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{h^{t + \Delta t}_{i, j} - h^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(hu)^t_ {i+1,j} - (hu)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(hv)^t_ {i,j+1} - (hv)^t_{i, j-1}}{2 \Delta y} \right ] = 0 \qquad (42)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{hu)^{t + \Delta t}_{i, j} - (hu)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(hu^2 + \cfrac{1}{2}gh^2)^t_{i+1, j} - (hu^2 + \cfrac{1}{2}gh^2)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(huv)^t_{i, j+1} - (huv)^t_{i, j-1}}{2 \Delta y} \right ] = -g h^{t}_{i, j} b_{x. i, j} \qquad (43) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{(hv)^{t + \Delta t}_{i, j} - (hv)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(huv)^t_{i+1, j} - (huv)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(hv^2 + 1/2 gh^2)^t_{i, j+1} - (hv^2 + 1/2 gh^2)^t_{i, j-1}}{2 \Delta y} \right ] = -g h^{t}_{i, j} b_{y. i, j} \qquad (44) }
Forma dissipativa
As equações de águas rasas na forma não conservativa são dadas por (10),(33) e (34). Para descrever numericamente o fenômeno foi utilizado discretização por diferenças finitas, onde realizamos derivadas centradas na região espacial, e para frente no região temporal. O erro de truncamento é de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \mathcal{O}(x^2) } na região espacial, enquanto na temporal é de ordem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \mathcal{O}(t^1) } . O método é conhecido como leap-frog method devido a discretização central na região espacial.
Discretizando a expressão (10) pelo leap-frog method:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \eta}{\partial t} + \frac{\partial uD}{\partial x}+ \frac{\partial vD}{\partial y} = 0 \qquad (36) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\eta(x,y,t + \Delta t) - \eta(x,y,-t)}{\Delta t} = - \frac{M(x + \Delta x,y,t) - M(x- \Delta x,y,t)}{2\Delta x} -\frac{N(x,y+ \Delta x,t) - N(x,y - \Delta y,t)}{2\Delta y} \qquad (37) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{i,j}^{n+1} = n_{i,j}^{n} -\Delta t\Bigg(\frac{M_{i+1,j}^{n}-M_{i-1,j}^{n}}{2\Delta x} + \frac{M_{i,j+1}^{n}-M_{i,j-1}^{n}}{2\Delta y} \Bigg) \qquad (38) }
Discretizando a expressão (33) pelo leap-frog method:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{\partial M}{\partial t} = -\Bigg( \frac{\partial }{\partial x}\Big(\frac{M^{2}}{D}\Big) + \frac{\partial }{\partial y}\Big(\frac{MN}{D}\Big)+ gD \frac{\partial \eta}{\partial x}+ \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \Bigg) \qquad (39) }
Definindo as quantidades:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M2 \equiv \frac{M^2(x,y,t)}{D(x,y,t)}\qquad (40) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle MN \equiv \frac{M(x,y,t)N(x,y,t)}{D(x,y,t)} \qquad (41) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y,t) \equiv \frac{gn^{2}}{D^{7/3}} M(M^2 +N^2)^{1/2} \qquad (42) }
Das quantidades definidades e da derivada parcial do fluxo de descarga em relação ao tempo temos a respectiva avanço temporal para M:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{i,j}^{n+1} = M_{i,j}^{n} -\Delta t \Bigg( \frac{M2_{i+1,j}^n-M2_{i-1,j}^n}{2 \Delta x} +\frac{(MN)_{i,j+1}^n - (MN)_{i,j-1}^n}{2 \Delta y} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta x} +f_{i,j}^{n}\Bigg) \qquad (43) }
Generalizando a expressão (43) para o fluxo de descarga N temos:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{i,j}^{n+1} = N_{i,j}^{n} -\Delta t \Bigg( \frac{N2_{i,j+1}^n-M2_{i,j-1}^n}{2\Delta y} +\frac{(MN)_{i+1,j}^n - (MN)_{i-1,j}^n}{2\Delta x} +gD_{i,j}^{n} \frac{\eta_{i+1,j}^{n} - \eta_{i-1,j}^{n}}{2\Delta y} +f_{i,j}^{n}\Bigg) \qquad (44) }
Simulações Computacionais de Tsunamis
Solução em 1D
Para a solução em uma direção foi utilizado os mesmos códigos abaixo descritos, desconsiderando a contribuição da direção Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{y}} . Após a descrição dos programas desenvolvidos, será apresentada uma comparação entre ele e o 2D (conservativo e dissipativo).
Forma conservativa 2D
Para descrever numericamente o fenômeno foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{h^{t + \Delta t}_{i, j} - h^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(hu)^t_ {i+1,j} - (hu)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(hv)^t_ {i,j+1} - (hv)^t_{i, j-1}}{2 \Delta y} \right ] = 0}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{hu)^{t + \Delta t}_{i, j} - (hu)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(hu^2 + \cfrac{1}{2}gh^2)^t_{i+1, j} - (hu^2 + \cfrac{1}{2}gh^2)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(huv)^t_{i, j+1} - (huv)^t_{i, j-1}}{2 \Delta y} \right ] = -g h^{t}_{i, j} b_{x. i, j}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{(hv)^{t + \Delta t}_{i, j} - (hv)^{t}_{i, j}}{\Delta t} + \left [ \dfrac{(huv)^t_{i+1, j} - (huv)^t_{i-1, j}}{2 \Delta x} \right ] + \left [ \dfrac{(hv^2 + 1/2 gh^2)^t_{i, j+1} - (hv^2 + 1/2 gh^2)^t_{i, j-1}}{2 \Delta y} \right ] = -g h^{t}_{i, j} b_{y. i, j} }
Para os contornos foi utilizado que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x_f, y) = - u(x_f - \Delta x, y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x_i, y) = - u(x_i + \Delta x, y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x, y_f) = - v(x, y_f - \Delta y)}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x, y_i) = - v(x, y_i + \Delta y)}
- Nos contornos de x: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\partial h}{\partial x} = 0} , discretizando essa derivada temos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{i(+/-)1, j} = h_{i, j}}
- Nos contornos de y: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\partial h}{\partial y} = 0} , discretizando essa derivada temos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{i, j(+/-)1} = h_{i, j}}
Código
O código foi escrito na linguagem Python.
#%% Bibliotecas
import numpy as np
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
import matplotlib.patches as mpatches
from IPython.display import HTML, Image
#%% Parametros
L_xf = 10.0 # m
L_x0 = -L_xf
NX = 100
dx = (L_xf - L_x0) / NX
L_yf = 10.0 # m
L_y0 = -L_yf
NY = 100
dy = (L_yf - L_y0) / NY
N_INNER = (NX - 2) * (NY - 2)
g = 9.8 # m /s^2
# Tempo
dt = 0.002
Nt = 1500
time_interval = np.arange(0, Nt*dt, dt)
#%% Discretização do espaço x-y
x = np.linspace(L_x0, L_xf, NX-1)
y = np.linspace(L_y0, L_yf, NY-1)
X, Y = np.meshgrid(x, y)
#%% Condições iniciais, em distribuição gaussiana
sigma = 1.0
sigma_v = 1.0
h_2d = 5 * np.ones(shape=np.shape(X)) + np.exp(-(((X)**2 / 2*(sigma**2)) + ((Y)**2 / 2*(sigma**2))))
u_2d = 0.1 * np.exp(-(((X)**2 / 2*(sigma_v**2)) + ((Y)**2 / 2*(sigma_v**2))))
v_2d = 0.1 * np.exp(-(((X)**2 / 2*(sigma_v**2)) + ((Y)**2 / 2*(sigma_v**2))))
#%% Vetores das variáveis anteriores e historico das variaveis
h_ant = np.copy(h_2d)
v_ant = np.copy(v_2d)
u_ant = np.copy(u_2d)
# Inicilização das listas para armazenar os valores
hist_h, hist_u, hist_v = [], [], []
Função para resolução das equações diferenciais com FTCS.
# Fator de multiplicacao
fator_x = (dt / (2*(dx)))
fator_y = (dt / (2*(dy)))
def resolve_pdes(h, vx, vy):
"""
Função que retorna os valores de profunidade, velocidade em x e em y
no próximo tempo
Parametros
-----------
h : float
profundidade no tempo t
vx : float
velocidade em x no tempo t
vy : float
velocidade em y no tempo t
Retorna
-----------
prox_h : float
profundidade no tempo t + dt
prox_u : float
velocidade em x no tempo t + dt
prox_v : float
velocidade em y no tempo t + dt
"""
# Inicializa os vetores para armazenarem os resultados calculados
prox_h = np.ones(shape = (np.shape(h)), dtype = np.float64)
prox_u = np.ones(shape = (np.shape(vx)), dtype = np.float64)
prox_v = np.ones(shape = (np.shape(vy)), dtype = np.float64)
# Loop nos pontos discretizados
for i in range(1, NX - 1):
for j in range(1, NY - 1):
# Alturas e velocidades conforme a posicao do ponto:
# _l : ponto a esquerda, _r: ponto a direita, _up: ponto acima, _d: abaixo
# Condicao a esquerda ------------------
if i == 1: # primeiro x interno
h_l = h[i, j]
u_l = -vx[i, j]
v_l = vy[i, j]
else:
h_l = h[i-1, j]
u_l = vx[i-1, j]
v_l = vy[i-1, j]
# --------------------------------------
# Condicao a direita -------------------
if i == NX - 2: # ultimo x interno
h_r = h[i, j]
u_r = -vx[i, j]
v_r = vy[i, j]
else:
h_r = h[i+1, j]
u_r = vx[i+1, j]
v_r = vy[i+1, j]
# --------------------------------------
# Condicao abaixo ----------------------
if j == 1: # primeiro y interno
h_d = h[i, j]
u_d = vx[i, j]
v_d = - vy[i, j]
else:
h_d = h[i, j - 1]
v_d = vy[i, j - 1]
u_d = vx[i, j - 1]
# --------------------------------------
# Condicao acima ----------------------
if j == NY - 2: # utlimo y interno
h_up = h[i, j]
u_up = vx[i, j]
v_up = - vy[i, j]
else:
h_up = h[i, j + 1]
v_up = vy[i, j + 1]
u_up = vx[i, j + 1]
# --------------------------------------
## Primeira Equação
h_ij = h[i, j] - \
(h_r * u_r - h_l * u_l) * fator_x - \
(h_up * v_up - h_d * v_d) * fator_y
prox_h[i, j] = h_ij
# ## Segunda equação
hu_ij = ((h[i, j]) * vx[i, j]) - \
fator_x * (
((h_r * (u_r ** 2)) + (1/2 * g * (h_r ** 2))) -\
((h_l * (u_l ** 2)) + (1/2 * g * (h_l ** 2)))
) - fator_y * (
(h_up * u_up * v_up ) - (h_d * u_d * v_d)
)
# # ## Terceira Equação
hv_ij = (h[i, j] * vy[i, j]) - \
fator_x * (
(h_r * u_r * v_r) - (h_l * u_l * v_l)
) - \
fator_y * (
((h_up * (v_up ** 2)) + (1/2 * g * (h_up ** 2))) - \
((h_d * (v_d ** 2)) + (1/2 * g * (h_d ** 2)))
)
prox_v[i, j] = hv_ij / (h_ij)
return prox_h, prox_u, prox_v
#%% Cálculo
# Resolve para cada passo de tempo
for t in time_interval:
h, u, v = resolve_pdes(h_ant, u_ant, v_ant) # valores das variaveis no tempo = t + dt
# faz isso pq tava dando um erro estranho nesses pontos?
h[0, :] = h[1, :]
h[:, 0] = h[:, 1]
v[0, :] = v[1, :]
v[:, 0] = v[:, 1]
u[0, :] = u[1, :]
u[:, 0] = u[:, 1]
# adicionar essas variáveis em listas pra conseguir plotar dps
hist_h.append(h); hist_u.append(u); hist_v.append(v)
# Coloca as variaveis atuais como anteriores pro proximo calculo
h_ant = np.copy(h)
u_ant = np.copy(u)
v_ant = np.copy(v)
#%% Gráfico
# Reorganiza os vetores para plotar
x_2d = X[0]
y_2d = Y[0]
for i in range(1,len(X)):
x_2d = np.append(x_2d, X[i])
y_2d = np.append(y_2d, Y[i])
def animate(i):
plt.clf() # limpa a figura, pra nao ficar sobrepondo figs
# titulos
plt.suptitle('Evolução da onda', fontsize=14)
plt.title(f'Tempo: {round(dt*i, 3)}', fontsize=12)
# labels
plt.ylabel('y', fontsize=8)
plt.xlabel('x', fontsize=8)
# plot
graph = plt.scatter(x_2d, y_2d, c= hist_h[0::8][i], vmin=4.5, vmax=5.5, marker='.')
plt.colorbar()
plt.savefig(f'caminho-frames/{i}.png')
return graph
# fig = plt.figure(figsize=(16,9))
# ax = fig.gca(projection='3d')
fig, ax = plt.subplots()
ani = animation.FuncAnimation(fig, animate, frames = len(hist_h[0::8]), repeat=False, interval=0.1)
#%% Salva o gif, com os frames salvos anteriormente
images = []
for i in range(len(hist_h[0::80])):
images.append(imageio.imread(f'caminho-frames/{i}.png'))
imageio.mimsave("gif2.gif", images,fps=8)
Resultados
Exemplo 1. Onda confinada em uma caixa: utilizando que a superfície é constante e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço, obtemos a evolução no espaço que pode ser vista no GIF abaixo.
Forma dissipativa 2D
Os exemplos que seguem utilizam as equações de ondas rasas (38),(43) e (44) para calcular os passos de tempo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } , onde as funções em python atualiza_eta, atualiza_M, e atualiza_N implementam computacionalmente isto. Para implementar estas funções e outras ideias do nosso programa, o seguinte código fonte da referência [9] foi usado como base.
def atualiza_eta(eta, M, N, dx, dy, dt, nx, ny):
for j in range(1,nx-1):
for i in range(1,ny-1):
dMdx = (M[j+1,i] - M[j-1,i]) / (2. * dx)
dNdy = (N[j,i+1] - N[j,i-1]) / (2. * dy)
eta[j, i] = eta[j, i] - dt * (dMdx + dNdy)
#Condições de contorno do problema
eta[0,:] = eta[1,:]
eta[-1,:] = eta[-2,:]
eta[:,0] = eta[:,1]
eta[:,-1] = eta[:,-2]
return eta
def atualiza_M(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny):
M2 = M **2 / D
MN = M * N / D
fric = g * n**2 * M * np.sqrt(M**2 + N**2) / D**(7./3.)
for j in range(1,nx-1):
for i in range(1,ny-1):
dM2dx = (M2[j+1,i] - M2[j-1,i]) / (2. * dx)
dMNdy = (MN[j,i+1] - MN[j,i-1]) / (2. * dy)
dETAdx = (eta[j+1,i] - eta[j-1,i]) / (2. * dx)
M[j, i] = M[j, i] - dt * (dM2dx + dMNdy + g * D[j,i] * dETAdx + fric[j,i])
return M
def atualiza_N(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny):
MN = M * N / D
N2 = N**2 / D
fric = g * n**2 * N * np.sqrt(M**2 + N**2) / D**(7./3.)
for j in range(1,nx-1):
for i in range(1,ny-1):
dMNdx = (MN[j+1,i] - MN[j-1,i]) / (2. * dx)
dN2dy = (N2[j,i+1] - N2[j,i-1]) / (2. * dy)
dETAdy = (eta[j,i+1] - eta[j,i-1]) / (2. * dy)
N[j, i] = N[j, i] - dt * (dMNdx + dN2dy + g * D[j,i] * dETAdy + fric[j,i])
return N
A função shallow water waves recebe os parâmetros iniciais do nosso programa, executa o Loop responsável pela atualização das variáveis da amplitude da onda e do fluxo de descarga com o tempo, através da chamada das funções atualiza M,N e eta. Posteriormente, a cada passagem dentro do loop um plot do sistema é feito. Obs: não colocamos todo código da função shallow_water na imagem a seguir, apenas a que mencionamos neste parágrafo.
def shallow_water(eta0, M0, N0, h, g, n, nt, dx, dy, dt, X, Y):
eta = eta0.copy()
M = M0.copy()
N = N0.copy()
D = eta + h
# ...
for k in range(1,nt):
eta = atualiza_eta(eta, M, N, dx, dy, dt, nx, ny)
M = atualiza_M(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny)
N = atualiza_N(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny)
D = eta + h
fig = plt.figure(figsize=(8.,6.))
fundo = plt.imshow(-h, 'Purples', interpolation = 'nearest', extent = limites)
amp = plt.imshow(eta, extent = limites, interpolation = 'sinc', cmap = 'seismic', alpha= 0.75, vmin=-0.4, vmax= 0.4)
#plt.title('tempo = %f', dt*n )
#plt.plot(f'Tempo {round(k*dt,3)} s')
plt.xlabel('x [m]')
plt.ylabel('y [m]')
cbar_amp = plt.colorbar(amp)
cbar_fundo = plt.colorbar(fundo)
cbar_fundo.set_label(r'$-h$ [m]')
cbar_amp.set_label(r'$\eta$ [m]')
plt.show()
Exemplo 1 - Tsunami Confinada em uma Caixa
Exemplo 2.1 - Tsunami Propagando-se em Direção a Praia
Exemplo 2.2 - Tsunami Propagando-se em Direção a Praia
Comparação entre Métodos
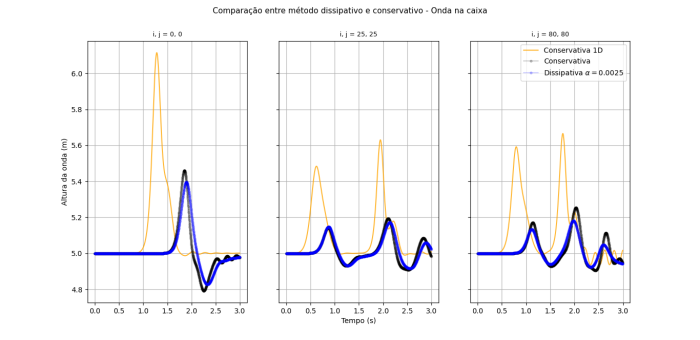
Onda confinada em uma caixa
Abaixo é mostrado o gráfico de evolução temporal da altura da onda em três pontos distintos do sistema. Pode-se perceber que com o passar do tempo o movimento das duas equações começa a divergir, mesmo com o fator de fricção baixo.
Para o método 1D é de se esperar que exista menos interferências entre as ondas, pois só existe parede nos finais do sistema, além disso, a onda só precisa se espalhar em uma direção, então a sua amplitude é maior.
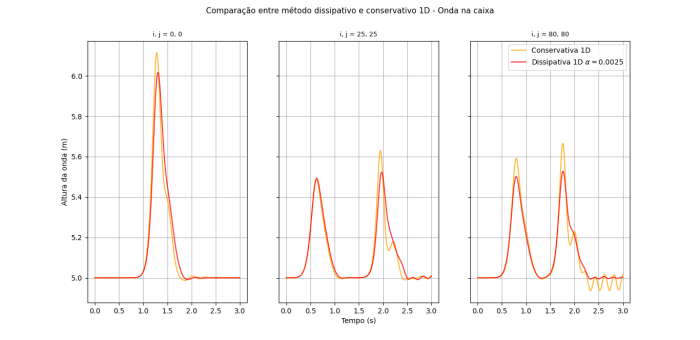
Também é possível perceber a diferença entre métodos observando apenas em uma direção (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} ).
Referências
- ↑ HOW EARTHQUAKES TRIGGER TSUNAMIS-BBC. British Broadcasting Corporation. Disponível em: https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html
- ↑ SEGUR, Harvey; YAMAMOTO, Hiroki. Lecture 8: The Shallow-Water Equations.Disponível em: <https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html>
- ↑ 3,0 3,1 https://en.wikipedia.org/wiki/Leibniz_integral_rule Erro de citação: Etiqueta inválida
<ref>; Nome "Hopf" definido várias vezes com conteúdo diferente - ↑ IMAMURA, Fumihiko.Tsunami Modelling Manual.Disponível em: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf
- ↑ http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf
- ↑ LINSLEY, Ray K.; FRANZINI, Joseph B. Water Resources Engineering.
- ↑ GARCÍA-NAVARRO, P; et al. The shallow water equations: An example of hyperbolic system. Espanha: 2008. Disponível em: <https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.571.1364&rep=rep1&type=pdf>
- ↑ KUHBACHER, Christian. Shallow Water: Derivation and Applications. Disponível em: <http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/Kuehbacher2009.pdf>
- ↑ KOEHN, Daniel. 2D Shallow Water Equations. Disponível em: <https://github.com/daniel-koehn/Differential-equations-earth-system/blob/master/10_Shallow_Water_Equation_2D/01_2D_Shallow_Water_Equations.ipynb>