Modelo de agentes de distribuição de riquezas
Grupo: Bernardo Boatini, Murilo Kessler Azambuja e Natália Ferrazzo
Introdução
A física estatística, em particular a teoria cinética dos gases, fornece uma estrutura útil para descrever a complexidade das interações de mercado. Da mesma forma que um sistema físico composto de muitas partículas trocando energia via colisões binárias, os Modelos de Troca de Cinética consideram um conjunto de agentes econômicos interagentes que trocam de forma binária uma quantidade conservada chamada de riqueza.
Este trabalho tem como objetivo calcular a evolução temporal da distribuição de riqueza entre entre um certo numero de agentes, utilizando diferentes regras de interação e um critério para medir quantitativamente a desigualdade de econômica no sistema.
Modelo
Vamos supor um sistema com agentes, onde o agente é caracterizado pela riqueza e pelo fator de aversão-a-riscos no tempo . Podemos então definir uma troca de riqueza entre os agentes e —selecionados aleatoriamente, supondo que ganha uma riqueza de —, como [1]
Em modelos de trocas binárias como esse, mesmo que a regra não favoreça nenhum dos lados, já foi comprovado que o estado final sempre leva a condensação de riqueza em um agente[2], ou seja, máxima desigualdade. Para pensar formas de evita a condensação certas dinâmicas podem ser adicionadas ao problema, como definir uma prefêrcia de troca do mais rico para o agente mais pobre.
Para decidir quem ganha e quem perde riqueza durante a interação entre agentes, utiliza-se uma probabilidade de favorecer o agente mais pobre, evitando assim a condensação, i.e., o acúmulo de toda riqueza disponível em apenas um ou poucos agentes [1]. Esta probabilidade é dada por [1] [3]
onde é chamado de fator de proteção social, que varia de —mesma probabilidade de ganho de riqueza para ambos os agentes— até —máxima probabilidade de favorecer o agente mais pobre—. Desta forma, a probabilidade do agente mais pobre ganhar a quantidade em uma interação entre agentes é , enquanto que a probabilidade do agente mais rico ganhar a mesma quantidade é . Além disso, vemos na equação (1) que quanto maior a desigualdade de riqueza (), maior é a atuação de . Isso nos mostra que o fator de proteção social é uma forma de simular a aplicação políticas sociais que favorecem a distribuição de renda na população.
Uma vez sorteado qual agente ganha e qual perde na interação, deve-se determinar qual será a quantidade a ser trocada por ambos. Existem diversas formas de se determina-la (algumas delas encontram-se de forma detalhada em [2]), porém neste trabalho focaremos na regra do mínimo e na regra do perdedor, enunciadas abaixo.
Regra do Mínimo
Nesta regra, temos que a quantidade de riqueza trocada entre os agentes é definida como [4]
Esta regra muitas vezes também é chamada de regra justa, pois a quantidade de riqueza trocada entre os agentes é a mesma, independente do ganhador, logo nenhum dos agentes é favorecido.
Regra do Perdedor
Neste caso, para tentar evitar condensações, temos que é obtido apenas pela quantia arriscada pelo perdedor, desta forma temos [4]
lembrando que é o agente perdedor. Desta forma, a quantidade de riqueza a ser trocada será sempre proporcional à fortuna de (i.e., ) e regulada por quanto o agente está disposto a arriscar (), tornando a interação entre os agentes muito mais favorável para o perdedor.
Coeficiente de Gini
O Coeficiente de Gini é um índice frequentemente utilizado por economistas e organizações estatísticas para mensurar quantitativamente a desigualdade de distribuição de renda em uma determinada região. Ele é definido como [1]
O índice de Gini varia de 0, quando todos os agentes possuem a mesma riqueza (i.e., desigualdade mínima), até 1, quando toda riqueza está concentrada em apenas um agente (i.e, desiguladade máxima). Este coeficiente é utilizado tanto para medir a desigualdade na distribuição de renda dos agentes da simulação, quanto como uma medida de dispersão, para determinar a estabilidade da distribuição de riqueza [1].
Resultados
Como unidade de tempo das simulações foi utilizado o MCS (Monte Carlo Step), definido como o menor número de passos necessários para que todos os agentes sejam sorteados[1]
Evolução temporal sem fator de proteção social
As simulações que serão apresentadas abaixo foram realizadas com um número de agentes sob uma média entre 10 ensembles diferentes para cada valor de . As condições iniciais em todas simulações foram tais que a riqueza () está inicialmente distribuída no intervalo seguindo uma distribuição aleatória uniforme.
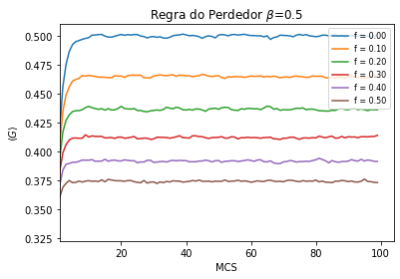
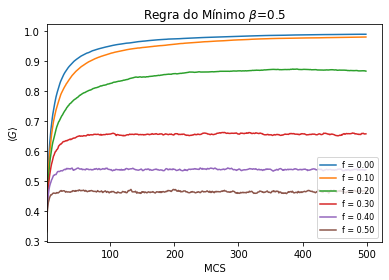
Na Figura 1 e na Figura 2 temos a evolução temporal do coeficiente de Gini para a regra do perdedor e para a regra do mínimo, respectivamente. Note que após um certo número de MCS, o índice de Gini tende a convergir para um valor estável, para cada valor de . O tempo de simulação foi escolhido de forma que o equilíbrio fosse atingido (o primeiro MCS foi ignorado).
Na Figura 2, vemos que o valor de estabilidade do índice de Gini sempre tende para o valor de desigualdade máxima, mesmo se mudarmos o valor de . Desta forma, quando não inserimos um fator de proteção social no problema e assumimos que as trocas entre agentes ocorrem segundo a regra do mínimo, teremos sempre uma condensação da riqueza, levando a uma alta desigualdade econômica.
Por outro lado, na Figura 1, vemos que quanto maior for o fator de aversão-ao-risco, menor será a desigualdade econômica e apenas quando ocorre condensação (indicando, pela equação (3), que em cada interação os agentes irão trocar toda a riqueza disponível para eles).
Este resultado (a regra do mínimo sempre gerar uma condensação enquanto que a regra do perdedor estabiliza em um valor para ) ocorre pois, como o valor de beta é igual para todos os agentes, teremos que, por (3), os agentes com maior riqueza irão perder mais dinheiro na regra do perdedor do que os agentes com menor riqueza e, desta forma, a riqueza estará mais bem distribuída quando o equilíbrio for atingido. Por outro lado, como na regra do mínimo o valor trocado independe de quem perde, se forem sorteados agentes com uma diferença muito grande de riqueza teremos que, por (2), a quantidade de riqueza perdida pelo agente mais pobre será muito maior comparativamente com sua própria riqueza. Desta forma teremos que, após tempo suficiente, a regra do mínimo sempre irá tender para uma distribuição de renda desigual.
Evolução temporal com fator de proteção social
As simulações que serão apresentadas abaixo foram realizadas com um número de agentes sob uma média entre 10 ensembles diferentes para cada valor de a um (escolhido apenas para ilustra uma situação em que todos tem 50% de chance de assumir riscos). As condições iniciais em todas simulações foram tais que a riqueza () está inicialmente distribuída no intervalo seguindo uma distribuição aleatória uniforme.
Na Figura 5 e na Figura 6 temos a evolução temporal do coeficiente de Gini para a regra do perdedor(a esquerda) e para a regra do mínimo(a direita). Note que após um certo número de MCS, o índice de Gini tende a convergir para um valor estável, para cada valor de f e que nem sempre leva a condensação. O tempo de simulação foi escolhido de forma que o equilíbrio fosse atingido (o primeiro MCS foi ignorado).
Além de diminuir o Gini de equilíbrio para todos os
Diagrama ""
Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 https://arxiv.org/pdf/1904.05875.pdf CARDOSO, B. F.;GONÇALVEZ, S.; IGLESIAS, J. R.; "WEALTH DISTRIBUTION MODELS WITH REGULATIONS: DYNAMICS AND EQUILIBRIA"
- ↑ 2,0 2,1 https://www.lume.ufrgs.br/bitstream/handle/10183/217456/001121445.pdf?sequence=1 CARDOSO, B. F.; "A concentração de riqueza em sistemas de
trocas binárias não enviesadas
" Erro de citação: Etiqueta inválida
<ref>; Nome "MESTRADOBENHUR" definido várias vezes com conteúdo diferente - ↑ https://arxiv.org/pdf/cond-mat/0306579.pdf SCAFETTA, N.;WEST, B. J.; PICOZZI, S.; "A Trade-Investment Model for Distribution of Wealth"
- ↑ 4,0 4,1 https://link.springer.com/content/pdf/10.1140/epjst/e2007-00072-4.pdf CAON, G.M.; GONÇALVEZ, S.; CARDOSO, B. F.; "The unfair consequences of equal opportunities: Comparing exchange models of wealth distribution"















![{\displaystyle \Delta w=min[(1-\beta _{i})w_{i}(t);(1-\beta _{j})w_{j}].\qquad (2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84c14ed649fea008d90dbdeed2971dc4781ada97)







![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
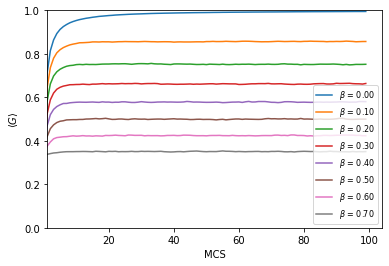
![{\displaystyle \beta \in [0,0.7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/520bab77b30a823b7350b1c3b532a80601369a78)