Análise de Energias DM Microcanônico
Em dinâmica molecular é necessário que se tenha ideia do erro relacionado à limitação computacional que temos em relação à quantidade de partículas que podemos simular em um sistema, ao passo de tempo associado à simulação (dt) e no caso do ensemble microcanônico farei uma análise de como o raio de corte do potencial de Lennard-Jones também pode afetar a energia total do sistema em DM.
Delta t
Para poder mostrar como o comportamento da simulação pode mudar de acordo com o dt associado mostrarei a variância da energia total do sistema (que supostamente deveria 0, pois a energia deveria ser constante). Juntamente com a estrutura do sistema que será mostrado pela g(r).
Função de distribuição radial (g(r)) para um dt de 0.001.
Função de distribuição radial (g(r)) para um dt de 0.01.
Função de distribuição radial (g(r)) para um dt de 0.1.
Variância da energia total do sistema versus o delta t associado na simulação.
Pode-se ver nitidamente que com dt = 0.001 e dt = 0.01 a estrutura do sistema continua sendo a mesma e a variância da energia não tem ainda um valor muito alto. Entretanto nas simulações que eu fiz, para dt > 0.02 a simulação já começa a ficar muito parecida com o caso onde dt = 0.1 e a estrutura do sistema é completamente não física.
Número de Partículas
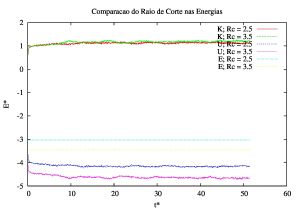
Análise do Raio de Corte
O potencial de Lennard-Jones tem uma contribuição bastante pequena após determinado ponto. Este ponto onde desconsideramos essa contribuição chamamos Raio de corte(Rc). Em muitos livros o raio de corte do potencial de lennard-jones é usado Rc = 2,5. Mas o ponto que quero levantar neste tópico é que mesmo após Rc = 2,5 ele ainda é relevante para o calculo da energia total, potencial e cinética do sistema. Para demonstrar, usei uma densidade constante e 1000 partículas para montar o gráfico abaixo onde é possível notar a contribuição que esse potencial tem sobre o sistema após o Rc = 2,5.
