Simulação de Micélio de Fungo

Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss

O objetivo deste trabalho é modelar computacionalmente o desenvolvimento de micélios em fungos com base em mecanismos gerais pré-estabelecidos. O progresso e a complexidade dos modelos cresceram de maneira gradual ao longo do trabalho através de três modelos de crescimento diferentes. O trabalho foi inspirado - principalmente - nos dois primeiros capítulos do artigo de Steven Hopkins .

Motivação e Introdução aos Fungos

Figura 1: Representação computacional de um micélio fungoso.

Figura 2: Processos de ramificação de fungos. À esquerda a ramificação dicotômica (Dichotomous) e à direita o processo de ramificação lateral .

Fungos estão integrados em grande parte dos ecossistemas do planeta e cumprem importantes funções na manutenção e sobrevivência dos mesmos. De maneira geral, eles produzem enzimas que são responsáveis pela decomposição de matéria orgânica e - portanto - a reciclagem de diversos nutrientes do ambiente ao seu redor . Em muitos casos, fungos formam fusões simbióticas com plantas ou algas e interagem de diferentes maneiras com diferentes organismos vivos. Neste trabalho, todavia, não faremos a análise dessas interações e focaremos no comportamento individual de crescimento de fungos.

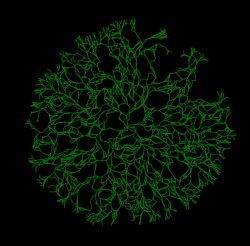
Anatomicamente, fungos são compostos por células que se assemelham a tubos microscópicos, denominadas de hifas. Essas hifas então se ramificam e se fundem umas com as outras em um processo chamado de anastomose, formando uma complexa rede chamada de micélio (figura 1).

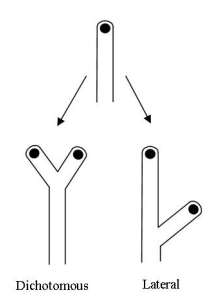
A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de ramificação dicotômica, consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de ramificação lateral, no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na figura 2.

Tendo em vista o objetivo deste trabalho, é importante também entender o porquê e quando as ramificações citadas acimas ocorrem, para que possamos programá-las em nosso modelo computacional. A ramificação, portanto, é atribuída ao acúmulo de partículas de nutrientes e materiais no ambiente, o que estimula a extensão das hifas dos fungos em sua direção. Dessa maneira, o crescimento e desenvolvimento dos fungos são altamente dependentes e influenciados pela disponibilidade de nutrientes e materiais no ambiente ao seu redor. Apesar desse fato, fungos podem continuar se desenvolvendo até em ambientes com poucos nutrientes, devido ao processo de translocação, no qual os nutrientes previamente absorvidos pelo fungo podem ser transportados internamente, bancando o crescimento do mesmo em locais com deficiência de nutrientes.

Mecanismos Gerais dos Modelos

Crescimento e divisão

Tipicamente uma hifa cresce apicalmente em linha reta com pouca variação em sua orientação, enquanto em algumas espécies de fungo as mudanças o ângulo de crescimento seguem uma distribuição normal.

Construção do modelo computacional

Primeiro modelo de Fungo

• Branching na ponta
• Computar só os da ponta
• Crescimento ocorre só com o nutriente que o ponto final está

Segundo modelo de Fungo

• Junção (anastomosis)

Implementação

Crescimento

def crecimento (x,y):

  theta= np.arctan(y/x)

  if (x<0) :
    theta= theta+ math.pi
 
  aleatorio_theta = random.random()* math.pi/4 - math.pi/8 # angulo de -22.5 até 22.5 (45°)
  
  theta=theta+aleatorio_theta

  addx = r * math.cos(theta)
  addy = r * math.sin(theta)
  
  fx = x + addx
  fy = y + addy 

  return (fx,fy)

Divisão

 
def divisao (x,y):

  theta= np.arctan(y/x)

  if (x<0) :
    theta= theta+ math.pi

  angulodivisao= random.random()*math.pi/2 #angulo para divisão de no máximo 90°

  angulo1= theta- angulodivisao/2
  angulo2= theta+ angulodivisao/2

  addx1 = r * math.cos(angulo1)
  addy1 = r * math.sin(angulo1)

  addx2= r * math.cos(angulo2)
  addy2= r * math.sin(angulo2)
  
  Ax = x + addx1
  Ay = y + addy1
  
  Bx = x + addx2
  By= y +addy2

  return (Ax,Ay,Bx,By)

Intersecção de linhas:

[3]

Referências

[1]HOPKINS, Steven. A Hybrid Mathematical Model of Fungal Mycelia: Tropisms, Polarised Growth and Application to Colony Competition, tese de doutorado, 2011.(https://core.ac.uk/download/pdf/6117416.pdf)

[2]DA SILVA, Priscila. Reino Fungi. InfoEscola (2018). Disponível em: https://www.infoescola.com/biologia/reino-fungi. Acesso em: 15 de Maio de 2021.

[3] Line to line intersection. Wikipédia. Disponível em: https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection