Modelo de Bornholdt para simulação de mercados financeiros artificiais

Grupo: Leonardo Barcelos, Luana Bianchi e Rubens Borrasca

Alguns conceitos importantes

Retornos

Quando se trata de sistemas financeiros, os estudos se concentram mais no retorno dos ativos do que no preço em si, pois a série temporal dos retornos tem propriedades estatísticas mais interessantes que a série dos preços.

Sendo P(t) o preço de um ativo financeiro no instante t, e P(t-1) o preço do ativo no instante (t-1), o retorno linear do ativo é:

$r(t)={\frac {P(t)-P(t-1)}{P(t-1)}}$

Reescrevendo esta equação, obtemos que:

$r(t)+1={\frac {P(t)}{P(t-1)}}$

Aplicando a função logarítmica em ambos os lados da equação, e considerando que:

$ln(x+1)\approx x$

obtêm-se o retorno logarítmico, que é mais indicado quando se têm ativos voláteis, que possuem uma variação muito alta:

$r(t)=ln\left({\frac {P(t)}{P(t-1)}}\right)$

Considerando que neste estudo serão comparados retornos de diferentes índices, e também os retornos obtidos através das simulações com o modelo de Bornholdt, é importante normalizar os retornos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{r}_n = \frac{r_n  - \langle r \rangle}{\sigma_r}}

em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_r} é o desvio padrão da serie de retornos e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle r \rangle} a média.

Distribuição dos Retornos

Quando se tem um volume considerável de dados é possível obter a distribuição probabilística deles. Para isso pode-se utilizar a estimação de densidade de Kernel (KDE). Ao observar uma pequena janela de tamanho h em torno de um ponto em análise, pode-se dizer que:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle $P(x-h \leq x \leq x+h ) \approx \frac{1}{N}\sum_n^N W(u) }

sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(u)} uma função kernel e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} uma variável tal que:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \frac{x - x_n}{2h}}

Para este estudo utilizou-se um kernel gaussiano:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}u^2}}

Este método foi aplicado para as séries de retorno para obter a distribuição deles, utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = 0.5 \sigma} .

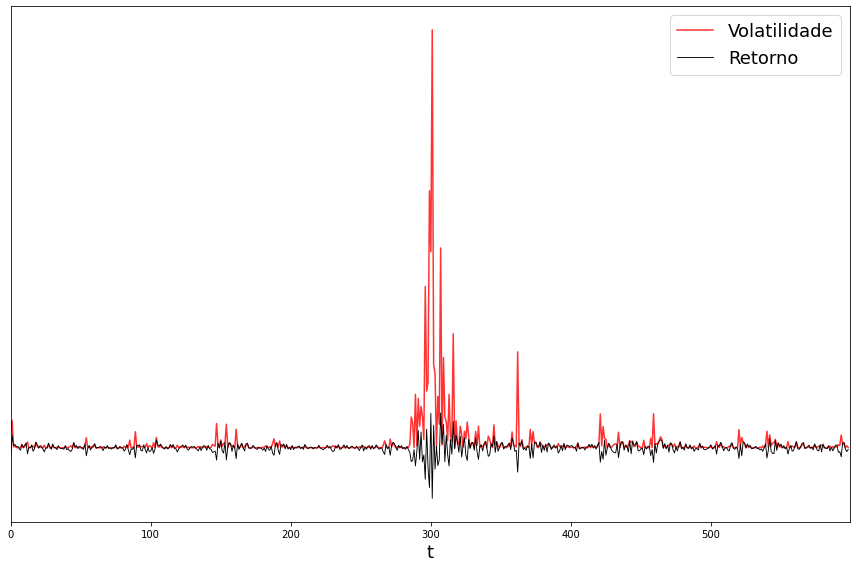
Volatilidade

Uma forma de calcular a volatilidade da série temporal de retornos ao longo do tempo é elevar ao quadrado os valores da série.

O interessante a se verificar é se a volatilidade tem memória, e para isso é preciso verificar se a auto correlação delas apresenta a formação de clusters de volatilidade. Para obter a auto correlação o teorema de Wiener-Khinchin foi utilizado, de forma que:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\tau) =\mathcal{F}\{|S(\omega)|^2\}}

onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\omega)} é a transformada de Fourier do quadrado dos retornos.

Simulações

Variação do tamanho da grade

Em Julia, 8000 passos de MC 16x16: 0.512 s 32x32: 2.332 s 50x50: 10.674 s 100x100: 154.134 s