Difusão ambipolar em plasmas

Equação da difusão ambipolar

Esse trabalho tem como objetivo demonstrar uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma(gás formado de elétrons e íons). A difusão é o modo como um fluido se dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas.

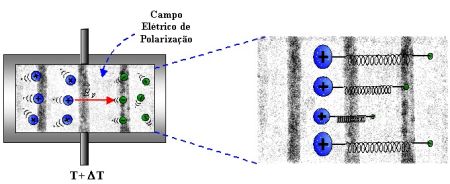
Quando a partição é removida ha uma pertubação instantanea na condição de equilibrio. Os elétrons por ser mais leve difundem-se mais rápido que os íons devido a sua menor massa.

Essa separação de cargas gera um campo elétrico de polarização que aumenta a taxa de difusão dos íons e diminui a dos elétrons até que ocorra um equilíbrio.

Esses movimentos coletivos são caracterizados por uma frequência natural de oscilação(Oscilações de Langmuir).

Como mostrado por Shimony e Cahn, esse problema é descrito por uma equação de onda amortecida para a função de densidade $n({\vec {r}},t)$:

$\nabla ^{2}n({\vec {r}},t)={\frac {1}{u^{2}}}{\frac {\partial ^{2}n({\vec {r}},t)}{\partial t^{2}}}+\alpha {\frac {\partial n({\vec {r}},t)}{\partial t}}\qquad (1)$ ,

onde $u^{2}=\nu _{a}D_{a}$ e $\alpha =1/D_{a}$, sendo $\nu _{a}$ a frequência de colisão ambipolar e $D_{a}$ o coeficiente de difusão ambipolar.

Como tratamos do caso unidimensional, a equação 1 torna-se

${\frac {\partial ^{2}n(x,t)}{\partial x^{2}}}={\frac {1}{u^{2}}}{\frac {\partial ^{2}n(x,t)}{\partial t^{2}}}+\alpha {\frac {\partial n(x,t)}{\partial t}}\qquad (2)$ .

O Método

A resolução numérica do problema foi baseada no artigo de Najafi e Izadi . Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional

${\frac {\partial ^{2}n(x,t)}{\partial t^{2}}}+2h{\frac {\partial n(x,t)}{\partial t}}=c^{2}{\frac {\partial ^{2}n(x,t)}{\partial x^{2}}}\qquad (3)$.

No nosso caso $2h=\alpha u^{2}=\nu _{a}$ e $c^{2}=u^{2}$.

Discretizando as variáveis do problema, temos que

$x_{i}=i\Delta x\qquad i=0,1,2,...,I$ ,

$t_{k}=k\Delta t\qquad k=0,1,2,...,K$.

Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos

${\frac {\partial ^{2}n}{\partial t^{2}}}|_{i}^{k}={\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{2}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})$ ,

${\frac {\partial n}{\partial t}}|_{i}^{k}={\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})$ ,

${\frac {\partial ^{2}n}{\partial x^{2}}}|_{i}^{k}={\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{2}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})$.

Substituindo essas relações na equação 3, obtemos

$\left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]$.

Omitindo todos os temos de ordem $O\{\Delta t^{2},\Delta x^{2}\}$ e isolando $u_{i}^{k_{1}}$, obtemos

$u_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (4)$ ,

sendo $s=(c^{2}\Delta t^{2}/\Delta x^{2})$.

Essa é a equação para resolver o problema para $k\geq 1$, porém o problema envolve uma derivada de segunda ordem no tempo, o que faz com que precisemos saber os dois passos anteriores para calcular o próximo. Então necessitamos ainda de uma maneira de determinar $u_{i}^{1}$ a paritr de $u_{i}^{0}$, para então calcular os demais passos. Para isso assumimos que a função é inicialmente estacionária e fazemos

$n_{t}(x,0)=0\Rightarrow {\frac {n_{i}^{1}-n_{i}^{-1}}{\Delta t}}=0\Rightarrow n_{i}^{1}=n_{i}^{-1}$.

Substituindo na equação 4 para $k=0$ obtemos

$n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (5)$.

Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas (no caso desse trabalho usamos bordas fixas em 0 e também condições periódicas de contorno), podemos calcular a evolução temporal da função de densidade. Esse método é estável para $0\leq s\leq 1$ e seu erro é

$E\{n_{i}^{k}\}=-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}-{\frac {h\Delta t^{2}}{3}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+c^{2}{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O\{\Delta t^{4},\Delta x^{4}\}$.

Resultados e Discussão

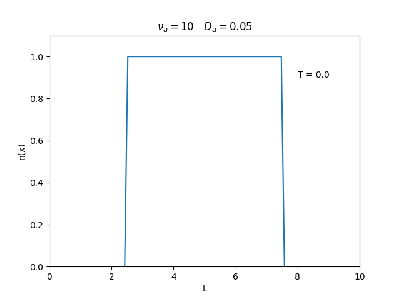
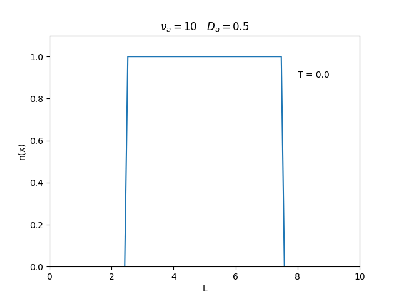
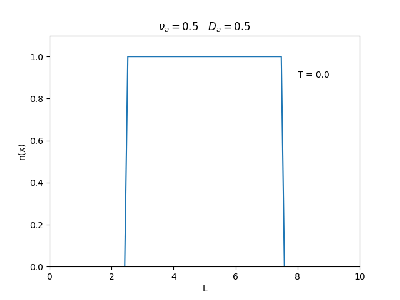
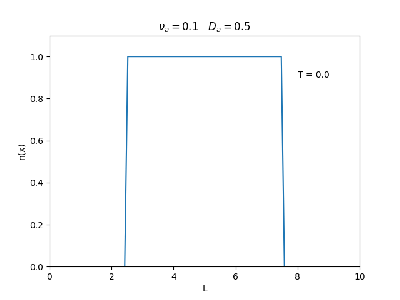
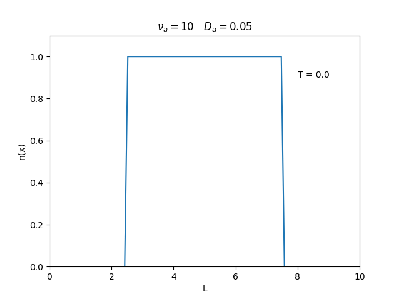
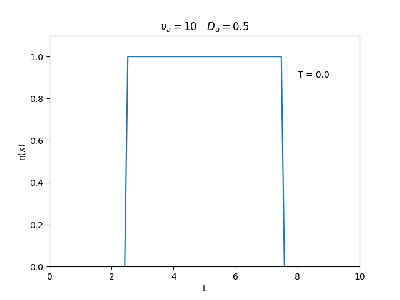
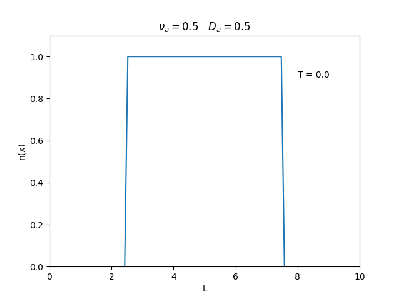
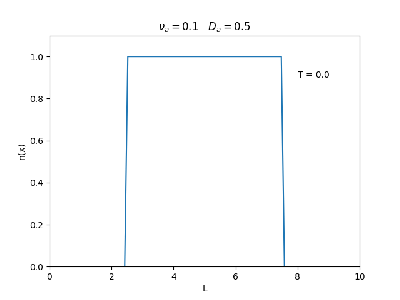
Aplicamos o método descrito acima para simular a evolução da densidade de um plasma se difundindo em um tubo de largura $L=10$. Fizemos o plasma inicialmente concentrado na região central do tubo: $n(x,0)=1$ para $L/4\leq x\leq 3L/4$ e $n(x,0)=0$ para $x$ fora dessa região. Usamos $\Delta x=0.1$ e $\Delta t=0.01$, que resulta em $s=0.01\nu _{a}D_{a}$, e criamos gifs mostrando a evlução temporal da função de densidade para diferentes valores de $\nu _{i}$ e $D_{a}$. Para garantir a estabilidade do método, essas constantes devem ser tais que $0\leq \nu _{i}D_{a}\leq (\Delta x/\Delta t)^{2}$.

Quanto à solução nas bordas, fizemos de duas manerias: A primeira foi com condições de contorno fixas em 0 ($n(0,t)=n(L,t)=0$) e represenda o caso em que as bordas são um sumidouro, como se fosse um tubo aberto. A segunda foi usando condições de contorno periódicas ($n_{I+1}^{k}=n_{0}^{k}$) e representa o caso de um tubo fechado.

Evolução temporal da densidade do plasma para diferentes valores de $\nu _{a}$ e $D_{a}$

Evolução temporal da densidade do plasma para diferentes valores de $\nu _{a}$ e $D_{a}$

Podemos observar que $D_{a}$ é o parâmetro que domina a velocidade com que que a densidade decai, o que é esperado, uma vez que um coeficiente de difusão maior faz o plasma se difundir mais rápido. Já $\nu _{a}$ parece estar ligado à "suavidade" da distribuição, sendo que com frequências baixas começam a aparecer diversos picos de densidade.

Programas Utilizados

Para implementar o método computacionalmente e criar os gifs foram usados códigos em python. O código abaixo é a solução para as bordas fixas em 0:

import numpy as np
import matplotlib.pyplot as plt
import imageio

dt = 0.01
dx = 0.1
L = 10
T = 50

#constantes do plasma
nu_a = 0.1
Da = 0.5

#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2

x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x)))   #matriz com a densidade n(x,t)

#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
    n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+'   $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()

#calculamos o próximo passo considerando dn/dt = 0 inicialmente    
for i in range(1,len(x)-1):
    n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))

#calculamos a posterior evolucao
for k in range(1, len(t)-1):
    for i in range(1,len(x)-1): #isso fixa os contornos em 0
        n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
    if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
       plt.plot(x,n[k])
       plt.title(r'$\nu_a=$'+str(nu_a)+'   $D_a=$'+str(Da))
       plt.xlabel('L')
       plt.ylabel('n(x)')
       plt.xlim([0,L])
       plt.ylim([0,1.1])
       plt.text(8,0.9,'T = '+str(k*dt))
       plt.savefig('n_'+str(int(k*dt))+'.png')
       plt.clf()
    
#criamos gifs usando os plots
images = []
for k in range(T):
    images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'.gif', images, format='GIF', duration=1./10)

O código para as condições de contorno periódicas é levemente diferente, exigindo o acrécimo de duas duas linhas dentro do terceiro loop. Vale notar que aqui não nos preocupamos com o contorno no cáculo de $n_{i}^{1}$ porque a função nos contornos é 0 nos primeiros passos, independente de adotarmos ou não contornos periódicos.

import numpy as np
import matplotlib.pyplot as plt
import imageio

dt = 0.01
dx = 0.1
L = 10
T = 50

#constantes do plasma
nu_a = 0.1
Da = 0.5

#constantes para a eq da onda
c = np.sqrt(nu_a*Da)
h = nu_a/2
s = (c*dt/dx)**2

x = np.linspace(0, L, int(L/dx)) #array com as coordenadas espaciais
t = np.linspace(0, T, int(T/dt)) #array com as coordenadas temporais
n = np.zeros((len(t), len(x)))   #matriz com a densidade n(x,t)

#fazemos o plasma inicialmente concentrado em uma regiao
for i in range(int(len(x)/4),int(3*len(x)/4)):
    n[0,i] = 1
plt.plot(x,n[0]) #plota estado inicial da funcao
plt.title(r'$\nu_a=$'+str(nu_a)+'   $D_a=$'+str(Da))
plt.xlabel('L')
plt.ylabel('n(x)')
plt.ylim([0,1.1])
plt.xlim([0,L])
plt.text(8,0.9,'T = 0.0')
plt.savefig('n_0.png')
plt.clf()

#calculamos o próximo passo considerando dn/dt = 0 inicialmente    
for i in range(1,len(x)-1):
    n[1,i] = 0.5*(2*(1-s)*n[0,i] + s*(n[0,i+1] + n[0,i-1]))

#calculamos a posterior evolucao
for k in range(1, len(t)-1):
    for i in range(1,len(x)-1):
        n[k+1,i] = (1/(1+h*dt))*(2*(1-s)*n[k,i] - (1-h*dt)*n[k-1,i] + s*(n[k,i+1] + n[k,i-1]))
    #condicoes de contorno periodicas
    n[k+1,0] = (1/(1+h*dt))*(2*(1-s)*n[k,0] - (1-h*dt)*n[k-1,0] + s*(n[k,1] + n[k,-1]))
    n[k+1,-1] = (1/(1+h*dt))*(2*(1-s)*n[k,-1] - (1-h*dt)*n[k-1,-1] + s*(n[k,0] + n[k,-2]))
    if k*dt - int(k*dt) == 0: #plota figuras para valores inteiros de t
       plt.plot(x,n[k])
       plt.title(r'$\nu_a=$'+str(nu_a)+'   $D_a=$'+str(Da))
       plt.xlabel('L')
       plt.ylabel('n(x)')
       plt.xlim([0,L])
       plt.ylim([0,1.1])
       plt.text(8,0.9,'T = '+str(k*dt))
       plt.savefig('n_'+str(int(k*dt))+'.png')
       plt.clf()
    
#criamos gifs usando os plots
images = []
for k in range(T):
    images.append(imageio.imread('n_'+str(k)+'.png'))
imageio.mimsave('difusao_ambipolar_'+str(nu_a)+'_'+str(Da)+'PBC.gif', images, format='GIF', duration=1./10)