Equação da difusão ambipolar
A difusão é o modo como um fluido de dilui em um meio. Estudar as equações que governam esse fenômeno e as formas de resolvê-las é de extremo interesse para a física de fluidos e de plasmas, entre outras áreas. Aqui mostramos uma resolução numérica para o caso unidimensional da difusão ambipolar de um plasma (gás formado de elétrons e íons) envolto em um gás neutro, ou seja, o caso de um plasma se espalhando por um tubo.
Diferentemente de um gás de átomos/moléculas neutros(as), os plasmas são menos livres ao se moverem por causa das interações eletromagnéticas envolvidas no movimento das cargas, como a força de Coulomb e a força magnética. Na difusão de plasmas em um gás neutro, os coeficientes de difusão dos elétrons e dos íons são tipicamente dados por
 e
e 
onde  ,
,  ,
,  ,
,  ,
,  e
e  , são as temperaturas, massas e frequências de colisão dos elétrons e íons com os átomos neutros.
Devido à massa do elétron ser muito menor que a massa de um íon,
, são as temperaturas, massas e frequências de colisão dos elétrons e íons com os átomos neutros.
Devido à massa do elétron ser muito menor que a massa de um íon,  é maior que
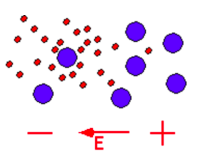
é maior que  , então quando um plasma começa a se difundir, incialmente os elétrons se espalham mais rapidamente que os íons, o que gera um campo elétrico que freia os elétron e acelera os íons. Chamamos esse processo de difusão ambipolar.
, então quando um plasma começa a se difundir, incialmente os elétrons se espalham mais rapidamente que os íons, o que gera um campo elétrico que freia os elétron e acelera os íons. Chamamos esse processo de difusão ambipolar.
 [1]
[1]
Como mostrado por Shimony e Cahn[2], esse problema é descrito por uma equação de onda amortecida

onde  e
e  , sendo
, sendo  a frequência de colisão ambipolar e
a frequência de colisão ambipolar e  o coeficiente de difusão ambipolar, que pode ser escrito como
o coeficiente de difusão ambipolar, que pode ser escrito como  [3].
[3].
Como tratamos do caso unidimensional, a equação 1 torna-se

O Método
A resolução numérica do problema foi baseada no artigo de Najafi e Izadi [4]. Começamos com a forma mais usual de escrever a equação da onda amortecida unidimencional

No nosso caso  e
e  .
.
Discretizando as variáveis do problema, temos que


Substituindo as derivadas que aparecem na equação por diferenças finitas, obtemos



Substituindo essas relações na equação 3, obtemos
![{\displaystyle \left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93087b881e6f091b23454095fc236ac34ab6fa3)
Omitindo todos os temos de ordem  e isolando
e isolando  , obtemos
, obtemos
![{\displaystyle u_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa639b148175f1c3f4f9ce5640f6087e53b54729)
sendo  .
.
Essa é a equação para resolver o problema para  , mas nessecitamos ainda de uma maneira de determinar
, mas nessecitamos ainda de uma maneira de determinar  a paritr de
a paritr de  . Para isso assumimos que a função é inicialmente estacionária e fazemos
. Para isso assumimos que a função é inicialmente estacionária e fazemos

Substituindo na equação 4 para  obtemos
obtemos
![{\displaystyle n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/296c55fd74de89c822e92dce454986bb832cb203)
Com as equações 4 e 5, e tomando as devidas condições de contorno nas bordas, podemos calcular a evolução temporal da função de densidade. Esse método é estável para  e seu erro é
e seu erro é

Resultados e Discussão
Programas Utilizados
Referências


























![{\displaystyle \left[{\frac {n_{i}^{k+1}-2n_{i}^{k}+n_{i}^{k-1}}{\Delta t^{2}}}-{\frac {\Delta t^{2}}{12}}{\frac {\partial ^{4}n}{\partial t^{4}}}|_{i}^{k}+O(\Delta t^{4})\right]+2h\left[{\frac {n_{i}^{k+1}-n_{i}^{k-1}}{2\Delta t}}-{\frac {\Delta t^{2}}{6}}{\frac {\partial ^{3}n}{\partial t^{3}}}|_{i}^{k}+O(\Delta t^{4})\right]=c^{2}\left[{\frac {n_{i+1}^{k}-2n_{i}^{k}+n_{i-1}^{k}}{\Delta x^{2}}}-{\frac {\Delta x^{2}}{12}}{\frac {\partial ^{4}n}{\partial x^{4}}}|_{i}^{k}+O(\Delta x^{4})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93087b881e6f091b23454095fc236ac34ab6fa3)


![{\displaystyle u_{i}^{k+1}={\frac {1}{1+h\Delta t}}[2(1-s)n_{i}^{k}-(1-h\Delta t)n_{i}^{k-1}+s(n_{i+1}^{k}+n_{i-1}^{k})]\qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa639b148175f1c3f4f9ce5640f6087e53b54729)






![{\displaystyle n_{i}^{1}={\frac {1}{2}}[2(1-s)n_{i}^{0}+s(n_{i+1}^{0}+n_{i-1}^{0})]\qquad (5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/296c55fd74de89c822e92dce454986bb832cb203)

