Equações de Laplace e Poisson

Grupo: Augusto M Giani e Henrique Padovani

O objetivo deste trabalho é implementar os métodos de Relaxação, Gauss-Seidel e SOR (Simultaneous OverRelaxation) em problemas de eletroestática, resolvidos pelas equações de Laplace e Poisson. Também temos como objetivo comparar seus resultados: erro entre os métodos e a solução analítica, tempo para estabilização das soluções.

Problema físico envolvendo as Equações de Laplace e Poisson

A Equação de Laplace descreve o Potencial Elétrico ($\Phi$) de uma determinada região num espaço que não possui nenhuma densidade de carga elétrica (corpo carregado):

$\nabla ^{2}\Phi =0$

ou na sua versão em 2 dimensões: ${\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial y^{2}}}=0$

Quando neste determinado espaço, delimitado pelas condições de contorno, existe uma densidade de carga, o campo $\Phi$ já não se iguala mais à zero, mas sim à densidade de cargas dentro daquela região, sendo descrito agora pela Equação de Poisson:

$\nabla ^{2}\Phi ={\frac {-\rho (x,y)}{\epsilon _{0}}}$

ou na sua versão em 2 dimensões: ${\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial y^{2}}}={\frac {-\rho (x,y)}{\epsilon _{0}}}$

Método de Relaxação

Como podemos ver ambas as equações não dependem do tempo, porém podemos usar um truque para resolver estas equações aplicando o método **FTCS** (Forward Time Central Space) em uma equação parecida, e fazer a evoluçao temporal durar tempo sufiente para a solução convergir ($t\rightarrow \infty$). Esta operação é chamada de Método de Relaxação.

O que usamos para convergir à solução da Equação de Laplace foi uma equação de difusão genérica:

${\frac {\partial f}{dt}}=D\cdot \left({\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}}\right)$

Fazendo $t\rightarrow \infty$, para a equação de difusão temos a intuição que dada condição inicial estacionária, a solução não diverge e "relaxa" para uma função que não depende mais do tempo:

$\lim _{t\rightarrow \infty }f(x,y,t)=f(x,y)$

Com isso: ${\frac {\partial f}{\partial t}}=0$, e chegando assim à Equação de Laplace e possibilitando chegar na discretização da Equação de Poisson. Então basicamente utiliza-se da mesma discretização de uma equação de difusão, porém a evolução temporal só serve para convergirmos à solução da Equação de Laplace com as condições iniciais que propomos. Os métodos de Jacobi, Gauss-Seidel e SOR são considerados Métodos de Relaxação.

Discretizações

Método de Jacobi "FTCS"

Equação de Laplace $\nabla ^{2}\Phi =0$

Para equação de Laplace partimos de:

${\frac {\partial \Phi }{\partial t}}=\mu \left({\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial y^{2}}}\right)$

Discretizando, primeiro chegamos que:

$\Phi _{i,j}^{n+1}=\Phi _{i,j}^{n}+\mu \Delta t\left({\frac {\Phi _{i-1,j}^{n}-2\Phi _{i,j}^{n}+\Phi _{i+1,j}^{n}}{(\Delta x)^{2}}}+{\frac {\Phi _{i,j-1}^{n}-2\Phi _{i,j}^{n}+\Phi _{i,j+1}^{n}}{(\Delta y)^{2}}}\right)$

Seguindo mesmo procedimento do método de FTCS, temos a mesma condição de estabilidade:

${\frac {\mu \Delta t}{(\Delta x)^{2}}}+{\frac {\mu \Delta t}{(\Delta y)^{2}}}\leq {\frac {1}{2}}$

No nosso algoritmo ultizamos $\Delta x=\Delta y$ então obtivemos a condição de estabilidade:

${\frac {\mu \Delta t}{(\Delta x)^{2}}}\leq {\frac {1}{4}}$

Para o algoritmo de Jacobi (Relaxação) escolhemos o valor de ${\frac {1}{4}}$ e com isso resulta na equação final:

$\color {MidnightBlue}\Phi _{i,j}^{n+1}={\frac {1}{4}}\left(\Phi _{i-1,j}^{n}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n}+\Phi _{i,j+1}^{n}\right)$

onde n representa o passo no tempo, i representa o passo em X e j representa o passo em Y. A constante $\mu$ somente representava uma similaridade com a equação de difusão para demonstrar que este valor não interfere na equação final, ele sequer aparece (portanto podemos desconsiderá-lo, como faremos na equação de Poisson).

Equação de Poisson $\nabla ^{2}\Phi ={\frac {-\rho (x,y)}{\epsilon _{0}}}$

Partindo de:

${\frac {\partial \Phi }{\partial t}}={\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial y^{2}}}+{\frac {\rho (x,y)}{\epsilon _{0}}}$

chegamos em:

$\Phi _{i,j}^{n+1}=\Phi _{i,j}^{n}+\Delta t\left({\frac {\Phi _{i-1,j}^{n}-2\Phi _{i,j}^{n}+\Phi _{i+1,j}^{n}}{(\Delta x)^{2}}}+{\frac {\Phi _{i,j-1}^{n}-2\Phi _{i,j}^{n}+\Phi _{i,j+1}^{n}}{(\Delta y)^{2}}}\right)+{\frac {\Delta t\rho _{i,j}}{\epsilon _{0}}}$

Para nosso problema $\Delta x=\Delta y$, então multiplicando os dois lados por ${\frac {\Delta x^{2}}{\Delta t}}$, chegamos em:

$\Phi _{i,j}^{n+1}{\frac {\Delta x^{2}}{\Delta t}}={\frac {\Delta x^{2}}{\Delta t}}\Phi _{i,j}^{n}-4\Phi _{i,j}^{n}+\Phi _{i-1,j}^{n}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n}+\Phi _{i,j+1}^{n}+{\frac {\Delta x^{2}\rho _{i,j}}{\epsilon _{0}}}$

E finalmente, aplicando a condição de estabilidade ${\frac {\Delta t}{\Delta x^{2}}}={\frac {1}{4}}$ e cancelando os termos $\Phi _{i,j}^{n}$:

$\color {MidnightBlue}\Phi _{i,j}^{n+1}={\frac {1}{4}}\left(\Phi _{i-1,j}^{n}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n}+\Phi _{i,j+1}^{n}+{\frac {\Delta x^{2}\rho _{i,j}}{\epsilon _{0}}}\right)$

Método de Gauss-Seidel

Como pode-se notar, o termo que distingue a Equação de Laplace para a Equação de Poisson é apenas o termo que soma $\left({\frac {1}{4}}{\frac {\Delta x^{2}\rho _{i,j}}{\epsilon _{0}}}\right)$ ao lado direito da equação. Para demonstrar as próximas discretizações, as deduções foram deixadas de lado pelo fato de que são irrelevantes, tendo entendido de onde vem as equações.

O Método de Gauss-Seidel adianta (no tempo) a chegada da solução estacionária, utilizando termos que já foram calculados num passo anterior de tempo para calcular o ponto atual, respectivamente para equação de Laplace e Poisson, utilizamos na nossa implementação:

$\color {MidnightBlue}\Phi _{i,j}^{n+1}={\frac {1}{4}}\left(\Phi _{i-1,j}^{n+1}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n+1}+\Phi _{i,j+1}^{n}\right)$

e

$\color {MidnightBlue}\Phi _{i,j}^{n+1}={\frac {1}{4}}\left(\Phi _{i-1,j}^{n+1}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n+1}+\Phi _{i,j+1}^{n}+{\frac {\Delta x^{2}\rho _{i,j}}{\epsilon _{0}}}\right)$

Método SOR, Simultaneous Overrelaxation

Como pode-se notar nas equações (é mais intuitivo na forma discretizada da Equação de Laplace), a atualização de um ponto $\Phi _{i,j}^{n+1}$ é feita através de uma espécie de "média" dos pontos, no tempo anterior, ao seu arredor (o ponto acima, à direita, à esquerda e abaixo na matriz dos $\Phi _{i,j}$). O método introduz nesse cálculo de "média" (ainda no método de Gauss-Seidel), pesos para a contribuição dos pontos da vizinhança e também um peso para o próprio ponto no tempo anterior. Respectivamente para a Equação de Laplace e para Poisson:

$\color {MidnightBlue}\Phi _{i,j}^{n+1}=\left(1-\omega \right)\Phi _{i,j}^{n}+{\frac {\omega }{4}}\left(\Phi _{i-1,j}^{n+1}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n+1}+\Phi _{i,j+1}^{n}\right)$

e

$\color {MidnightBlue}\Phi _{i,j}^{n+1}=\left(1-\omega \right)\Phi _{i,j}^{n}{\frac {\omega }{4}}\left(\Phi _{i-1,j}^{n+1}+\Phi _{i+1,j}^{n}+\Phi _{i,j-1}^{n+1}+\Phi _{i,j+1}^{n}+{\frac {\Delta x^{2}\rho _{i,j}}{\epsilon _{0}}}\right)$

As equações em Azul descritas acima foram as que implementamos em nossos códigos.

Problemas propostos

Problema 1

Equação de Laplace aplicada a um plano $L\times L$ com uma das quatro "bordas" carregada. Consideramos as dimensões de $L_{x}$ e $L_{y}$ como $L$ (um plano quadrado) para facilitar os cálculos.

Condições iniciais e de contorno:

${\begin{cases}\Phi (x=0,y)=\Phi _{0}=1\\\Phi (x=L,y)=\Phi (x,y=0)=\Phi (x,y=L)=0\\\end{cases}}$

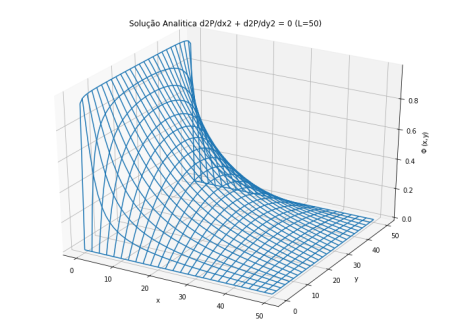
Para a solução analítica do problema temos que:

$\Phi (x,y)=\Phi _{0}\sum _{i=1,2,3,...}^{\infty }{\frac {4}{\pi n}}\left({\frac {n\pi x}{L}}\right){\frac {\sinh(n\pi y/L)}{\sinh(n\pi )}}$

Solução analítica do problema 1

Implementação

Implementamos as simulações em Python3, no ambiente Colab da Google. Junto com as soluções numéricas também implementamos a solução analítica de um problema para compararmos com a solução numérica

Os códigos se encontram no final desta Wiki, mas uma observação geral é que além de utilizarmos as equações destacadas em Azul para implementar as soluções, é importante lembrar que o resultado final só é atingido quando iteramos as soluções no "tempo", então é preciso iterar os elementos da matriz no espaço, mas também fazer ela evoluir com o tempo, exemplo para o algoritmo de Jacobi, Equação de Laplace:

### Exemplo da evolução temporal no método de relaxação ###
# P é a matriz do potencial no tempo n
# Q é a matriz do potencial no tempo n+1

while t < tmax: # Loop temporal
  
  for i in range(1,L+1):  # Loop em x
    for j in range(1,L+1): # Loop em y
      Q[i][j] = (P[i+1][j] + P[i-1][j] + P[i][j+1] + P[i][j-1])/4 
  
  P = Q.copy()
  t = t + td

plt.plot(x,y,P)

Lembrando que estamos resolvendo o problema em 2D, por isso P e Q são matrizes, onde cada elemento representa um ponto no plano. Como pode-se ver, somente é plotado um gráfico, ou somente se é considerado como resultado final o estado final do vetor P, depois que ele sai do loop while. Esta lógica foi usada para todos os métodos que aplicamos.

Resultados

FTCS, Equação de Laplace

Obtivemos a seguinte solução pelo método explícito:

[Gráfico solução numérica]

Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:

[Colocar 2 gráficos de diferenças entre o passo n+1 e passo n]

E o gráfico de erro em relação à solução analítica:

[colocar gráfico de Erro comparando com a solução analítica]

Gauss-Seidel, Equação de Laplace

Obtivemos a seguinte solução pelo método de Gauss-Seidel:

[Gráfico solução numérica]

Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:

[Colocar 2 gráficos de diferenças entre o passo n+1 e passo n]

E o gráfico de erro em relação à solução analítica:

[colocar gráfico de Erro comparando com a solução analítica]

Importante ressaltar que para uma quantidade menor de iterações no tempo, obtivemos erros menores, comparando com o método explícito, o que mostra a eficácia do método.

SOR, Equação de Laplace

Obtivemos a seguinte solução aprimorando o método de Gauss-Seidel para Simultaneous OverRelaxation:

[Gráfico solução numérica]

Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:

[Colocar 2 gráficos de diferenças entre o passo n+1 e passo n]

E o gráfico de erro em relação à solução analítica:

[colocar gráfico de Erro comparando com a solução analítica]

Importante ressaltar que este método além de convergir mais rápido para uma solução, ele apresenta menos erro com menos iterações do que o método de Gauss-Seidel, isso se deve ao fato que ele leva em consideração o seu mesmo ponto no passo anterior para atualizá-lo no próximo passo, deixando o método mais preciso.

Métodos com a Equação de Poisson

Não sei o que escrever aqui kkk

[]

Discussão

[Colocar gráficos único com as 3 curvas dos 3 métodos.]