Grupo - Equações de Schrödinger não-lineares acopladas

Enrique Augusto Tiran Calderoli (00276132)

Bósons são partículas de spin inteiro e possuem funções de onda simétricas. Tais partículas obedecem às estatísticas de Bose-Einstein, de forma que a existência de múltiplas partículas (deste tipo) indistinguíveis em um mesmo estado quântico é possível.

Condensado de Bose-Einstein e Equação de Schrödinger Não-Linear

Para temperaturas muito próximas de zero absoluto, uma parte considerável de um sistema de muitos bósons vai se encontrar no seu estado de menor energia, ou seja, no mesmo estado de menor energia. A acumulação de bósons neste estado fundamental é chamada de condensado de Bose-Einstein. Um dos fatos mais interessantes do ponto de vista experimental deste tipo de condensado é que fenômenos quânticos se tornam visíveis macroscopicamente. No caso de temperaturas ultrafrias (em concordância com a maioria dos experimentos envolvendo átomos alcalinos), a dinâmica do estado de partículas condensadas pode ser modelada por meio da equação de Schrödinger não-linear. Neste caso o condensado é descrito por uma única função de onda $\psi ({\vec {r}})$, e $\vert \psi ({\vec {r}})\vert ^{2}$ é interpretado como a densidade de partícula. Consequentemente o número total de átomos é dado por:

$N=\int d{\vec {r}}\vert \psi ({\vec {r}})\vert ^{2}$

A energia associada a este estado $\psi ({\vec {r}})$ do condensado para bósons no estado fundamental é, de acordo com a teoria de campo médio, igual a

$E=\int d{\vec {r}}\left({\frac {\hbar ^{2}}{2m}}\vert \nabla \psi ({\vec {r}})\vert ^{2}+V({\vec {r}})\vert \psi ({\vec {r}})\vert ^{2}+{\frac {1}{2}}U_{o}\vert \psi ({\vec {r}})\vert ^{4}\right)$

A minimização desta energia no que diz respeito a variações infinitesimais de $\psi ({\vec {r}})$, com um número total de átomos constante, permite obter a seguinte equação de Schrödinger não-linear

$i\hbar {\frac {\partial \psi ({\vec {r}})}{\partial t}}=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi ({\vec {r}})+V({\vec {r}})\psi ({\vec {r}})+U_{o}\vert \psi ({\vec {r}})\vert ^{2}\psi ({\vec {r}})$

Método Numérico

A equação de Schrödinger dependente do tempo pode ser escrita em notação de operadores como

$i\hbar {\frac {\partial \psi }{\partial t}}=H\psi$

onde H representa o operador Hamiltoniano do sistema. Como H é um operador linear, uma possível discretização da equação acima é dada por

$i\hbar {\frac {\psi _{j}^{n+1}-\psi _{j}^{n}}{\Delta t}}=\sum _{k=0}^{N-1}H_{jk}\psi _{k}^{n}$

Esta forma é conhecida como uma forma explícita no tempo, uma vez que o valor futuro de $\psi$ depende exclusivamente do valor atual de $\psi$. Em notação matricial, o desenvolvimento algébrico da expressão acima fornece

$\Psi ^{n+1}=\left(\mathbf {I} -{\frac {i\Delta t}{\hbar }}\mathbf {H} \right)\Psi ^{n}$

onde $\Psi ^{n}$ é o vetor coluna com os valores de $\psi$ no tempo n, e $\mathbf {I}$ é a matriz identidade. Outra forma possível de discretização é a discretização implícita no tempo, dada por

$i\hbar {\frac {\psi _{j}^{n+1}-\psi _{j}^{n}}{\Delta t}}=\sum _{k=0}^{N-1}H_{jk}\psi _{k}^{n+1}$

em que o valor futuro de $\psi$ depende tanto dos valores atual e futuro de $\psi$. É possível mostrar que a forma matricial que corresponde à equação acima é dada por

$\Psi ^{n+!}=\left(\mathbf {I} +{\frac {i\Delta t}{\hbar }}\mathbf {H} \right)^{-1}\Psi ^{n}$

O método de Crank-Nicolson, por sua vez, consiste em tomar a média dos esquemas explícito e implícito, de forma que

$i\hbar {\frac {\psi _{j}^{n+1}-\psi _{j}^{n}}{\Delta t}}={\frac {1}{2}}\sum _{k=0}^{N-1}H_{jk}(\psi _{k}^{n}+\psi _{k}^{n+1})$

Tal método, além de possuir alta acurácia, é incondicionalmente estável na integração de muitas equações diferenciais parciais. Tomando a versão matricial da equação de Schrödinger discretizada por Crank-Nicolson, obtém-se

$\Psi ^{n+1}=\Psi ^{n}-{\frac {i\Delta t}{2\hbar }}\mathbf {H} (\Psi ^{n}+\Psi ^{n+!})$

ou ainda, por manipulação algébrica,

$\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)\Psi ^{n+1}=\left(\mathbf {I} -{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)\Psi ^{n}$

Isolando o termo $\Psi ^{n+1}$ na expressão acima, encontra-se

$\Psi ^{n+1}=\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)^{-1}\left(\mathbf {I} -{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)\Psi ^{n}$

Implementação e Código

A integração da equação de Schrödinger pelo método de Crank-Nicolson

$\Psi ^{n}=\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)^{-1}\left(\mathbf {I} -{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)\Psi ^{n}$

pode ser reescrita na seguinte forma

$\Psi ^{n+!}=\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)^{-1}\left[2\mathbf {I} -\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)\right]\Psi ^{n}=\left[2\left(\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right)^{-1}-\mathbf {I} \right]\Psi ^{n}$

Definindo $\mathbf {Q} ={\frac {1}{2}}\left[\mathbf {I} +{\frac {i\Delta t}{2\hbar }}\mathbf {H} \right]$, a equação acima pode ser expressa como

$\Psi ^{n}=(\mathbf {Q} ^{-1}-\mathbf {I} )\Psi ^{n}=\mathbf {Q} ^{-1}\Psi ^{n}-\Psi ^{n}$

Portanto, a evolução dinâmica do sistema pode ser avaliada separando o processo em duas partes. Primeiramente, o sistema linear

$\mathbf {Q} {\boldsymbol {\chi }}=\Psi ^{n}$

é resolvido para o vetor ${\boldsymbol {\chi }}$ e, em sequência, os valores da função de onda são atualizados de acordo com

$\Psi ^{n+1}={\boldsymbol {\chi }}-\Psi ^{n}$

Uma matriz tridiagonal possui a seguinte forma

$\mathbf {A} ={\begin{bmatrix}\beta _{0}&\gamma _{0}&0&\cdots &0\\\alpha _{0}&\beta _{1}&\gamma _{1}&\cdots &0\\0&\alpha _{1}&\beta _{2}&\cdots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\0&0&0&\cdots &\beta _{N-1}\end{bmatrix}}$

ou seja, apenas os termos da diagonal principal e os termos imediatamente acima ou abaixo são não-nulos. Ela pode ser armazenada de forma mais compacta no formato

$A_{c}={\begin{bmatrix}*&\beta _{0}&\gamma _{0}\\\alpha _{0}&\beta _{1}&\gamma _{1}\\\alpha _{1}&\beta _{2}&\gamma _{2}\\\vdots &\vdots &\vdots \\\alpha _{N-2}&\beta _{N-1}&*\end{bmatrix}}$

onde os elementos denotados por um asterisco não são utilizados.

Consequentemente, o sistema linear $\mathbf {Ax} =\mathbf {b}$ pode ser resolvido pelo método de eliminação Gaussiana, também conhecido como algoritmo de Thomas neste caso. O procedimento é dividido em duas partes: por primeiro, a eliminação progressiva é realizada, que consiste em determinar equações lineares equivalentes que independam de $\alpha _{i}$. Neste passo, as equações recursivas para os novos elementos da diagonal principal $\beta _{i}$ e do vetor $\mathbf {b}$ são

$\beta '_{i}=\beta _{i}-{\frac {\alpha _{i-1}}{\beta '_{i-1}}}\gamma _{i-1},\;\;\;\;\;i=1,...,N-1$

e

$b'_{i}=b_{i}-{\frac {\alpha _{i-1}}{\beta '_{i-1}}}b'_{i-1},\;\;\;\;\;i=1,...,N-1$

com $\beta '_{0}=\beta _{0}$ e $b'_{0}=b_{0}$. Na etapa seguinte, em que ocorre a chamada substituição regressiva, a última equação é resolvida para obter $x_{N-1}=b'_{N-1}/\beta '_{N-1}$, e este resultado é inserido na equação anterior, gerando uma relação recursiva da forma

$x_{i}={\frac {b'_{i}-\gamma _{i}x_{i+1}}{\beta '_{i}}},\;\;\;\;\;i=N-2,...,0$

Como a matriz $\mathbf {Q}$ é tridiagonal, o sistema linear $\mathbf {Q} {\boldsymbol {\chi }}=\Psi ^{n}$ pode ser resolvido com o uso do algoritmo de Thomas para obter ${\boldsymbol {\chi }}$ e, em sequência, ${\boldsymbol {\chi }}$ é utilizado para obter $\Psi ^{n+1}$.

O código abaixo foi implementado para integrar numericamente duas equações de Schrödinger não-lineares acopladas, que foram discretizadas sobre uma rede unidimensional da seguinte forma

$i\hbar {\frac {\partial \psi _{i}}{\partial t}}=-\omega (\psi _{i-1}+\psi _{i+1})+V_{i}\psi _{i}+U_{1}\vert \psi _{i}\vert ^{2}\psi _{i}+U_{2}\vert \phi _{i}\vert ^{2}\psi$

e

$i\hbar {\frac {\partial \phi _{i}}{\partial t}}=-\omega (\phi _{i-1}+\phi _{i+1})+V_{i}\phi _{i}+U_{1}\vert \phi _{i}\vert ^{2}\phi _{i}+U_{2}\vert \psi _{i}\vert ^{2}\phi _{i}$

e que representam a evolução dinâmica de dois condensados de Bose-Einstein nesta mesma rede. O último termo de ambas as equações denota o acoplamento do sistema.

Para esta integração numérica, foram utilizados $N=301$ sítios, para um período total de 50 “segundos” e um passo de tempo de $\Delta t=0,001$ “segundos”, onde as unidades de tempo possuem aspas pois são adimensionais ($\tau =\omega t/\hbar$).

Código em Fortran para a integração numérica:

Equações de Schrödinger não-lineares acopladas

Aplicações

Abaixo é possível visualizar a evolução dinâmica de uma das funções de onda (o comportamento da outra é simétrico) nos sítios centrais da rede unidimensional em questão para dois conjuntos de parâmetros físicos. No primeiro caso, tanto o campo elétrico aplicado F como o segundo potencial $U_{2}$, ao passo que o primeiro potencial vale $U_{1}=0.1$. No segundo caso o campo elétrico vale $F=4$ e ambos os potenciais são iguais a $U_{1}=U_{2}=3$. O eixo vertical representa a intensidade da função de onda, que tem condição inicial unitária no sítio central. Um dos eixos horizontais representa os sítios ao redor do sítio central e o outro eixo representa a evolução temporal, de 0 a 30. Nota-se que no primeiro caso a função de onda apresenta grande dispersão, se difundindo pela rede, ao passo que no segundo caso ela permanece muito mais localizada ao redor do sítio inicial (Observação: o gráfico apresentado na segunda imagem foi girado em relação à primeira imagem pois a angulação adotada permite uma melhor visualização das propriedades de localização da função de onda nos sítios centrais).

Gráfico 1: Evolução da função de onda na rede para $F=0$, $U_{1}=0.1$ e $U_{2}=0$.

Gráfico 2: Evolução da função de onda na rede para $F=4$, $U_{1}=3$ e $U_{2}=3$.

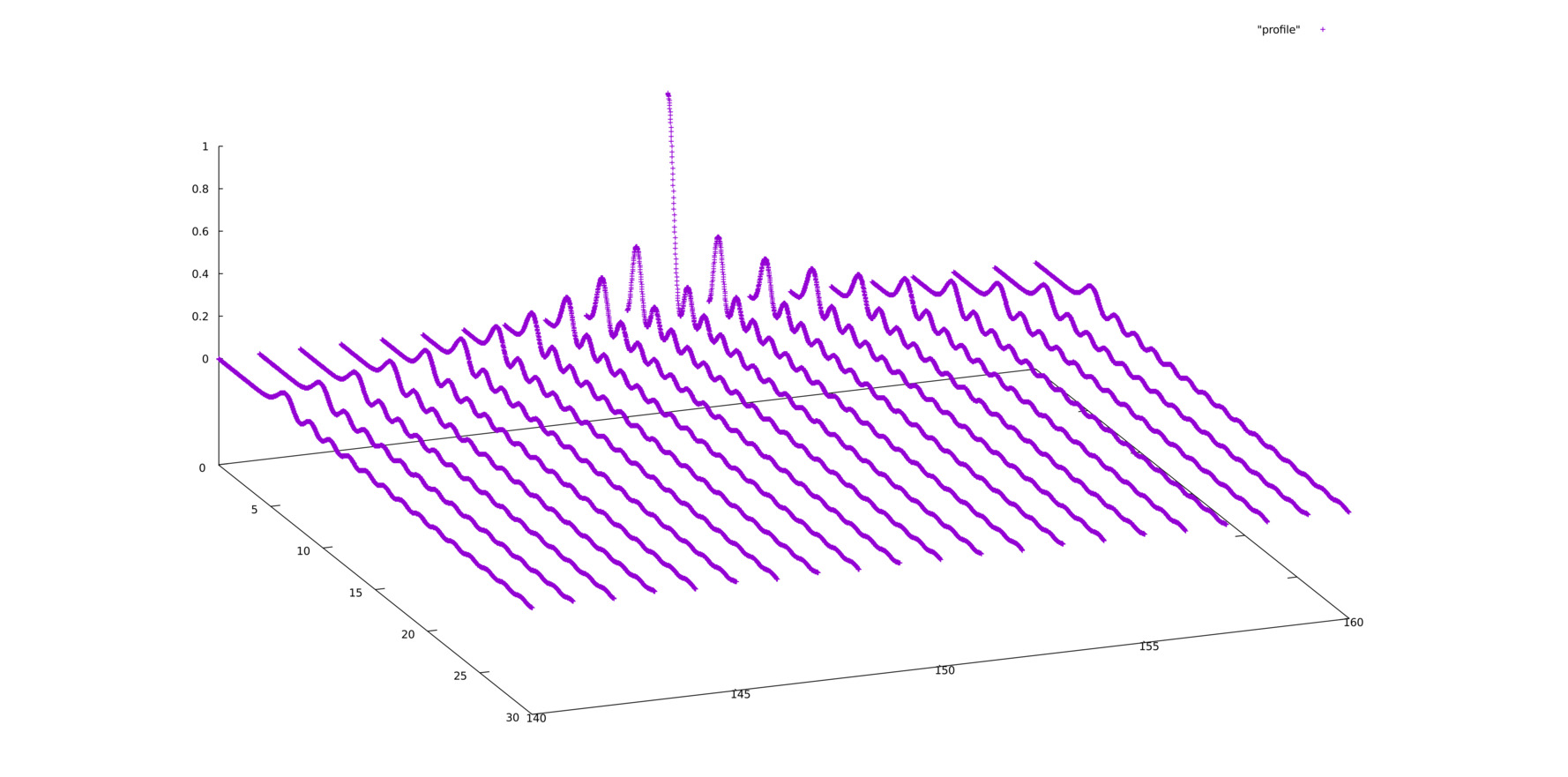
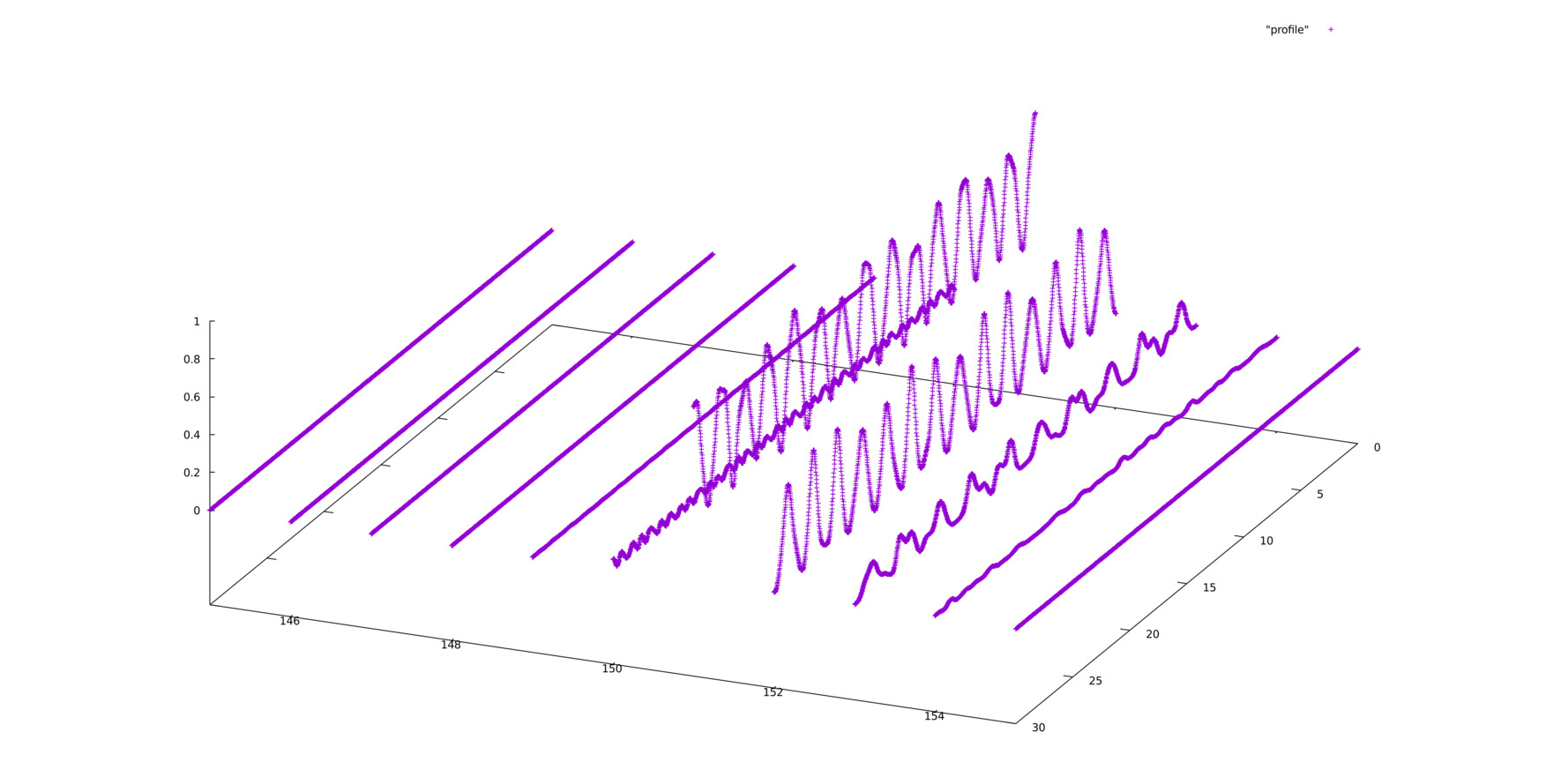
As oscilações de Bloch são oscilações características de uma partícula em um potencial confinante periódico e sujeita a uma força constante. Partindo da equação de movimento unidimensional para um elétron, por exemplo, submetido a um campo elétrico constante F, e usando as relações de física de estado sólido, é possível mostrar que a posição do elétron é uma função oscilatória. O período destas oscilações é dado por

$T_{B}={\frac {2\pi \hbar }{dF}}$

onde d representa a distância entre os poços de potencial confinante periódicos.

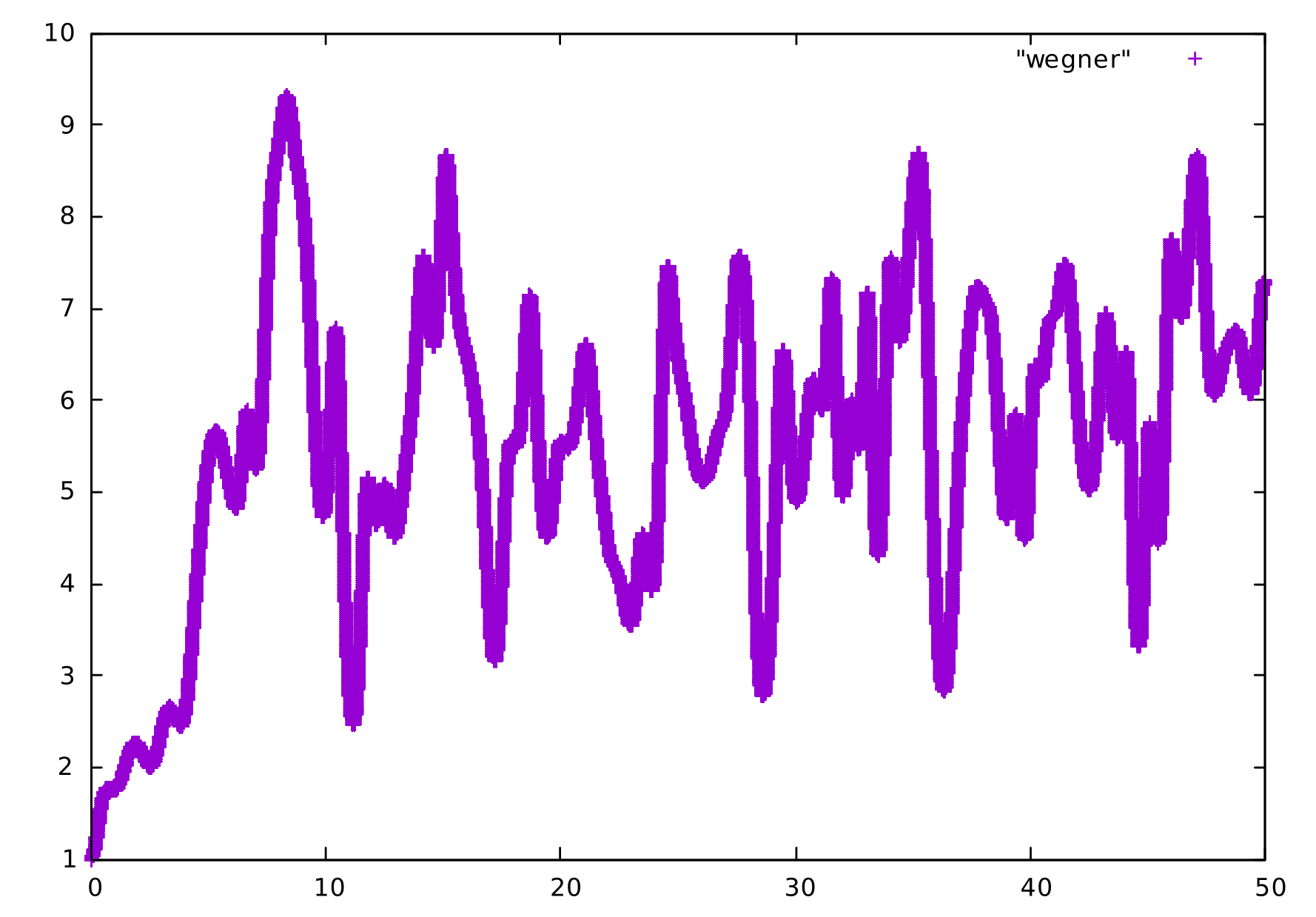
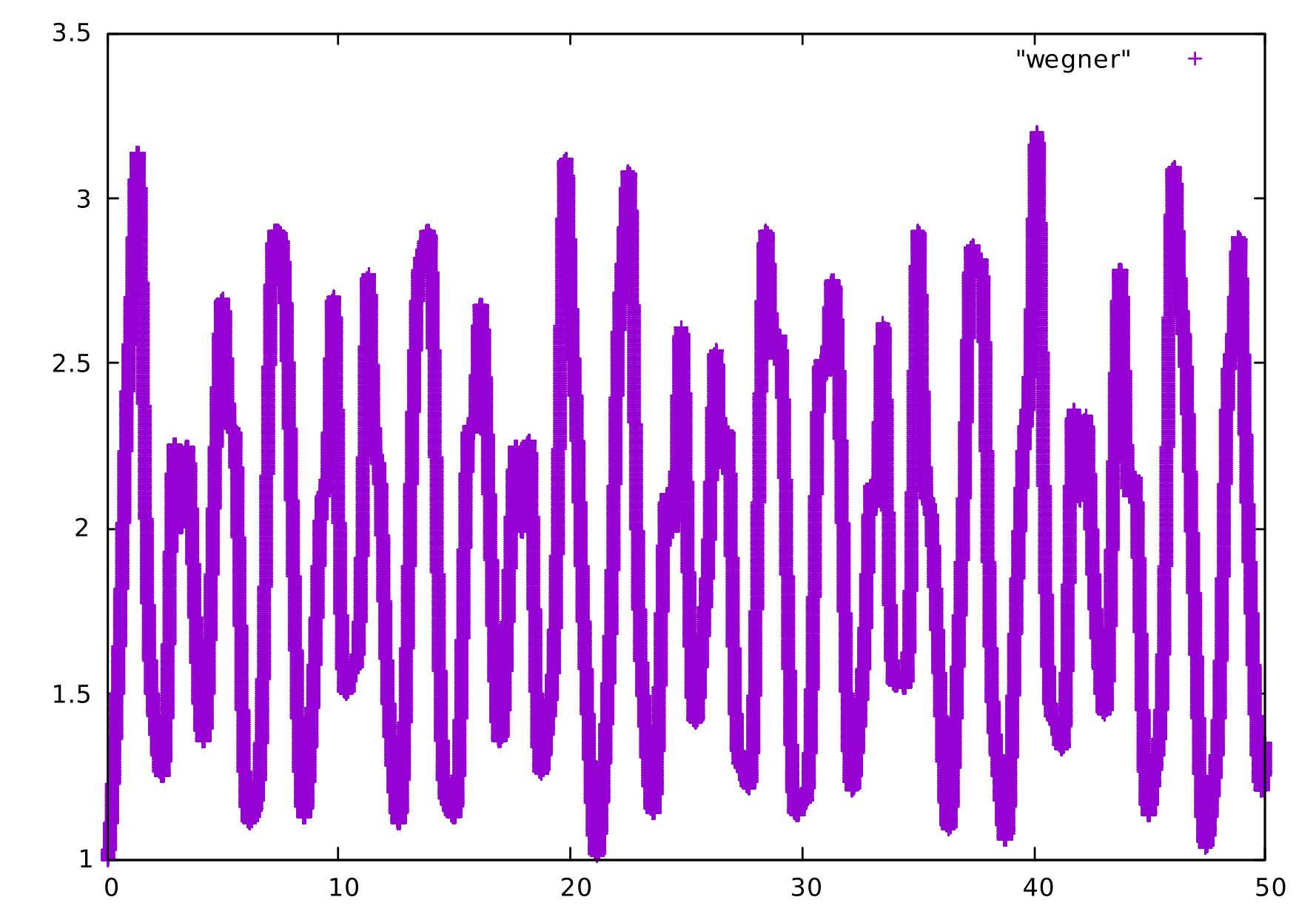
Uma das variáveis que podem ser estudadas com a implementação numérica mostrada acima é a função de participação de Wegner. Ela é definida por

$W(t)=\left[\sum _{i=1}^{N}\vert \psi _{i}(t)\vert ^{4}\right]^{-1}$

e seu valor cresce com o espalhamento espacial da probabilidade de ocupação de um sítio. Nas duas imagens abaixo, a função de Wegner é plotada como função do tempo para os casos de campo $F=1$, $U_{1}=3$ e $U_{2}=3$ e de campo $F=4$, $U_{1}=3$ e $U_{2}=3$. É possível notar que o aumento da intensidade do campo aplicado resulta em uma frequência maior das oscilações de Bloch, em concordância com a previsão teórica.

Gráfico 3: Função de Wegner como função do tempo para $F=1$, $U_{1}=3$ e $U_{2}=3$.

Gráfico 4: Função de Wegner como função do tempo para $F=4$, $U_{1}=3$ e $U_{2}=3$.

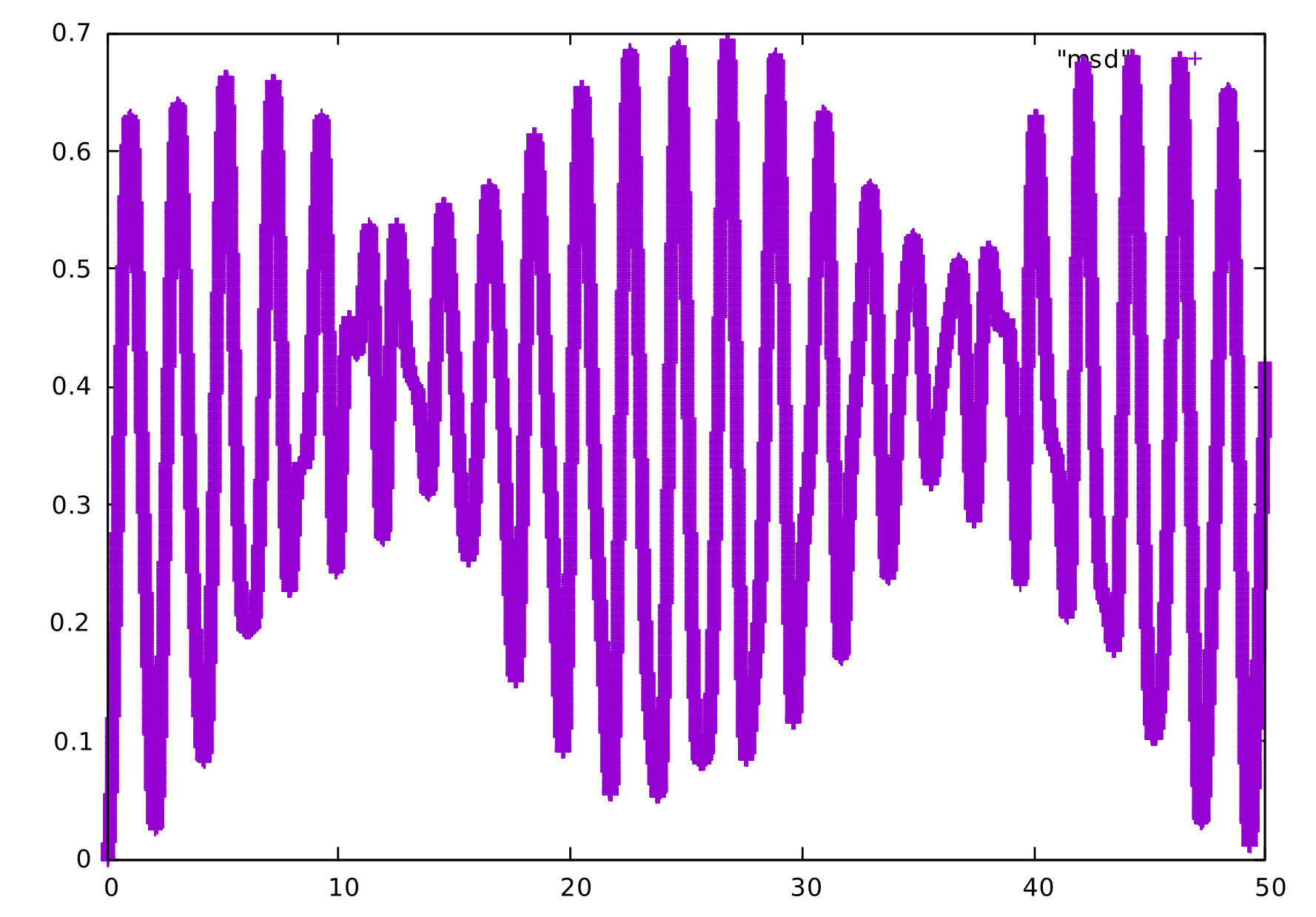
O desvio quadrático médio, mais conhecido na literatura como mean square displacement (msd), é dado por

$M(t)=\sum _{i=1}^{N}\vert \psi _{i}(t)\vert ^{2}(i-i_{0})^{2}$

e representa mais uma medida das propriedades espaciais das funções de onda. Nessas figuras aqui o msd é plotado como função do tempo para dois casos: campo $F=4$, $U_{1}=3$ e $U_{2}=0$ e campo $F=4$, $U_{1}=3$ e $U_{2}=3$. No primeiro caso notamos dois modos de oscilação, o primeiro sendo uma oscilação de alta frequência, que é modulada por uma oscilação de menor frequência, com uma média de 10 ou 15 oscilações de alta frequência para cada uma de baixa frequência. Quando o potencial $U_{2}$ passa de 0 para 3, nota-se que acompanhando cada oscilação de grande amplitude existem duas de amplitude menor, com duas de amplitude menor para cada oscilação de amplitude maior.

Gráfico 5: Mean Square Displacement como função do tempo para $F=4$, $U_{1}=3$ e $U_{2}=0$.

Gráfico 6: Mean Square Displacement como função do tempo para $F=4$, $U_{1}=3$ e $U_{2}=3$.

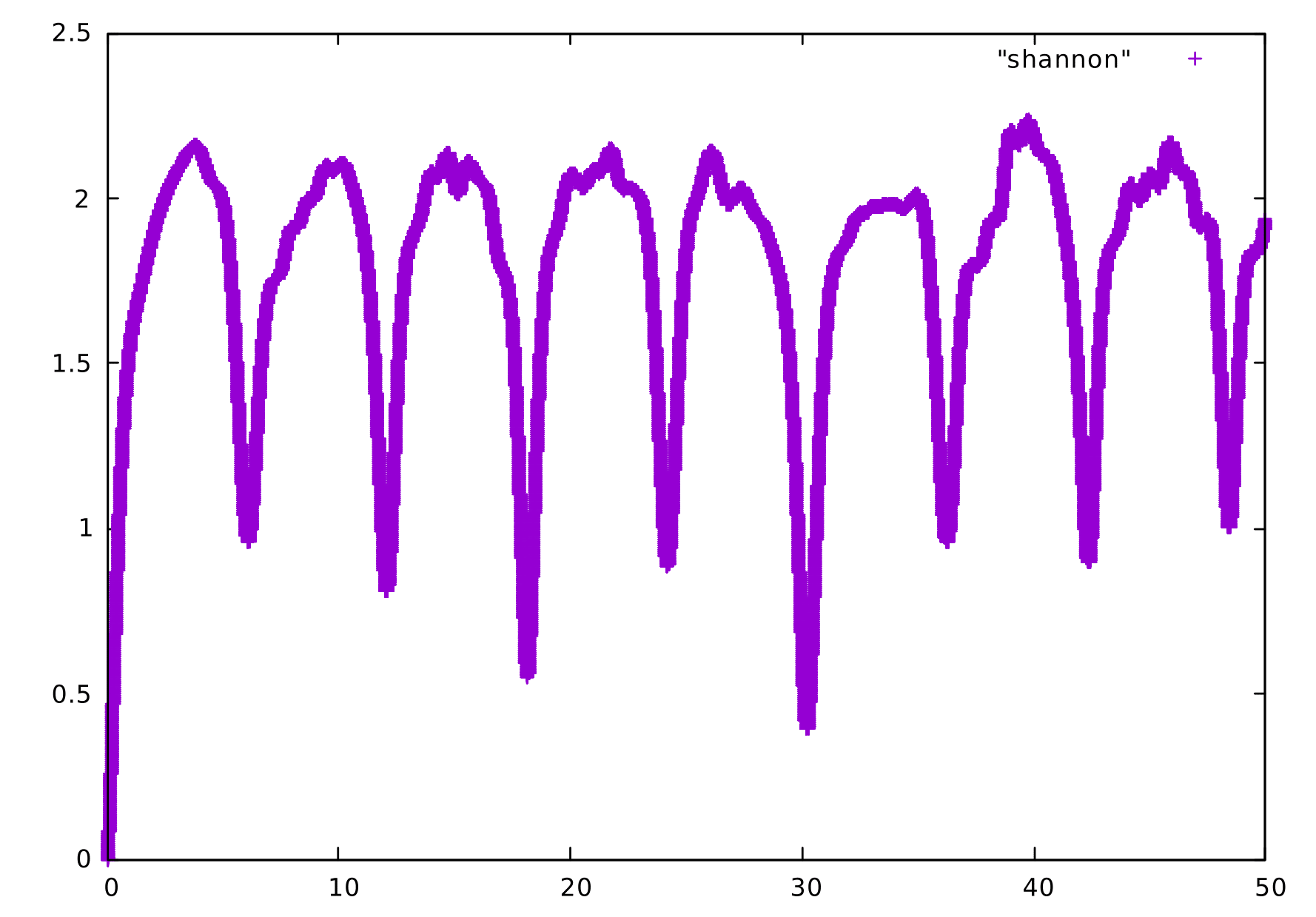
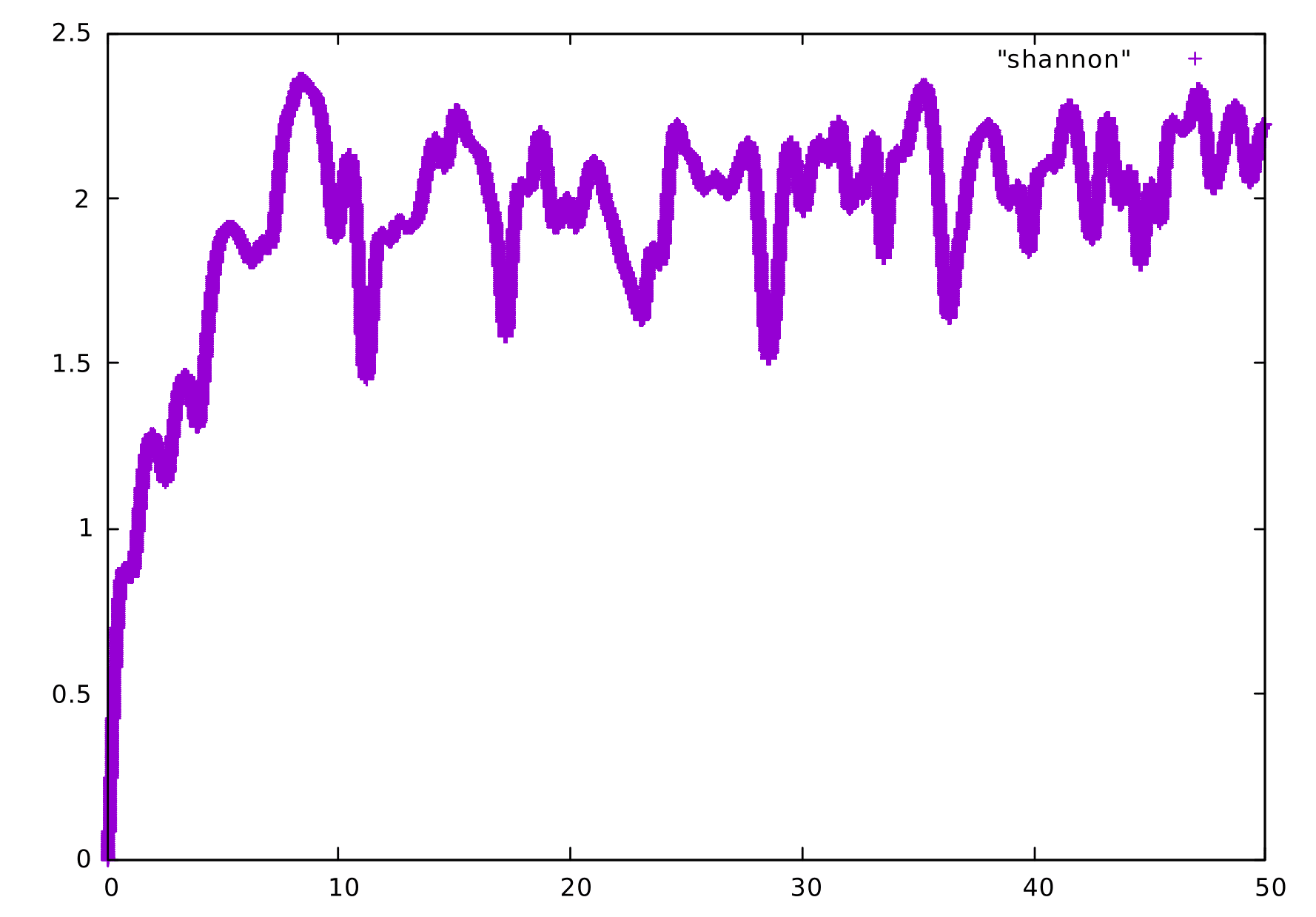
Outro parâmetro de interesse na integração destas equações acopladas é a entropia de Shannon, definida por

$S(t)=-\sum _{i=1}^{N}\vert \psi _{i}(t)\vert ^{2}ln\vert \psi _{i}(t)\vert ^{2}$

Grosso modo, ela pode ser interpretada como uma medida do grau de concentração espacial da probabilidade de encontrar a partícula na rede. Aqui são apresentadas duas imagens referentes a casos distintos: o primeiro é dado por campo $F=1$, $U_{1}=3$ e $U_{2}=0$, onde é possível notar que as oscilações de Bloch têm uma amplitude muito grande, e o segundo caso é referente a um campo $F=1$, $U_{1}=3$ e $U_{2}=3$. Para este último conjunto de valores dos parâmetros nota-se que as oscilações de Bloch possuem amplitude muito menor do que a do caso anterior, de forma que a entropia de Shannon apresenta alto grau de localização.

Gráfico 7: Entropia de Shannon como função do tempo para $F=1$, $U_{1}=3$ e $U_{2}=0$.

Gráfico 8: Entropia de Shannon como função do tempo para $F=1$, $U_{1}=3$ e $U_{2}=3$.

Bibliografia

[1] JUNGES, L. Dissertação de mestrado. IF-UFRGS, 2009. “A equação de Schrödinger não linear discreta com desordem de Aubry-André e com campo elétrico DC.”

[2] GARCIA, A. L. (2017) Numerical Methods for Physics

[3] COHEN-TANNOUDJI C., DIU B., LALOE F. Quantum mechanics. Volume 1. Wiley, 1991

[4] NEWMAN, M. (2013) Computational Physics