Grupo - Modelo Sznajd

De Física Computacional
Ir para navegação Ir para pesquisar

Introdução

O Modelo de Sznajd ou United we stand, divided we fall (USDF) é um modelo recente, proposto em 2000 para entender a dinâmica de opiniões através da física estatística. No ponto de vista de um físico, o comportamento de indivíduos a as interações entre eles constituem um nível microscópico de um sistema social. O modelo introduz o fenômeno chamado validação social:

Validação Social: Se duas pessoas compartilham da mesma opinião, os seus vizinhos começarão a concordar com elas.

Discordância Destrutiva: Se as pessoas discordam, os vizinhos começarão a argumentar com elas.

O método e Formulação Matemática

Opinião social é vinda de opiniões individuais, representadas neste modelo por spins de Ising de forma "yes" e "no". A dinâmica segue a relação da validação social:

  1. A cada timestep um par de sping Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i}, S_{i+1}} são escolhidos para tentar mudar os seus vizinhos mais próximos
  2. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i} = S_{i+1}} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i-1} = S_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i+2} = S_{i}} (validação social)
  3. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i} = -S_{i+1}} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i-1} = S_{i+1}} e

No modelo, dois tipos de estados estacionários são alcançáveis: consenso completo(ferromagnético) e impasse(antiferromagnético). A principal diferença para o Ising é que a informação flui para fora. O modelo de Sznajd ou USDF tem sido modificado e utilizado em marketing, política e finanças.

Modificações

Fala-se que o estado antes mencionado, o antiferromagnetismo, pode ser considerado não realístico para representar o comportamento de indivíduos em uma sociedade. Para tentar evitar este caso, propõe-se o seguinte:

  1. A cada timestep um par de sping são escolhidos para tentar mudar os seus vizinhos mais próximos igual anteriomente
  2. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i} = S_{i+1}} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i-1} = S_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i+2} = S_{i}} (validação social)
  3. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i} = -S_{i+1}} , então Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i-1} = S_{i}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{i+2} = S_{i}}

Estas regras ficaram conhecidas como algo do tipo: "Se você não sabe o que fazer, ou faz nada ou faz qualquer coisa." É um tanto quanto óbvio que o modelo unidimensional não representa bem um sistema social e que modelos bidimensionais são bem mais realistas. Algo interessante mencionar é a atualização simultânea para sistemas de duas dimensões: uma atualização simultânea leva a uma muito maior dificuldade de atingir o estado de consenso total. Isso foi mostrado por Stauffer[1] e a rezão para isso é que alguns recebem simultaneamente distintas informações de diferentes vizinhos, o que leva a não aceitar a opinião.

Regras para rede quadrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle LxL} :

  1. Se conjunto 2x2 de 4 vizinhos não tiverem todos os seus spins paralelos, deixam os seus oito vizinhos sem modificações
  2. Um par de vizinhos convence seus seis vizinhos a seguirem a sua orientação se o par de spins for paralelo.

A regra de atualização para duas dimensões pode ser obtida pela regra em uma dimensão: A regra e 1D é aplicada para cada uma das 4 cadeias de spins, como mostra a próxima figura: 1.jpg

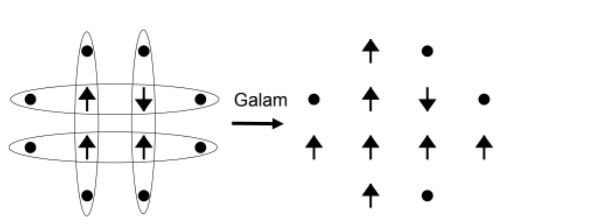
Isto foi mostrado por Gallam[2]

Generalização

Para a generalização desse método para a rede quadrada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} xFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} onde cada spin pode estar para cima ou para baixo e utiliza-se condições periódicas de contorno. A regra Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle II_{a}}

Aplicações

Como mencionado anteriormente, o modelo de Sznajd pode ser utilizado em política, marketing e finanças.

[3]

Bibliografia

  1. ↑ D. Stauffer D, J Math Sociol 28 25 (2004)
  2. ↑ S. Galam, J. Stat. Phys. 61, 943 (1990)
  3. ↑ D. Stauffer,A.O. Sousa,M. De Oliveira, Int. J. Mod. Phys. C 11 1239
Disponível em “http://fiscomp.if.ufrgs.br/index.php?title=Grupo_-_Modelo_Sznajd&oldid=2069”