Gnuplot
GNUPLOT é um programa para fazer gráficos de livre distribuição. Gnuplot é interativo, mas a comunicação é na linha de comando (sem menus nem uso do mouse). Pode se graficar funções em uma o duas variáveis (mapas de contorno também) definidas dentro dele ou de arquivos de dados externos. O link abaixo contem a documentação completa. Aqui apresentamos tutoriais baseados em exercícios simples.
- GNUPLOT documentation
Escreva "gnuplot" no seu terminal X (xterm), e verá algo assim na sua tela:
G N U P L O T
Version 4.0 patchlevel 0
last modified Thu Apr 15 14:44:22 CEST 2004
System: Linux 2.6.18-5-k7
Copyright (C) 1986 - 1993, 1998, 2004
Thomas Williams, Colin Kelley and many others
This is gnuplot version 4.0. Please refer to the documentation
for command syntax changes. The old syntax will be accepted
throughout the 4.0 series, but all save files use the new syntax.
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from
http://www.gnuplot.info/faq/
Send comments and requests for help to
<gnuplot-info@lists.sourceforge.net>
Send bugs, suggestions and mods to
<gnuplot-bugs@lists.sourceforge.net>
Terminal type set to 'x11'
Comandos básicos
Os seguintes exercícios visam a familiarização com o Gnuplot para depois poder fazer os gráficos do seu interesse.
Graficando funções:
- plot
Esse é o comando para desenhar gráficos 2D. Ele pode graficar ("plotar") a partir de uma função ou de dados lidos de um arquivo. Por exemplo, para graficar a função seno,
gnuplot> plot sin(x)
Para graficar a função cosseno no mesmo gráfico do seno, utiliza-se, em seguida,
gnuplot> replot cos(x)
Neste caso, se utilizássemos plot no lugar de replot, então o gráfico da função seno seria perdido.
- splot
Esse é o comando para desenhar gráficos 3D. Ele pode graficar ("plotar") a partir de uma função ou de dados lidos de um arquivo de maneira muito semelhante ao comando plot. Por exemplo:
gnuplot> splot x*y
Se quisermos graficar outra curva no mesmo gráfico, utiliza-se o replot em seguida da mesma maneira que em gráficos 2D:
gnuplot> replot x/y
- Nomear os eixos
gnuplot> set xlabel "eixo Y"
gnuplot> set ylabel "eixo X"
- Acrescentar o título "SENO e COSENO" e re-desenhar
gnuplot> set title "SENO e COSENO"
gnuplot> replot
Atenção: se o gráfico é para ser inserido num relatório, então não colocamos título
- Legendas: identificar as funções com os nomes "seno(x)" e "coseno(x)" respectivamente
gnuplot> plot sin(x) title "seno(x)", cos(x) title "coseno(x)"
- O gnuplot usa autoscale para dados e a escala x: -10, 10 para funções
Podemos alterar os intervalos assim (por exemplo x entre 0 e 5, y entre -3 e 3)
gnuplot> set xrange [0:5]
gnuplot> set yrange [-3:3]
- Ativar a grade
gnuplot> set grid
gnuplot> replot
- Desligar a grade
gnuplot> unset grid
gnuplot> replot
- Passar a coordenadas polares (atenção é uma representação x,y de um gráfico polar (theta,rho=f(theta))
gnuplot> set title "GRAFICO POLAR" ! trocar título
gnuplot> set polar
gnuplot> plot t
gnuplot> set trange [0:4*pi] ! mudamos o intervalo do t (variável de ângulo theta)
gnuplot> replot
gnuplot> set size square ! fazer o gráfico quadrado
gnuplot> replot
- Salvar a sessão num arquivo
gnuplot> save "test1.gnu" ! o .gnu é só por conveniência
- Sair do Gnuplot
gnuplot> quit
- Conferir se foi gravado (fora do Gnuplot, na tela de comandos) e recarregar depois
$ ls -l *.gnu
$ gnuplot ! para entrar de novo
gnuplot> load "test1.gnu"
gnuplot> replot
- Experimente mais (e interprete o resultado):
gnuplot> plot sin(t)
gnuplot> plot cos(t)
gnuplot> plot sin(t), cos(t)
gnuplot> plot sin(t)*cos(t)
gnuplot> quit
- Graficando dados
1. Crie um arquivo de dados (x,y) com a relacao y=x² entre -5 e 5 e 100 pontos (use 'seq' e 'awk')
2. Grafique os dados (ex: x2.dat) no gnuplot
$ gnuplot
gnuplot> plot "x2.dat"
- Graficando com linha em lugar de pontos
gnuplot> plot "x2.dat" with line ! o with line pode ser abreviado para w l
gnuplot> set style data linespoints ! isto deixa o estilo linha e pontos fixo
gnuplot> replot
- Mudando para linha sem pontos
gnuplot> set style data lines
gnuplot> replot
- Escala logarítmica (os dois eixos)
gnuplot> set log
gnuplot> replot
- Voltar a escala linear
gnuplot> unset log
- Trocar X com Y
gnuplot> plot "x2.dat" using 2:1 ! pode ser abreviado para u 2:1)
- Salvar eps colorido (imprimir ou incluir em LaTex)
gnuplot> set term postscript enhanced color !formato postscript colorido e de qualidade
gnuplot> set output "x2.eps"
gnuplot> replot
- Salvar eps em tons de cinza
gnuplot> set term postscript enhanced monochrome
gnuplot> set output "x2.eps"
gnuplot> replot
- Se queremos o gráfico para inserir num relatório, pode se perceber depois da primeira tentativa que as fontes,
--isto é números e textos que aparecem dentro do gráfico-- ficam muito pequenas no fim. Isto pode ser facilmente concertado com o seguinte truque. Antes de mudar o terminal e a saída, ou seja antes dos passos 20 ou 21, fazer:
gnuplot> set size 0.5
gnuplot> replot
Isso escala todo o gráfico num fator 1/2, mas mantendo o tamanho das fontes. O efeito no relatório será o de ver as fontes e símbolos aumentados num fator 2.
- Após produzir a saída postscript (eps) se quiseres voltar a usar o GNUPLOT normalmente faça
gnuplot> set output
gnuplot> set terminal x11
Ajuste de curvas (fit)
Definir uma função
gnuplot> f(x) = a + b*x
Utiliza-la para o ajuste dos dados
gnuplot> fit f(x) "x.dat" via a,b
Resultado:
...
After 6 iterations the fit converged.
final sum of squares of residuals : 3.76358e-28
rel. change during last iteration : 0
degrees of freedom (FIT_NDF) : 98
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.95969e-15
variance of residuals (reduced chisquare) = WSSR/ndf : 3.84039e-30
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 10 +/- 3.89e-16 (3.89e-15%)
b = -3 +/- 6.789e-17 (2.263e-15%)
correlation matrix of the fit parameters:
a b
a 1.000
b -0.864 1.000
Graficando dados e ajuste
gnuplot> plot "x.dat", f(x)
Outros comandos
- set key
Habilita legendas para as curvas do gráfico. Caso não seja utilizado, por default uma legenda será colocada no canto superior direito do gráfico. No caso de mais de uma curva, as legendas vão sendo colocadas abaixo das anteriores. Para desabilitar as legendas, basta um dos comandos (equivalentes):
gnuplot> set key off
gnuplot> unset key
gnuplot> set nokey
- set parametric
Coloca em modo paramétrico, ou seja, há uma função para cada eixo. Por exemplo, no caso de uma superfície o comando assume a forma:
gnuplot> splot x(u,v) y(u,v) z(u,v)
- set hidden3d
Faz com que as linhas 'de trás' de uma superfície não sejam plotadas. Assim, fica visível apenas a parte externa da figura.
gnuplot> set hidden3d
- set view
Controla o ângulo de visão (ou seja, como os eixos estão dispostas na tela) e a escala deles.
gnuplot> set view 30, 40, 2, 3
Nesse caso, 30 indica uma rotação de 30º em torno do eixo x; 40 indica uma rotação de 40º em torno do eixo z; 2 indica um aumento de 2 vezes na escala geral do gráfico; 3 indica um aumento de 3 vezes na escala do eixo z em relação à escala geral. No Gnuplot o eixo x é paralelo ao eixo horizontal do monitor, com sentido positivo para a direita; o eixo y é paralelo ao eixo vertical do monitor, com sentido positivo para cima; o eixo z é o eixo 'para fora' do monitor (regra da mão direita - sistema dextrogiro). Para ver isso, basta não fazer nenhuma rotação nos eixos, ou seja:
gnuplot> set view 0, 0
Caso o comando não seja utilizado, o valor estabelecido por default equivale a:
gnuplot> set view 60, 30, 1, 1
- set isosamples
Determina o número de isolinhas. Isolinhas são curvas parametrizadas geradas mantendo um dos parâmetros (u ou v) constante e variando o outro. São as curvas que compõe a malha da superfície. Mais curvas implica um gráfico mais preciso, porém que leva mais tempo para ser gerado. Exemplo:
gnuplot> set isosamples 60, 30
O valor default equivale a:
gnuplot> set isosamples 10, 10
- set xyplane
Ajusta a posição na qual o plano xy é desenhado num plot 3D. É útil, por exemplo, para o caso em que há uma projeção do gráfico do plano xy porque permite escolher em que 'altura' essa projeção será desenhada. É possível determinar o ajuste em termos absolutos ou relativos. No primeiro caso, temos:
gnuplot> set xyplane at 1
Nesse caso, o plano xy será desenhado em z=1. No segundo caso, temos (recomendado):
gnuplot> set xyplane relative 0.8
Nesse caso, a posição do plano xy é dada como uma fração da amplitude do eixo z. Um comando equivalente a este é:
gnuplot> set ticslevel 0.8
O valor default equivale a:
gnuplot> set xyplane relative 0.5
- set dummy
Por default, gnuplot assume que, para o comando plot, a variável independente é "x" e, em modo polar ou paramétrico, ela é "t". Para o comando splot, ele assume que as variáveis são "x" e "y" e, em modo paramétrico, "u" e "v" (não é possível utilizar modo polar com splot).
Pode ser conveniente alterar o nome de uma variável independente para uma letra convencional ou uma que possua um significado físico. Assim, para fazer "b" a variável independente num plot:
gnuplot> set dummy b
gnuplot> plot sin(b), cos(b)
Ou, num splot:
gnuplot> set dummy f,h
gnuplot> splot f*h
Exemplos
Script 01
set nokey
set parametric
set hidden3d
set view 65, 340
set isosamples 60, 40
splot [0:3*pi][-pi:pi] cos(u)*(u/(3*pi)*cos(v)+2), \
sin(u)*(u/(3*pi)*cos(v)+2), u*sin(v)/(3*pi)
pause -1
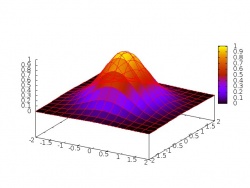
Script 02
set xrange [-2:2]
set yrange [-2:2]
set pm3d
set nokey
set isosamples 15,15
splot exp(-x*x)*exp(-y*y)
pause -1
Script 03
set xrange [-4:4]
set yrange [-4:4]
set pm3d at b
set xyplane relative 0.8
set isosamples 30,30
splot x*x*exp(-x*x)*y*y*exp(-y*y)
pause -1
Funções
| Função | Argumento | Retorno |
|---|---|---|
| abs(x) | qualquer | valor absoluto de x |
| abs(x) | complexo | módulo de x |
| acos(x) | qualquer | inversa do cosseno |
| acosh(x) | qualquer | inversa do cosseno hiperbólico |
| arg(x) | complexo | fase (ou argumento) de x |
| asin(x) | qualquer | inversa do seno |
| asinh(x) | qualquer | inversa do seno hiperbólico |
| atan(x) | qualquer | inversa da tangente |
| atan2(y,x) | inteiro ou real | inversa da tangente, tan−1 (y/x) |
| atanh(x) | qualquer | inversa da tangente hiperbólica |
| EllipticK(k) | k ∈ (-1:1) real | integral elíptica completa K(k) de primeiro tipo |
| EllipticE(k) | k ∈ [-1:1] real | integral elíptica completa E(k) de segundo tipo |
| EllipticPi(n,k) | n<1 real, k ∈ (-1:1) real | integral elíptica completa Π(n, k) de terceiro tipo |
| besj0(x) | inteiro ou real | função de Bessel j0 |
| besj1(x) | inteiro ou real | função de Bessel j1 |
| besy0(x) | inteiro ou real | função de Bessel y0 |
| besy1(x) | inteiro ou real | função de Bessel y1 |
| ceil(x) | qualquer | menor integral, não menor do que x (parte real) |
| cos(x) | qualquer | cos(x) |
| cosh(x) | qualquer | cosseno hiperbólico de x |
| erf(x) | qualquer | função erro de real(x) |
| erfc(x) | qualquer | 1.0 - função erro de real(x) |
| exp(x) | qualquer | função exponencial de x |
| floor(x) | qualquer | maior integral, não maior que x (parte real) |
| gamma(x) | qualquer | função gamma de real(x) |
| ibeta(p,q,x) | qualquer | função ibeta de real(p,q,x), ibeta(real(p,q,x)) |
| inverf(x) | qualquer | inversa da função erro de real(x) |
| igamma(a,x) | qualquer | função igamma de real(x), igamma(real(a,x)) |
| imag(x) | complexo | parte imaginária de x como um número real |
| invnorm(x) | qualquer | inversa de norm(x) |
| int(x) | real | parte inteira de x, truncada para zero |
| lambertw(x) | real | função Lambert W |
| lgamma(x) | qualquer | função lgamma de real(x), lgamma(real(x)) |
| log(x) | qualquer | logaritmo natural de x |
| log10(x) | qualquer | logaritmo (base 10) de x |
| norm(x) | qualquer | função da distribuição normal (Gaussiana) de real(x) |
| rand(x) | qualquer | gerador pseudo-randômico de números |
| real(x) | qualquer | parte real de x |
| sgn(x) | qualquer | 1 se x>0, -1 se x<0, 0 se x=0. imag(x) ignorada |
| sin(x) | qualquer | seno de x |
| sinh(x) | qualquer | seno hiperbólico de x |
| sqrt(x) | qualquer | raiz quadrada de x |
| tan(x) | qualquer | tangente de x |
| tanh(x) | qualquer | tangente hiperbólica de x |