Derivada Numérica

A derivada numérica permite estimar a derivada de uma função matemática usando os valores da função.

O método numérico se baseia na própria definição de derivada: o limite do quociente incremental da função quando o incremento tende a zero. Matematicamente é mais claro:

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

Se nessa expressão não tomamos o limite podemos obter uma estimativa numérica da derivada que dependerá do valor do incremento $h$:

$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}$

A expressão a direita é chamada de quociente diferencial de Newton.

Ao usá-la para calcular a derivada numericamente devemos ser cientes de que não é um cálculo exato. Existem duas fontes de erro nessa expressão, o erro de truncamento e o erro de arredondamento. Para estimar o erro de truncamento recorremos a Formula de Taylor:

$f(x+h)=f(x)+f^{\prime }(x)h+\frac{1}{2}{f}^{″}(x)h^2+\frac{1}{6}{f}^{‴}(x)h^3+...$

Por tanto:

$\frac{f(x+h)-f(x)}{h}=f^{\prime }+\frac{1}{2}{f}^{″}h+...$

Se o $h$ for pequeno podemos dizer que o erro ao usar a quociente de Newton para calcular a derivada é proporcional a $h$. De maneira geral o erro cresce linearmente com $h$. Por tanto devemos usar valores pequenos do incremento. No entanto ao fazer a conta numérica temos precisão finita (o numero de casas dos números). Não é possível levar a expressão ao limite teórico $h\to 0$. Então pelo outro extremo aparece o segundo tipo de erro, o de arredondamento. Quando $h$ é muito pequeno, ao fazer a diferença ente os dois valores da função, podemos ter esse erro que vai ser relativamente maior quanto menor for $h$, piorando a estimativa da derivada. Isso coloca um limite inferior para o incremento $h$ e assim para a precisão da estimativa numérica da derivada.
Resumindo, por um lado temos o erro de truncamento e pelo outro o de arredondamento, a valor ótimo será uma solução de compromisso entre os dois tipos de erro.

Outro cálculo numérico da derivada pode ser feito baseado na declividade de dois pontos próximos, um antes e outro depois do ponto onde queremos avaliar a derivada: (x-h,f(x-h)) e (x+h,f(x+h)).
A declividade da linha definida por esses dois pontos é;

$\frac{f(x+h)-f(x-h)}{2h}$

que é chamada de derivada centrada.
O erro desta estimativa é menor que na estimativa para frente (ou para atrás).

Existem formas de contornar o problema do valor ótimo de incremento podendo ir a valores menores dele e sim melhorar a estimativa da derivada numérica.

Programa

Implementar a derivada numérica em FORTRAN é apenas uma linha de código:

...
Df = (f(x+h) - f(x))/h
...

Onde f(x) deve ser definida num bloco FUNCTION F(x) ... END FUNCTION F.
O resto depende de onde e para que queremos calcular a derivada.

Exemplos

Com a função f(x) abaixo, a modo de exemplo, a questão do compromisso entre o erro de truncamento e o erro de arredondamento deve-se esclarecer.
A função é:

$f(x)=\frac{\sin (x^2)e^{x/3}}{\sqrt{x^2+4}}$

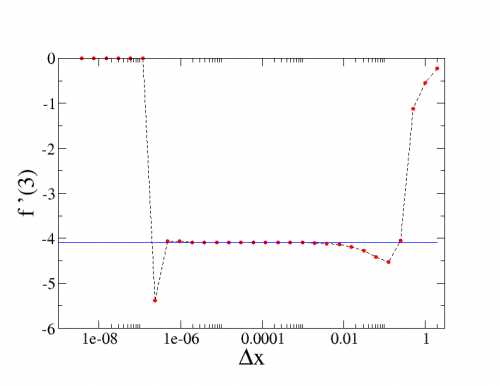
Com o método descrito acima vamos avaliar numericamente (para frente) a derivada num ponto qualquer, digamos x=3. A continuação figuras mostrando o resultado para vários valores de $\mathrm{\Delta }X$ decrescentes num fator 2 partindo de 2. Ou seja $\mathrm{\Delta }X=${2, 1, 1/2, 1/4, ...}

A esquerda a derivada em x=3 numérica em função do $\mathrm{\Delta }x$ utilizado. O valor exato da derivada em é $f^{\prime }(3)=-4.08963$
Vemos que em volta de $\mathrm{\Delta }x=0.01$ começa a convergir, piorando a partir de $\mathrm{\Delta }x=10^{-6}$.
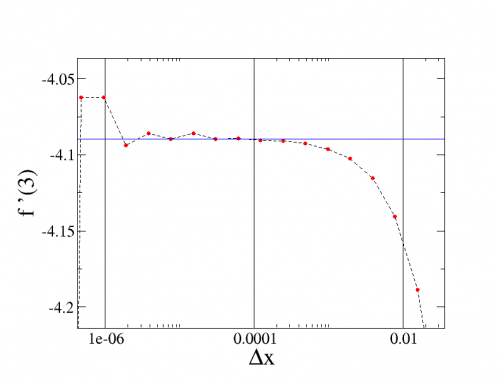
Na figura a direita vemos ampliada a região de convergência, onde o valor de $\mathrm{\Delta }x=8x10^{-5}$ parece ser o ótimo.
NOTA: os programa FORTRAN usado para o calculo da derivada esta em Real (ou Real*4, ou seja ponto flutuante em representação de 32 bits).
Como seria em dupla precisão (Real*8)?

Links Externos

• Numerical Differentiation Quant Equation Archive, sitmo
• http://mathworld.wolfram.com/NumericalDifferentiation.html
• http://math.fullerton.edu/mathews/n2003/NumericalDiffMod.html